单站无源定位系统对消电路设计

赵岩

（中国西南电子技术研究所四川成都610036）

单站无源定位系统对消电路设计

赵岩

（中国西南电子技术研究所四川成都610036）

针对单站无源定位系统中侦收通道内直达波干扰信号的影响问题，设计了一种自适应对消电路方案。通过对对消电路的数学模型进行分析结合仿真验证，提出一种相位、幅度分步骤调节的实现方案。该方案控制逻辑简单、电路易于实现，并进行了电路实际测试。测试结果表明，电路可实现31 dB的对消比。

无源定位；射频对消；自适应；对消比

无源相干定位PCL（Passive Coherent Location）系统，其本身不辐射电磁波，而是利用外部已知信号作为辐射源，如广播电台、电视台等信号对飞机、导弹等空中机动目标进行探测[1]。由于其自身不主动辐射电磁波，其隐身性较好[2-4]，战场生存能力强。另外，由于其无需发射装置，所以系统体积小、成本相对较低[5]。此外，由于其定位所采用的辐射源具有频率低的特点，其对隐身目标具有很好的探测效果[6]。

对于利用调频广播信号的无源相干定位系统，由于广播信号多使用全向天线，接收机接收的目标回波信号远小于直达波干扰信号[7-8]，这对数据处理部分的ADC芯片动态范围指标压力很大。因此，需要设计相应的对消电路削弱直达波干扰信号，进而降低ADC芯片的动态范围指标要求，减小数据处理压力[9]。

1 对消电路数学原理分析

理想情况下的对消是通过对消电路产生和干扰信号幅度相同、相位相反的对消信号，并将其与干扰信号矢量相加，达到消除干扰的目的。实际情况下，对消电路产生的对消信号同理想对消信号之间存在一定的幅度差和相位差。如图1所示。

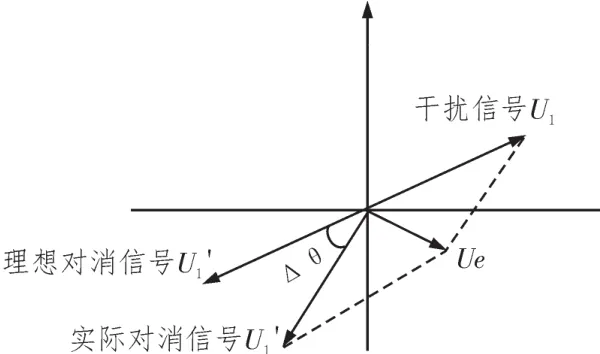
图1 对消矢量图

在实际电路中，假设干扰信号U1，实际对消信号为同理想的对消信号的误差相位为Δθ，因此其不能完全消除干扰信号，与干扰信号会产生一个对消剩余矢量Ue，评价对消电路对消效果的指标为对消比，dB形式的对消比公式为:

根据图1所示，可以得出Ue同的关系为:

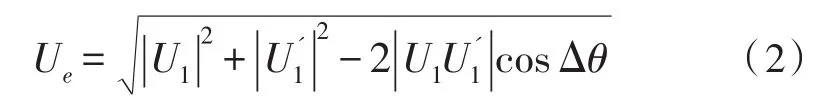
将式（2）带入式（1），则对消比和对消信号和误差相位之间的数学关系如下式:

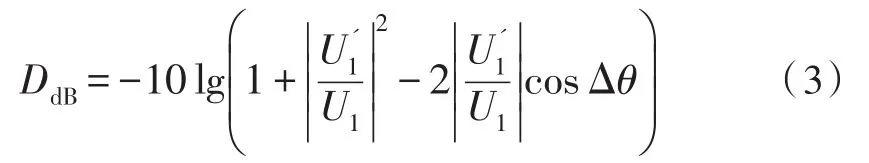
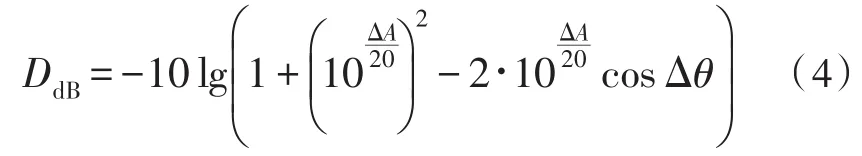
由式（4）得出对消比同幅度误差ΔA及相位误差Δθ之间的关系，如图2所示。

图2 幅度误差、相位误差与对消比之间关系

因此，从上图可以看出，对消比受相位误差与幅度误差综合因素影响。根据式（4）计算，若要达到30 dB的对消比，当幅度一致时，即ΔA=0时，相位误差要控制在以内。当相位一致时，即Δθ=0时，幅度误差要控制在±0.4 dB之内。实际电路设计中，无论是幅度或者相位都无法做到误差为0，因此实际的对消比要根据器件的准确度进行具体仿真计算。

2 对消方案对比

基本的开环对消电路思路很简单，先测得侦收通道干扰信号和参考通道的直达波信号之间的幅度差和相位差，根据测试结果，选定衰减器和移相器的衰减值和移相值，再将调节后的信号通过合成器与侦收通道的干扰信号进行合成，达到对消的目的。由于此对消电路不具备自适应调节功能，不利于多站批量生产装配。且即使在同一定位站，受天气因素等外部环境的影响，到达对消电路侦收通道和参考通道的信号幅度和相位差都会有一定的波动，因此多应用于直达波干扰路径且不受外部环境影响的主动雷达系统[10]。

在单站无源定位系统中，一般采用闭环自适应对消系统，一种典型的自适应对消电路如图所示[11]。

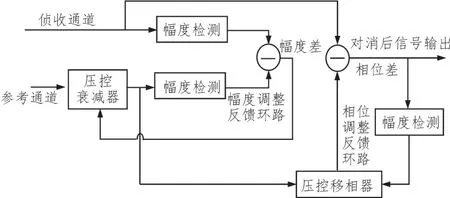
图3 一种自适应对消电路

这种对消电路包含两个自适应对消环路。一个是幅度对消环，一个是相位对消环。由于在调节压控衰减器及压控移相器过程中，信号的相位、幅度信息还会产生变化，因此对消环路要经过多个递归过程，才能达到对消比要求。图3中的对消电路是纯模拟电路的对消电路，随着软件无线电技术、DSP、FPGA技术的发展，数字处理芯片被引入到对消电路中，可以采用数字-模拟结合的方式[12]，或纯数字的方式[13]达到更加好的对消效果，也减小了设备体积，但是由于DSP、FPGA等器件的引入，提高了对消设备的成本。

通过对式（4）分别对Δθ及ΔA求偏导，得

令式（5）为0，可知，对消比D在 Δθ位于[0，360）区间内内有且仅有一个极值点，即当Δθ=0时，D处于极值，与无ΔA关。令式（6）为0，可知，对消比D在 ΔA=20lg(cosΔθ)时，处于极值点，但是当 Δθ位于[180，360）区间内时，ΔA=20lg(cosΔθ)为负值。但是无源定位体制中，由于系统设计上均认为参考通道的直达波信号大于侦收通道的干扰信号，故ΔA肯定为大于0的某值，即此时无论如何调节ΔA，均无法达到对消比D的极值点。通过上述分析可以得出如下结论:在对消电路中，无论初始相位差值和幅度差值是多少，在[0，360）区间内调节移相器，总会找到一个最佳的Δθ，此时对消比最大。但当初始相位差Δθ不确定的前提下，调节数控衰减器，不一定能找到对消比最大的衰减值，仅当Δθ位于[0，180]区间内时，调节数控衰减器可以找打对消比最大的点。应此，在实际设计电路过程中，根据上述分析结论，在对消电路调节过程中，应先调节数控移相器，再调节数控衰减器。

3 电路设计

通过上述分析可知，为提高对消电路的对消能力，对幅度和相位的控制调节应当按一定的顺序进行，否则在某些初始相位差条件下，可能导致对消失败。基于此，提出一种控制逻辑简单、不需要DSP、FPGA等芯片的对消电路，如图4所示。在对消的过程中，通过判断对消比的变化趋势，检测对消后输出信号幅度，找到对消比极值点的方法，按照首先调节对消信号和干扰信号相位差，然后再来调节对消信号的幅度差的方式，最终达到对消的目的。

图4 对消方案框图

如图4所示，参考通道的信号，经过数控衰减器和数控移相器后，同侦收通道的信号通过合成器进行合成。合成后的信号经过包络检波器后输出，记包络检波器输出为A路，对A路的电压信号经AD采样采集信号的电压信息，此电压信息的大小直接反应对消比的大小，电压越小，说明输出信号功率越小，对消比越大。再经过单片机简单的判断比较，根据一定的控制逻辑对数控衰减器和数控移相器进行控制。

A路电压信号的数据处理过程如下:

1）初始状态下数控衰减器的衰减值设为0 dB，数控移相器的移相值设为0°。采集A路信号的电压信息，作为电压初值。

2）调节数控移相器，按移相器最小步进增加移相值，调节数控移相器从0°到360°变化，在调节过程中，采集并记录A路信号的输出电压值。遍历调节完成后，将移相器的移相值调节至A路输出电压值最小的位置。

3）调节数控衰减器，从0 dB开始依衰减步进增加，在增加过程中采集并记录A路信号的输出电压值。遍历调节完成后，将衰减器的衰减值调节至A路输出电压值最小的位置。

经过上述调节后，对消比应当已经达到极值点。但是实际电路中，根据移相器和衰减器的实现原理[14-15]，在移相器、衰减器调节过程中会引入损耗及相位的变化，应进行修正。

4）在当前移相值和衰减值处，按最小步进增大和减小衰减值，取A路电压值最小值固定移相值和衰减值此时对消完成，达到最佳对消效果。

4 仿真分析

结合目前数控衰减器及数控移相器器件能力，比较常见的30 dB动态范围的数控衰减器的最小步进为0.5 dB，8位数控移相器移相精度为1.4°。根据这些器件实际情况，并随机设置参考通道输入信号为0 dBm，侦收通道信号为-20 dbm。两路信号初始相位差为143.5°建立仿真模型。通过ADS软件的tune调谐功能，按照上文分析的对消调节步骤移相器和衰减器进行控制。对消结果仿真如下图所示，可以看出，最终对消比为45.9。由仿真结果可以看出，按照本方案设计，选用目前常见器件，可以达到30 dB以上对消比。

5 实际电路测试

根据上述分析及仿真结果，设计加工对消电路。电路由数控移相器、数控衰减器、单片机、检波器、合成器等主要器件构成，制成后的对消电路单元大小为19寸1U标准插箱。电路上电后，自动开始对消过程，可通过CAN总线对对消状态进行实施监控。实际电路测试结果如下。

6 结束语

单站无源定位技术具有巨大的应用前景，而与之相应的对消技术的发展对其影响巨大。本文从对消电路的基本数学原理入手，提出了相位、幅度分步骤调节的对消电路实现方式。通过电路实际测试，验证了方案的正确性，为对消电路的实现方式，提供了一种自适应、易实现、低成本的解决方案。

图5 分步调节对消比仿真结果对消比

图6 对消前、后干扰信号和回波信号对比

[1]蓝红生，古军峰，王国恩.单站无源定位技术研究[J].舰船电子工程，2014，34（5）:56-58，61.

[2]郑灿，李子杰，王旭赢.基于调频广播无源定位的有效可定位区[J].电子信息对抗技术，2011，26（6）:13-17.

[3]杨弘，韩令军.无源定位对机动目标跟踪研究[J].中国新通信，2011，18（8）:74-79.

[4]王正生，仇雅芳，王琳，等.卡尔曼滤波算法在单站无源定位中的应用[J].舰船电子对抗，2014，37（5）:27-30.

[5]徐锐.基于相位干涉仪体制的单站无源定位系统研究[D].成都:电子科技大学，2011.

[6]许德刚.基于调频广播的外辐射源雷达抗干扰技术[J].无线电工程，2015，45（4）:36-39，76.

[7]高宪军.单站无源定位的一种改进的粒子滤波算法[J].电子设计工程，2016，24（5）:107-109.

[8]刘芳，李会勇，张青松.一种模数结合的闭环迭代旁瓣对消方法[J].现代雷达，2014，36（11）:76-79，91.

[9]LU Xiao-de，YANG Peng-cheng，LI Dao-jing.et al.Interference cancellation based on compressive sensing for Passive coherent Radar（PACOR）[C]//Radar Conference，2015，proceeding of 2015 IEEE.IEEE，2015:0527-0532.

[10]李成虎.毫米波FMCW雷达中射频对消技术研究[D].成都:电子科技大学，2012.

[11]杨天虹，屈乐乐，邵清亮，等.连续波雷达同频干扰微波对消技术研究[J].微波学报，2011，27（6）:32-36.

[12]刘芳，李会勇，张青松.一种模数结合的闭环迭代旁瓣对消方法[J].现代雷达，2014，36（11）:76-79，91.

[13]马晓静，刘育才.自适应旁瓣对消技术及其在数字阵列雷达中的应用[J].雷达与对抗，2010，30（3）:25-29.

[14]谢萍，邓军，田小建.C波段反射型线性360°模拟移相器的设计[J].吉林大学学报，2013（2）:131-136.

[15]杨晓明，白海蛟.Ku波段温补电调衰减器设计[J].制导与引信，2011，32（3）:57-60.

[16]刘建成，全厚德，袁丁，等.衰减器误差对射频干扰对消系统的影响[J].指挥与控制学报，2015，1（4）:470-475.

Cancellation circuit design of single station passive location system

ZHAO Yan
（Southwest China Institute of Electronic Technology，Chengdu610036，China）

In order to suppress the direct path interference of surveillance channel on passive radar，an automatic self-adaptive cancellation solution circuit is brought forward.Base on the mathematical models and result of simulation，phase and amplitude should adjust in steps.The control logic is simple and the circuit is easy to realize.Measurement results show that the actual circuit can achieve 31 dB cancellation ratio.

passive locating；RF cancellation；self-adaptive；cancellation ratio

TN952

B

1674-6236（2017）23-0151-04

2016-10-17稿件编号：201610084

赵岩（1988—），男，辽宁新民人，硕士，工程师。研究方向：射频微波电路。