初中数学函数概念起始课的有效教学案例研究

曹小红

【摘要】 对于初中生数学学科学习来讲，函数一直属于重点难点.他通过定义的变量来揭示现实生活中各种数量关系的变化和实质，属于学生理解现实生活和变化世界中数量关系的重要媒介.因此，为了让学生更好地将数学知识与生活联系起来，就必须加强对函数教学的重视程度.本文通过简要阐述初中数学函数起始课开展的时效性，并结合相应的函数起始课生活情境引入案例，进行初中数学函数概念起始课的有效教学案例研究，以期对我国未来初中数学函数教学提供參考依据.

【关键词】 初中数学教学;函数概念;起始课;教学案例

【基金项目】 此文为“人教版章节起始课的教学策略研究”课题研究成果之一，课题编号C2016183.

函数在初中教学阶段占有十分重要的地位，其包含着与各种数学思维和解题方法之间的关联性，因此，对初中生整体数学学习效果有着极大的影响.起始课指的是一门课程起首的那一堂课，也就是这门课的学习起点，主要以介绍该课程概况为主.据调查结果显示，我国当前初中数学函数概念起始课的教学质量参差不齐，因此，需要结合相应的有效教学案例进行分析，致力于提高我国初中数学函数概念教学的整体水平.

一、初中函数部分所占比例

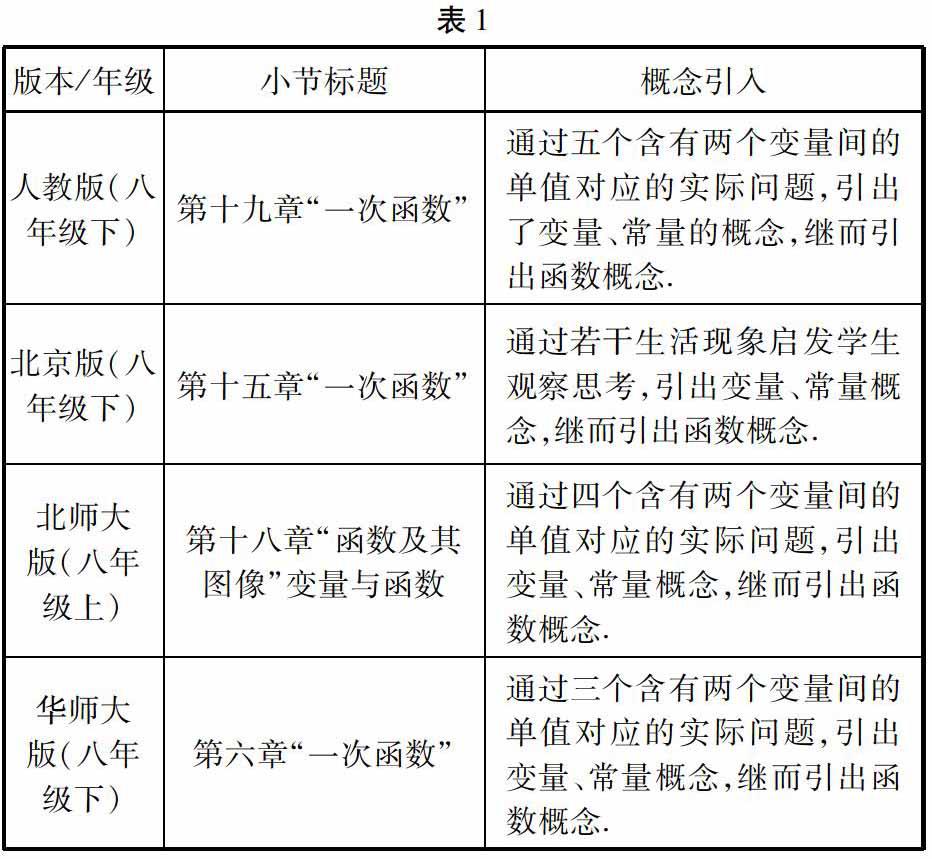
根据对人教版、北京版、北师大版以及华师大版本的初中数学教材进行调查研究，关于函数概念章节均是通过变量的定义来进行引入，具体见表1.

相对其他表达方式，变量法是最易被初中生所接受的方式，但也存在一些不足之处，比如，在对变量和常量进行描述时没有具体的界定，导致极易出现理解差错和歧义的状况.实际上，由于初中生的年龄和性格特点，以及函数概念的抽象性，极大地增加了初中数学函数概念的教学难度，因此，加强对此类问题的重视度十分必要.接下来，将以人教版为例对初中数学函数概念起始课教学展开探讨.

二、初中数学函数概念起始课开展的有效性

初中数学函数概念起始课一般是指在章节开头展开对后面要说的内容做一个大纲的阐述，使学习的人心里对函数概念有一个大概的认知，而结尾再对中间所讲述的内容做一个总结和拓展，深化初中生对函数概念的理解和掌握[1].由人教版八年级下册第十九章“一次函数”对函数概念的定义来讲，函数就是用符号来表示现实生活中的对应关系，并通过相应的运算和步骤来解决现实问题.而函数概念起始课，就是将此过程简单化、具体化的重要媒介，通过间接的方式表达相应运算，增添初中生对其理解程度的同时，也在一定程度上提高初中生的学习积极性与主动性.

三、初中数学函数概念起始课教学的案例分析

（一）生活情境引入

无论是初中数学学习还是其他学科的学习，都是为了培养学生逻辑思维和学习能力来解决现实生活中的问题.因此，在进行函数概念教学时应注重引入贴近生活的例子来进行解析，比如，

人教版初中数学第十九章“一次函数”章节，问题2：某登山队大本营所在地的气温为5摄氏度，海拔每升高1 km气温就下降6摄氏度.登山队员由大本营向上登高x km时，他们所在位置的气温是y摄氏度.使用函数解析式表示y与x之间的关系.

分析：y随x变化的规律是：从大本营向上，当海拔增加x km时，气温从5摄氏度减少6x摄氏度，因此，y与x的函数解析式为：y=5-6x.这个函数解析式也可以写为：y=-6x+5.当登山队员由大本营向上登高0.5 km时，它们所在位置的气温就是当x=0.5时，函数y=-6x+5的值，即y=-6×0.5+5=2（摄氏度）.

教师可根据这一情境引入，或者是增添其他情境，比如，天气变化、路程变化等，来引导初中生理解和掌握一次函数中变量和常量之间的相关关系，并延伸到函数概念中去，更好地进行初中数学函数概念教学.

（二）化繁为简进行练习

初中数学函数概念起始课的关键所在就是将复杂、抽象的问题简洁化，用通俗易懂的形式来将函数的变量与常量之间的对应关系表示出来.比如，

人教版初中数学第十九章“一次函数”章节19.1.1变量与函数，先请思考下面几个问题：汽车以60 km/h的速度匀速行驶，行驶路程为s km，行驶时间为t h，填写表2.s的值是随t值的变化而变化吗？

这些问题反映了不同时间的变化过程，其中有些量的数值是变化的，例如，时间t，路程s.但有些数是始终不变的，例如，速度60 km/h.在一个变化过程中，我们称发生变化的数值为变量，始终不变的数值为常量.

函数与方程不等式之间的关系可以通过图像来进行表达，将函数、不等式、方程三者相互连接，便于初中生加强理解.比如，

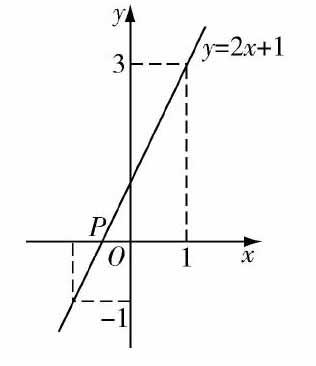
人教版初中数学第十九章“一次函数”章节19.2.3一次函数与方程、不等式，通过要求学生对2x+1=3;2x+1=0;2x+1=-1这三个方程进行比较，并给出如图所示，辅助理解.可以看出这三个方程等号左边都是2x+1，等号右边分别是3，0，-1.从函数的角度看，解这三个方程相当于在一次函数y=2x+1的函数值分别为3，0，-1时，求得自变量x的值.或者说在直线y=2x+1上去纵坐标分别为3，2，-1的点，看他们对应的横坐标分别为多少.因为任何一个x为未知数的一元一次方程都可以变形为ax+b=0（a≠0）的形式，所以解一元一次方程相当于某个一次函数y=ax+b的函数值为0时，求自变量x的值.

四、初中数学函数概念起始课教学的问题与分析

（一）“掐头”方式的合理性探讨

“掐头”方式是指教师并未过多的解释变量与常量之间的概念与区别，而是将重点放在函数关系上，尤其是在选取具有代表性的函数原型问题上.从时间角度上来讲，这种教学方式虽然具有较高的教学效率，但对学生思维逻辑长期培养方面来看具有一定的不利影响[2].因此，初中数学函数概念起始课教学应该注重整体性，不仅使学生了解简单的变量与常量之间的关系，还加深其对特殊值之间的对应关系的理解，突出单值对应.

（二）数学模型的有效选取

在对数学模型进行选取时，除了要注意其是否有效，还应加强对本质的突出表现. 在人教版教材中常常采取的数学

模型有“气温T与时间t”“路程s与时间t”等，从不同角度且贴近学生生活的进行情境创设，使学生更易将抽象的函数关系进行理解.

（三）数学模型的有效利用

在选取有效适合的数学模型后，就该考虑如何有效利用这一模型问题.模型概念教学主要分为三个阶段，包括引入、建立和巩固这三个部分.在此教学过程中，应当充分利用各情境的灵活性[3].比如，在处理气温T与时间t的关系时，可以反过来看时间与气温的关系，不仅能够全方位的促进学生对概念的理解，还节约了教师大量课时准备时间.

五、结束语

综上所述，函数的改变原本就是抽象难以理解的，再加上初中生对数学的接触仍处于起步阶段，所以具有更高的难度.因此，应注重寻求起始课这种简单易懂的教学方式来进行初中生数学函数概念教学.在进行函数概念讲解时，应适当增添知识点与实际案例的相互结合，将抽象的函数概念与初中生日常生活结合起来，在加强处总数学函数概念教学效果的同时，增添初中生学以致用的能力，为日后的数学学科学习打好坚实的基础.

【参考文献】

[1]李庾南，刘东升.藤蔓之美：从数式方程走向变量函数——以八年级“函数（第1课时）”教学为例[J].数学通报，2015（2）：40-42，57.

[2]伍春兰.初中函数概念起始课有效教学的案例分析[J].北京教育学院学报（自然科学版），2012（4）：42-45.

[3]周礼平.初高中函数概念衔接教学研究[D]：苏州大学，2011.