基于LSSVM-ARMA的电站锅炉NOx排放量动态软测量的研究

袁 洪， 宋选锋， 赵 征

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

基于LSSVM-ARMA的电站锅炉NOx排放量动态软测量的研究

袁 洪， 宋选锋， 赵 征

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

建立准确的 NOx排放量模型是锅炉优化降低NOx的基础。为提高NOx排放量的预测精度，提出基于最小二乘支持向量机和自回归滑动平均模型的锅炉 NOx排放量动态软测量的方法。基于某电厂330 MW机组的一段历史运行数据，首先，建立最小二乘支持向量机的NOx排放量静态软测量模型。其次，利用自回归—滑动平均方法实现对静态模型的动态校正。最后，针对2组不同样本验证LSSVM-ARMA模型和LS-SVM模型，得到2个模型的平均误差和均方根误差。结果表明：与LS-SVM 模型相比，LS-SVM与ARMA相结合的模型具有更高的预测精度，对于电站锅炉 NOx排放量的预测具有一定的有效性。

动态软测量； 最小二乘支持向量机； 自回归滑动平均； 氮氧化物排放量

0 引言

我国发电行业以燃煤锅炉为主，煤炭燃烧过程中产生的NOx是造成大气污染的主要因素。由于各种因素的制约，煤炭作为主要发电能源的事实近期很难改变。目前，对于电站锅炉NOx排放量的软测量方法可分为2种：静态建模和动态建模。实际运行中由于锅炉长期处于变工况的动态过程中，静态建模方法无法准确预测NOx的排放量。因此，研究火电机组NOx的动态软测量方法对于及时指导脱硝系统动作、实现节能减排都具有现实意义[1]。

文献[2]提出了基于锅炉燃烧模型的脱硝NOx软测量方法，采用软测量和多变量技术相结合的方法使脱硝控制优化达到了预期目标。文献[3]利用改进的广义动态模糊神经网络对电站锅炉燃烧过程建模，通过对比测试样本的NOx输出值和实际输出值验证了其性能的优越性。文献[4]建立了NOx排放量的前馈反向人工神经网络模型，并用实际值对其预测值进行了验证，证明了模型的有效性。这几种方法存在泛化能力差的问题。

由于最小二乘支持向量机建模具有较好的泛化能力，采用ARMA模型拟合时间序列可以得到当前时刻输出值与前几时刻系统输出变化之间的关系[5]。提出最小二乘支持向量机(Least Square Support Vector Machine，LS-SVM)与自回归滑动平均模型(Auto Regressive Moving Average，ARMA)相结合的方法建立NOx排放量的动态软测量模型，基于LS-SVM建立NOx排放的静态模型，将静态模型输出值与实际测量值比较得出一组时间偏差序列，然后用ARMA对时间偏差序列建模，从而实现静态模型的动态校正。该方法结构简单易实现，更加适用于实际生产。

1 最小二乘支持向量机

LS-SVM是将标准SVM采用最小二乘配方扩展形成的，最早是在1999年由Suykens和Vandewalle提出用于处理分类问题。LS-SVM采用误差平方损失函数通过二次规划问题来求解线性方程组，这种方式有效地避免了SVM的复杂计算过程，从而缩短了求解时间[6]。目前，LS-SVM应用于建模、模式识别、软测量、故障诊断等方面[7]。

yi=f(xi)=〈w,φ(xi)〉+b

(1)

式中：〈,〉表示点积；w表示权重向量；b表示偏差；φ(xi)表示原始变量数据映射以后的值。LS-SVM相应的优化问题转化为公式(2)所示：

(2)

s.t:yi=wT·φ(xi)+b+ξi,i=1,2,…,m

式中：c为惩罚参数；ξi为误差变量。

利用目标函数和约束条件建立的拉格朗日函数为公式(3)所示：

(3)

式中：αi(i=1,2,…,m)代表乘子。

根据优化条件

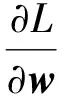
(4)

可得

(5)

上式的另一种表示方式如公式(6)所示：

(6)

式中：Ωij=φ(xi)Tφ(xj)=K(xi,xj)为核函数；Y=[1,…,1]T，Y为m×m阶单位矩阵；α=[α1,…,αm]T为乘子；y=[y1,…,ym]T，最后计算的LS-SVM估计函数如公式(7)所示：

(7)

式中：K(x,xi)=〈φ(x),φ(xi)〉为核函数。

(8)

2 ARMA模型及其定阶

自回归滑动平均(Autoregressive Moving Average, ARMA)[8-9]模型奠定了时间序列时域分析方法的基础。

模型的一般形式为：

(9)

用Bk表示k步线性推移算子，即Bkxt=xt-k,Bkat=at-k，Bkc≡c，c为常数。

并令

φ(B)=1-φ1B-φ2B2-…-φpBp

(10)

θ(B)=1-θ1B-θ2B2-…-θqBq

(11)

则可简记为：

φ(B)xt=θ(B)at

(12)

式中的形式可以记作ARMA(p,q)模型，表示p阶自回归、q阶滑动平均模型。

通常采样时间序列是不平稳的，因此，首先要判断采样序列是否平稳，若为非平稳可以采用差分来消除这种不平稳因素的影响，若差分后的序列均值趋于零，则认为序列是均值化的，否则序列要进行均值化处理。时间序列可以通过数据内部的相互关系来辨识系统的变化规律，它的建模方法是将系统的输出看作是在白噪声输入下的对应[10-11]。

将平稳化后的时间序列通过计算自相关与偏相关系数来判定模型的阶数。模型的定阶原则如表1所示。

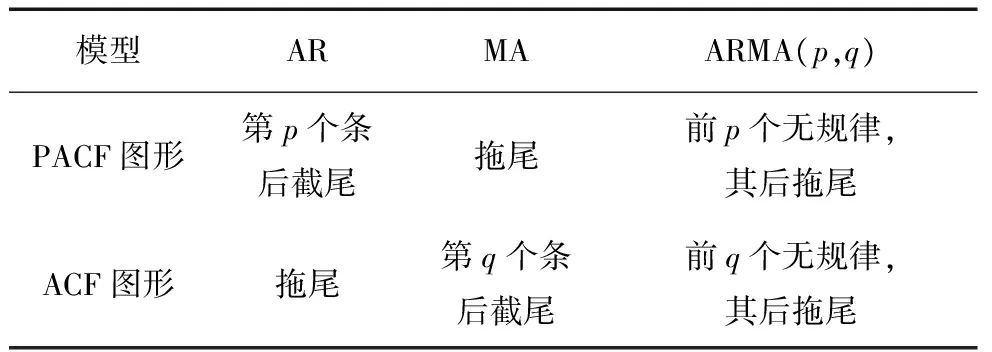
表1 ARMA模型的定阶原则

拖尾是指图形成衰减的指数型波动形式；截尾的k=p代表的是当k>p步时，其后的任意数趋于零。

3 建立基于LSSVM-ARMA动态软测量模型

基于 LSSVM-ARMA动态软测量模型结构如图1所示。

图1 LSSVM-ARMA模型结构图

通过结构图可以看出，模型的建立步骤如下：

3.1 输入变量的选择

由文献[12-16]可知影响NOx生成量的主要因素有：总煤量、总风量、二次风总风量、A、B、C、D、E、AA、AB、CD、DE、EE共10层二次风挡板开度、3层燃烬风挡板开度、烟气温度和烟气含氧量。

采集以上原始变量的历史运行数据，用拉依达法对样本中波动超出正常范围的值预处理，将预处理后的原始输入变量数据进行相关性分析得到输入变量间的相关系数关系如图2所示。

图2 Pearson相关系数关系

由图2可知，各个变量之间存在着正相关和负相关，部分输入变量之间存在着较强的相关性，因此，需要在建立NOx排放模型之前对输入变量进行主元分析(PCA)，从降维后的主元中选出主要变量。经过PCA后的主成分贡献率及累计贡献率如图3所示。

图3 主成分贡献率及累计贡献率

设累计贡献率的要求为80%，选择的主元个数为4，采用PCA方法计算前4个主元上的载荷，主元1输出结果如图4所示。

图4 主元1得分贡献率

由图4可知，在主元1中变量1、变量7与变量8的贡献率较高，对应的辅助变量为总煤量、D层与E层二次风挡板开度。同理得出其他3个主元上的辅助变量。最后选出主元为：总煤量、总风量、A、B、D、E和AA层二次风挡板开度。

3.2 建立基于LS-SVM的静态软测量模型

将总煤量、总风量、A、B、D、E和AA层二次风挡板开度作为输入变量，脱硝反应器入口的NOx生成量输出变量，建立LS-SVM的静态软测量模型，模型的训练结果及相对误差的预测结果如图5和图6所示。

图5 LS-SVM训练结果

图6 LS-SVM训练模型相对误差

3.3 基于静态模型的动态校正

将LS-SVM的训练值与测量值的偏差当作一组时间序列来处理，通过计算自相关与偏相关系数判断其阶数为：p=3；q=2。则判断出时间序列模型为ARMA(3,2)。利用ARMA(3,2)模型对该时间序列进行建模，得到关于预测误差的ARMA模型。

针对2组不同的样本对LS-SVM模型与LSSVM-ARMA模型进行测试。结果如图7、图8所示。

图7 样本1 NOx浓度预测值

图8 样本2 NOx浓度预测值

文中利用平均误差与均方根误差作为评价指标，分析了模型的准确性。表2为2组样本的LSSVM-ARMA模型与LS-SVM的模型的平均相对误差与均方根误差，通过表2描述统计量可以清楚地看出模型预测效果的优劣。

表2 描述统计量

2组不同样本的测试结果显示，LSSVM-ARMA模型与LSSVM模型的预测值平均误差相差约0.2 mg/Nm3，均方根误差相差约0.03 mg/Nm3。

4 结论

基于最小二乘具有较好的泛化能力，本文分析了影响电站锅炉NOx排放量的因素，建立了基于最小二乘支持向量机的NOx排放量静态模型，用ARMA模型对LS-SVM模型的预测误差进行动态估计，进而实现对静态模型的动态校正，提高了模型的预测精度。预测结果表明：基于LS-SVM-ARMA动态模型预测精度明显高于LS-SVM模型的预测精度，能够满足实际应用的需求。

[1]朱涵. 浙大清洁技术大幅降低燃煤有害排放[N]. 经济参考报, 2015-04-20 (6).

[2]陈荣超. 燃煤电厂脱硝NOx的软测量技术和自动控制优化[J]. 电力科学与工程,2015,31(1):15-19.

[3]赵敏,颜文俊,郑军. 基于广义动态模糊神经网络的电厂锅炉燃烧优化建模[J]. 热力发电,2010,39(3):19-22.

[4]BALAMURUGAN I, GOUNDER V, KULENDRAN B, et al. ANN-SQP approach for NOxemission reduction in coal fired boilers[J]. International Journal of Emerging Electric Power Systems,2012,13(3):449-461.

[5]杜文莉, 官振强, 钱锋. 一种基于时序误差补偿的动态软测量建模方法[J]. 化工学报, 2010,61(2):439-443.

[6]王广龙,吕猛,赵文杰. 基于遗传算法的电站锅炉NOx排放量LS-SVM建模[J]. 自动化与仪器仪表,2016(2):70-72.

[7]卓建坤,焦伟红,宋少鹏，等. 锅炉燃烧优化中NOx预测模型研究进展[J]. 燃烧科学与技术,2016,22(6):531-540.

[8]赵瑜, 薛白, 张建伟. 基于ARMA模型的桥梁结构模态参数辨识研究[J]. 华北水利水电大学学报, 2015,36(2):21-24.

[9]孙慧芳,桂中华,李林扬，等. 基于时间序列组合模型的水电机组状态趋势预测[J]. 水力发电学报,2016,35(1):79-86.

[10]喻敏,常毓婵,袁浩,等. 基于HP-EMD和ARMA的短期风速预测[J]. 中国科技论文,2016,11(5):566-570.

[11]李生彪. 基于ARMA模型的故障率时间序列预测[J]. 自动化与仪器仪表,2015(12):218-219.

[12]童小川. 燃煤电厂氮氧化物NOx排放控制研究[D].北京:华北电力大学,2016.

[13]李建强,姜翻,汪安明，等. 粗糙集在控制燃煤电厂NOx排放中的应用[J]. 电力科学与工程,2014,30(12):19-23.

[14]李永华,李金芳,郝晓路. 不同粒径下低氮燃烧时含S产物和NOx释放特性的实验研究[J]. 华北电力大学学报(自然科学版),2017,44(3):99-105.

[15]吕游, 刘吉臻. 基于PLS特征提取和LS-SVM结合的NOx排放特性建模[J]. 仪器仪表学报, 2013,34(11):2418-2424.

[16]GUO Y F, BU Y D, HE F L,et al. Numerical Simulation Study on Nitrogen Oxides Emissions of Power Plant[J]. Applied Mechanics and Materials,2013,2301(295):915-918.

Research on Dynamic Soft Sensing of NOxEmission for Utility Boiler Based on LSSVM-ARMA

YUAN Hong， SONG Xuanfeng， ZHAO Zheng

(School of Control and Computer Engineering, North China Electric Power University, Baoding 071003，China)

An accurate NOxemission model is the cornerstone of the boiler optimization and NOxreduction. To improve the forecast accuracy of NOxemissions, a dynamic soft measurement of NOxemissions is proposed, which is based on least-square support vector machine (LS-SVM) and auto regress moving average (ARMA). According to the historical operation data of a 330 MW unit in some power plant, firstly, a static soft sensor model of NOxemission based on least-square support vector machine is established. Secondly, the dynamic correction of the static model is realized by the auto regressive moving average method. Finally, the lssvm-arma model and LS-SVM model are validated through two different sets of samples, and hence the average error and root mean square error of the two models are obtained. The results show that compared with the LS-SVM, the combination of LS-SVM and ARMA has higher prediction accuracy, and it is effective for the prediction of NOxemissions of the power plant boilers.

dynamic soft sensing；least squares support vector machines；ARMA；NOxemission

2017-08-16。

新能源电力系统国家重点实验室开放课题资助(LAPS16008)；中央高校基本科研业务费专项资金资助项目(2017MS133)。

10.3969/j.ISSN.1672-0792.2017.12.009

TK321

A

1672-0792(2017)12-0050-05

袁洪(1992-)，女，硕士研究生，研究方向为热工过程控制及建模。