高压直流输电线路两极短路接地故障测距研究

崔本丽， 兰 生， 黄晶晶， 种佳丽

(福州大学 电气工程与自动化学院，福建 福州 350108)

高压直流输电线路两极短路接地故障测距研究

崔本丽， 兰 生， 黄晶晶， 种佳丽

(福州大学 电气工程与自动化学院，福建 福州 350108)

小波分析已被广泛应用于高压直流输电线路的故障测距之中，但多数也仅局限于对单极接地故障的测距研究。在此基础上，提出利用小波变换的模极大值理论对两极短路接地故障进行分析。首先，在PSCAD中搭建出高压直流输电系统的仿真模型并进行故障线路仿真，得到故障时的暂态电流信号，最后，对电流行波进行小波分析实现故障测距。从仿真分析结果可知，该方法的定位误差不超过线路全长的0.5%，证明了小波变换的模极大值理论可适用于两极短路接地的故障测距中。

小波分析； 高压直流输电； 两极短路； 双端测距； 模极大值理论

0 引言

对于HVDC输电系统来说，直流输电线路故障类型主要有单极线路对地故障、两极线路短路故障以及两极线路短路接地故障[1]。大量资料表明，目前对于直流输电线路故障测距方法的研究主要是基于单极线路对地故障开展的，而对双极线路故障很少涉及。虽然双极同时故障很少发生，但一旦出现，系统就会甩掉所有负荷，而且它很有可能是永久性故障，危害性极大。因此，对直流输电线路两极故障的研究是很有必要的。本文将从两极线路短路接地故障测距的分析入手进行两极故障的研究。

当输电线路发生两极短路接地故障时，线路上会有暂态电流、电压行波产生，即使它们行进到母线测量端，也带有不规则的突变特征[2]。小波变换具有时频局部化、去噪能力强等特征，适合对突变信号进行检测[3-5]，因此多被用于输电线路的故障测距之中。文献[6]提出基于小波变换模极大值理论的双端测距方法，该方法首先记录下初始故障电流行波波头到达HVDC输电线路两端的时间，最终利用双端法原理计算出故障点距离逆变侧母线的长度；文献[7]通过对故障暂态电压信号进行小波变换，提出一种单级和双级HVDC输电线路均适用的故障测距方法；文献[8]利用相同的小波变换模极大值理论，但实现的是单端行波故障测距。文献[9]提出了基于小波变换的HVDC输电线路故障定位原理。由上述分析可知，小波分析早已被用于HVDC输电线路的故障测距之中，但也只是对单极接地故障的分析，本文将尝试利用小波分析的模极大值理论对两极线路短路接地故障情况进行测距研究。

1 小波分析的模极大值理论

设Wsf(x)(s=2j)是函数f(x)的小波变换，在尺度s下，在x0的某一邻域a，对一切x均有：

|Wsf(x)|≤|Wsf(x0)|

(1)

则把x0称作小波变换的模极大值点，Wsf(x0)称作小波变换的模极大值。

从上述小波变换的模极大值理论可以看出，如果小波函数被视为某一平滑函数的一阶导数时，那么由它变换得到的信号小波变换模的局部极值点与信号的突变点是一一对应的；如果小波函数被视为某一平滑函数的二阶导数时，那么由它变换得到的信号小波变换模的过零点与信号的突变点也是一一对应的关系。这也就是说，小波变换的模极大值对应着信号的突变点，而极大值的极性和大小分别表示突变点的变换方向和变化强度，因此，可根据小波变换的模极大值点标识出非平稳信号的突变点[10]。

HVDC输电线路故障时会产生高频电流暂态行波分量，该电流行波分量实质上就是一种非平稳信号，而故障后在线路两端检测到的初始电流行波波头、故障点反射电流波与行波电流信号的突变点相互对应，具有较大的奇异性。本文通过对故障发生后的暂态电流行波进行小波分析，得到故障初始行波到达两侧检测点的时间以及故障点反射行波到达整流侧的时间，然后计算出故障距离，从而实现双端行波故障测距。

在时间轴上，二进小波具有平移不变性的良好特征。在所有多项式函数中，B样条函数具有最小支撑的优点且能够检测突变信号，文献[11]将3次B样条函数用于电缆单环网的故障测距中。本文将两者结合，选用3次中心B样条函数对两极短路接地故障暂态电流行波信号进行二进小波变换，进而实现故障测距。

2 故障测距原理

本文采用不受波速影响的双端行波故障测距法[12]。与单端法相比，双端法虽然需在线路两端装设测距装置，使用设备多，经济性较差，但正因为测距设备的增多，才能够获得更加丰富的行波信息，增加了行波故障定位的可靠性。

图1为该测距方法的原理图，其中输电线路总长度为L，故障点F到整流侧A端的距离为x。为了方便计算，文中把故障发生的绝对时刻记为t0，把故障初始行波到达整流侧A端和整流侧B端的时刻分别记为t1、t3，故障点反射行波到达整流侧A端的时刻记为t2，另外认为在故障发生之后的较短时间内，行波以固定不变的波速v(未知)向线路两侧传播。根据上述条件有以下等式成立：

(2)

通过联立方程，求得故障距离：

(3)

上式中不含波速，因此便消除了波速对测距的影响。

图1 不受波速影响的双端故障测距原理图

3 仿真分析

3.1 仿真模型

本文利用电磁暂态仿真软件PSCAD/EMTDC，搭建出如图2所示的±500 kV双极性12脉波HVDC输电系统的仿真模型，其中直流侧装设12、24、36次的直流滤波器来抑制直流电压和电流中的谐波，交流侧装设11、13、23、25次的交流滤波器来抑制交流谐波。

图2 ±500 kV双极性12脉波HVDC输电系统仿真模型

为了方便在不同位置处设置故障，在模型中搭建了两段双极输电线路，具体结构如图3所示。该结构中传输线路总长度为800 km，两极传输线路直流电流为±1 kA，线路总传输功率为1 000 MW，系统采样频率设为200 kHz，仿真运行时长为2 s。在对直流传输线路进行故障仿真时，采用频变参数(相位)模型进行模拟，因为该模型最为准确，使用范围最为广泛，其杆塔结构如图4所示。本文参照高肇、三—常直流输电系统中ACSR720/50型钢芯铝绞线的参数，采用4分裂导线布置方式，子导线分裂间距为0.5 m，计算半径r=18.1 mm，在20 ℃温度下直流电阻Rd=0.039 84 Ω/km，杆塔高度为20 m，两极传输线路间距为17.365 m，弧垂设为10 m，不考虑架空地线等影响，直流线路沿线大地电阻率为1 500 Ω·m[13]。

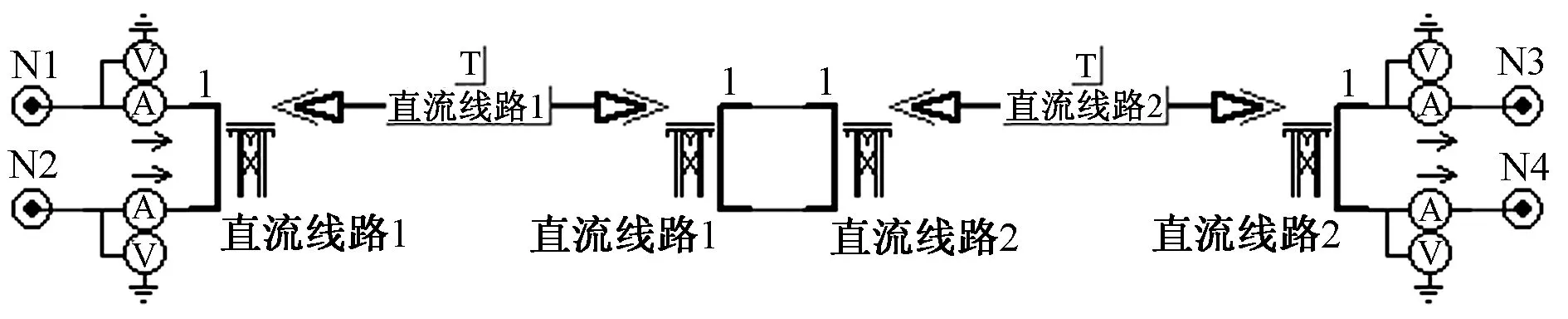
图3 直流输电线路模块

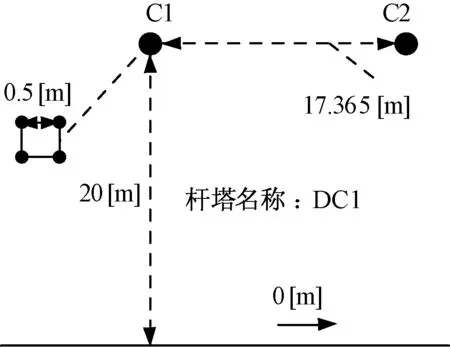
图4 直流输电线路杆塔结构

3.2 相模变换

本文所研究的为双极直流输电系统的输电线路，图5为其简易模型。实际工程中双极输电线路两极之间存在耦合，在计算沿线电流分布时，首先需要对线路方程进行解耦[14]，使其成为相互独立的模量，以便计算。

图5 双极直流输电系统简易模型

对于存在互感的输电线路AB，满足微分方程：

(4)

式中:

(5)

式中：uA1、uA2分别是线路A端正极、负极电压；iA1、iA2分别是线路A端正极、负极电流；Rs、Rm分别为HVDC的自阻、互阻；Ls、Lm分别为HVDC的自感、互感；Gs=Gm+G0，Gm为两极间的电导，G0为极对地的电导；Cs=Cm+C0，Cm为两极之间的电容，C0为极对地的电容。

对于上式微分方程，通常可构造如下解耦矩阵：

(6)

通过解耦矩阵，上式可改写成如下形式：

(7)

式中：

(8)

令上式中

(9)

称u1、i1为1模(也称线模)电压、电流，u0、i0为0模(也称地模)电压、电流，则HVDC相应的1模、0模参数分别为：

(10)

由上述分析可知，解耦之后的模量间不存在互感的影响，计算较为方便。但0模(零模)分量受线路地理环境和频率影响较大，而1模(线模)分量受频率影响较小，因此1模分量比0模分量稳定[15]。为了适应各种不同故障的影响，本文选用线模分量进行计算。

3.3 仿真结果和讨论分析

在距离输电线路整流侧300 km处设置金属性两极短路接地故障，故障开始时间设为仿真开始后的1 s，故障持续时间为0.05 s。仿真后可在线路两端测量点处得到如图6所示的正极线路电流波形(负级线路电流变化形式与此相同，不一一列出)。

图6 正极线路故障电流波形

对故障电流行波进行相模变换并从1 s开始采集2 048个点进行故障分析，图7即为故障发生后整流侧的线模电流波形，图8为该波形在不同尺度下 (21，22，23)小波变换的模极大值。

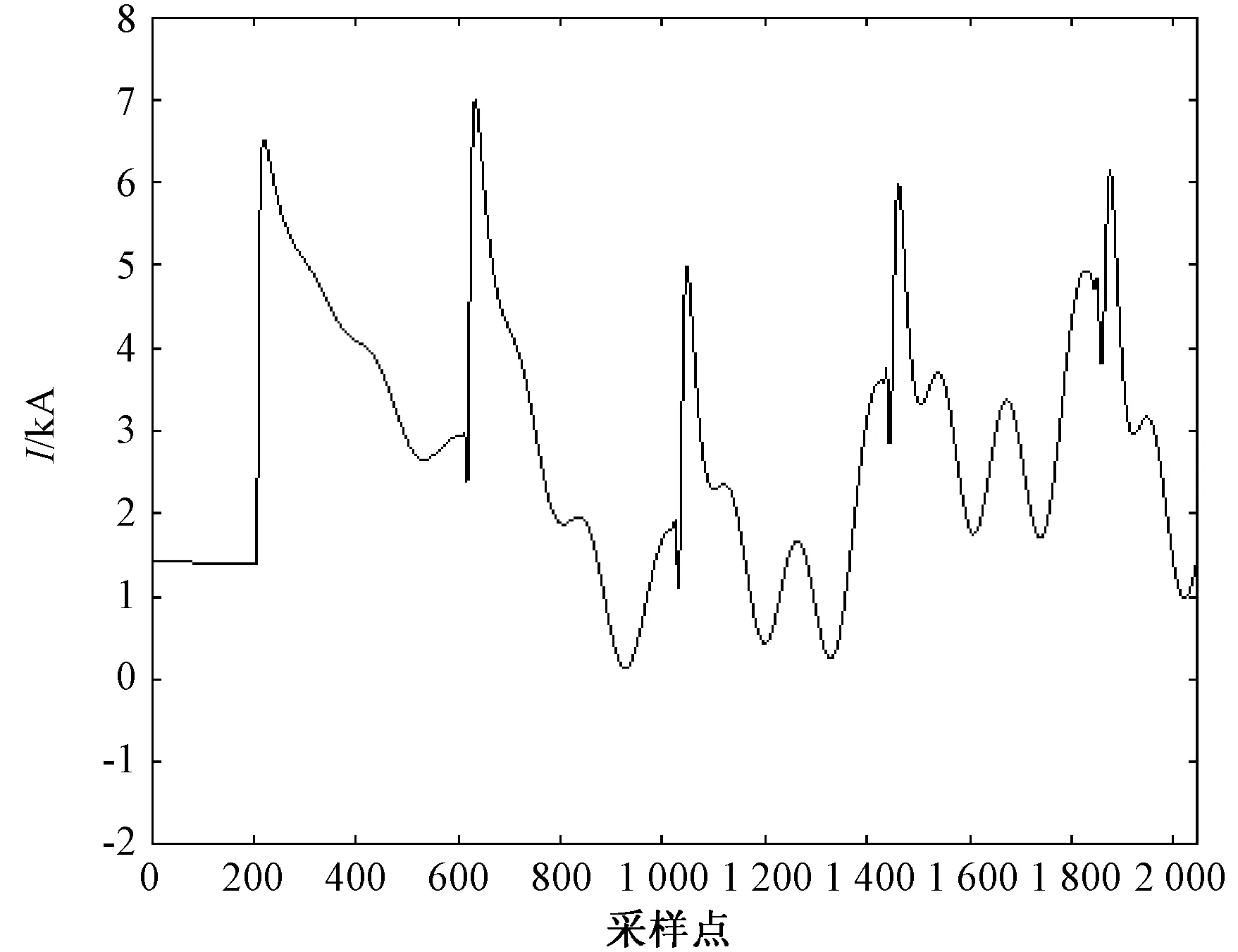
图7 整流侧线模电流

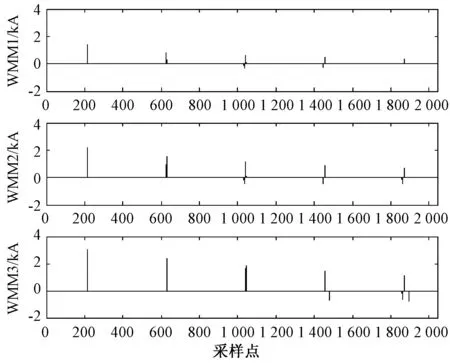
图8 整流侧线模电流在不同尺度下(21，22，23)的小波变换模极大值

由小波变换的模极大值图形可知，在采样点214处故障电流初始行波到达整流侧，在采样点628处故障电流反射行波到达整流侧，它们所对应的时刻分别为：t1=1+214×5×10-6=1.001 070 s，t2=1+628×5×10-6=1.003 140 s。

图9和图10分别为故障发生后逆变侧的线模电流及其该线模电流在不同尺度下(21，22，23)小波变换的模极大值。

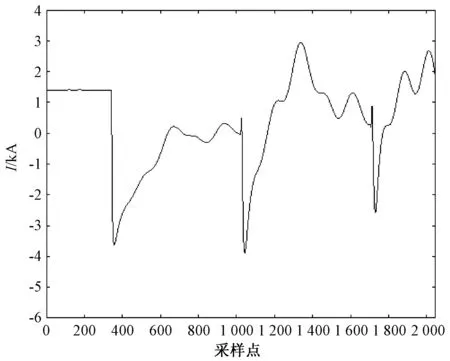
图9 逆变侧线模电流

图10 逆变侧线模电流在不同尺度下(21，22，23)的小波变换模极大值

由图10可看出，在采样点351处，故障电流初始行波首次到达逆变侧，其对应的时刻t3=1+351×5×10-6=1.001 755 s。

将t1，t2，t3和线路长度L均代入公式(3)中，可求出故障距离：x=300.544 5 km。其对应的测距误差Δx=x-x1=0.544 5 km，其中x1为故障点距离整流侧的实际距离；测距相对误差e=Δx/L=0.068 1%。

按照上述小波分析的方法，分别在距离整流侧0 km，100 km，200 km，400 km，500 km，600 km，700 km，800 km处设置双极短路瞬时性金属接地故障，并将故障信息和测距结果列入表1中。

从上述测距结果可以看出，在线路中点发生故障时的定位误差最小，因为此时两端的波阻抗大小相等，不会受到反射波的影响；当故障位置距离整流侧、逆变侧较近时，误差较大，最大测距误差可达2.545 5 km，但即使是最大定位误差也不超过线路全长的0.5%，即小波变换的模极大值理论在两极短路接地故障测距中具有一定的可行性和准确性，能够实现全线范围内的精确定位。

表1 双极短路金属性接地故障的测距仿真结果

4 结论

当高压直流输电线路发生两极短路金属性接地故障时，故障后的暂态电流行波中包含故障距离信息。本文首先对故障后测量点处的电流行波信号进行解耦运算，然后采用3次B样条函数作为小波函数对解耦后的线模分量实行二进小波变换，并利用小波变换的模极大值理论找出故障点初始行波到达整流侧的时刻t1，故障点反射行波到达整流侧的时刻t2，故障初始行波到达逆变侧的时刻t3，然后利用不受波速影响的双端故障测距方法计算出故障位置。为了验证该方法的可行性，分别在距离整流侧不同位置处设置两极短路瞬时性金属接地故障。从一系列测距数据可看出，基于小波变换的行波法可以用于两极短路故障的测距研究中，且定位精度基本不受双极短路接地故障发生位置的影响，这也为两极短路故障的研究提供了思路和方法。

[1]束洪春, 刘可真, 朱盛强,等. ±800 kV特高压直流输电线路单端电气量暂态保护[J]. 中国电机工程学报, 2010，30(31):108-117.

[2]高洪雨, 陈青, 徐丙垠,等. 输电线路单端行波故障测距新算法[J]. 电力系统自动化, 2017，41(5):121-127.

[3]唐珂, 谢源, 曾明杰. 基于小波变换的风电机组故障诊断方法研究[C]//太原：风能产业，2016.

[4]钱国超, 赵仲勇, 邹德旭,等. 基于连续小波变换的变压器绕组变形故障类型检测[J]. 高电压技术, 2017, 43(6):2016-2023.

[5]MANGALGE S, JAWALE S. Location of fault in long HVDC transmission line using continuous wavelet transform[C]//USA:International Conference on Signal Processing, Communication, Power and Embedded System, 2016.

[6]赵妍卉, 王少荣. 基于小波模极大值理论的HVDC输电线路行波故障定位方法的研究[J]. 电力系统保护与控制, 2007, 35(1):13-17.

[7]CHEN P, XU B, LI J, et al. Modern travelling wave based fault location techniques for HVDC transmission lines[J]. Transactions of Tianjin University, 2008, 14(2):139-143.

[8]王永治. 基于小波模极大值的高压直流输电线路电弧故障定位[J]. 云南电力技术, 2008, 36(2):1-4.

[9]HAN H X, YU Y, YI R P, et al. Novel scheme of travelling wave based differential protection for bipolar HVDC transmission lines[C]//USA:International Conference on Power System Technology, IEEE, 2010.

[10]刘飞霞, 成志威, 赵雨晴. 基于小波变换的变压器励磁涌流识别方法[J]. 电力科学与工程, 2014,30(3):54-58.

[11]王敏, 王磊, 陈平. 基于行波原理的10 kV电缆单环网故障测距研究[J]. 电力系统保护与控制, 2013,41(6):38-42.

[12]胡文斌, 廖玄, 康毅,等. 一种不受波速影响的双端行波故障定位方法[J]. 陕西电力, 2016, 44(2):39-42.

[13]LIU P, CHE R, XU Y, et al. Detailed modeling and simulation of ±500 kV HVDC transmission system using PSCAD/EMTDC[C]//USA:Power and Energy Engineering Conference, IEEE, 2016.

[14]康丽红, 唐昆明, 罗建,等. 直流输电线路单极接地双端故障测距[J]. 电网技术, 2014, 38(8):2268-2273.

[15]周聪聪, 舒勤, 韩晓言. 基于线模行波突变的配电网单相接地故障测距方法[J]. 电网技术, 2014, 38(7):1973-1978.

Research on Two-pole Short-circuit Earth Fault Location of High Voltage Direct Current Transmission Lines

CUI Benli， LAN Sheng， HUANG Jingjing， CHONG Jiali

(College of Electrical Engineering and Automation，Fuzhou University， Fuzhou 350108，China)

Currently, wavelet analysis has been widely applied to fault location of high voltage direct current(HVDC) transmission lines, but it is only limited to the study range of monopolar earth fault. Based on this situation, the wavelet transform modulus maxima theory is put forward to analyze the two-pole short-circuit earth fault. First, the simulation model of HVDC transmission system is built in PSCAD and some simulations for fault lines are carried out to obtain the transient current signal. Hence, the fault location is realized by analyzing the traveling wave of the current using wavelet analysis. The simulation results show that the positioning error is less than 0.5% of the line length, which proves the wavelet transform modulus maxima theory can be applied to two-pole short-circuit earth fault location of HVDC transmission lines.

wavelet analysis; HVDC transmission; two-pole short-circuit earth fault; double-terminal fault location; modulus maxima theory

2017-07-19。

10.3969/j.ISSN.1672-0792.2017.12.002

TM726

A

1672-0792(2017)12-0009-06

崔本丽(1993-)，女，硕士研究生，主要从事高压直流输电线路的故障测距研究。