基于TEAM P21基准模型的杂散损耗测量方法研究与验证

刘 涛， 刘兰荣， 张俊杰， 聂京凯， 程志光， 金文德

(1. 保定天威保变电气股份有限公司，河北 保定 071056； 2. 全球能源互联网研究院，北京 102211； 3. 国网浙江省电力公司，浙江 杭州 310007)

基于TEAM P21基准模型的杂散损耗测量方法研究与验证

刘 涛1， 刘兰荣1， 张俊杰1， 聂京凯2， 程志光1， 金文德3

(1. 保定天威保变电气股份有限公司，河北 保定 071056； 2. 全球能源互联网研究院，北京 102211； 3. 国网浙江省电力公司，浙江 杭州 310007)

基于TEAM P21基准模型，结合电磁场仿真软件，对不同频率下导磁构件的杂散损耗问题进行了实验及仿真计算研究。在TEAM P21基准问题中，由于导磁构件会对励磁线圈的漏磁通带来影响，所以传统的通过负载(励磁线圈加结构件)损耗减掉空载(励磁线圈)损耗得到的导磁构件损耗会带来一定误差。为避免此误差，提出了一种测量导磁结构件杂散损耗的新方法，即在仿真软件可对励磁线圈(铜线圈，线性材料)损耗进行较准确计算的前提下，通过仿真计算得到有空载及负载工况条件下的励磁线圈损耗差并对实验结果进行修正。所提出的测量方法和获得的实验数据有助于得到更准确的导磁构件杂散损耗实验结果并有助于提高仿真计算的准确性。

TEAM P21基准问题； 漏磁通； 杂散损耗； 硅钢叠片

0 引言

输变电装备中的杂散损耗问题，对试验研究和数值仿真而言都是一个复杂的经典难题。以大型电力变压器为例，杂散损耗系因变压器漏磁场在导电实体或导磁构件中感应产生，杂散损耗的局部密度过大，可能引起局部过热，危及变压器安全运行。对于高压、特高压变压器，杂散损耗和发热冷却问题的研究就显得更为突出，不可忽视任何一个导致杂散损耗密度过度增加或过热的结构细节[1]。

电磁场数值模拟仿真的有效性依赖于分析方法、计算软件、材料属性数据及充分的实验验证。为了验证数值模拟仿真方法的有效性，从1985年开始，国际电磁计算协会(ICS)一直非常关注世界范围内的TEAM基准问题，为了测试及比较电磁场数值分析计算方法，建立了一系列到目前仍被广泛应用的基准问题族[2]。此外，还发布了用于验证计算电磁学中模拟及仿真的IEEE标准[3]。

TEAM P21基准问题以模拟电气工程中的杂散损耗问题为背景提出，目前已有包括5组16个基准模型族[4-8]。在实验研究方面，结构件的杂散损耗总是与其他损耗成分混在一起，因而，不能直接测量杂散损耗，很难准确地将结构件上的损耗从总损耗中分离出来。因此，如何能更准确地得到结构件损耗，仍是在研究杂散损耗问题中需要重点解决的问题之一[9-15]。本文基于TEAM P21基准问题中的P21c-M1及P21-B基准模型，结合Infolytica公司的MagNet电磁场仿真软件，对不同频率下取向硅钢叠片的杂散损耗问题进行了研究。提出了一种确定导磁构件杂散损耗的新方法，并对该方法的有效性进行了验证分析。更有效的损耗测量数据有助于提高仿真计算的准确性。

1 杂散损耗测量方法研究

1.1 磁场及损耗仿真计算

传统的测量方法是采用负载(含结构件)总损耗Pload减去空载(无结构件)励磁线圈损耗Pnoload来得到结构件的杂散损耗Pt。

Pt=Pload-Pnoload

(1)

激励线圈中的欧姆损耗包括线圈中的涡流损耗和直阻损耗，其中涡流损耗由漏磁场在铜导线中感应产生。实际上，当结构件为导磁材料时，对于线圈来说，负载工况条件下与空载工况条件下的漏磁场分布是有差异的。利用仿真软件可计算得到励磁线圈周围的二维漏磁场分布。图1所示为P21基准模型在反向激励、空载工况条件励磁线圈周围二维磁场分布。图2为P21基准模型在反向激励、负载工况条件下，当构件为硅钢叠片时励磁线圈周围的二位漏磁场分布。

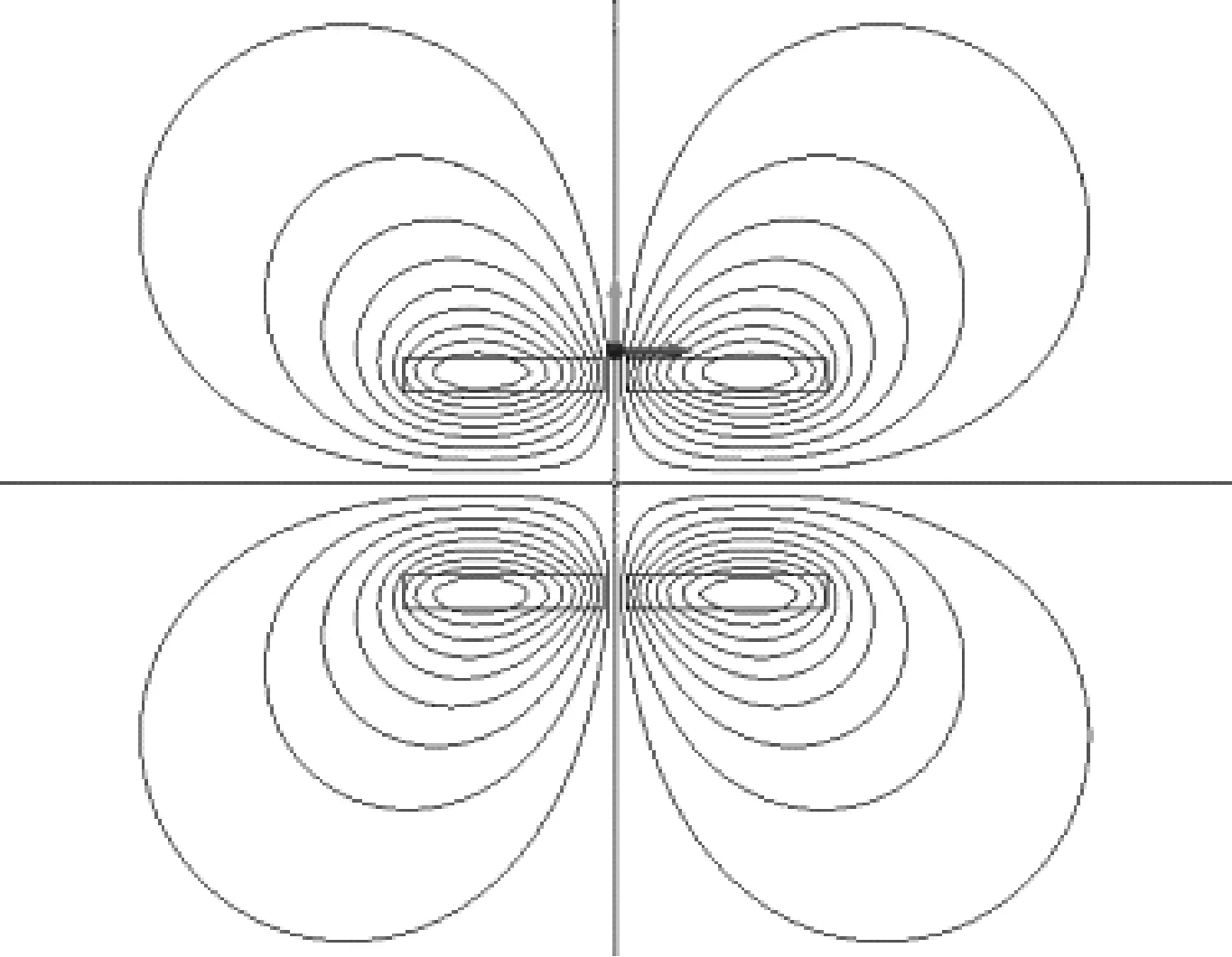
图1 空载条件下励磁线圈漏磁场分布

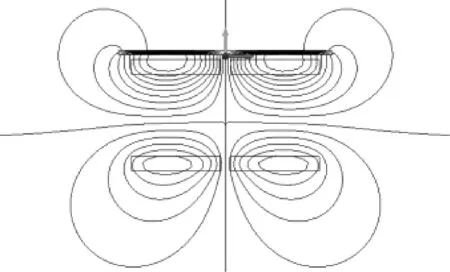
图2 负载(硅钢叠片)条件下励磁线圈漏磁场分布

从图中可看出，2种工况条件下励磁线圈周围的漏磁场分布有明显差异，从而导致励磁线圈的涡流损耗差异。采用传统的“负载—空载”的测量方法会带来一定的误差。因此，在利用TEAM P21模型研究构件杂散损耗问题时，应当充分考虑负载和空载时励磁线圈的损耗差因素。

相对于非线性导磁材料，线性导磁材料(铜线)的损耗仿真更易得到准确的计算结果。为验证仿真软件对线性导磁材料仿真计算的准确度，对P21基准模型的励磁线圈做了建模仿真及实验验证。由于建模的精细程度会直接影响计算结果，为了得到更准确的线圈损耗仿真计算结果，对励磁线圈进行了单匝建模，模型中的每一匝都和实际结构对应，以使建模结构更接近实际线圈模型，考察仿真计算对线性空载线圈损耗计算的有效性。图3为P21基准模型励磁线圈的1/4模型图。

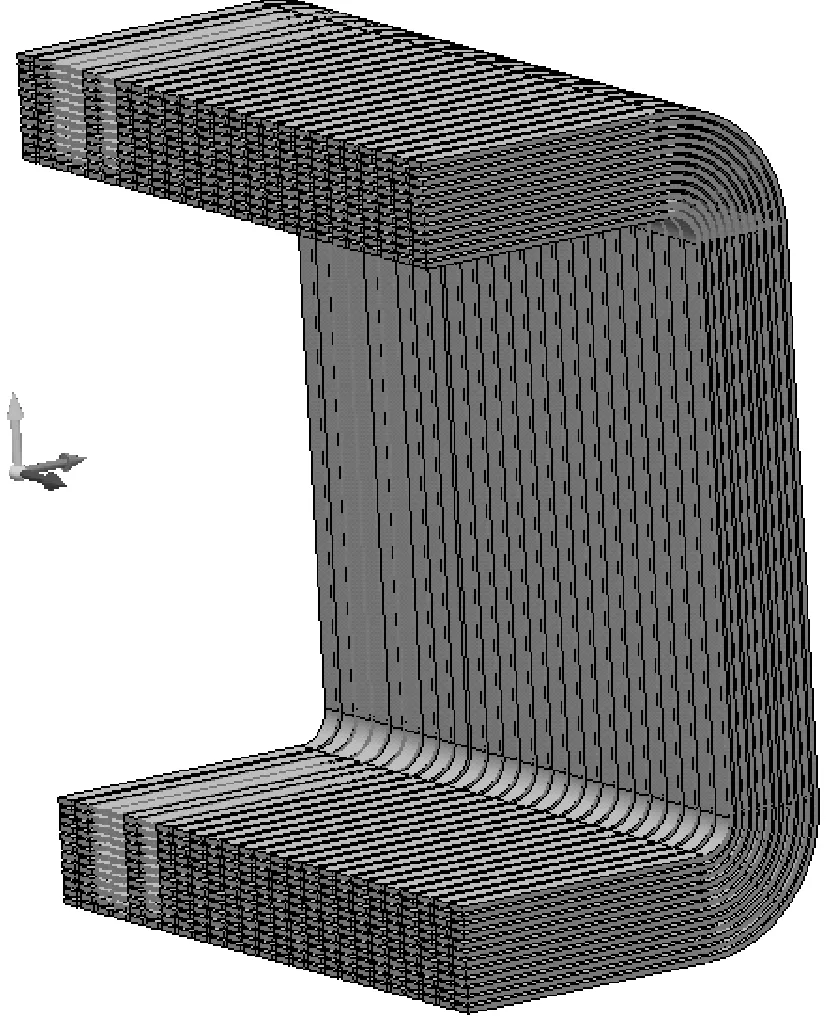
图3 线圈模型图

激励线圈(铜导线)的电阻会受到温度影响，在相同激励电流条件下，不同环境温度会有不同的线圈损耗。如P21基准模型在10 A反向激励条件下，当环境温度为20 ℃时，线圈测量损耗为73.35 W，而当环境温度为30 ℃时，线圈损耗则达到76.62 W。因此，在仿真计算时，需考虑环境温度对铜导体材料电导率的影响并修正，才能得到更合理准确的仿真计算结果。

在环境温度为30 ℃条件下，在不同频率及不同激励电流的条件下测量得到的及计算得到的励磁线圈损耗数据对比分析见表1。

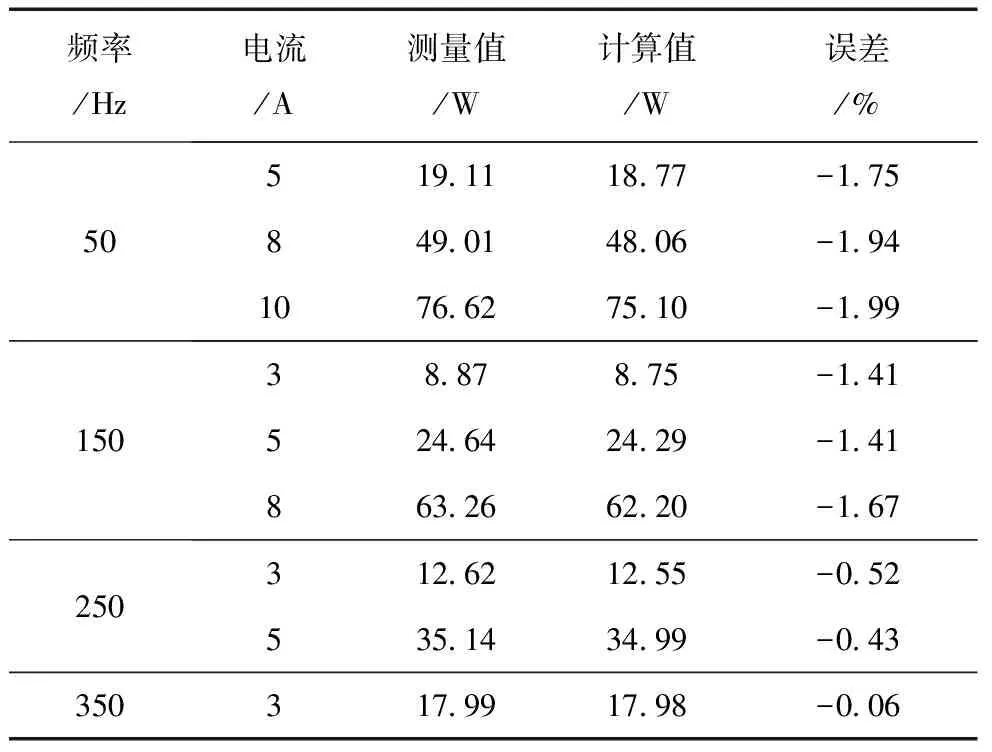
表1 线圈损耗测量及计算结果

从表1中线圈损耗数据可看出，通过仿真软件，采用单匝建模的方式可以较准确地计算得到线圈损耗。计算误差可以控制在2%以内，在激励条件为350 Hz、3 A时的计算误差仅为0.06%。

1.2 改进的导磁构件杂散损耗测量方法

基于空载、负载条件下的漏磁场分布差异给传统测量方法的构件损耗测量带来误差，以及励磁线圈的损耗可通过仿真计算软件较准确地得到。为了能更准确地确定构件损耗，提出了一种考虑激励线圈损耗差的导磁构件杂散损耗测量方法，如公式(2)～(4)所示：

Pcoil_l=Pcoil_n+δ

(2)

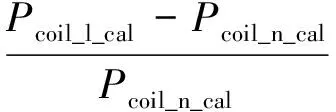
(3)

式中：Pcoil_l为负载工况下线圈的实际损耗；Pcoil_n为空载工况下线圈的实际损耗(即Pnoload)；δ为2种工况之间线圈损耗的差值。Pcoil_l_cal为负载工况条件下线圈的损耗仿真计算值；Pcoil_n_cal为空载工况条件下线圈的损耗仿真计算值。

导磁结构件的实际杂散损耗P为测量的负载总损耗Pload减掉负载工况条件下的实际线圈损耗Pcoil_l可用下式表示：

P=Pload-Pcoil_l

(4)

将式(2)代入式(4)，可得：

P=Pload-Pcoil_l=Pload-Pcoil_n-δ

(5)

式中：Pcoil_n即为Pnoload，将式(1)代入式(5)，可得：

P=Pload-Pnoload-δ=Pt-δ

(6)

式中：Pload为负载工况条件下的总损耗；Pt为传统的“负载—空载”方法得到的构件损耗；P为用改进的新方法处理得到的构件损耗。

2 实验及仿真验证

2.1 硅钢叠片损耗实验及仿真

基于TEAM P21问题中的P21c-M1基准模型，剪切了一组(20片)宝钢B30P105取向硅钢结构件试样。在环境温度为30 ℃条件下，针对改组试样做了损耗测量实验。

为了得到更准确的仿真计算结果，对20片硅钢叠片的每片都进行单片建模。使仿真模型和实验模型在结构上完全对应而不进行简化处理。

P21c-M1的结构图如图4，其模型图如图5。

给P21c-M1基准模型的2个励磁线圈施加不同频率、不同大小的反向激励电流，得到一系列硅钢叠片的损耗测量结果及空载励磁线圈的损耗计算结果见表2。

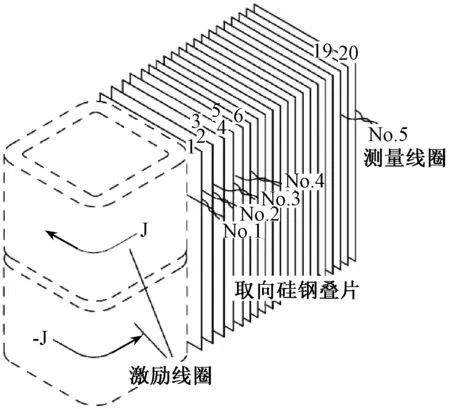
图4 P21c-M1结构图

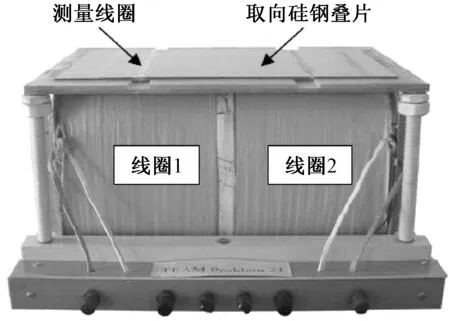
图5 P21c-M1模型图

从表2中数据可看到，在相同激励电流条件下，随着频率的提高，δ与Pt的比值逐渐变大，如在激励电流为5 A，50 Hz时，δ/Pt为0.34；150 Hz时，δ/Pt为0.44；250 Hz时，δ/Pt为0.46。这说明了频率越高，利用传统“负载—空载”方法带来的测量误差越大。

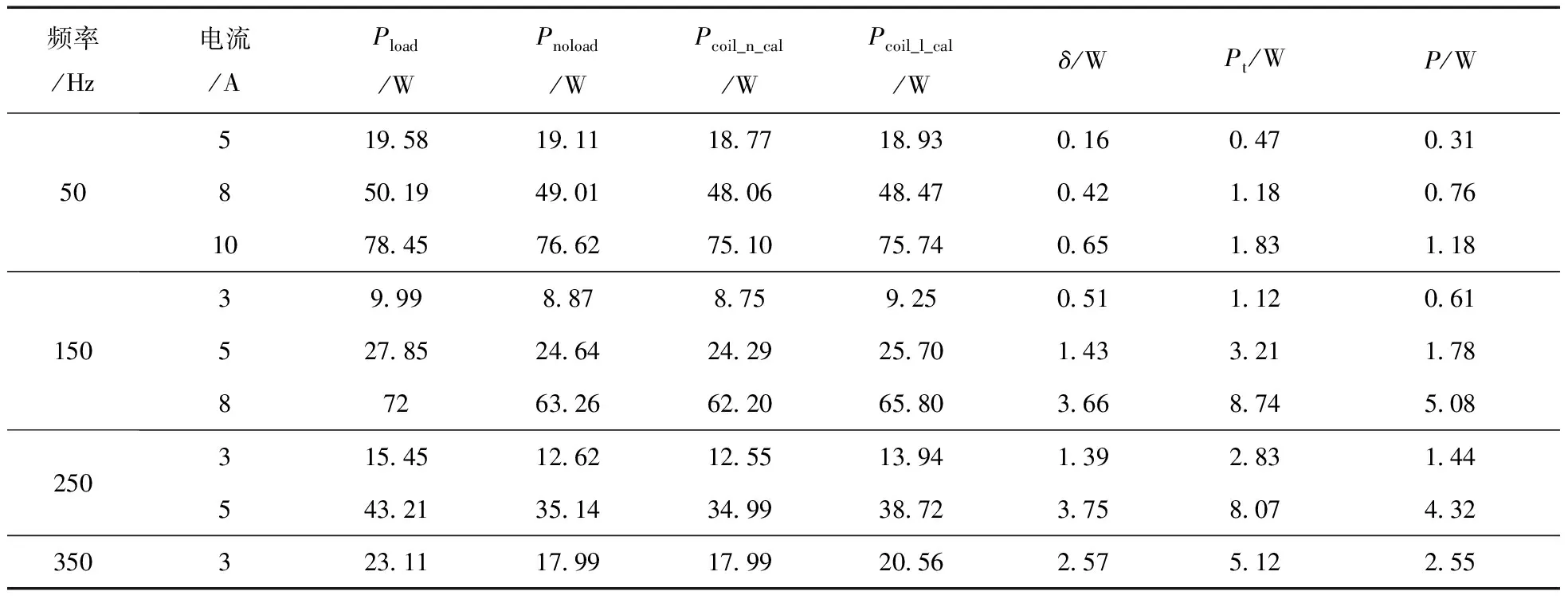
表2 损耗测量及计算结果

B30P105取向硅钢材料在不同频率下的磁性能通过爱泼斯坦方圈测量系统测量得到。

针对该模型进行建模仿真，将构件的20片硅钢片采用分片建模的方式。对于材料的电导率，设为各向异性，轧制方向及垂直轧制方向给正常电导率参数，而在垂直叠片方向，设定电导率为1。如此设置的原因在于，在用爱泼斯坦方圈测量系统进行材料的损耗性能测量时，已经包含了沿硅钢片厚度方向截面的涡流损耗，设电导率为1，避免了截面方向涡流损耗的重复计算。

利用本文提出的新方法处理得到的不同频率条件下硅钢叠片损耗值同计算值的对比见表3，其中，Pcal为硅钢叠片的损耗计算值。

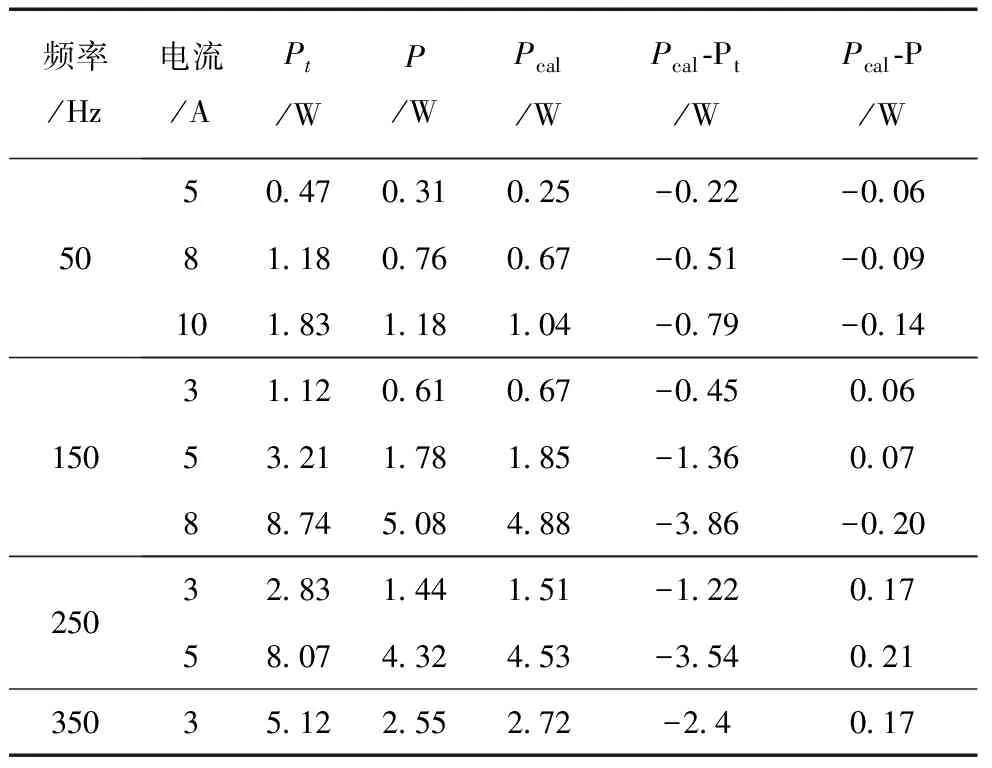
表3 构件损耗处理值及计算值

从处理得到及仿真计算的损耗对比数据来看，仿真结果更接近用本方法处理得到的损耗计算结果。因此，利用仿真手段，考虑空负载漏磁场分布不同所带来的测量误差因素，可以更合理地确定硅钢叠片的构件损耗。

2.2 导磁钢板损耗实验及仿真

除硅钢叠片结构件外，还对TEAM P21-B基准模型(结构件为导磁钢板Q235B)基于本方法做了实验研究及验证。本次基于TEAM P21-B基准模型所做的实验研究及验证也是在30 ℃的环境温度条件下，其模型图如图6。

图6 P21-B模型图

同样给P21c-B基准模型的2个励磁线圈施加不同频率、不同大小的反向激励电流，得到的损耗测量结果及空载励磁线圈的损耗计算结果见表4。

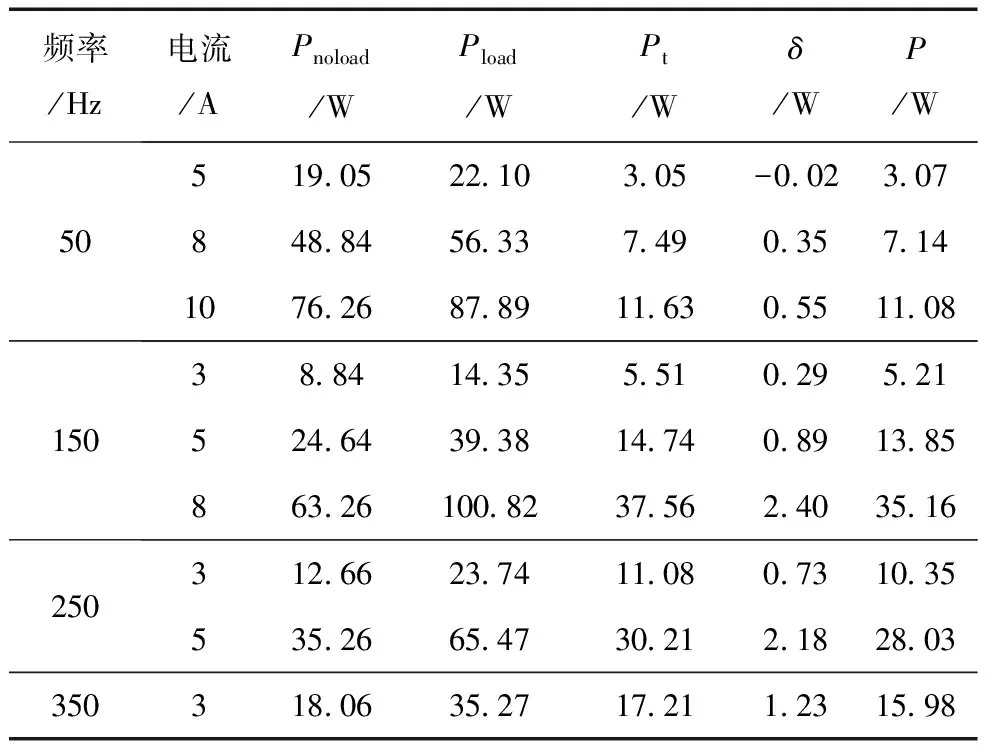
表4 损耗处理及仿真计算结果

利用本文提出的新方法处理得到的不同频率条件下导磁钢板损耗值同计算值的对比见表5，其中Pcal为导磁钢板的损耗计算值。

从数据对比来看，在50 Hz工频激励条件下，计算值更接近传统“负载—空载”方法得到的损耗值，当频率为150 Hz及以上时，计算值更接近用本文提出的新方法处理得到的损耗值。这也说明了随着频率提高，传统“负载—空载”方法带来的测量误差增大。

此外，对比P21c-M1与P21-B 2个基准模型，将2组构件的损耗计算值分别同用本方法处理得到的损耗数据相比，P21c-M1比P21-B的损耗计算值有更好的吻合度。分析原因，是由于硅钢叠片的导磁性能比导磁钢板好，导磁构件的导磁性能越好，“负载—空载”所带来的测量误差越大，越适合用本方法去测量构件损耗。

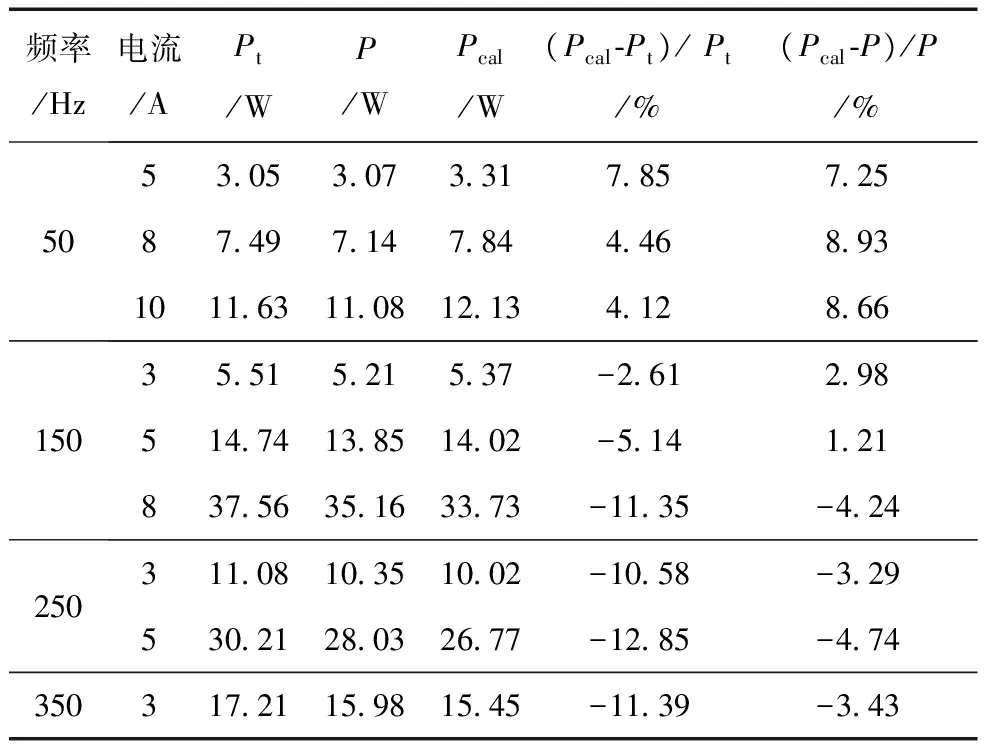
表5 构件损耗处理值及计算值

3 结论

本文在TEAM P21基准问题传统测量方法的基础上，提出了一种导磁结构件杂散损耗测量新方法，通过实验及仿真结果的对比，可得出如下结论：

(1)在仿真软件可对励磁线圈损耗进行较准确计算的前提下，通过仿真计算得到空载及负载工况条件下的励磁线圈损耗差，并对传统测量方法得到实验结果进行修正，可以得到更准确P21基准模型的导磁构件损耗。

(2)更准确的导磁构件损耗有助于仿真计算方法的优化及提高仿真计算结果的准确性。

(3)本方法适用于P21基准问题中含导磁构件的模型，对于非导磁构件，如铜板、非导磁钢板等，由于空、负载工况条件下的漏磁场分布差别很小，且构件损耗较小，不需用本方法再作处理得到构件损耗。

[1]程志光，刘涛，范亚娜，等.基于TEAM P21三维杂散场问题建模仿真与验证 [J]. 电工技术学报，2014, 29(9):194-203.

[2]CHENG Z, TAKAHASHI N, FORGHANI B, et al. Extended progress in TEAM problem 21 family[J]. COMPEL, 2014, 33(1/2): 234-244.

[3]IEEE Std 1597.1TM-2008: IEEE Standard for validation of computational electromagnetics computer modeling and simulations[S]. 2008

[4]程志光，高桥泽雄，博札德·弗甘尼，等.电气工程电磁热场模拟与应用 [M]. 北京：科学出版社，2009.

[5]范亚娜，张卫东，程志光,等.基于不同B-H曲线的取向硅钢叠片中损耗和磁通的分析与验证[J]. 华北电力大学学报(自然科学版)，2011, 38(4)：8-12.

[6]CHENG Z, TAKAHASHI N, FORGHANI B, et al. 3-D finite element modeling and validation of power frequency multi-shielding effect[J]. IEEE Transactions Magnetics, 2012, 48(2): 243-246.

[7]CHENG Z, TAKAHASHI N, FORGHANI B, et al. Analysis and measurements of iron loss and flux inside silicon steel laminations[J]. IEEE Transactions Magnetics, 2009, 45(3):1222-1225.

[8]程志光，胡启凡，高桥则雄，等. 国际TEAM Problem 21基准族及工程涡流问题模拟[J]. 中国工程科学, 2007, 9(7):38-46.

[9]范亚娜，刘洋，马光，等.电力变压器两种磁屏蔽中磁通及损耗的仿真分析与验证[J]. 电工电能新技术，2015, 34 (7)：32-36.

[10]赵小军，李琳，程志光，等. 基于直流偏磁实验的叠片铁心磁化特性分析[J]. 电工技术学报，2011,26(1):7-13.

[11]ZHANG Y, PENG Z, XIE D, et al. Effect of different magnetization curves on simulation for transformer core loss under DC bias[J]. Transactions, China Electrotechnical Society, 2014,29(5):43-48.

[12]CHENG Z, TAKAHASHI N, FORGHANI B, et al. Modeling of magnetic properties of GO electrical steel based on Epstein combination and loss data weighted processing[J]. IEEE Transactions Magnetics,2014,50(1):1-9.

[13]CHENG Z, TAKAHASHI N, FORGHANI B, et al. Effect of variation of B-H properties on loss and flux inside silicon steel lamination[J]. IEEE Transactions Magnetics, 2011,47(5):1346-1349.

[14]ZHENG W, CHENG Z. Efficient finite element simulation for GO silicon steel laminations using inner-constrained laminar seperation[J]. IEEE Transactions on Magnetics, 2012, 48(8):2277- 2283.

[15]CHENG Z, TAKAHASHI N, FORGHANI B, et al. Effect of excitation patterns on both iron loss and flux in solid and laminated steel configurations[J]. IEEE Transactions Magnetics, 2010,46(8):3185-3188.

Research and Verification of Stray Loss Measurement Method Based on TEAM P21 Benchmark Model

LIU Tao1， LIU Lanrong1， ZHANG Junjie1， NIE Jingkai2， CHENG Zhiguang1， JIN Wende3

(1. Baoding Tianwei Baobian Electric Co. Ltd.,Baoding 071056,China;2. Global Energy Interconnection Research Institute, Beijing 102211, China;3. State Grid Zhejiang Electric Power Company, Hangzhou 310007, China)

Based on TEAM P21 benchmark model, combined with electromagnetic simulation software, the stray losses of magnetic components under different frequencies are studied by experiments and simulation. In the TEAM P21 benchmark problems, the leakage flux produced by magnetic components will bring influence on the exciting coil, so the traditional method of load (coil and magnetic component) subtracting no-load (exciting coil) loss to measure the magnetic component loss will bring a certain error. To avoid this error, a new method of measuring magnetic component loss is proposed. On the premise that the exciting coil(copper coil, linear material) loss can be calculated accurately by simulation, the loss difference of the excitation coil under no-load and load conditions is obtained, which can be used to correct the experimental results. The measurement method and experimental data obtained through the method can help to obtain more accurate results of stray losses of magnetic components and furtherly improve the simulation accuracy.

TEAM P21 benchmark problem; leakage magnetic flux; stray loss; silicon steel lamination

2017-08-20。

国家电网公司科技项目(SGRIDGKJ[2015]212)。

10.3969/j.ISSN.1672-0792.2017.12.011

TM275

A

1672-0792(2017)12-0061-06

刘涛(1984-)，男，工学硕士，工程师，研究方向为工程电磁场分析与实验，磁性材料模拟与应用。