北斗三频海基JPALS无故障导航算法
2018-01-05王官龙崔晓伟陆明泉
王官龙,崔晓伟,陆明泉
清华大学 电子工程系,北京 100084
北斗三频海基JPALS无故障导航算法
王官龙,崔晓伟*,陆明泉
清华大学 电子工程系,北京 100084
基于卫星导航系统的海基精密进近与着陆系统(JPALS)是未来舰载机自主着舰引导技术的发展方向。针对当前海基JPALS导航算法的研究都是基于双频观测量,存在无几何滤波时间长、要求的伪距观测量精度较苛刻的问题,提出一种在北斗(BDS)海基JPALS中使用三频观测量的无故障导航算法。通过对在中国东海钓鱼岛海域7天时间使用该导航算法用于精密进近引导的性能进行仿真分析,结果表明:该北斗海基JPALS无故障导航算法使用B1/B2宽巷和B1/B3中巷组合的无几何模糊度预滤波架构只需要8 min无几何滤波时间就能实现海基JPALS要求的性能,而且其对伪距观测量的精度要求甚至可以放宽到50 cm,使北斗海基JPALS的可用性性能大大提高。此外,载波相位观测量精度不能超过0.7 cm时,该北斗三频海基JPALS算法能在3 n mile外就实现模糊度固定,使高精度载波相位提早用于海基JPALS精密进近引导。
海基JPALS;北斗;三频;无几何预滤波;观测量精度
美国海军基于GPS差分载波相位相对定位技术发展的海基精密进近与着陆系统(Sea-Based Joint Precision Approach and Landing System, SB-JPALS),实现了舰载机在极端气象条件和复杂电磁环境下自动引导着舰,极大提高了着舰效率和安全性。为保证着舰安全,海基JPALS对定位精度、完好性、连续性、可用性都提出了很高的要求:完好性风险<1×10-7,垂直告警限(Vertical Alert Limit,VAL)<1.1 m,可用性>0.997[1]。
海基JPALS使用载波相位作为观测量实现高精度定位,首先必须在飞行中可靠地解决模糊度固定问题[2]。美国为其设计了一种使用GPS双频观测量的无故障导航算法架构,其算法的实现过程可分为前后紧密相联的两个阶段:第1阶段是在舰载机接近航母前,舰载海基JPALS计算机和航母海基JPALS参考站处理系统分别独立地进行无几何的非差宽巷(Wide-Lane, WL)模糊度低通滤波处理,估计出高精度的无几何非差宽巷模糊度的浮点值及其方差;第2阶段是在舰载机接近航母(距离小于0.25 n mile)时,舰载海基JPALS计算机在本地联合收到航母海基JPALS参考站观测数据,组成双差相对定位观测方程,几何冗余固定模糊度,求解相对位置向量[3-4],估计定位完好性和可用性。在载波相对定位中,为提高第2阶段的相对位置向量估计精度,应尽可能多地固定模糊度整数值,但为保证定位误差满足系统完好性风险要求,几何冗余模糊度的错误固定概率又必须小于设定的数值,这些需求对当前的北斗(BDS)实际伪距(33 cm[5])和载波相位测量值精度来说,第1阶段的无几何低通滤波大约需要15 min以上的连续时间[6-7]。一旦在无几何滤波过程中,因舰载机高动态、严重的多径、干扰等导致信号失锁,发生周跳,则整个预滤波过程就可能要重启,这严重威胁海基JPALS第2阶段的几何冗余算法可用性。
当前,北斗系统为授权用户提供3个频率的导航信号,三频观测量不仅对飞行中可靠的周跳检测有极大优势[8],而且能提供更多的冗余观测量,明显增强海基JPALS的接收机自主完好性监测(RAIM)能力[9]。本文在参考GPS 海基JPALS双频导航算法架构的基础上[6],将其无故障导航算法的处理思路拓展到使用北斗三频信号,设计了一种新的基于北斗三频观测量的海基JPALS无故障导航算法。通过在中国东海海域,对北斗海基JPALS精密进近引导性能仿真结果显示:与北斗双频导航算法架构相比,在相同的载波相位测量精度下,使用北斗三频算法架构能明显缩短需要的无几何低通滤波时间,放宽对伪距测量精度要求,极大地提高了系统可用性;而且该三频海基JPALS算法能在距离航母3 n mile就实现模糊度固定,使高精度载波相位观测量提早用于故障检测,极大地提高了载波相位观测量的使用效率。此外,该三频海基JPALS算法应用非常灵活,在北斗某一频点存在干扰无法使用时,能自动退化到使用双频观测量的算法架构,具有极强的系统鲁棒性。通过本文的研究,可为将来中国发展基于北斗系统的海基JPALS的算法选择提供参考。
1 算法数学模型
北斗三频海基JPALS导航算法基本处理思路采用与双频架构相似的两阶段导航算法。该两阶段无故障导航算法的成功基础是第1阶段的无几何组合模糊度低通滤波处理,为保证第2阶段的相对定位结果完好性,一般要求几何冗余模糊度错误固定概率小于系统整体的完好性风险概率一个数量级,本文中设定允许的最大模糊度错误固定概率为1×10-8[2]。
1.1 无几何低通滤波处理
北斗3个频率的观测量可以低通滤波估计出3组无几何的非差组合模糊度浮点值及其方差,分别是:B1/B2宽巷,B1/B3中巷(Medium Lane,ML),B2/B3超宽巷(Extra Wide Lane,EWL)。这里以北斗B1/B3中巷组合为例说明北斗海基JPALS的无几何非差模糊度低通滤波处理过程。
用户对北斗卫星i的B1、B3双频载波相位联合伪距观测量计算无几何非差组合模糊度浮点值的过程为[6]
(1)
(2)
第1阶段的无几何非差中巷模糊度低通滤波处理在舰载机和航母参考站分别独立进行[2],分别得到各自的无几何中巷模糊度浮点估计值及其方差。在舰载机进入航母参考站数据链路服务范围后[2],开始激活第2阶段的相对位置求解处理过程。
1.2 三频海基JPALS几何冗余相对定位算法
当机载海基JPALS计算机收到数据链路发送来的航母海基JPALS参考站低通滤波处理得到的无几何模糊度浮点值和方差,以及原始载波相位观测量后,就可以对本地和参考站的无几何中巷模糊度浮点值做双差处理,消除残留的频间偏差[1],对本地和参考站相同时间标的载波相位观测量作双差处理,消除观测量中的卫星和本地钟差误差、电离层延迟和对流层延迟误差、频间偏差和星历误差[10],然后开始相对定位计算。
海基JPALS使用北斗三频观测量,可以低通滤波处理得到无几何的北斗宽巷、中巷和超宽巷3个组合模糊度的浮点值和其方差,将3个无几何组合模糊度计算的双差值表示为单频双差模糊度相减的形式,如式(3)~式(5)所示[1,11]。三频载波相位双差相对定位的数学表达式如式(6)~式(8)所示[10]。
(3)
(4)
(5)
(6)
(7)
(8)
式(3)~式(5)的3个无几何组合模糊度中,有2个无几何模糊度是不相关的[10],从中取2个双差模糊度方程,联合式(6)~式(8)的载波相位双差相对定位方程组成北斗三频海基JPALS的无故障导航算法数学方程[1,4,11]。这样依据选取的双差模糊度的组合不同,有3种形式的三频海基JPALS无故障导航算法可用,分别是:宽巷和中巷组合三频算法、中巷和超宽巷组合三频算法、宽巷和超宽巷组合三频算法。经过仿真分析,宽巷和中巷组合三频海基JPALS无故障导航算法具有最好的应用性能,因此这里只给出该三频海基JPALS无故障导航算法的相对定位数学方程,对所有可用卫星(假设在舰载机和航母间共有n颗可用卫星)的双差方程进行联合处理,表示为矩阵形式
(9)
式中:G为(n-1)×3的双差相对定位几何观测矩阵;I为(n-1)×(n-1)的单位矩阵。将式(9)简化为
z=Hx+v
(10)

(11)
(12)
(13)
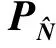

(14)
式中:Kffd为与系统完好性风险(1×10-7)一致的完好性乘数,为5.33。当VPL 北斗三频海基JPALS无故障导航算法在处理过程中,如果某一频点由于存在干扰或故障而不可用,该三频算法可以自动切换到北斗双频海基JPALS算法,从而保持整个精密进近引导过程的连续性和可用性。这里假设北斗B2频点不可用,则式(9)的三频海基JPALS无故障导航算法方程变为 (15) 而其观测量误差协方差矩阵变为 (16) 双频算法的状态向量求解、模糊度整数固定、位置向量及误差方差的更新计算、性能评估与三频算法一致。 对本文设计的北斗三频海基JPALS导航算法性能进行仿真分析,评估其对伪距、载波相位观测量精度,以及预滤波时间的需求。 在舰载机海基JPALS计算机和航母参考站海基JPALS计算机处分别使用一阶马尔可夫随机过程仿真对式(1)计算的无几何非差中巷模糊度进行低通滤波处理,该低通滤波处理过程可模型化为一阶马尔可夫随机过程,滤波后的无几何模糊度方差可表示为[4] (17) (18) 图1 无几何模糊度预滤波仿真1.3 有单频干扰时的切换算法
2 仿真分析
2.1 无几何模糊度滤波

Fig.1 Geometric-free ambiguity pre-filtering simulation
实际观测数据统计的舰载机和航母接收机多径误差自相关常数为5 s和60 s[1],为方便仿真分析,这里将舰载机和航母无几何低通滤波的观测量多径误差自相关常数统一设为60 s[2]。图1是对该无几何低通滤波过程中对北斗B1/B3中巷模糊度在载波相位精度0.7 cm时的仿真结果。图中棕色虚线是在有8颗卫星所要求整体的模糊度错误固定概率低于1×10-8时,要求的中巷模糊度误差标准差应低于0.08周。
从图1中看到,在当前北斗伪距观测量精度为33 cm时[5],所需要的预滤波时间将近20 min,这一预滤波时间长度要求可在第2阶段的几何冗余模糊度固定方法中压缩。
2.2 三频海基JPALS观测量精度要求
使用式(13)给出低通滤波后模糊度浮点值方差,则其双差模糊度协方差矩阵为
(19)
(20)
图2 北斗三频海基JPALS算法观测量精度
Fig.2 Measurements accuracy for BDS triple-frequency sea-based JPALS
为降低仿真复杂度,合理的设定仿真中在舰载机和航母参考站有相同的观测量精度、滤波时间[2]。图2是在8 min(包括无几何滤波时间和几何冗余定位时间,因几何冗余定位处理时间很短,只有十几秒,因此本文统称为无几何低通滤波时间)无几何滤波时间下使用北斗三频海基JPALS宽巷和中巷组合算法、中巷和超宽巷组合算法、宽巷和超宽巷组合算法的伪距和载波相位观测量精度仿真结果。从图2看到,在北斗三频海基JPALS无故障导航算法中:① 宽巷和中巷组合算法性能最好,对伪距测量精度的要求最宽,载波相位测量精度0.7 cm时(实际测量中,高精度接收机对载波相位跟踪精度可达到0.01周,换算为长度大约为0.2 cm,如果加上使用阵列天线引入0.01~0.02周的误差和从接收机天线到舰载机起落架的换算误差,总的载波相位误差为0.6 cm,因此0.7 cm载波相位精度设定能够满足北斗海基JPALS实际使用需求)[1],伪距精度要求可放宽到40 cm(对应实测伪距精度为33 cm)[5];② 宽巷和超宽巷组合算法的性能最差,8 min的滤波时间不足以固定足够数量的模糊度,不宜在北斗三频海基JPALS算法中采用;③ 中巷和超宽巷组合算法的性能居中,当前的伪距测量精度能够满足其要求。综上所述,北斗三频海基JPALS无故障导航算法应采用宽巷和中巷组合的无几何模糊度滤波算法。
2.3 三频海基JPALS精密进近性能
将2.2节仿真分析得到的满足海基JPALS性能需求的北斗三频观测量精度和滤波时间数据,用于海基JPALS的精密进近性能仿真。
舰载机从决定返航开始,在距离航母大约为15 n mile时,进入航母战术空中导航系统服务范围,在距离航母3 n mile时,航母自动着舰系统引导操作启动,大约0.5 n mile时,航母光学助降系统开始工作,舰载机据此下滑着舰[18-20]。依据典型的舰载机引导着舰过程,特将北斗海基JPALS的舰载机引导精密进近着舰过程模型化为如下过程[16]:① 舰载机在距离航母20 n mile外开启舰载海基JPALS处理计算机,开始进行无几何模糊度低通滤波处理,使得到最后着舰,大约有8 min以上的无几何模糊度滤波时间;② 在距离航母3 n mile处开启海基JPALS精密进近引导操作处理,包括组成三频载波相位双差相对定位观测方程、联合宽巷和中巷无几何模糊度、固定满足海基JPALS完好性风险要求的部分单频模糊度整数、解算舰载机相对航母的相对位置、计算完好性风险和可用性(为说明北斗三频海基JPALS定位引导质量,仿真中在精密进近中每一个点都进行几何冗余的相对位置解算、完好性计算和可用性判断等处理);③ 在精密进近引导操作过程中,设定舰载机沿3°迎角直线下滑着舰,且一直保持140 n mile/h的速度不变,直到舰载机接触航母触舰点。
精密进近仿真分析条件的设置大致与北斗三频海基JPALS的观测量精度性能要求仿真处理一致,除了将仿真间隔调整为10 min进行一次精密进近引导仿真,相对定位频率1 Hz,在7天的仿真时间内共有1 008条精密进近引导操作下滑线。
图3 北斗三频海基JPALS精密进近引导性能
Fig.3Performance of precise approach for BDS triple-frequency SB -JPALS
图3采用宽巷和中巷组合对无几何模糊度进行低通滤波处理,预滤波时间8 min时的北斗三频海基JPALS无故障导航算法的精密进近引导性能仿真结果。其中,为以更加形象的方式说明北斗观测量(伪距和载波相位)精度对北斗三频海基JPALS引导质量的影响,图3中同时给出了3种观测量精度时,海基JPALS精密进行引导质量曲线。其中红色实线是海基JPALS引导质量要求的VAL[16]。
图3中,为了更清晰地显示北斗三频海基JPALS的引导质量,这里情况1(蓝线)为精密进近仿真曲线中VPL最大的一条,看到在伪距测量精度40 cm,载波相位测量精度0.7 cm的观测量精度下,北斗三频海基JPALS精密进近引导可用性达到100%。情况2(绿线)为所有在精密进近仿真曲线中VPL有超过VAL的曲线,从图3中看到只在距离航母0.25 n mile左右的引导性能不能满足海基JPAS要求,但是在0.2 n mile以内的引导性能完全满足海基JPALS引导质量要求,整体的导航可用性达到99.89%,符合海基JPALS可用性要求。情况3(青色线)中,从右开始VPL值等于VAL的情形表示精密进近仿真中模糊度整数固定达不到完好性风险要求阶段,这里也只画出了所有模糊度达不到固定要求的曲线,看到:将载波相位测量精度放宽到0.8 cm,系统的可用性急剧降低,满足几何冗余模糊度固定概率要求的可用性只有17%,即使载波相位测量精度为0.75 cm时,满足几何冗余模糊度固定概率要求的可用性也只有97%,说明北斗三频海基JPALS采用宽巷和中巷无几何模糊度组合的无故障导航算法载波相位观测量精度不宜超过0.7 cm。
在北斗三频海基JPALS某一频点不可用时,该三频算法自动转化为双频海基JPALS导航算法,对北斗双频海基JPALS算法的精密进近引导性能进行仿真分析,仿真条件的设定与三频算法精密进近引导仿真一致,图4为北斗双频海基JPALS无故障导航算法精密进近引导性能仿真结果。北斗三频海基JPALS转化为双频海基JPALS有3种情况:情况1是在B3频点不可用时,转化为B1/B2宽巷双频海基JPALS,设定要求的伪距测量精度为35 cm,载波相位测量精度为0.8 cm,无几何滤波时间为13 min,系统可用性能达到99.72%,且在0.1 n mile内的精密进近引导性能全部满足海基JPALS要求,仿真结果如图4(a)绿色线所示;情况2是在北斗B2频点不可用时,三频海基JPALS算法转化为B1/B3中巷双频算法,在设定伪距测量精度为35 cm,载波相位测量精度为0.7 cm,无几何滤波时间为13 min时,系统的可用性达到99.86%,且在0.25 n mile内精密进近引导性能全部满足海基JPALS要求,仿真结果如图4(a)蓝色线所示(其中,为清晰显示北斗双频海基JPALS精密引导性能,这里只给出了精密进近中VPL有超过VAL情况的曲线);情况3是在北斗B1频点不可用时,B2/B3超宽巷模糊度虽然波长较长,超宽巷模糊度整数值较容易固定(距离航母10 n mile就可固定超宽巷模糊度),但是超宽巷双频算法并不能满足海基JPALS的最后精密进近阶段的精度要求,图4(b)为无几何滤波时间为10 min,伪距精度为40 cm,载波相位测量精度为0.5 cm时的北斗超宽巷海基JPALS精密进近引导质量曲线。
图4 北斗双频海基JPALS精密进近引导性能
Fig.4Performance of precise approach for BDS dual-frequency SB -JPALS
在图4(a)的北斗宽巷和中巷双频海基JPALS算法中,如继续放宽对载波相位的测量精度,将不能满足海基JPALS可用性要求,而放宽伪距精度要求就必须增加无几何滤波时间。对于北斗B1频点不可用的北斗超宽巷海基JPALS算法,即使加长滤波时间,一般只能固定3~4颗卫星的单频模糊度,导致定位算法的卫星空间几何较差,且故障检测能力也不强,因此先滤波后固定模糊度的两阶段海基JPALS导航算法思路并不适合,需要研究新的导航算法架构,一种可行的方法是借鉴民航的单频精密进近引导算法,但也存在需要较长时间模糊度固定和有几何定位可靠性不高问题,这一问题是下一阶段海基JPALS算法研究的方向。
3 结 论
对北斗海基JPALS使用三频观测量的无故障导航算法进行了研究。在给出该相应算法的数学方程及观测量协方差矩阵后,使用仿真分析方法,对该方法在中国东海钓鱼岛海域的海基JPALS精密进近引导性能进行了评估。结果显示:
1) 北斗三频海基JPALS在伪距观测量精度为40 cm,载波相位测量精度为0.7 cm时,只需要8 min无几何滤波时间,能完全满足海基JPALS在3 n mile内的精密进近引导质量性能需求,即使将伪距测量精度要求放宽到50 cm,也能满足距离航母0.2 n mile内的海基JPALS性能需求,但是该三频算法使用的限制条件是载波相位测量精度不能超过0.7 cm,否则将不能满足完好性风险要求的模糊度正确固定概率。
2) 北斗海基JPALS三频算法相比双频算法,能明显缩短需要的无几何低通滤波时间,放宽对伪距测量精度要求,极大的提高北斗海基JPALS的可用性。
需要说明的是,本文使用仿真分析方法验证了北斗三频海基JPALS的良好性能,本文对观测量误差作了简化处理,只基于常见误差源给出了统一的观测量精度要求,而海基JPALS的实际工程应用环境非常复杂,还存在射频干扰、天线相位中心变化、载体运动引起的天线旋转偏差、参考站测量值位置转换误差、为抗干扰使用阵列天线引入的误差等没有单独给出误差精度模型。因此,以后的北斗海基JPALS工程发展中,还需要对实际环境中上述多种观测误差进行研究、评估,进行建模分析,给出符合实际使用环境的观测量精度模型,保证系统的实用性。同时,北斗是一个包含地球同步轨道(GEO)、倾斜地球同步轨道(IGSO)和MEO 3类卫星的异构导航星座,3种卫星由于相对用户的空间几何变化速度不同,导致海基JPALS使用的最优无几何滤波时间在不同类型卫星间是不同的,如何更好地利用北斗特殊星座的优势,提高其在海基JPALS完好性、可用性性能是以后北斗海基JPALS的重要研究方向。
[1] RIFE J, KHANAFSEH S, PULLEN S, et al. Navigation, interference suppression, and fault monitoring in the sea-based joint precision approach and landing system[J]. Proceedings of the IEEE, 2009, 96(12): 1958-1975.
[2] HEO M B. Robust carrier phase DGPS navigation for shipboard landing of aircraft[D]. Chicago, IL: Illinois Institute of Technology, 2004: 94-120.
[3] DOGRA S, WRIGHT J, HANSEN J. Sea-based JPALS relative navigation algorithm development[C]∥Proceed-ings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation. Long Beach, CA: ION Publications, 2001: 2871-2881.
[4] KHANAFSEH S M, PERVAN B. Autonomous airborne refueling of unmanned air vehicles using the global positioning system[J]. Journal of Aircraft. 2015, 44(5): 1670-1682.
[5] 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学(地球科学), 2014, 44(1): 72-81.
YANG Y X, LI J L, WANG A B, et al. Preliminary assessment of the navigation and positioning performance of Beidou regional navigation satellite system[J]. Science China (Earth Sciences), 2014, 44(1): 72-81 (in Chinese).
[6] HEO M B, PERVAN B. Carrier phase navigation architecture for shipboard relative GPS[J]. IEEE Transactions on Aerospace & Electronic Systems, 2006, 42(2): 670-679.
[7] WANG G, CUI X, LU M. The analysis of availability and integrity for Beidou-based high precise KINRTK[C]∥China Satellite Navigation Conference (CSNC) 2016 Proceedings. Beijing: CSNC, 2016: 189-198.
[8] 黄令勇, 翟国君, 欧阳永忠, 等. 三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717-725.
HUANG L Y, ZHEN G J, OUYANG Y Z, et al. Ionospheric cycle slip processing in triple-frequency GNSS[J]. Acta Geodaeticaet Cartographica Sinica, 2015, 44(7): 717-725 (in Chinese).
[9] 郭婧, 陆明泉, 崔晓伟, 等. 三频GNSS接收机的RAIM算法研究[J]. 宇航学报, 2011, 32(8): 1734-1739.
GUO J, LU M Q, CUI X W, et al. Research on RAIM algorithm for triple-frequency GNSS receiver[J]. Journal of Astronautics, 2011, 32(8): 1734-1739 (in Chinese).
[10] MISRA P, ENGE P. Global positioning system: Signals, measurements and performance[M]. 2nd ed. Lincoln, MA: Ganga-Jamuna Press, 2006: 112-158.
[11] KHANAFSEH S M. GPS navigation algorithms for autonomous airborne refueling of unmanned air vehicles[J]. Dissertations&Theses-Gradworks, 2008, 44(5): 1670-1682.
[12] 谢刚. GPS 原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 97-108.
XIE G. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2009: 97-108 (in Chinese).
[13] TEUNISSEN P, DE JONGE P J, TIBERIUS C. The least-squares ambiguity decorrelation adjustment: Its performance on short GPS baselines and short observation spans[J]. Journal of Geodesy. 1997, 71(10): 589-602.
[14] TEUNISSEN P J G. GNSS ambiguity bootstrapping: Theory and application[C]∥Proceedings of International Symposium on Kinematic Systems in Ceodesy, Geomatics and Navigation. Banff, Canada: KIS, 2001: 246-254.
[15] KHANAFSEH S, PERVAN B. New approach for calculating position domain integrity risk for cycle resolution in carrier phase navigation systems[J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(1): 296-307.
[16] JOERGER M, STEVANOVIC S, KHANAFSEH S, et al. Differential RAIM and relative RAIM for orbit ephemeris fault detection[C]∥Position Location and Navigation Symposium. Piscataway, NJ: IEEE Press, 2012: 174-187.
[17] MCGRAW G A, MURPHY T, BRENNER M, et al. Development of the LAAS accuracy models[C]∥Praeedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation. Long Beach, CA: ION Publications, 2000: 1212-1223.
[18] 小飞猪. 中国航母.着舰之难.专题报道[J]. 现代舰船, 2012(8): 14-21.
XIAO F Z. Special report about approach and land at aircraft carrier of China[J]. Modern Ships Magazine. 2012(8): 14-21 (in Chinese).
[19] 佚名. 归家的明灯——浅谈舰载机着舰下滑引导系统[EB/OL]. (2014-01-25)[2017-04-29]. 哈尔滨工程大学“三海一核”科普网. http:∥uzone.univs.cn/ news2_2008_545572.html.
ANOM. The lights to home, talking about the automatic carrier landing system[EB/OL].(2014-01-25)[2017-04-29]“Three Sea and One Nuclear” popular science of Harbin Engineering University. http:∥uzone.univs.cn/news2_2008_545572.html (in Chinese).
[20] 陈彩辉, 周荣坤, 吴红兵. 基于机舰协同的舰载机着舰过程分析[J]. 电脑与信息技术, 2010, 18(4): 8-10.
CHEN C W, ZHOU R K, WU H B. Analyse of landing process of air wings based on cooperation with the carrier[J]. Computer and Information Technology, 2010, 18(4): 8-10 (in Chinese).
Triple-frequencysea-basedJPALSfault-freenavigationalgorithmforBDS
WANGGuanlong1,*,CUIXiaowei1,LUMingquan1
DepartmentofElectronicEngineering,TsinghuaUniversity,Beijing100084,China
Basedonthenavigationsatellitesystem,sea-basedJointPrecisionApproachandLandingSystem(JPALS)representsthedirectionoffuturedevelopmentoftheshipboardaircraftauto-landingtechnology.Thecurrentresearchesonsea-basedJPALSnavigationalgorithmisbasedondual-frequencymeasurements,whichhastheproblemoflonggeometric-freefilteringperiodandstringentrequirementoftheaccuracyofpseudo-rangemeasurements.Sointhisdissertation,prototypealgorithmsforsea-basedJPALSbasedontriple-frequencymeasurementsofBeidouNavigationSatelliteSystem(BDS)isproposed.Theresultsof7dayssimulationanalysisatseaareaofChinaDiaoyuislandsshowthatitonlytakes8minofgeometric-freefilteringtimeforthisthree-frequencynavigationalgorithmtoachievetherequiredperformanceofsea-basedJPALSbyusingtheB1/B2Wide-LaneandB1/B3Medium-Lanecombinationfortriple-frequencygeometric-freeambiguitypre-filteringalgorithm.AndtheavailabilityperformanceofBDStriple-frequencysea-basedJPALScanbeenhancedgreatlyeveniftheaccuracyofpseudo-rangemeasurementsisrelaxedtoasmuchas50cm.AndanotheradvantageofthisBDStriple-frequencysea-basedJPALSalgorithmis,whentheaccuracyofthecarrierphasemeasurementsiswithin0.7cm,itcanfixtheambiguityat3nmileawayfromtheaircraftcarrier,whichleadstotheearlierapplicationofhighprecisioncarrierphasemeasurementstotheBDSsea-basedJPALSintegritymonitoring.
sea-basedJPALS;BeidouNavigationSatelliteSystem(BDS);triple-frequency;geometric-freepre-filtering;measurementsaccuracy
2017-04-21;
2017-05-15;
2017-07-18;Publishedonline2017-08-021601
URL:http://hkxb.buaa.edu.cn/CN/html/20171225.html
.E-mailcxw2005@tsinghua.edu.cn
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2017.321340
2017-04-21;退修日期2017-05-15;录用日期2017-07-18;网络出版时间2017-08-021601
http://hkxb.buaa.edu.cn/CN/html/20171225.html
.E-mailcxw2005@tsinghua.edu.cn
王官龙,崔晓伟,陆明泉.北斗三频海基JPALS无故障导航算法J. 航空学报,2017,38(12):321340.WANGGL,CUIXW,LUMQ.Triple-frequencysea-basedJPALSfault-freenavigationalgorithmforBDSJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):321340
V474.2
A
1000-6893(2017)12-321340-09
苏磊, 李丹)
