基于有理插值函数的GM(1,1)模型背景值重构

康 宁，张静静，李晓莹

（阜阳师范学院 经济学院，安徽 阜阳 236037）

基于有理插值函数的GM(1,1)模型背景值重构

康 宁，张静静，李晓莹

（阜阳师范学院 经济学院，安徽 阜阳 236037）

基于有理插值函数的方法，提出了一类新的灰色预测模型RIGM(1,1)，改进了原有模型中背景值的构造方法，克服了现有GM(1,1)模型的不足，为提高预测精度提供了新的途径。较之其他方法，具有较高的预测精度和较小的计算量。最后以中国总消费的数据为例，验证了本方法的有效性。

有理插值；背景值；GM(1,1)模型；预测精度

灰色预测法是一种对既含有已知信息又含有不确定因素的系统进行预测的方法，即对在一定范围内的、与时间有关的灰色过程进行预测。尽管灰色系统中所显示的现象是随机的，但这一数据集合具备潜在的规律。灰色预测方法的思想是：对原始时间序列进行一次累加运算，生成新的具有较强规律的时间序列；然后，建立相应的微分方程模型，进而利用差分法对原方程进行离散化得到一个线性方程组；最后，利用回归法对未知参数进行辨识，从而得到预测模型。

GM(1,1)模型是灰色预测法的基本模型，也是应用最广泛的模型。利用GM(1,1)模型进行预测虽然有许多成功的实例，例如，文献[1]基于周期截断积累与修正项，提出了一种离散的GM(1,1)模型，提高了季节性时装零售预测的准确性；文献[2]利用三次样条函数和粒子群（PSO）算法优化的GM(1,1)模型分析了日本的固定电话和手机需求问题，实验结果表明所提出的新模型具有良好的性能；但也存在一些预测结果不理想的情况，反映出GM(1,1)模型的实用性有待进一步提高。自灰色预测模型建立以来，为了适应各应用领域的特点，GM(1,1)模型在初始条件选取、背景值重构、参数辨识方法等方面都取得了很大改进。文献[3]给出一种新的背景值构造方法；提高了模型的预测精度；文献[4]研究了模型的适用范围；文献[5]根据差分进化算法优化模型的参数，并提高了预测精度；文献[6]通过优化初始条件，提高了模型的预测精度；文献[7]利用线性微分方程的解来构造背景值，在一定程度上提高了模型的精度；文献[8]利用Lagrange插值方法对原有模型的背景值进行了改进；文献[9]利用Newton-Cores公式改进了背景值，并提高了模型的预测精度；文献[10]利用数乘变换来解决GM(1,1)模型的病态性问题；文献[11-12]从矩阵的扰动理论出发，利用累积法来解决GM(1,1)模型的病态性问题。上述方法虽然很好，但其缺陷在于：数乘变换法没有给出降低系数矩阵条件数的具体准则；累积法所得到的结论与新信息优先的原理相矛盾，且累计阶数如何选取并没有解决。

由文献[13]可知，GM(1,1)模型的预测精度主要由背景值重构的质量所决定的，背景值的构造方法将直接影响到模型的预测精度和适用性。最近研究结果表明，采用插值算法构造背景值效果明显。但现有构造背景值的插值算法，都存在一定的局限性，例如文献[8]的Lagrange插值和文献[9]的Newton插值片面追求精度，而导致Runge现象的出现，预测模型的预测结果失真。文献[13-14]分别提出组合插值和三次样条插值的方法构造背景值，取得了很好的结果。

本文利用有理插值的方法，构造出一种有理插值函数r(x)，使其在区间[k,k+1]上的积分去替代背景值z(1)(k+1)。较之其他方法，具有预测精度高、计算量小等优点。

1 模型的建立

1.1 传统的GM(1,1)模型

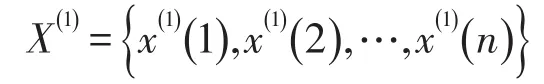
称一阶线性微分方程：

为GM(1,1)模型的白化微分方程，其差分形式

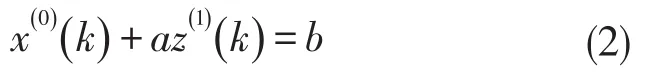
其中a,b为待辨识参数，且称a为发展系数，反映x(0)及x(1)的发展态势；b为灰色作用量，具有灰色信息覆盖的作用，不能直接观测，只能通过计算得到。由最小二乘法求解得

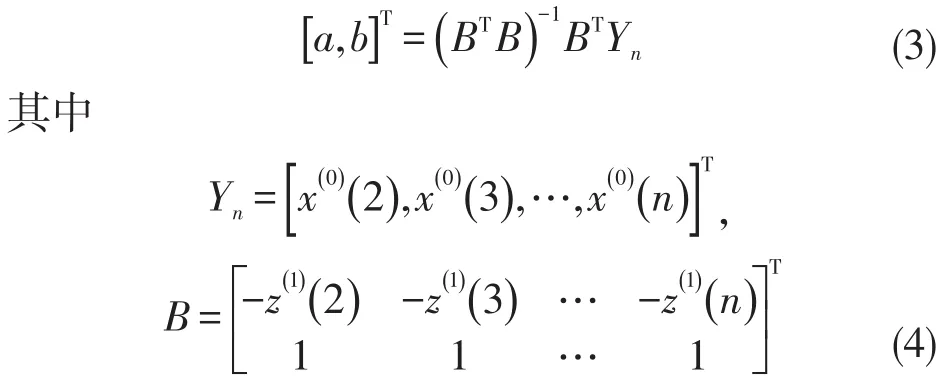
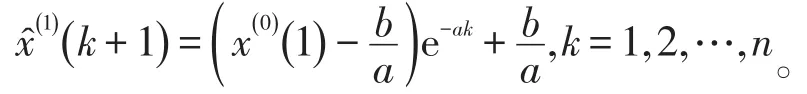
累减还原得GM(1,1)的预测模型为：

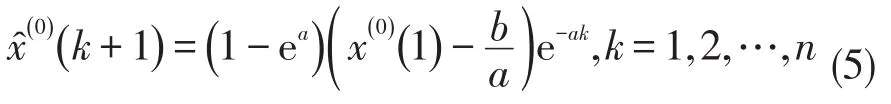
1.2 有理插值的背景值构造

由传统GM(1,1)模型的建模过程，可以发现，模型的发展系数a和灰色作用量b对模型的预测精度具有深刻的影响，但a,b的取值取决于背景值的构造。传统模型的背景值实质上利用梯形公式计算出x(1)(t)在区间[k,k+1]上的积分代替背景值z(1)(k+1)；根据文献[15]可知梯形积分公式的代数精度很低，从而导致模型预测偏差较大，在一定程度上影响了模型的适用性。因此，本文利用一种有理插值算法，构造出了一种新的背景值，它不仅具有已有模型的优点，而且又提高模型预测精度和适用性。

下面介绍插值的一些概念与定理：

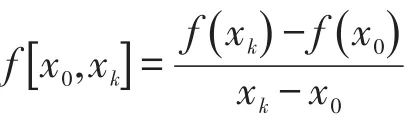
一般地，称

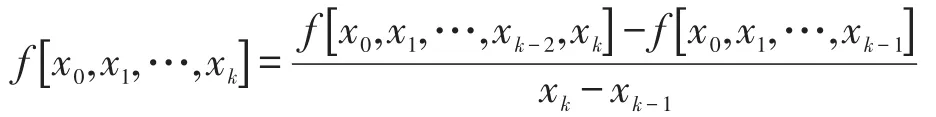
为f(x)的k阶差商。

定义2[15]称形如下式的插值Nn(x)

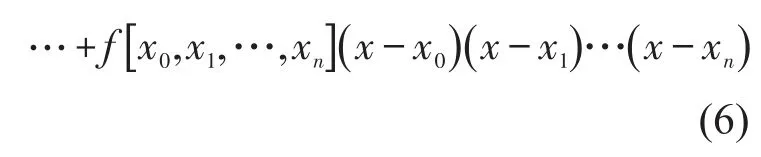
为Newton插值多项式。

定义3[16]给定n+1个互异的点

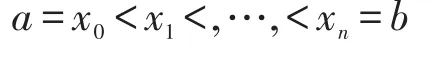
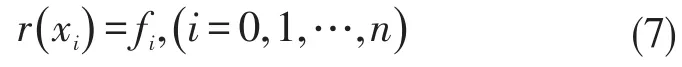
引理1[17]对任意给定的正整数m(1≤m≤n),由式（8）所确定的有理函数r(x)是满足插值条件r(xi)=fi,(i=0,1,…,n)

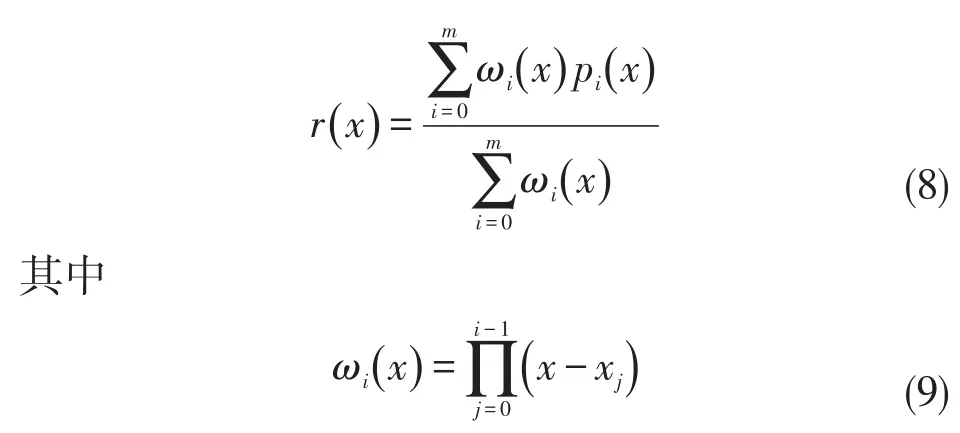
pi(x)表示在点xi,xi+1,…,xn上的Newton插值多项式，根据定义2可得其表达式为：

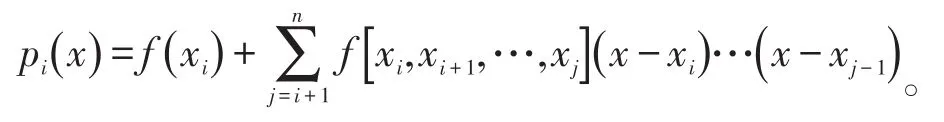
由式（2）可知，背景值

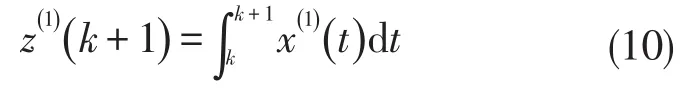
下面利用文献[17]中的有理插值方法，来构造背景值。

Step 1：构造有理插值函数。

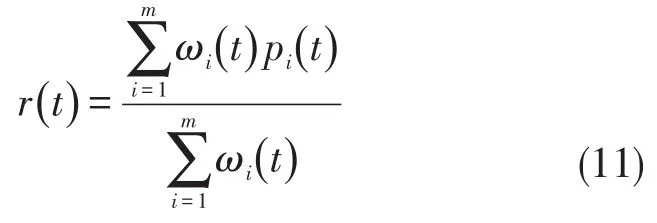
由式（6）和式（9）可得

Step 2：计算背景值

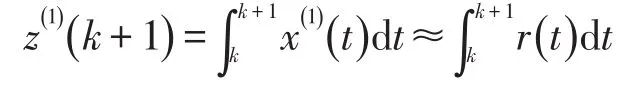
的数值积分。

将区间[k,k+1]划分为m等分，步长h=1/m，分点为tk,j=k+jh,j=0,1,…,m,根据文献[16]中的

复化梯形公式得：

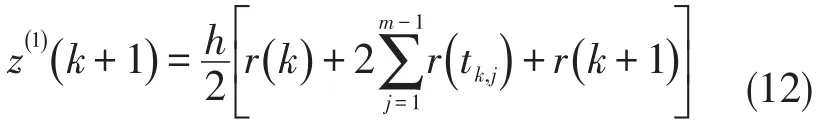
式（12）就是本文采用有理插值方法改进得到的GM(1,1)模型的新背景值，且非容易在各种软件上实现。将新背景值代入（5）式中，即可得到GM(1,1)的预测模型，且相比于其他方法具有如下优点：

（ⅰ）克服了原有构造方法的Runge现象发生而导致预测结果失真的情况。

（ⅱ）在滚动预测方面，也具有较低的计算复杂度。例如：原始数据的前k个原始时间序列，预测第k+1个数据x(0)(k+1)，然后添加第k+1个数据的预测值x^(0)(k+1)到原始序列的最后面，并删除原始序列的第一个数据x(0)(1)。这样就得到一个新的序列，去预测第k+2个数据x^(0)(k+2)。上述情况，使用其他方法构造背景值，每次都需要重新计算插值函数，而本文算法，只需要对pi(t)添加一项这样就节省了很多计算量。

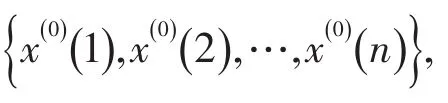
2 应用实例

2.1 数据描述

为了检验本文提出的预测模型精确性与适用性，采用2001-2013年我国国内生产总值总消费的数据为例进行预测研究，具体数据参见表1。主要考虑以下几方面的原因：（1）由于受国家经济水平的影响，我国的总消费总值持续增加，具有明显的指数分布特征，即选用其进行预测可以很好的反映所建立预测模型的真实水平；（2）国内生产总值总消费的预测容易受到多种不确定性因素的影响，如金融危机、自然灾害等均会在一定程度上影响预测的精确性，具有较明显的灰色预测模型的特征；（3）生产决定消费，国内生产总值决定了居民的消费水平，因此，对国内生产总值总消费进行科学预测，分析其发展趋势，为宏观经济政策的制定提供重要的参考，具有非常重要的意义。

2.2 方案设计

由于文献[13,14]已将其方法与其他文献进行了比较，验证其方法具有较高的预测精度和适用性。为了进一步体现本文方法的预测及模拟的效果，将本文与文献[13,14]的灰色预测模型模拟及预测结果进行比较分析，计算结果如下表2、3。其中本文所提出的有理插值模型（记为方法3）、组合插值模型[13]（记为方法1），三次样条插值模型[14]（记为方法2）。从表2、3可知，利用本文所提出的有理插值优化背景值的方法进行模拟和预测，和文献[14]相比几乎具有相同的预测精度，相比文献[13]具有较高的预测精度。进一步验证了背景值的重构是影响预测精度和适用性的关键因素，同时也表明了本文方法的有效性。

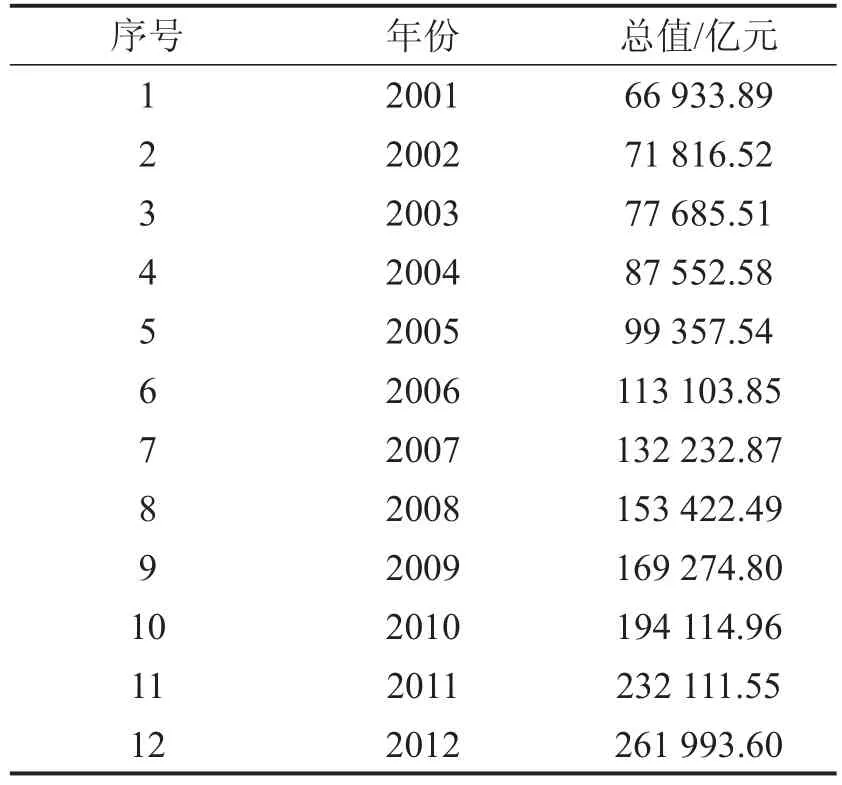
表1 2001-2013年中国国内最终消费的数据

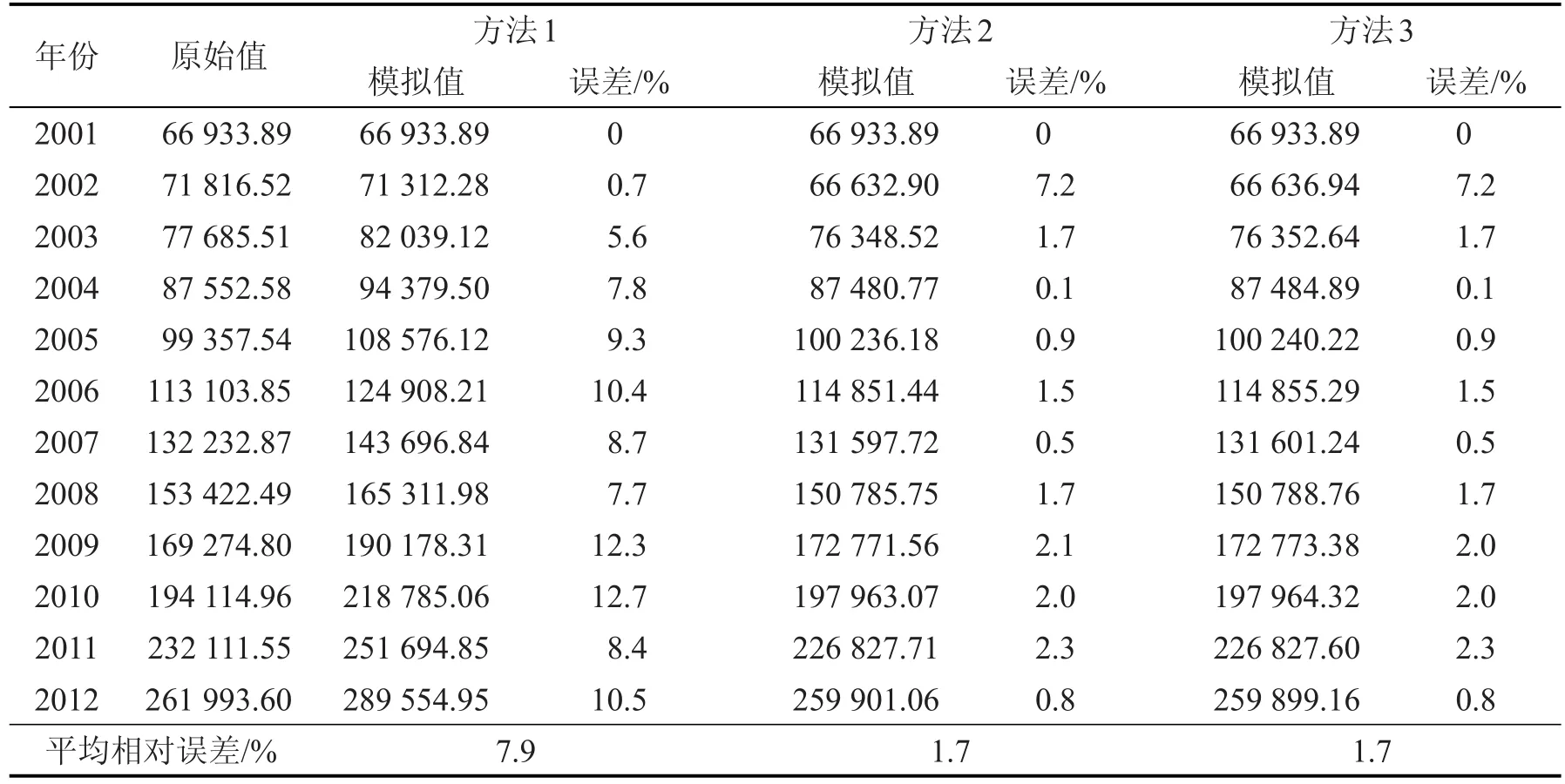
表2 2001-2012年国内总消费的模拟表

表3 2013年国内总消费的预测表

3 结束语

本文基于一种新的有理插值函数，给出GM(1,1)模型背景值构造的新方法，在减小计算量的同时提升了模型的预测性能，其主要优点包括：第一，计算量较低，特别是采用滚动和反馈校正的策略方面；第二，算法的可行性是无条件的；第三，具有较高的拟合和预测精度。实验研究表明，该方法充分改善了模型的稳定性与适用性，有效提高了模型的预测精度。

[1]Li G D,Masuda S,Nagai M.Predicting the subscribers of fixed-line and cellular phone in Japan by a novel prediction model[J].Technological Forecasting and Social Change,2014,81:321-330.

[2]Xia M,Wong W K.A seasonal discrete grey forecasting model for fashion retailing[J].Knowledge-Based Systems,2014,57:119-126.

[3]谭冠军.GM(1,1)模型的背景值构造方法和应用(Ⅲ)[J].系统工程理论与实践，2000，20（6）：70-74.

[4]刘思峰，邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践，2000，20（5）：121-124.

[5]Chao Z,Wang J,Chao J,et al.Using a grey model optimized by differential evolution algorithm to forecast the per capita annual net income of rural households in China[J].Omega,2012,40(5):525-532.

[6]Wang Y H,Dang Y G,Li Y E,et al.An approach to increase prediction precision of GM(1,1)model based on optimization of the initial condition[J].Expert Systems WithApplications,2010,37(8):5640-5644.

[7]罗 党，刘思峰，党耀国.灰色模型GM(1,1)的优化[J].中国工程科学，2003，5（8）：50-53.

[8]唐万梅，向长合.基于二次插值的GM(1,1)模型预测方法的改进[J].中国管理科学，2006，14（6）：109-112.

[9]李俊峰，戴文战.基于插值和Newton-Cores公式的GM(1,1)模型的背景值构造新方法与应用[J].系统工程理论与实践，2005，24（10）：122-126.

[10]唐利民.GM(1,1)病态问题求解的调整计量单位法[J].武汉大学学报:信息科学版，2014，39（9）：1038-1042.

[11]Wu L F,Liu S F,Yao L G,et al.Grey system model with the fractional order accumulation[J].Communications in Nonlinear Science and Numerical Simulation,2013,18(7):1775-1785.

[12]Wu L F,Liu S F,Fang Z G,et al.Properties of the GM(1,1)with fractional order accumulation[J].Applied Mathematics and Computation,2015,252:287-293.

[13]王晓佳，杨善林.基于组合插值的GM(1,1)模型预测方法的改进与应用[J].中国管理科学，2012，20（2）：129-134.

[14]Wang X J,Yang S L,Ding J,et al.Dynamic GM(1,1)model based on cubic spline for electricity consumption prediction in smart grid[J].China Communications,2010,7(4):83-88.

[15]吴宗敏，苏仰峰.数值逼近[M].北京：科学出版社，2008:42-73.

[16]王仁宏.数值逼近[M].北京：高等教育出版社，2012：173-218.

[17]Sidi A.Algebraic properties of some new vector-valued rational interpolants[J].Journal of Approximation Theory,2006,141(2):142-161.

Reconstruction of background value of GM(1,1)model based on rational interpolation function

KANG Ning,ZHANG Jing-jing,LI Xiao-ying
(School of Economic,Fuyang Normal University,Fuyang Anhui236037,China)

Based on rational interpolation function,a new class of Grey prediction model were put forward.This model improves the constructing approach of background value in the original model,which overcomes the deficiency of the existing GM(1,1)model,and provides a new way for improving the prediction accuracy.Compared with other approach,it not only has high prediction accuracy,but also has small computation.Finally,the example of total consumption data in China is presented to demonstrate the effectiveness of our approach.

rational interpolation;background value;GM(1,1)model;prediction accuracy

N941.5文献识别码：A

1004-4329（2017）04-068-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）04-068-05

2017-10-18

阜阳师范学院自然科学研究项目（2017FSKJ02ZD，2016FSKJ02）；阜阳师范学院青年人才基金重点项目（rcxm201711）资助。

康 宁（1986－ ），女，博士，讲师，研究方向：灰色系统理论、金融计量。