基于扰动的社交网络保护方法

范国婷，杨 颖，孙 刚，赵 佳

（阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037）

基于扰动的社交网络保护方法

范国婷，杨 颖，孙 刚，赵 佳

（阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037）

扰动技术是社交网络隐私保护的重要方法，本文提出了高斯随机扰动和贪心扰动两种扰动算法保护社交网络的权值，分别适用于动态和静态社交网络。高斯随机扰动可以简单有效地保护动态社交网络的权值隐私，贪心扰动算法将社交网络的边分类，可以在保护静态社交网络权值隐私的同时保证社交网络的最小生成树不变，提高社交网络数据的可用性。实验结果表明两种算法均能有效保护社交网络的权值安全，并且保持较高的数据可用性。

社交网络；隐私保护；扰动；权值

快速发展的社交网络存储了用户的大量个人信息，这些海量信息蕴含了丰富的价值，对社交网络数据进行数据挖掘能得到宝贵的知识，但是社交网络数据包含了用户的大量敏感信息，对社交网络数据挖掘前需要对其进行隐私保护处理。近年来，在保持社交网络数据可用性的同时，如何保护用户隐私成为一个严峻的问题[1]。目前社交网络的隐私保护研究主要集中在节点保护[2]和边保护[3-5]，保护社交网络中的用户身份和用户间的敏感关系不被发现。而权值是社交网络的一种重要特性，权值保护具有重要意义[6]。

权值需要保护主要有两方面原因，一是权值本身是敏感信息[7]，例如在一个商业交易社交网络中，节点代表不同的交易者，两个节点之间边的权值是交易者之间的交易金额，交易金额是隐私信息，需要对该信息进行保护[8]。另一种原因是权值可以作为攻击者的背景知识，例如在社交网络中，节点的身份是敏感的，利用权值可以推断社交网络的节点身份，此时也需要对权值进行保护。最小生成树是图论中的经典问题，具有重要应用价值，保护社交网络权值隐私的同时保证社交网络的最小生成树不变可以有效提高社交网络的数据可用性。

目前社交网络的权值保护研究主要有两种方向，一是通过改变权值，保护节点或边的身份，Skarkala等人[9]利用结点k-匿名机制，保护边的权重的同时将用户身份泄露概率降至1/k以内。文献[10]基于k-匿名思想，提出了一种k-权值模型，该模型确保匿名图中任意节点至少存在k-1个节点与其权值属性相同，从而保护节点身份文献。文献[11]在文献[10]的基础上提出了一种泛化模型，进一步保留了社交网络的一些基于权值的统计信息。另一种是不考虑节点和边的身份保护，保护权值的同时尽量保持社交网络的某些线性属性不变，从而提高社交网络的数据可用性。如Das等人在文献[12]中提出一种线性规划模型，使用不等式组约束权值，对边的权值提供隐私保护的同时保持图的最短路径等线性属性。Liu等人在文献[13]提出权值保护方案，同时保护节点间的最短路径尽量不变。为解决现有社交网络权值保护的不足，本文提出了两种社交网络权值保护方案，一种可以保护动态社交网络的权值，另一种可以在保护静态社交网络权值安全的同时，保持其最小生成树不变。

1 预备知识

本文将社交网络形式化定义为：G={V,E,W},节点集V={v1,v2,…,vn}代表社交网络的实体，vi可以代表个体、机构等，边集E={(vi,vj)|1≤i,j≤n,i≠j}代表社交网络实体间的社交连接关系，ei,j代表连接节点vi和vj之间的边，权值集W={(wij)|1≤i,j≤n,i≠j}代表社交网络的权值集合，权值wij代表边ei,j的权值，用变量n和m表示节点和边的数量。图1(a)显示了一个有权社交网络的抽象结构模型图。

本文用T表示社交网络的最小生成树（Minimum Spanning Tree，MST）边集，公式wT=∑wij(eij∈T)来计算社交网络的最小生成树的权值和，图1(a)所示的社交网络MST边集T={e1,2,e1,3,e1,6,e4,6,e5,6}，最小生成树的权值和wT=88。扰动后的社交网络表示为G*={V*,E*,W*}，w*ij表示扰动后节点vi和vj间的边权值，T*表示扰动后的社交网络最小生成树边集表示扰动后的社交网络最小生成树的权值和。

图1 社交网络模型

2 权值保护策略

本文介绍两种权值保护算法：高斯随机扰动算法和贪心扰动算法，高斯随机扰动可以简单有效地保护权值信息不被泄露。贪心扰动算法适应于静态社交网络，可以保证贪心扰动后的社交网络最小生成树结构和权值和不发生改变。

2.1 高斯随机扰动策略

W是社交网络G的权值集合，当两个节点间有边连接，wij的值是边ei,j的权值，当两个节点间没有边连接，则值为0，表示扰动后边的权值，N(0,δ2)代表一个n*n的对称高斯随机噪声矩阵，该高斯矩阵均值为0，标准偏差为δ，高斯随机扰动算法对每条边的权值扰动策略为：

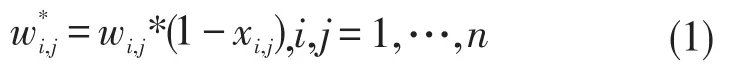
其中xi,j是满足高斯随机分布函数N(0,δ2)的随机数，图1(a)所示的社交网络使用高斯随机矩阵N(0,0.152)(δ=0.15)进行权值扰动后，得到的社交网络如图1(b)所示。

相比原社交网络G，高斯扰动后的社交网络G*结构未发生改变，即V=V*，E=E*，改变的仅仅是权值。高斯随机扰动策略中，扰动后的社交网络边的权值之和能保持在一定范围内，那么社交网络的很多线性属性（如最短路径长度等）接近原始值，保证了数据可用性。本节利用最小生成树的权值和证明，证明过程如下：

定理1高斯随机扰动策略中，

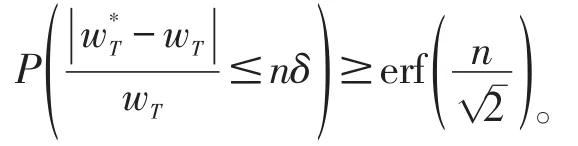
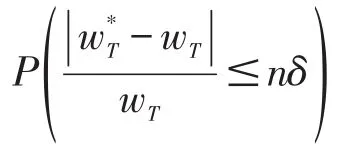
将上式左右分别相加可得

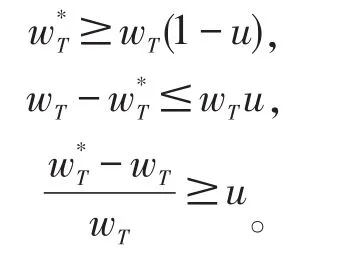
利用上述不等式的概率函数，可得

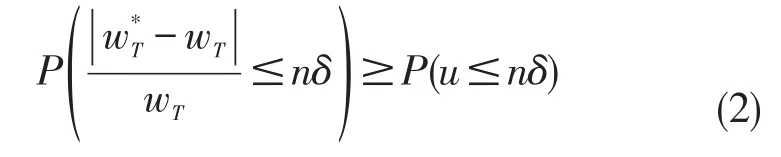
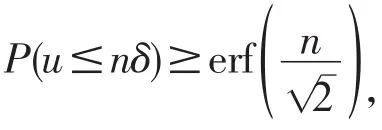
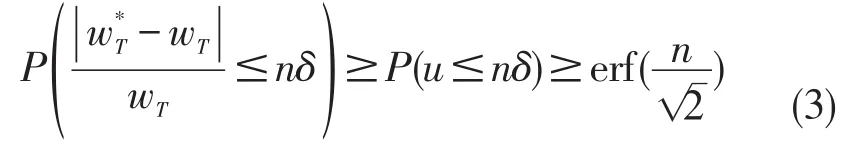
从前文可知，高斯随机扰动算法复杂度低，适用于动态社交网络权值保护，但是高斯随机扰动后的社交网络，很多基于权值的应用不能完全保持，如最小生成树的结构发生了改变，最小生成树的权值和也由88变为92。最小生成树作为社交网络中一种常见应用，其变化会影响社交网络的数据可用性，本文为保护扰动后的社交网络最小生成树不变，进一步提出了贪心扰动算法。

2.2 贪心扰动策略

贪心扰动算法的实现目标是生成社交网络G*={V*,E*,W*}，并且满足以下条件：

（ⅰ）T*=T，即扰动后的最小生成树包含的边集不变；

考虑到保护社交网络的最小生成树不变，并不是所有节点间的权值都不能改变，设计贪心扰动算法时，对社交网络的边进行分类处理，将原社交网络G中的边集E分为两类：不属于最小生成树的边和属于最小生成树的边。

定义1若边ei,j不属于最小生成树边集T，边ei,j定义为非归属边（ei,j∉T）。

原始社交网络的最小生成树边集T={e1,2,e1,3,e1,6,e4,6,e5,6}，则边e2,4,e3,5,e4,5是非归属边。对于非归属边ei,j，将其权值任意加上一个随机正值r，即实现那么最小生成树的结构不会发生变化，并且最小生成树的权值和也不受影响，即图2(a)显示了一种社交网络非归属边进行贪心扰动的过程，可见对社交网络的非归属边进行扰动不会影响最小生成树。

图2 贪心扰动策略

定义2若边ei,j属于最小生成树边集T，边ei,j定义为归属边（ei,j∈T）。

图1(a)所示的原社交网络最小生成树边集T={e1,2,e1,3,e1,6,e4,6,e5,6}，则边e1,2,e1,3,e1,6,e4,5,e4,6均为归属边，对于社交网络的归属边，有两种改变策略。

（ⅰ）增大策略

对于归属边ei,j，可以将它的权值加上一个随机值，新的权值，r需要满足其中是社交网络G-的最小生成树的权值，G-表示社交网络G删除边ei,j和权值wi,j后的社交网络G-={V,{E-ei,j},{W-wi,j}}，由于所以对某一归属边ei,j采取增大策略后，MST边集不会发生变化，而权值和会增大，即如图 2(b)，归属边e1,3=10，wT=88，，则r可取值5，那么对归属边采用增大策略进行扰动后的社交网络G*中，

（ⅱ）减小策略

图3显示了贪心扰动前后的社交网络，由图可见，经过上述贪心扰动后生成的社交网络G*，其最小生成树结构不会发生变化，即T*=T，最小生成树的权值也未发生变化，即

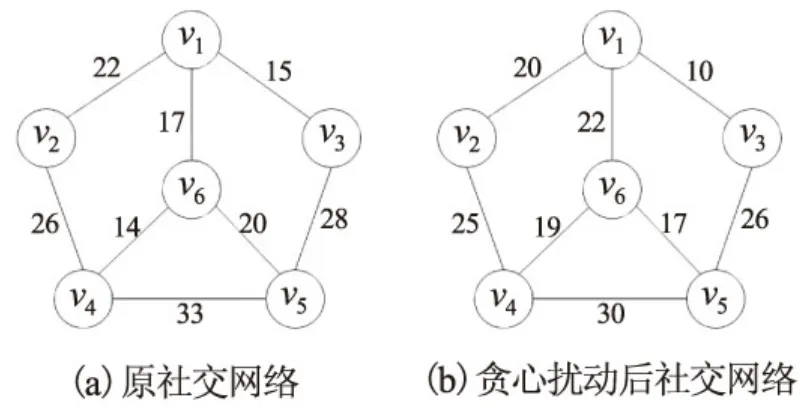
图3 贪心扰动后社交网络

2.3 算法分析

本文针对权值保护提出了两种扰动算法：高斯随机扰动和贪心扰动。高斯随机扰动的过程是将每条边的权值乘上一个高斯随机数，如果社交网络是动态的，那么对于后续新添进的边也做如此操作，由于本文假设社交网络中边的数量是m，所以高斯随机扰动的时间复杂度是O(m)。对于贪心扰动算法，需要对社交网络中的每一条边采取增大边权值或者减小边权值策略进行扰动，所以贪心扰动的时间复杂度也是O(m)，两种算法的时间复杂度相同。

3 实验与分析

3.1 实验数据集

实验所用数据集是数据集EIES Acquaintanceship at time 2，该数据集常用于有权社交网络分析，由Freeman等[15]收集，包含早期参加电子信息交换影响研究的若干研究者以及他们之间电子邮件的联系。数据集边上的权值代表他们之间的关系亲密度，由于该数据集是有向社交网络，本文在实验前将该社交网络变换为无向社交网络，生成实验需要的数据集。

3.2 实验结果分析

社交网络的权值保护研究中，文献[12]提出了一种线性规划模型（linear programming，LP），该模型能有效保护社交网络的权值，并且保证变化后的社交网络最小生成树尽量不变，本文实验部分将高斯随机扰动算法、贪心扰动算法与LP算法相比较，验证本文高斯扰动和贪心扰动算法的性能。试验从隐私保护性能、数据可用性和算法复杂度三方面比较。

3.2.1 隐私保护性能分析

高斯随机扰动、贪心扰动和LP算法均采用随机值对社交网络权值进行保护，高斯扰动算法中，权值乘上一个高斯随机数，改变后的权值相比较原始权值的变化范围在[-δ,δ]、[-2δ,2δ]、[-3δ,3δ]的概率分别近似于0.68、0.95、0.997。贪心扰动算法通过加减一个大于0的随机值改变权值，随机值r的取值取决于原社交网络的权值，真实权值被预测的概率根据随机值的大小变化而变化。LP算法中，通过一系列不等式组来约束随机值的大小，真实权值被预测的概率取决于不等式的约束条件。这三种算法处理后的社交网络，真实权值被预测的概率不定，取决于所选随机值的大小，高斯随机算法处理后的权值在一定范围变化，在隐私保护强度上略低于贪心扰动算法和LP算法。这三种算法处理后的社交网络真实权值被保护，具体的保护强度根据随机值不同而改变。

3.2.2 数据可用性分析

本文对社交网络的权值进行保护时，未改变社交网络的结构，所以试验选择最小生成树的权值和来衡量社交网络变化后的数据可用性。

图4显示了经过贪心扰动算法、高斯随机扰动算法和LP算法保护后的社交网络MST权值和与原始社交网络MST权值和的比较，由图4可以看出，贪心扰动后的社交网络MST权值和始终与原始社交网络保持一致，而高斯随机扰动算法和LP算法会造成最小生成树权值和的变化。高斯随机扰动最终的权值和与原始社交网络的权值和变化控制在一定范围内，MST结构可能变化。贪心扰动算法的目标是保证MST的结构与权值和不变。LP算法利用一系列不等式组对权值变化进行约束，保证生成的社交网络最小生成树结构不变，但是权值和有可能变化。因此，贪心扰动算法和LP算法均能保证变化后的社交网络MST的结构不发生改变，而高斯扰动算法处理后的社交网络最小生成树有可能发生变化，在数据可用性方面，贪心算法的性能最优。

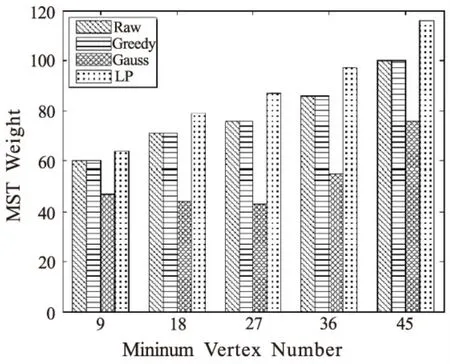
图4 最小生成树权值和比较

3.2.3 算法复杂度分析

图5显示了3种算法在处理数据集时所耗费的时间，从实验结果来看，高斯随机扰动耗时最短，贪心扰动耗时次之，LP算法耗时最长。从上文的算法时间复杂度分析可知，高斯随机扰动和贪心扰动的时间复杂度是O(m)，而文献[12]中的LP算法的时间复杂度是O(dm)，其中d是m条边的平均度。可以预见，随着数据集的不断增大，LP算法耗时相比本文算法耗时的差距会越来越大，所以本文所提算法在时间复杂度方面也表现出了优越性，而且在算法效率上，高斯随机扰动算法比贪心扰动算法更优。

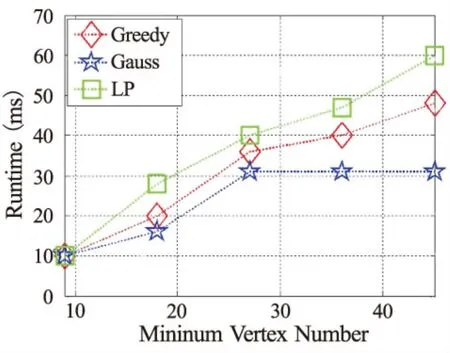
图5 算法运行时间

4 结束语

本文介绍了两种权值保护算法，高斯随机扰动算法实现简单，能够有效保护动态社交网络的权值，但是经过高斯随机扰动后的社交网络，很多基于权值的应用会发生变化，针对社交网络中的最小生成树应用，本文提出了贪心扰动算法，贪心扰动能保护静态社交网络的权值不被泄露，同时保证扰动后的社交网络最小生成树不变，保证社交网络的数据可用性。但贪心扰动策略需要提前获得社交网络的全部权值信息，无法有效应用于动态社交网络权值保护。在保持社交网络高数据可用性的同时，如何有效保护动态社交网络权值仍待进一步研究。

[1]Liu P,Li X.An improved privacy preserving algorithm for publishing social network data[C]//IEEE International Conference on High Performance Computing and Communications,2013:888-895.

[2]刘向宇，王 斌，杨晓春.社会网络数据发布隐私保护技术综述[J].软件学报，2014，25（3）：576-590．

[3]Fogues R,Such J M,Espinosa A A.Open challenges in Relationship-Based privacy mechanisms for social network services[J].International Journal of Human-Computer Interaction,2015,31(5):350-370.

[4]Zheleva E,Getoor L.Preserving the privacy of sensitive relationships in graph data[C]//Proceedings of the 1st ACM SIGKDD Workshop on Privacy,2007:153-171.

[5]Bazarova N N,Choi Y H.Self‐disclosure in social media:Extending the functional approach to disclosure motivations and characteristics on social network sites[J].Journal of Communication,2014,64(4):635-657.

[6]Liu C G,Liu I H,Yao W S,et al.K-anonymity against neighborhood attacks in weighted social networks[J].Security and Communication Networks,2015,8(18):3864-3882.

[7]谷勇浩，林九川，郭 达.基于聚类的动态社交网络隐私保护方法[J].通信学报，2015，36（Z1）：126-130．

[8]Wang S L,Tsai Y C,Kao H Y,et al.SHORTEST PATHS ANONYMIZATION ON WEIGHTED GRAPHS[J].International Journal of Software Engineering and Knowledge Engineering,2013,23(1):65-79.

[9]Skarkala M E,Maragoudakis M,Gritzalis S，et al.Privacy preservation by k-anonymization of weighted social networks[C]//IEEE/ACM international conference on advances in social networks analysis and mining,2012:423-428.

[10]Li Y,Shen H.Anonymizing graphs against weightbased attacks[C]Data Mining Workshops(ICDMW),2010 IEEE International Conference on.IEEE,2010:491-498.

[11]Liu X,Yang X.Ageneralization based approach for anonymizing weighted social network graphs[M]Web-Age Information Management.Springer Berlin Heidelberg,2011:118-130.

[12]Das S,Eğecioğlu O,El A A.Anonymizing weighted social network graphs[C]//IEEE 26th International Conference on,2010:904-907.

[13]Liu L,Wang J,Liu J,et al.Privacy preserving in social networks against sensitive edge disclosure，University of Kentucky,KY[R],2008.

[14]Stigler S M.Statistics on the table:The history of statistical concepts and methods[M].Harvard University Press,2002.

[15]Freeman L C,Freeman S C.A semi-visible college:structural effects on a social networks group.Electronic Communication:Technology and Impacts Boulder,Westview Press,1980:77-85.

Perturbation-based privacy preserving method in social networks

FAN Guo-ting,YANG Ying,SUN Gang,ZHAO Jia
(School of Computer and Information Engineering,Fuyang Normal University,Fuyang Anhui236041,China)

Perturbation methods are crucial privacy-protecting approaches for social networks.The Gaussian perturbing randomly algorithm and greedy perturbation algorithm were put forward for the weights protection of the social networks.Gaussian perturbing randomly algorithm was simple to protect the weights of dynamic social networks.The edges were classified in the greedy perturbation algorithm,so that make minimum spanning tree same,meanwhile which can protect the weight privacy in static social networks.Experiment results show that two algorithms can effectively protect the weight information in social networks.The Gaussian perturbing randomly algorithm is fit for dynamic social networks while greedy perturbation algorithm can better protect static social networks.

social network；privacy preserving；perturbation；weight

TP309文献识别码：A

1004-4329（2017）04-055-06

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）04-055-06

2017-07-25

安徽省高校省级重点科研项目（KJ2017A332，KJ2016A549）资助。

范国婷(1985－ )，女，硕士，助教，研究方向：信息安全域隐私保护。