基于服务合作的双渠道供应链定价策略研究
2018-01-04刘冀琼
冯 帅 ,刘冀琼
(1.阜阳师范学院 商学院,安徽 阜阳 236037;2.区域物流规划与现代物流工程安徽省重点实验室,安徽 阜阳 236037)
基于服务合作的双渠道供应链定价策略研究
冯 帅1,2,刘冀琼1,2
(1.阜阳师范学院 商学院,安徽 阜阳 236037;2.区域物流规划与现代物流工程安徽省重点实验室,安徽 阜阳 236037)
本文以制造商、网络零售商和传统零售商组成的分散结构双渠道为研究对象,考虑网络零售商以报酬的形式将其服务交由传统零售商完成的情形,构建了基于服务合作的双渠道供应链定价模型。通过博弈得出了网络零售商和传统零售商分别在制造商领先的Stackelberg博弈下以及集中决策下的最优定价,并分析了服务水平和服务成本系数对渠道价格和需求数量的影响,最后利用Matlab模拟其变化趋势以验证双渠道服务合作定价策略的结论。
双渠道供应链;服务合作;博弈;定价策略
电子商务和网络技术的快速发展使得网络零售的规模日益增长,越来越多的供应链采取在传统渠道的基础上开辟网络渠道,同时在两个渠道上进行产品销售。网络渠道的开辟所带来的好处以及由此引发的各种问题一度掀起了众学者研究的热潮。部分学者就网络零售渠道开辟后的双渠道价格、渠道冲突以及对传统零售渠道的影响乃至双渠道供应链协调等问题进行了研究。Jing等研究了双渠道供应链中的价格和质量决策,而且证明了当引入新的渠道时,可以实现质量改进[1]。Liu等从信息是否完全的角度分析了风险规避会对双渠道供应链的政策产生什么样的影响[2]。Li等的研究发现渠道效率随着消费者对零售渠道的忠诚度的增长而增加,随着零售商的公平性问题的增加而下降,并且得到了零售商提供增值服务并且有公平的顾虑时,整个供应链不能与恒定的批发价格协调的结论[3]。丁正平等通过建模分析了不同结构的双渠道供应链存在顾客搭便车行为时的定价策略和收益共享契约问题[4]。陈军等对比分析了零售商为双渠道提供差异化服务和无差异服务时对双渠道双方各自利润的影响,得出了差异化服务可以提高渠道利润的结论[5]。张国兴等对不同权力结构下的双渠道供应链展开博弈分析[6]。谭江涛等研究了通过合理的双渠道定价协调网络零售商和传统零售商的冲突问题[7]。李明结合物流成本,研究了电商如何进行合作可以实现帕累托最优,以及实现的条件[8]。祖峰等则从消费者对网络的接受程度的角度,对比研究了提供补偿激励与否对双渠道价格的影响,以及如果提供补偿激励的话双方的定价和补偿额度应该是多少的问题[9]。
综上所述,现有文献大多集中在渠道冲突、双渠道供应链契约定价与协调策略的研究上,关于考虑网络零售商和传统零售商通过服务合作的方式实现双渠道供应链合理定价的研究还很缺乏。事实上,不同渠道的零售商在服务层面达成合作,一方面网络零售商可以提高自身的服务水平,而另一方面传统零售商也可以收取相应的服务酬劳。显而易见,服务合作是一个双赢的局面。因此,本文针对制造商、传统零售商和网络零售商三个主体组成的分散双渠道结构,在传统零售商对双渠道提供差异化服务的前提下,研究网络零售商和传统零售商进行服务合作时供应链各方的最优定价策略,这也是本文的创新点所在。最后,通过数值算例验证本文所得双渠道价格和需求数量与服务水平以及服务成本系数的变化关系。
1 基于服务合作的双渠道供应链定价策略模型
1.1 问题描述
服务水平作为顾客是否购买产品的一个重要标准,对顾客购买决策的影响作用日趋明显。双渠道供应链系统中,网络零售渠道较传统零售渠道往往更具价格优势,而传统零售渠道凭借其更为接近顾客的特性较网络零售渠道更具服务优势。网络零售商考虑以支付服务费用的方式将其相关服务交由传统零售商完成,双方展开渠道间的服务合作,而这一问题的关键在于渠道双方零售商应如何合理定价以实现自身利益的最大化。
本文研究基于服务合作的分散双渠道结构的各供应链主体分别在分散和集中决策模式下的供应链定价策略。所谓分散双渠道结构是指网络渠道由专门从事网络销售、介于制造商和传统零售商之外的第三方开辟,此时供应链系统中包括制造商、传统零售商和网络零售商三个主体,如Amazon。制造商同时向传统零售商和网络零售商供应同质产品,网络零售商将其服务交由传统零售商完成,传统零售商从中收取相应的费用,服务合作结构模型如图1所示。
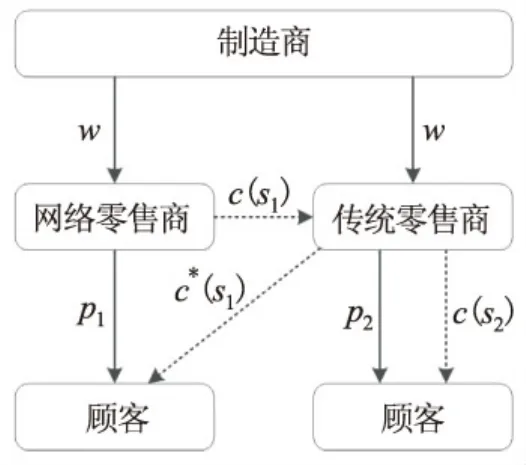
图1 双渠道服务合作结构模型
当双渠道供应链系统含有多个主体,其中制造商实力较强且分散决策时,基本的博弈顺序为:(1)作为Stackelberg博弈领导者的制造商首先以其自身利润最大化为目标制定批发价格;(2)不隶属于同一主体的双渠道零售商进行Bertrand博弈,分别决策出不同渠道上产品的零售价格。集中决策时,双渠道供应链各方被看作一个整体,其目的是追求整个双渠道供应链的总利润最大,以此为目标函数决策不同渠道上产品的零售价格。
1.2 模型分析
1.2.1 需求函数
两个零售渠道存在价格和服务双重竞争关系,在建立渠道需求函数时应不但要考虑自身价格和服务水平对需求的影响,同时还应考虑与竞争渠道的价格和服务水平差异对自身需求的影响。本文由Bertrand价格博弈模型的思想作为启发,建立如下双渠道需求函数:

其中di(i∈{1,2})表示产品在渠道i上的需求数量(i=1表示网络零售渠道,i=2表示传统零售渠道);ai表示渠道i的潜在市场规模;pi表示渠道i的产品单位零售价格;si示渠道i的服务水平;δ1和δ2分别表示市场需求对价格和服务的弹性系数;θ1和θ2分别表示市场需求对价格差异和服务差异的转移系数,并假设δ1>θ2,即各渠道自身价格和服务对市场需求影响大于其竞争渠道的影响。
1.2.2 利润函数
假设不同渠道零售商的服务成本c(s)是其服务水平s的二次函数[10-11]。不妨设这样的假设一方面使得问题可解,另一方面体现了服务成本随服务水平的提高而增加越快的特征,其中k为零售商的服务成本系数。因此,渠道i上零售商的服务成本可以表达为:

传统零售商较网络零售商更具接近顾客的服务优势,其服务成本系数往往比网络零售商更低,即k2<k1。当网络零售商将其服务水平为s1的相关服务交由传统零售商完成时,需按服务成本系数k1支付服务费用c(s1)d1,而传统零售商只需按其服务成本系数k2为网络零售商的终端顾客提供服务水平为s1的相应服务,因此,整个过程中传统零售商从网络零售商处赚取得的服务费用为
① 制造商的利润函数
制造商的利润主要通过向网络零售商和传统零售商销售产品获得,其利润函数为:

其中w为制造商给网络零售商和传统零售商的产品单位批发价,c为制造商的产品单位生产成本。
②网络零售商的利润函数
网络零售商的主要收入来自于网络渠道上的产品销售,同时其成本支出包含支付给制造商的产品进货费用和支付给传统零售商的服务费用两部分,因此网络零售商的利润函数可表达为:
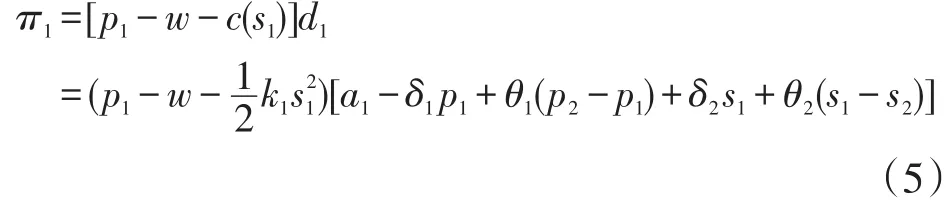
③传统零售商的利润函数
传统零售商在线下零售渠道销售产品获取收入,同时传统零售商还会从网络零售商处收取的服务费用,这两部分共同构成了网络零售商的总收入。费用支出方面,网络零售商一方面需支付给制造商进货费用,另一方面还需承担两类终端客户的服务成本,因此传统零售商的利润函数可表达为:
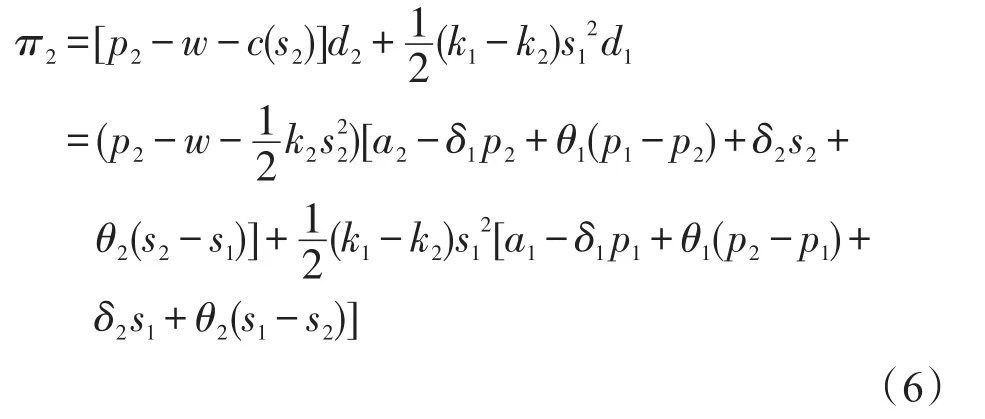
1.3 Stackelberg博弈模型定价决策及相关命题
分散决策时,博弈顺序为制造商首先决策产品的批发价格w,然后网络零售商和传统零售商再各自决策其零售价格p1和p2。根据逆向归纳法,π1和π2分别对p1和p2求导并令其为0,可得关于p1和p2的二元一次方程组:

求解该方程组可得:

将求得的p1和p2带入π0,同时对w求导并令其为0得到关于w的方程:

求解该方程可得

将(9)式带入(7)式和(8)式可得:

命题1在考虑服务合作、制造商作为Stackelberg博弈领导者的分散双渠道供应链系统中进行分散决策时,网络零售商和传统零售商的最优定价分别满足式(10)和式(11),制造商的最优批发价满足式(9)。
推论1在分散双渠道供应链系统中,网络零售商和传统零售商的零售价格与其各自的服务水平正相关。
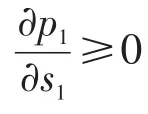
推论2网络渠道的服务水平对网络零售价格的影响大于对传统零售价格的影响;零售渠道的服务水平对传统零售价格的影响大于对网络零售价格的影响。
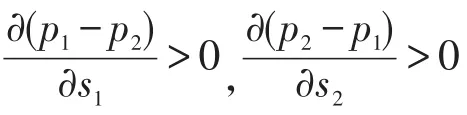
推论3网络渠道的零售价格与其服务成本系数正相关;传统渠道的零售价格与其服务成本系数正相关。

1.4 集中决策模式下模型定价决策及相关命题
集中决策时,制造商、网络零售商和传统零售商被看作一个整体,共同决策,追求的是整个双渠道供应链系统的总利润最大化。此时,供应链系统的总利润在给定参数下,是渠道零售价格p1和p2的二元函数,不妨记为π(p1,p2),则

在π(p1,p2)中分别对p1和p2求一阶偏导数,并令其等于零,得如下方程组

求解该方程组可得
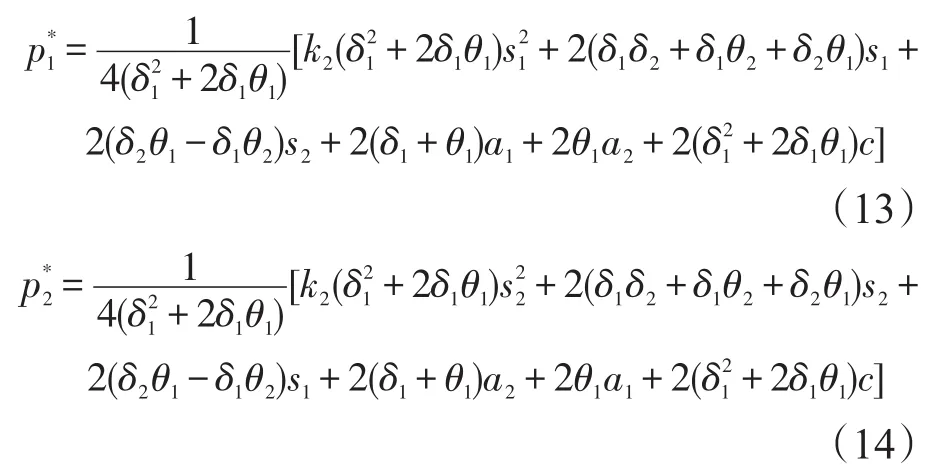
命题2在考虑服务合作的分散双渠道供应链系统中进行集中决策时,网络渠道和传统渠道的最优定价分别满足式(13)和式(14)。
推论4网络零售商和传统零售商的零售价格与其各自的服务水平均正相关。
证明因为所以推论4成立。
推论5网络渠道的服务水平对网络零售价格的影响大于对传统零售价格的影响;零售渠道的服务水平对传统零售价格的影响大于对网络零售价格的影响。
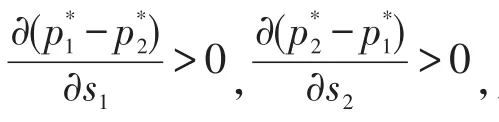
推论6集中决策模式下,双渠道的零售价格均与传统渠道的服务成本系数正相关,而与网络渠道的服务成本系数无关。
证明由式(13)和式(14),集中决策模式下双渠道的产品最优定价和显然和网络渠道服务成本系数k1无关。同时,故推论6成立。
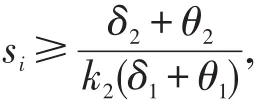
证明因为

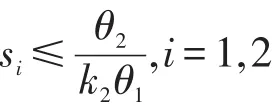

2 算例仿真与分析
2.1 渠道服务水平对价格的影响
基于以上分析,在分散的双渠道供应链系统中,对相关参数赋值如下:

(ⅰ)双渠道价格与网络渠道的服务水平s1
为分析网络渠道的服务水平s1单独变化时对双渠道价格的影响,传统渠道的服务水平s2应取某一定值,不妨设s2=5。

图2 双渠道价格与网络渠道的服务水平s1的变化关系
由图2可知,无论是在制造商占主导地位的Stacklberg博弈模型中,还是在集中决策模式下,网络渠道的零售价格随着其渠道服务水平的提升呈现出上升的趋势。这表明,网络渠道的服务水平s1越高时,网络渠道顾客所承担的支付价格也相应变得更高(推论1和推论4)。同时,无论在哪种决策模式下,传统渠道的零售价格几乎不受网络渠道服务水平的影响。这表明网络渠道的服务水平对其自身渠道的零售价格的影响大于对传统渠道零售价格的影响(推论2和推论5)。
(ⅱ)双渠道价格与传统渠道的服务水平s2
为分析传统渠道的服务水平s2单独变化时对双渠道价格的影响,网络渠道的服务水平s1应取某一定值,不妨设s1=5。
与图2类似,从图3中可以看出,在两种不同的决策模式下,传统渠道的零售价格随着其渠道服务水平的提升呈现出上升的趋势。这表明传统渠道的服务水平s2越高时,传统渠道顾客所承担的支付价格也相应变得更高(推论1和推论4)。同时,传统渠道服务水平对网络渠道零售价格的影响甚微。这表明传统渠道的服务水平对其自身渠道的零售价格的影响大于对网络渠道零售价格的影响(推论2和推论5)。
2.2 渠道服务成本系数对价格的影响
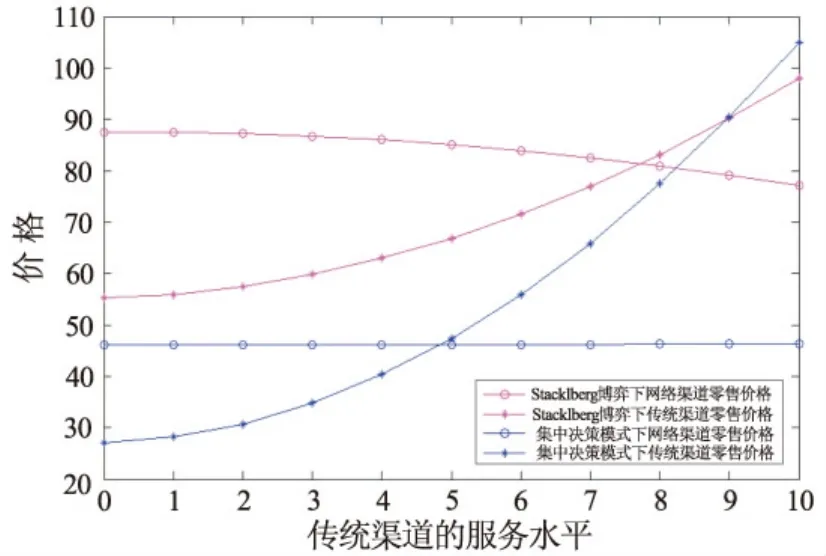
图3 双渠道价格与传统渠道的服务水平s2的变化关系
相关参数赋值如下:
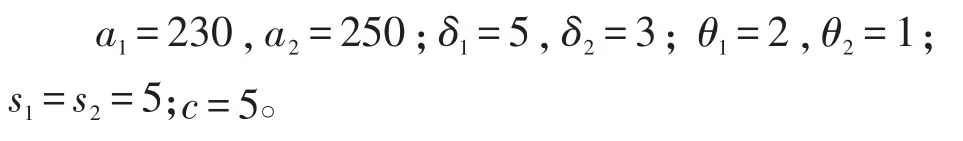
(ⅰ)双渠道价格与网络渠道的服务成本系数k1
为分析网络渠道的服务成本系数k1对双渠道价格的影响,设k2=3。
由图4可知,在Stacklberg博弈模型中,双渠道的零售价格与网络渠道的服务成本系数k1均呈现出正相关关系(推论3)。而在集中决策模式下,双渠道的零售价格与网络渠道服务成本系数k1无关(推论 6)。

图4 双渠道价格与网络渠道的服务成本系数k1的变化关系
(ⅱ)双渠道价格与传统渠道的服务成本系数k2
为分析传统渠道的服务成本系数k2对双渠道价格的影响,设k1=7。
由图5可以看出,在Stacklberg博弈模型中,传统渠道的零售价格随着其渠道的服务成本系数k2的增加而稍微上升(推论3),而网络渠道的零售价格对传统渠道的服务成本系数的变化却比较迟钝,几乎不受其影响。而在集中决策模式下,双渠道的零售价格均随着传统渠道服务成本系数k2的增加而显著提高(推论6)。

图5 双渠道价格与传统渠道的服务成本系数k2的变化关系
2.3 渠道服务水平对渠道需求数量的影响
对相关参数赋值如下:a1=230,a2=250;δ1=5,δ2=3;k1=7,k2=3;θ1=2,θ2=1;c=5。同时,为探讨单一渠道服务水平对双渠道需求数量的影响,先后令s2=5和s1=5。
由图6可知,集中决策模式下,双渠道的需求数量与自身渠道服务水平明显呈负相关关系,而与其竞争渠道的服务水平呈轻度正相关关系(推论7和推论8)。这主要是由于渠道价格与其渠道服务水平严格正相关(推论4),当期渠道服务水平越高时,其渠道零售价格相应也会越高,而需求与价格反向变化,因此需求会减少。同时,当某一渠道零售价格随着其服务水平升高时,就会导致越来越多的顾客转移至其竞争渠道,因此其竞争渠道的需求数量反而会增加,即渠道需求数量与其竞争渠道。
3 小结

图6 渠道需求数量与渠道服务水平的变化关系
网络渠道较传统渠道具有明显的价格优势,传统渠道凭借其更为接近顾客的特性较网络渠道更具服务优势,而事实上不同渠道的零售商可以在服务层面达成合作以实现利润的共同增长。本文基于分散双渠道结构的供应链,探讨供应链各主体考虑服务合作分别在分散和集中决策模式下的供应链定价策略问题,并通过数值算例分析了渠道零售价格与渠道服务水平、服务成本系数,以及渠道需求数量与渠道服务水平等经济变量之间的数量变化关系。研究表明,在不同渠道之间展开服务合作以实现利润的共同增长是可行且具实际意义的。
[1]Chen J X,Liang L,Yao D Q,et al.Price and quality decisions in dual-channel supply chains[J].European Journal of Operational Research,2017,259(3):935-948.
[2]Liu M Q,Cao E B,Salifou C K.Pricing strategies of a dual-channel supply chain with risk aversion[J].Transportation Research Part E-Logistics and Transportation Review,2016,90(SI):108-120.
[3]Li Q H,Li B.Dual-channel supply chain equilibrium problems regarding retail services and fairness concerns[J].Applied Mathematical Modelling,2016,40(15/16):7349-7367.
[4]丁正平,刘业政.存在搭便车时双渠道供应链的收益共享契约[J].系统工程学报,2013,28(3):370-376.
[5]陈 军,何 圆,赖 信.基于差异化服务的双渠道供应链服务合作策略[J].重庆交通大学学报(自然科学版),2015,34(2):118-123.
[6]张国兴,方 帅,汪应洛.不同权力结构下的双渠道供应链博弈分析[J].系统工程,2015,33(3):52-59.
[7]谭江涛,李棚成,何伟军,等.零售商双渠道供应链的定价与协调机制研究[J].数学的实践与认识,2016,46(17):121-128.
[8]李 明.电商环境下双渠道供应链的冲突协调研究[J].物流科技,2017,40(3):113-118.
[9]祖 峰,刘力钢,李 昕.关于双渠道供应链最优定价策略研究[J].价格理论与实践,2017(1):153-156.
[10]TsayA,Aggrawal N.Channel dynamics under price and service competition[J].Manufacturing&Service Operation Management,2000,2(4):372-391.
[11]许明辉,于 刚,张汉勤.具备提供服务的供应链博弈分析[J].管理科学学报,2006,9(2):18-27.
Research on the pricing strategy of dual-channel supply chain based on service cooperation
FENG Shuai1,2,LIU Ji-qiong1,2
(1.School of Business,Fuyang Normal University,Fuyang Anhui236037,China;2.Anhui Provincial Key Laboratory of Regional Logistics Planning and Modern Logistics Engineering,Fuyang Anhui236037,China)
The paper takes a decentralized dual-channel supply chain composed by a manufacture,online retailer and a traditional retailer as the object of study,and considers the condition that online retailer transfers the direct channel’s services to traditional retailer as reward.A dual-channel supply chain pricing model based on service cooperation is constructed.The optimal pricing of manufacture leader in the Stackelberg game and the centralized decision-making mode can be obtained by the game,and the influence of service level and service cost coefficient on channel price and demand quantity is analyzed.Finally,the changing trends of the prices and demand quantity under different levels of service is simulate by Matlab,and the conclusion of the pricing strategy is verified.
dual channel supply chain;service cooperation;game;pricing strategy
C931文献识别码:A
1004-4329(2017)04-061-07
10.14096/j.cnki.cn34-1069/n/1004-4329(2017)04-061-07
2017-09-22
安徽省自然科学研究项目(2014KJ007,KJ2017A335);安徽省教育厅重点项目(SK2016A0694)资助。
冯 帅(1983- ),男,博士生,讲师,研究方向:供应链管理、优化决策。
