一类具有时滞和非连续治愈的脉冲SEIR模型分析

费荔枝，吕恒民，季伟伟

（吉安职业技术学院 a.师范学院；b.公共基础课教学部，江西 吉安 343000）

一类具有时滞和非连续治愈的脉冲SEIR模型分析

费荔枝a，吕恒民b，季伟伟b

（吉安职业技术学院 a.师范学院；b.公共基础课教学部，江西 吉安 343000）

文章研究了具有时滞和非连续治愈的脉冲SEIR传染病模型，运用脉冲微分方程的比较定理，得到系统无病周期解的全局吸引性和全局渐进稳定性条件，通过计算得到了疾病消亡与否的阈值R*和R*当R*＜1时疾病会消亡；当R*＞1时疾病持久存在，最终会形成地方性疾病。

传染病；时滞；脉冲接种；持久性

传染病是有病毒、细菌等病原微生物和寄生虫感染人体后产生的具有传染性的疾病，给人类的生存带来了很多的危害，严重影响着人类的生活和社会经济[1]。传染病在其传播的过程中，其表现的形式是多样的，比如艾滋病，乙肝等在人类感染之后并不会马上有临床症状，而是在人体内潜伏若干年后有所表现，这样以来就出现时滞效应。近年来，具有时滞的传染病模型在不同程度上受到国内外学者共同关注[2-4]。而对传染病的预防和控制，学者们研究了连续接种[5]和脉冲接种[6],像麻疹、乙肝、结核等传染病来说，采用脉冲接种是一种非常有效的控制疾病的策略[7]；像疟疾、班氏丝虫病、马来丝虫病、乙型脑炎、登革热等依靠媒介传播的疾病，脉冲扑杀媒介也是控制疾病传播有效策略[8]。为更真实的描述的传播过程及预防和控制，人们往往同时将时滞和脉冲接种考虑在模型之中,这就构成了时滞脉冲传染病模型，其分析方法有别于时滞微分方程和脉冲微分方程。基于以上论述我们将建立具有疾病潜伏期、脉冲预防接种和分时断治疗的SEIR模型分析，将利用脉冲比较方程理论和右端不连续微分方程理论讨论系统无病周期解和地方病周期的相关性态。

1 SEIR传染病模型的建立

Zhang等在文献中研究了带有双线性的SEIR传染病模型[9]：

其中，S(t)表示易感者，E(t)表示感染疾病没有爆发的潜伏者，I(t)表示感染者，R(t)表示恢复者。在系统（1）中，作者仅考虑非连续治愈h(I)，而现实环境中许多传染病具有一定的潜伏周期，时滞的出现很好的的解释了这一现象。同时，在控制传染病的策略中脉冲接种是人常用的一种方法。因此，我们将研究如下带有脉冲接种策略和时滞的传染病模型：

其中，Λ为易感类出生率，μ为自然死亡率，γ为恢复率，τ表示传染病的潜伏周期。函数h(I)=φ(I)I表示治愈率，且0≤h(I)≤1。其中，φ(I)随感染类I(t)的增加而增加。为便于研究，假设：

(H1)φ:是单调不减且是分段连续的,即除了可数个孤立的点是间断的，其他点都是连续的。不失一般性，φ在I=0时是连续的，否则,我们可以修改φ在0的取值为φ(0+)，可以发现这样做并不会改变h在0的取值，即我们仍有h(0)=0，并且不会引起系统(2)和(3)的变化。定义φ(0)是φ(.)的极限，即φ(0-),φ(0+)分别是φ(I)的左极限和右极限，当I→0-或I→0+。

因为系统（2）的第一和第三个方程中没有E(t)和R(t)，所以系统（2）可简化为：

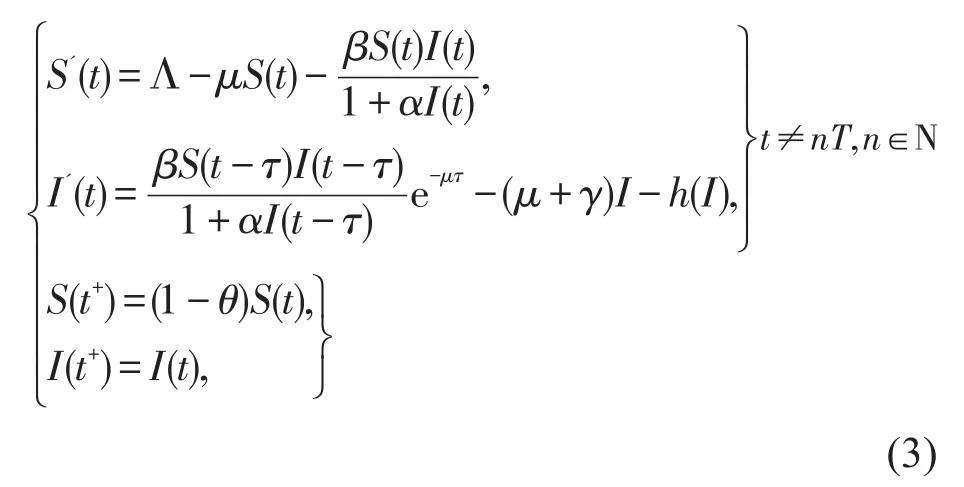
系统（3）的初始条件为：S(θ)=ϕ1(θ),I(θ)=ϕ2(θ),其中，是分段函数在第一类不连续点-nT(n∈N)的左连续，即ϕ(-nT-)=ϕ(-nT)上的空间，其中同时C又是Banach空间，且有唯一的模：

设N(t)=S(t)+E(t)+I(t)+R(t)，由系统（2）前四个方程相加可得：

因此个体总量在某一时间内是可变的，并且N(t)在t∈[0,+∞)是连续的。由系统（4）可得因为和I′(t)|s=0=0，在t≠nT,n∈N时，有S(nT+)=(1-θ)S(nT),1(nT+)=1(nT),n∈N。

如果系统（3）在[0,T)的任何紧子空间内是连续的，并且在[0,T)的每一处都满足如下微包方程

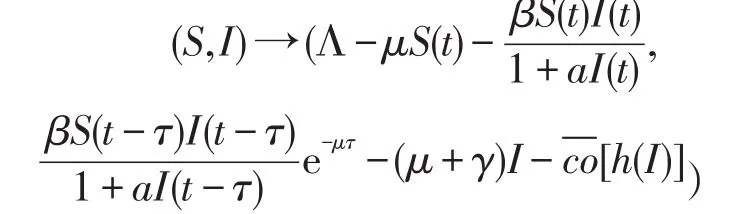
且该映射是一非空紧凸值的上半连续集值映射。

注意到(H1)意味着并且h(I)在0连续。根据φ在I=0的连续性，存在正常数ℓ使得当时,φ(I)是连续的并且(5)中的微分包含式变成下面的右端连续的微分方程:

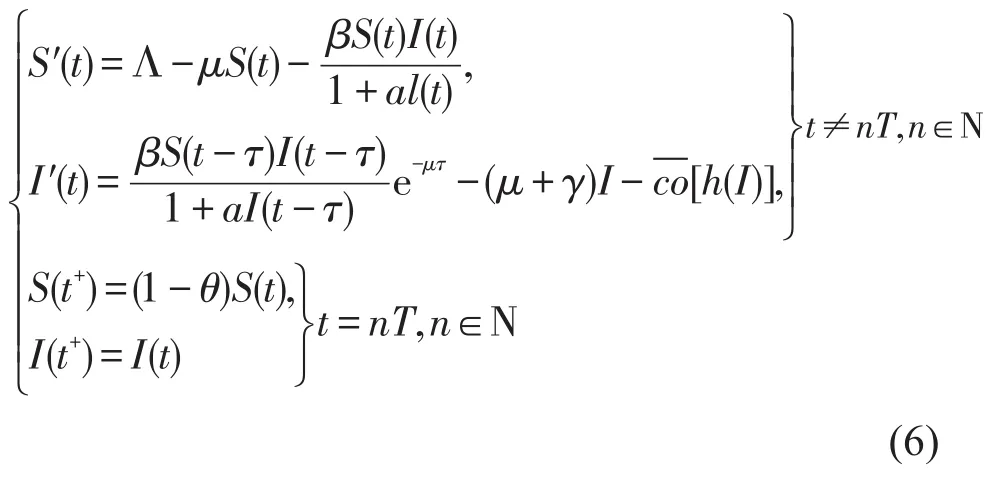
由上面的讨论，可得一下引理：

引理 1Ω是系统（6）的正不变集，其中充分小。

引理2[10]下列脉冲微分方程

如果a＞0,b＞0,0＜θ＜1，则系统（7）存在唯一全局渐进稳定的正周期解

引理3[11,12]下列时滞微分方程

其中，a1,a2和τ正常数，且x(t)＞0,当t∈[-τ,0]时，则有：

(i)如果a1＜a2则

(ii)如果a1＞a2则

2 模型的吸引性

首先，当所有t≥0时I=0，分析无病周期解的存在性。易感类S(t)在t∈(nT,(n+1)T]时满足如下方程组：

由引理2，可以得到系统（7）的全局渐进稳定的周期解：

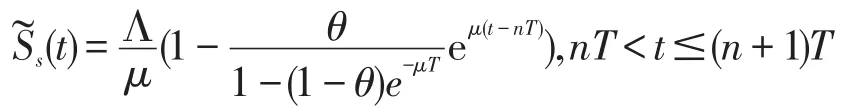
定理1如果R*＜1,则无病周期解(s(t),0)在Ω上是全局吸引的，其中

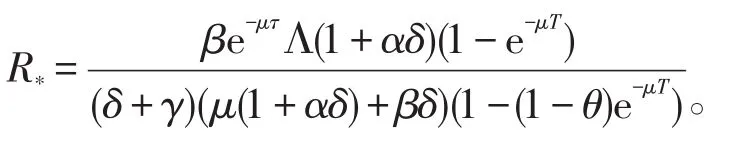
证明因为R*＜1，取充分小的ϵ0＞0使得βe-μτξ＜δ+γ。

由系统（6）的第一个方程得

由引理2得系统（8）有唯一全局渐进周期解

设 (S(t),I(t))是系统（6）的解 ，S(θ)=ϕ1(θ),θ∈[-τ,0],u(t)是系统（8）在初值条件u(θ)=ϕ1(θ),θ∈[-τ,0]下的解。由脉冲比较方程定理可得,存在一个常数n1使得

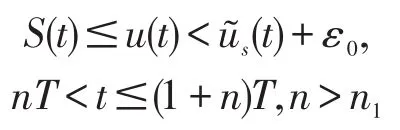
进一步可得

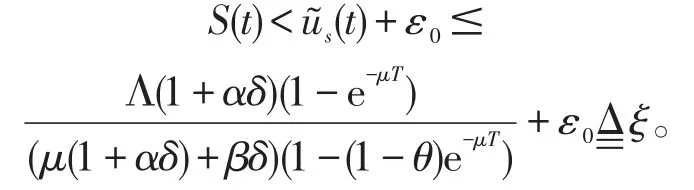
由系统（6）的第二个方程得

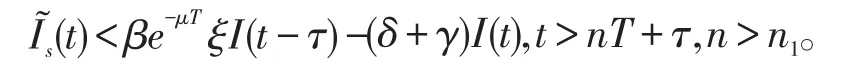
考虑如下辅助系统

由引理3可得

根据比较定理和I(t)的非负性可得

因此，对于充分小的ε0＞0,存在一个常数n2＞n1(其中n2T＞n1T+τ)使得，如果t＞n2T，则I(t)＜ε0。

从系统（6）的第一个方程，当t＞n2T+τ时，有S′(t)＞Λ-(μ+βε0)S(t)和根据比较定理和I(t)的非负性可得

我们考虑下面两个比较脉冲方程对于t＞n2T+τ和n2＞n1，

由引理 2可知，系统（11）和（12）有唯一全局渐进稳定的周期解分别是：

由脉冲比较方程可知，存在一个常数n3＞n2,使得n3＞n2+τ且

因为ε0可以任意小，所以由（13）可得

由（10）和（14）可知，系统（6）的无病周期解是全局吸引的。定理证毕。

由定理1，易得如下结论。

推论1如果则系统（6）的无病周期解是全局吸引。

推论2假设如 果θ＞θ*或T＜T*或τ＞τ*，则系统（6）的无病周期解(Ss(t),0)是全局吸引的，其中，

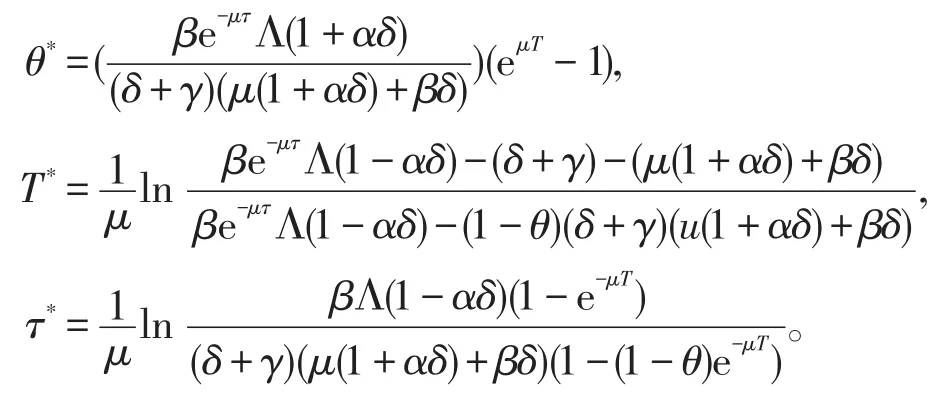
3 模型的持久性

在一个相当长的时间内，如果感染类持续在某一个阈值水平之上，称该传染病为地方病。在研究传染病的持久性之前，先给出有关定义和引理。

定义1如果存在常数η＞0（独立于初始条件）使解(S(t),I(t))在初始条件（3）不变的情况下满足

则称系统（6）是一致持久的。

记两个等式：

引理 4如果R*＞1，则对任意t0＞0，不可能有I(t)＜I*对所有的t≥t0。

证明假设矛盾，则有t0＞0使得I(t)＜I*，对所有t≥t0。根据系统（6）的任意解(S(t),I(t))，定义

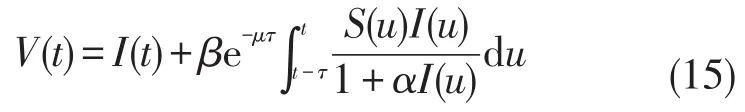
系统（6）的第二个方程可以写为

可以得到V沿着系统（6）解得导数

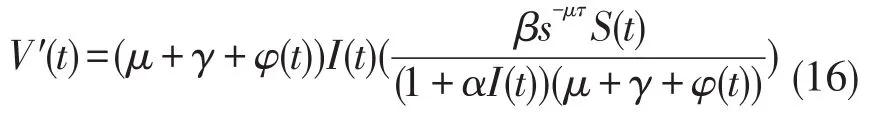
由系统（6）的第一个方程可得

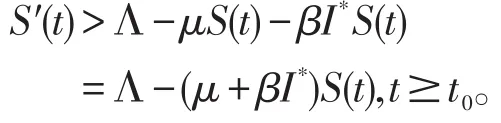
则可以构建比较方程，对t≥t0,

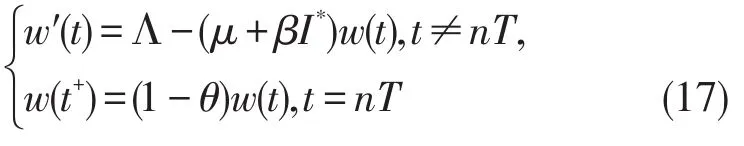
由引理2，可得系统（17）唯一的全局渐进稳定的周期解，对nT＜t≤(n+1)T,有

由脉冲比较方程定理可知，存在一个整数t1(t1＞t0)和充分小的ε＞0使得

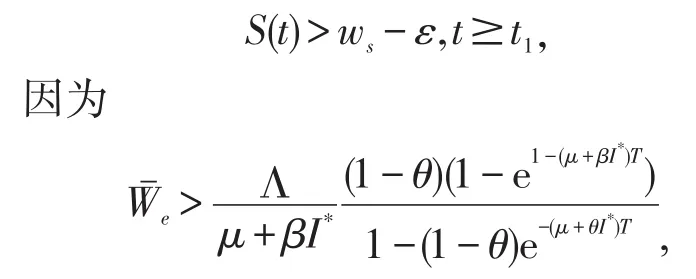
则有

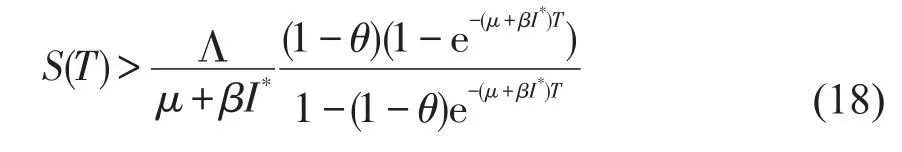
由（15）和（17），有

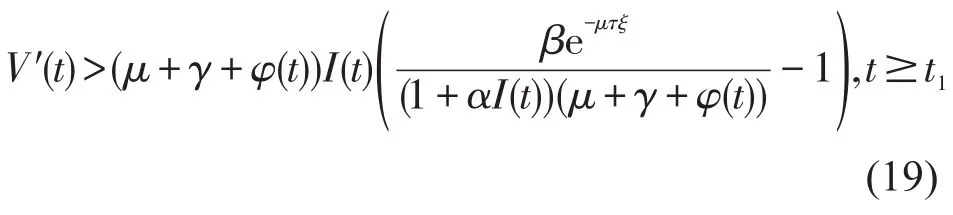
因为R*＞1，易得I*＞0进一步，则存在充分小的ε＞0使得

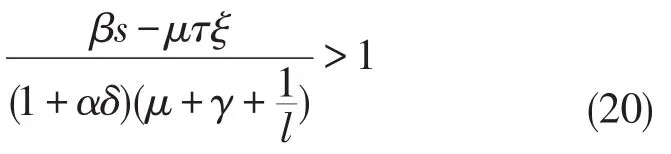
由上面的结果，可以得到

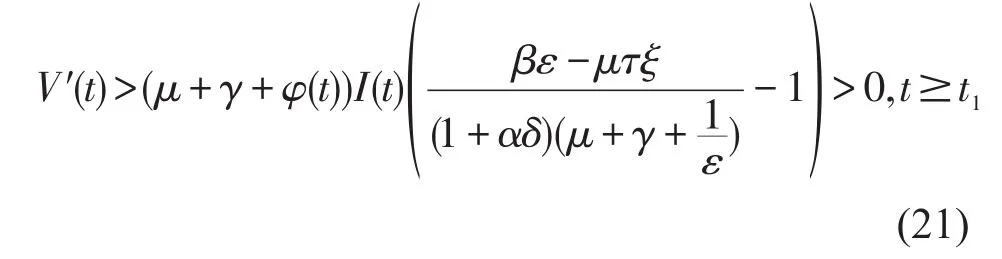
I(t)≥m,当t1≤t≤t1+τ+T*,I(t1+τ+T*)=m和I′(t1+τ+T*)≤ 0。

由系统（6）的第二个方程和（18），得

由（20）式 可 得I′(t1+τ+T*)＞0 ，这 和I′(t1+τ+T*)≤0。因此，I(t)≥m，当所有t≥t1，从（21）可得

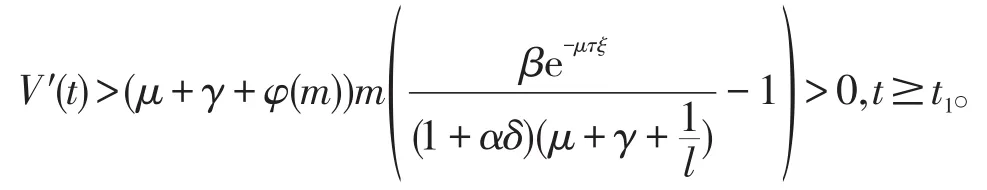
即V(t)→∞,t→∞。由（15）得相矛盾。因此，对任意t0＞0，不可能有I(t)＜I*，当所有t＞t0。

定理2如果R*＞1，则存在正常数P，使得系统（6）的任意解都满足I(t)≥P，当t充分大时。

证明基于定理的结论，从两个方面证明：

（i）I(t)≥I*，当t充分大时。

（ii）I(t)关于I*震荡，当t充分大时。

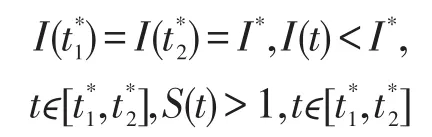
因为系统（6）的解是一致有界的，脉冲对I(t)没有影响，且是一直连续的，因此存在一个正常数k使得其中k满足k＜τ，且独立于和。设其 中p*=I*e-(μ+γ+φ(λ))。接下来讨论下面三种情形。

情形Ⅰ如果则很明显有I(t)≥k,时间t充分大时；

情形Ⅱ如果由系统（6）的第二个方程可得，I′(t)＞-(μ+γ+φ(I))I(t)。因为由比较定理可得

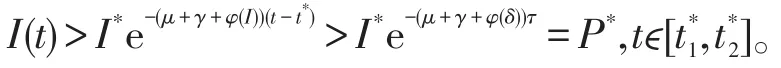
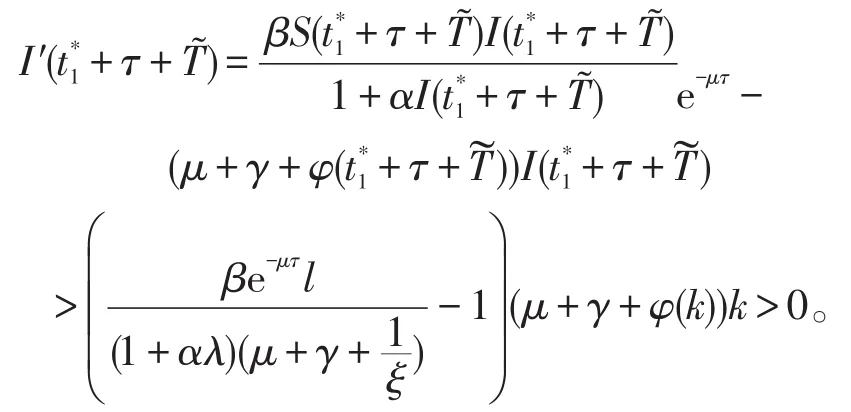
定理3如果R*＞1，系统（6）是持久的。

证明设(S(t),I(t))是系统（6）的任意解。由系统（6）的第一个方程可得

其比较方程为

ϵ1充分小。定义 Ω0={(S,I)|S≥M,I≥k,S+I≤λ}由上面的讨论和定理2，可以知道Ω0是全局吸引的且Ω0是正不变集。

4 结束语

系统（1）和系统（2）相比较，考虑了传染病的潜伏性，在时间上就体现为时滞，而脉冲接种和非连续治疗是预防和治疗常用的方法，在系统（2）中都有所体现。为了更接近真实情形，疾病的发生率我们采用了饱和发生率的形式。从定理1和定理3可以看出时滞τ和脉冲接种率θ对传染病的消亡有很大的影响，当潜伏时间越长，接种的次数越多传染病就越容易消亡，反之就容易形成地方性疾病。该结论可以为疾病控制等相关部门提供理论依据。

[1]许碧云，杨志春.对具有脉冲接种和分布时滞的SEIR传染病模型的定性分析[J].重庆师范大学学报（自然科学版）,2015,32(6):98-102.

[2]谢栋梁，卢金梅，李永凤.具有饱和发生率和时滞的脉冲SEIR模型分析[J].信阳师范学院学报(自然科学版),2016,29(4):490-493.

[3]Yuan Y,Zhao X Q.Global stability for non-monotone delay equations[J].Journal of Differential Equations,2012,252:2189-2209.

[4]Hou L L,Zong G D,Wu Y Q.Finite-time Control for Discrete-Time Switched Systems with Time Delay[J].International Journal of Control,Automation and Systems,2012,10(4):855-860.

[5]王寿斌，雒志学，王丽敏.具有连续预防接种和非线性传染率的SEIR传染病模型的稳定性分析[J].宁夏大学学报（自然科学版），2015,36(4):302-305.

[6]王寿斌，王丽敏，张 娣.一类具有脉冲接种和非线性传染率的SEIR传染病模型的分析[J].温州大学学报(自然科学版),2016,36(2):44-50.

[7]Zou Q,Gao S J,Zhong Q.Pulse Vaccination Strategy in an Epidemic Model with Time Delays and Nonlinear Incidence[J].Advanced Studies in Biology,2009,1(7):307-321.

[8]Xu X X,Xiao Y N,Robert A.Cheke.Models of impulsive culling of mosquitoes to interrupt transmission of West Nile virus to birds[J].Applied Mathematical Modelling,2015,39(13):3549-3568.

[9]Zhang T L,Kang R N,Wang K,et al.Global dynamics of an SEIR epidemic model with discontinuous treatment[J].Advances in Difference Equations,2015,2015:361-372.

[10]Gao S J,Chen L S,Juan J,et al.Analysis of a delayed epiemic model with pulse vaccination and saturation incidence[J],Vaccine,2006,24:6037-6045.

[11]Yang K.Delay Differential Equation with Application in Population Dynamics[M].New York:Academic Press,1993.

[12]Xiao Y N，Chen L S．Modeling and analysis of a predator-prey model with disease in the prey[J]．Mathematical Biosciences,2001,171(1):59-82．

Analysis of impulsive SEIR model with time delay and discontinuous treatment

FEI Li-zhia,LV Heng-minb,JI Wei-weib
(a.Normal College;b.Department of Basic Course Education,Ji'an College,Ji’an Jiangxi343000,China)

An impulsive SEIR epidemic model with time delay and discontinuous treatment was formulated and studied．Based on comparison theorem of impulsive differential equation,the research proves that the global attractive and the globally asymptotically stable of the disease free periodic solution.The thresholdR*andR*for disease to be extinct or not is calculated.IfR*＜1,the disease is extinct;IfR*＞1,the disease is permanence.Eventually,there will be endemic.

epidemic;time delay;pulse vaccination;permanence

O175.13文献识别码：A

1004-4329（2017）04-001-06

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）04-001-06

2017-09-12

吉安职业技术学院科研项目（16JY137）资助。

费荔枝（1982－ ），女，硕士，助教，研究方向：生物数学。