基于切比雪夫多项式的函数插值逼近

王先传 ，江 岩 ，赵 佳 ，张 岩

(阜阳师范学院 a.计算机与信息工程学院；b.数学与统计学院，安徽 阜阳 236037)

基于切比雪夫多项式的函数插值逼近

王先传a，江 岩b，赵 佳a，张 岩a

(阜阳师范学院 a.计算机与信息工程学院；b.数学与统计学院，安徽 阜阳 236037)

函数插值逼近经常应用于工程和技术领域。逼近效果不仅受算法影响，还与采用何种函数逼近有关。本文首先给出切比雪夫多项式的定义，讨论了其有关性质。而后重点论述了如何基于切比雪夫多项式的函数插值逼近，同时给出相应的Python语言代码。

插值逼近；Python；切比雪夫多项式；龙格现象

在许多工程和技术领域经常用到函数逼近、插值与拟合算法。除了最常用的最小二乘法，函数插值逼近方法还有构造有理函数[1]、神经网络[2]等。但这些方法实现起来比较复杂，而且比较效果也不够理想。另一方面，近年来切比雪夫多项式无论在理论还是在应用方面都也得到了较广泛的研究[3-8]。同时，伴随着数据科学的发展，Python语言也得到空前的发展。为此，本文将讨论如何基于切比雪夫多项式运用Python语言进行函数插值逼近。

1 Python简介

由Guido van Rossum 1989年发明的Python是一种解释型、面向对象、跨平台、动态高级编程语言[9]。随着大数据的发展，目前它已成为当今世界最受欢迎的计算生态语言。由于该语言简洁、易读、易学、好用，开设该语言的高校愈来愈多。

目前，比较流行的Python语言版本有Python 2.7和Python 3，但Python 3向下不兼容，即它是Python语言的现在和未来。为此，本文以它为平台进行相关编程。与Matlab不同，Python的开发环境有多种，如非集成开发环境有Anaconda和IPython Notebook等，集成开发环境有Spyder和PyCharm等。本文将以Anaconda为计算平台。

2 切比雪夫多项式

切比雪夫多项式是以俄国著名数学家切比雪夫(Tschebyscheff，1821-1894)命名的重要特殊函数，源于多倍角的余弦函数和余弦函数的展开式，分为第一类和第二类切比雪夫多项式。本文所用切比雪夫多项式属于第一类。

2.1 切比雪夫多项式的定义

切比雪夫多项式的定义如下：

定义1[10,11]称满足Tn(x)=cos(narccosx)，其中,n∈N,x∈R,且|x|≤1的{Tn(x)}为第一类切比雪夫多项式序列。Tn(x)称为第n个第一类切比雪夫多项式。令arccosx=θ，则cosθ=x。前8个第一类切比雪夫多项式如下：

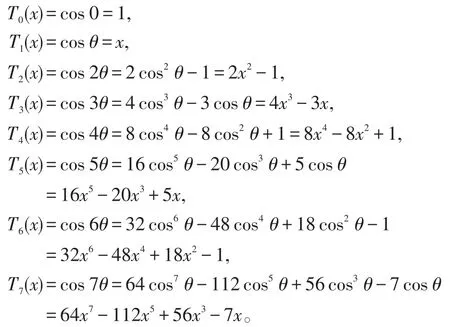
可以看出，它们都是最高项系数为2n-1、次数为n、系数符号正负相间、最小值为-1最大值为1的整系数多项式，其图像如图1所示。

2.2 切比雪夫多项式的性质

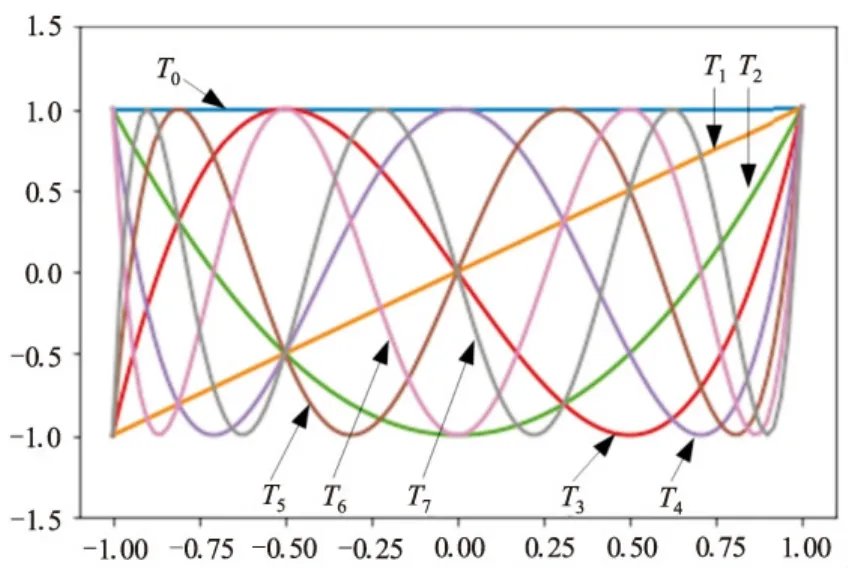
图1 0至7次切比雪夫多项式的图像

性质1[10,11](奇偶性)切比雪夫多项式满足

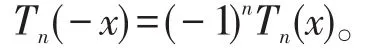
当n为偶数时，Tn(x)只含有x的偶次幂项，即Tn(x)为偶函数；当n为奇数时，Tn(x)只含有x的奇次幂项，即Tn(x)为奇函数。

性质2[10,11](递推公式)Tn(x)满足如下三个递推公式：

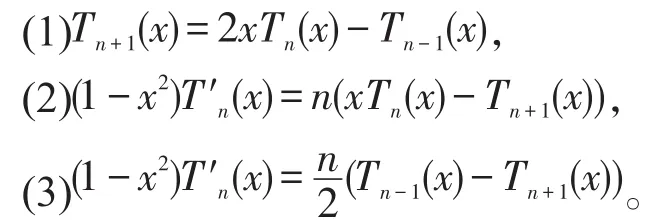
其详细证明请参见文献[10]。

性质3[10,11](零点)Tn(x)在区间(1,1)存在n个不同的零点，n＞0。这些零点为

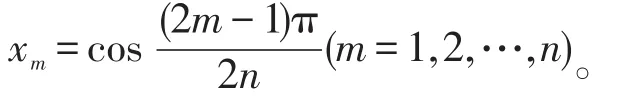
并称这些零点为切比雪夫节点。例如，在(1,1)内T1(x)=x有一个节点x=0；T2(x)=2x2-1有2个零点，即即本文正是利用节点进行多项式插值。

性质4[10,11](正交性)m≠n。即任意两个不同切比雪夫多项式之积在上的定积分等于0。

利用切比雪夫多项式的正交性，(-1,1)内的任意一个n次多项式f(x)可以表示为多个切比雪夫多项式的加权和，即其中

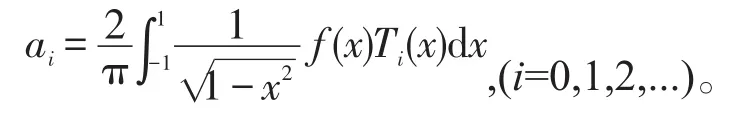
总之，切比雪夫多项式的这些特点表现了其独特的数学美，使它成为计算数学中重要函数。

3 基于切比雪夫多项式的函数插值逼近

下面运用Python语言，展示如何利用切比雪夫多项式实现函数插值逼近。

3.1 Anaconda下载、安装与测试

Anaconda是网页版Python语言编程环境。首先从https://www.continuum.io/downloads下载Anaconda。该网站提供 Windows、Linux和 Mac版的Anaconda软件，本文选择Windows版的Python 3.6版。而后完成软件安装并打开该软件。打开后运行Juyper，再选择New-＞Python 3。在In[]后的编辑框中输入1+2，而后同时按下Enter和Shift键运行程序，如果显示Out[1]及其后的运算结果为3，说明软件安装成功、测试结果正确。

3.2 切比雪夫节点与龙格现象

(1)导入必要的库和函数。如numpy库(用于科学计算)、pylab 库(用于作图)以及 Polynomial函数和Chebyshev函数。

(2)定义待逼近的函数。

(3)定义切比雪夫多项式次数，并计算其节点即插值取样点。

(4)调用Chebyshev的fit函数生成插值点的函数值。

(5)计算最大误差。

(6)绘制插值和逼近结果。

从结果可以看出采用等间隔取样点进行函数插值的最大误差为2.3536，而采用切比雪夫节点进行函数插值的最大误差为0.1175。

插值结果如图3所示，可以看出，采用等间隔插值时插值多项式的两端有非常大的震荡。该现象被称为龙格现象，n越大龙格现象越明显。而采用非等间隔的切比雪夫节点插值时插值多项式的龙格现象明显减少，而且n越大龙格现象越小。

图2 展示切比雪夫节点和龙格现象的Python程序

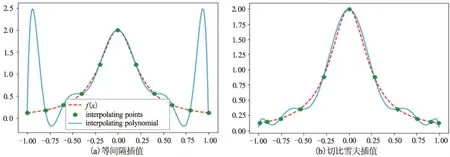
图3 Polynomial函数和Chebyshev函数的插值结果及其龙格现象

3.3 切比雪夫插值与一般多项式插值比较

由3.2节可知，切比雪夫多项式进行函数插值的误差比一般多项式要小许多，而且插值的整体效果也好。下面用一个例子来说明切比雪夫插值的优势。

对g(x)=sin 25(x-1)2+sin32(x-2)在100个切比雪夫节点上分别用Python的Polynomial和Chebyshev插值，程序如图4所示。可以看出，二者的区别仅在于计算插值点函数值时所用的函数不同。运行程序时，使用Polynomial进行插值时会发生“RankWarning:The fit may be poorly conditioned”警告。也就是说使用该方法进行该函数的插值拟合，结果不理想，如图5所示。可以看出，用Polynomial插值时所得多项式不能经过所有插值点，而使用Chebyshev进行插值时所得多项式经过所有插值点。两种不同插值的最大误差分别为1.1951和6.4757×10-9。结合图4可知，其原因只是在于进行插值时所采用的插值方法不同。

图4 Polynomial函数和Chebyshev函数插值的Python代码

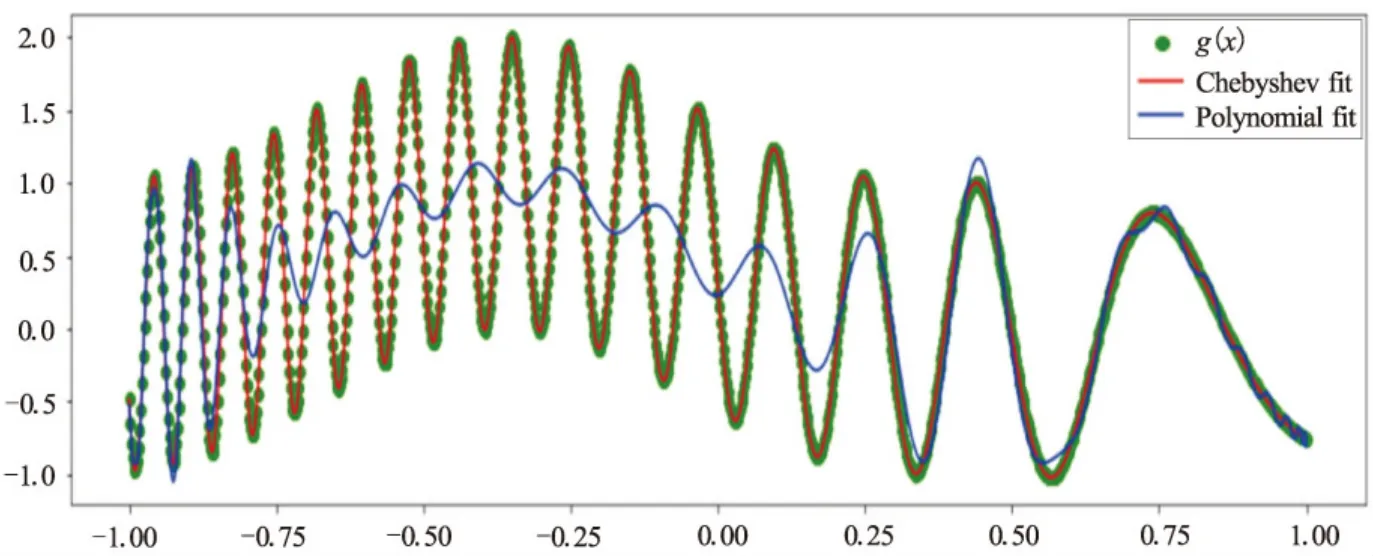
图5 Polynomial函数和Chebyshev函数的插值结果

3.4 一般区间函数的插值逼近

如前所述，切比雪夫多项式是定义在区间[-1,1]上的正交多项式，因此只有在该区间才能对待逼近函数进行正确插值逼近。为对任意区间上的函数都能正确插值逼近，需要对待插值区间进行放缩和平移变换。在Python语言中可通过参数domain指定待插值区间。例如对在区间[-8,2]上采用切比雪夫多项式插值逼近。其相关代码如图6所示，需要注意的是要将Chebyshev的basis和fit函数中的domain参数都设置为区间[-8,2]，同时linspace函数也要指定在该区间上。n分别取20,40,60和80对h(x)进行插值逼近时的运行结果如图7所示。可以看出，n值越大，插值逼近效果越好。但n越大计算量也就越大。因此n的选择需要根据具体情况而定。

4 小结

本文首先简单介绍了Python语言，而后给出了切比雪夫多项式的定义，讨论了其奇偶性、正交性等性质。在此基础上，详细讨论了如何基于切比雪夫多项式在区间[-1,1]上进行函数插值逼近，对采用一般多项式插值逼近和切比雪夫多项式插值逼近进行了比较，最好讨论了如何对定义在一般区间上的函数进行插值逼近。结果表明切比雪夫多项式插值逼近明显优于等间隔插值逼近和一般多项式插值逼近，而且所用切比雪夫多项式次数越高，逼近效果越好。同时，也可以看出使用Python语言处理函数插值逼近这样复杂问题的简洁性。

图6 一般区间上的Chebyshev函数插值逼近Python代码

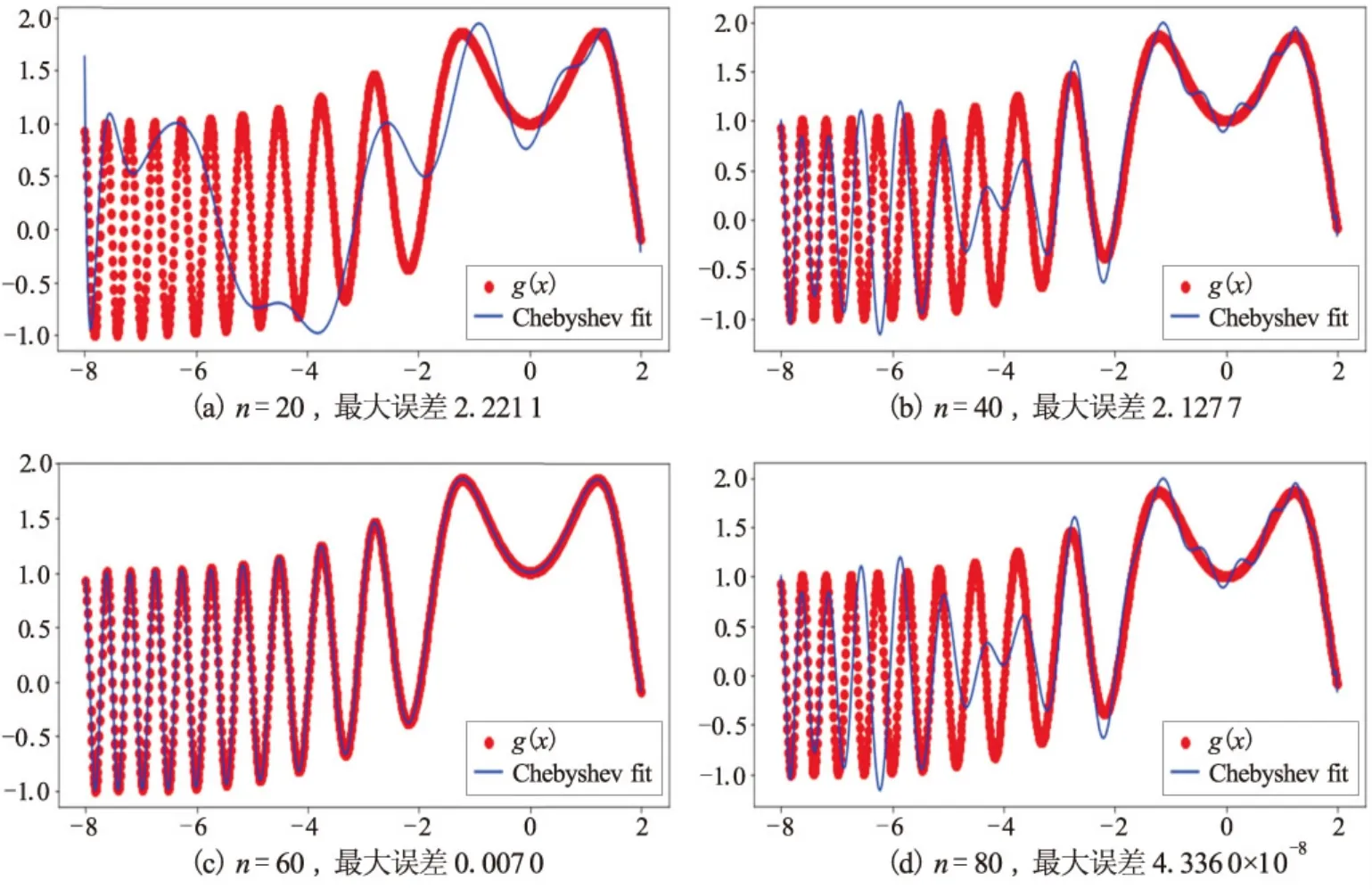
图7 不同n值对一般区间上Chebyshev函数插值逼近的影响

[1]孙定浩，赵长春.构建有理函数逼近式的一种新方法[J].空间控制技术与应用，2016，42（1）：57-62.

[2]岑红蕾，鲁 敏，聂 晶.基于BP神经网络的非线性函数逼近仿真研究[J].农业网络信息，2015（1）：52-55.

[3]凌明灿，吴 康.第一类切比雪夫多项式方程的重根规律[J].五邑大学学报(自然科学版)，2013，27（2）：13-15.

[4]傅 翀，雷 斌，韩 冰，等.基于切比雪夫多项式的HRWS星载SAR成像算法[J].国外电子测量技术，2015，34（8）：40-46.

[5]侯育星，陈士超，唐 禹，等.基于切比雪夫多项式的新形式调频变标合成孔径雷达成像算法[J].电子与信息学报，2014，36（11）：2646-2651.

[6]刘 亮.有限域切比雪夫多项式算法性能测试与分析[J].中国传媒大学学报(自然科学版)，2012，19（4）：54-58.

[7]Rajesh K P,Suraj S,Koushlendra K S,et al.An approximate method for Abel inversion using Chebyshev polynomials[J].Applied Mathematics and Computation,2014,237(15):120-132.

[8]Mesk M,Zahaf M B.A new characterization of ultraspherical,Hermite,and Chebyshev polynomials of the first kind[J].Journal of Mathematical Analysis and Applications,2017,448(2):1147-1162.

[9]张若愚.Python科学计算[M].2版.北京：清华大学出版社，2016：1-5.

[10]刘式适，刘式达.特殊函数[M].北京：气象出版社，1988：304-320.

[11]Mason J C,Handscomb D C.Chebyshev polynomials[M].New York:CRC Press Company,2003:1-50.

Function interpolation and approximation based on Chebyshev polynomials

WANG Xian-chuana,JIANG Yanb,ZHAO Jiaa,ZHANG Yana
(a.School of Computer and Information Engineering;b.School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui236037，China)

Function interpolation and approximation is often applied to engineering and technology.The approximation effects are affected not only by algorithms but also by adopted functions.This paper introduces Chebyshev polynomials and their properties.And then it focuses on discussing how to approximate a function based on Chebyshev polynomials.Meanwhile,it also shows the relevant codes in Python.

interpolation and approximation;Python;Chebyshev polynomials;Runge phenomenon

O174文献识别码：A

1004-4329（2017）04-007-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）04-04-007-05

2017-09-12

国家级大学生创新项目（201610371010）；阜阳师范学院质量工程项目（2014JXTD01）；阜阳师范学院横向课题（XDHX2016021）；阜阳师范学院校级重点科研（2017FSKJ05ZD）资助。

王先传（1983－ ），男，博士，讲师，研究方向：数据挖掘、自然语言处理。