一类和式极限的求法

李建丽，张文娟

（长治学院 数学系，山西 长治 046011）

一类和式极限的求法

李建丽，张文娟

（长治学院 数学系，山西 长治 046011）

采用对区间进行等比分割的方法，并取小区间的端点或等比中项，将一类和式极限转化为定积分来计算，进一步，将此方法推广到矩形区域上，将和式极限转化为二重积分来计算，并通过实例加以应用。

等比法；和式极限；定积分

1 预备知识

极限问题的研究是数学中一直以来讨论的话题，尤其是和式极限，到目前为止还没有一个统一的方法，文献[1-3]研究了几类特殊和式极限的计算方法。我们知道，极限方式定义了定积分，反过来定积分又在求极限的过程中扮演着重要的角色，利用积分求极限是解决极限问题的一种重要方法，特别是一般项由和式表达的极限。

众所周知，定积分是一类和式极限[4]

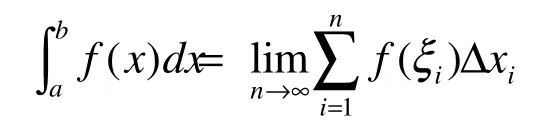
其中△xi（i=1，2，…，n）是对[a，b]的任意分割，ξi∈△xi是任取的点。

在函数连续的条件下，对[a，b]采取n等分分割，得到：

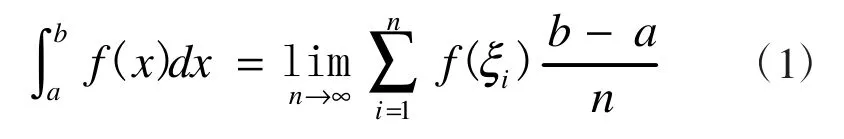
这类极限的基本的特征是△xi中没有i的表达式，即△xi与求和运算可交换顺序[5]，例：经过简单变形可转化为定积分来计算。

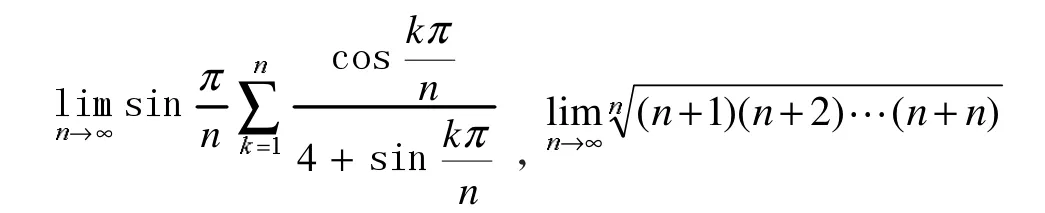
由于定积分是对区间任意的分割，在每个分割的小区间上任意的取点，在可积条件下，无论怎样分割和怎样取点，和式具有相同的极限。这就使得定积分可以表示成不同形式的和式极限，但反过来，对于一个较为复杂的和式极限，从直观上难以判断是如何对区间作的分割，从而很难将其转化为定积分计算。文章主要介绍一类具有某种特征的和式极限，并将其转化为定积分。

2 主要结果

2.1 分割区间

设f（x）是定义在[a，b]（a＞0）上的连续函数，在[a，b]上插入n-1个分点：

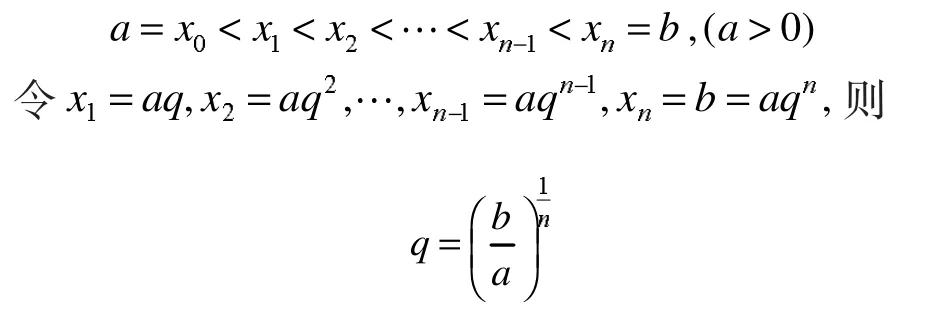
这些点将[a，b]分成n个区间

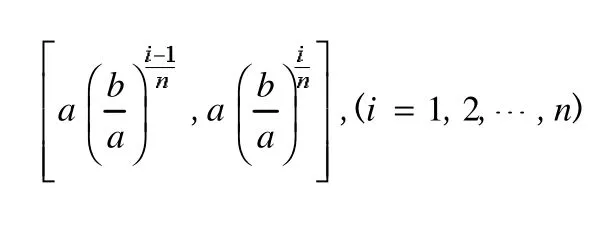
在每个△xi上，若ξi取右（左）端点或等比中项，则f（x）的定积分可以写为：

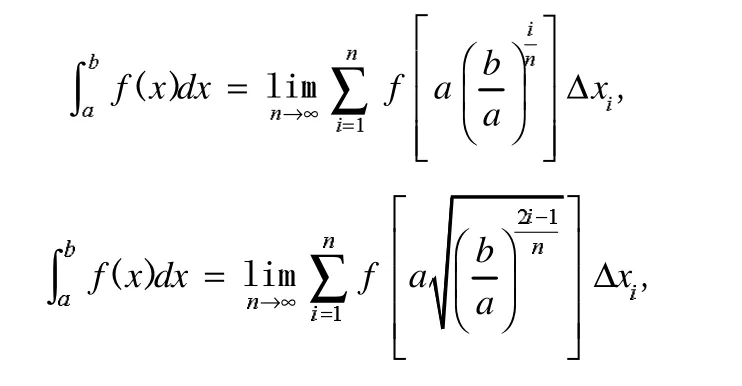
我们看到等式右边是一个和式极限，但△xi不能与求和运算交换顺序，对于这类极限我们可以借助于定积分的定义进行计算。

例1 计算

2.2 分割区域

设f（x，y）是定义在矩形区域D=[a，b]×[c，d]（a，c＞0）上的连续函数，将D进行分割∶

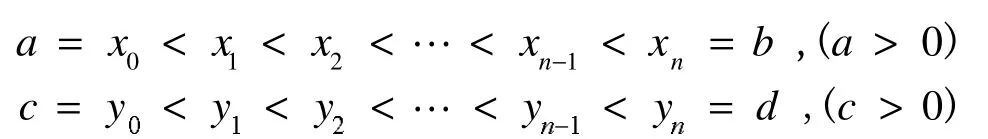
作法类似于以上基本思想，

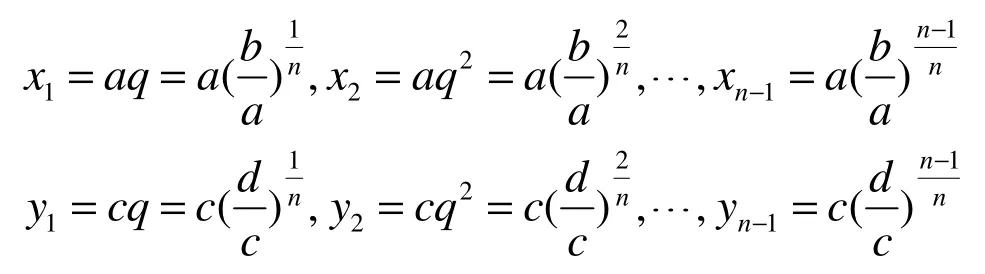
这些直线将D分成n2个小矩形Δσij=[xi-1，xi][yj-1，yj]（i=1，2，…，n；j=1，2，…，n），若分别取

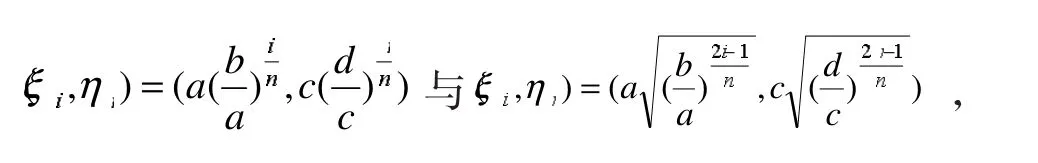
可以将和式极限转化为二重积分计算。

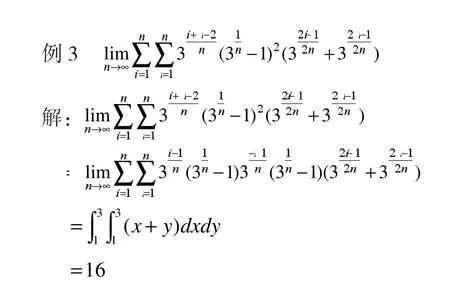
综上，利用积分的定义求和式极限的关键是∶寻找被积函数，确定积分的上限和下限，从而运用等比法求解和式极限。

［1］王良成.用等价无穷小替换求一类和式极限［J］.大学数学，2013，（3）：97-100.

［2］陈思源.求解一类和式极限的新方法［J］.河南科学，2012，（3）：278-280.

［3］王海祥.一类和式极限问题的初等解法及推广［J］.高等数学研究，2002，（3）：57-58.

［4］华东师范大学数学系.数学分析(上)［M］.北京:高等教育出版社，2010.202-223.

［5］裴礼文.数学分析中的典型问题与方法［M］.北京:高等教育出版社，2006.304-320.

O171

A

1673-2014（2017）05-0069-02

山西省高等学校大学生创新创业训练项目（2017437）；山西省高等学校教学改革创新项目（J2016111）

2017—06—12

李建丽（1983— ），女，山西高平人，讲师，硕士，主要从事基础数学方面的研究。

（责任编辑 赵巨涛）