具有弹性支承输流管路的振动分析

2018-01-04赵千里孙志礼柴小冬

振动、测试与诊断 2017年6期

关键词：层流固有频率管路

赵千里，孙志礼，柴小冬

(东北大学机械工程与自动化学院沈阳,110819)

具有弹性支承输流管路的振动分析

赵千里，孙志礼，柴小冬

(东北大学机械工程与自动化学院沈阳,110819)

为研究截面内流速不均以及弹性支承对输流管路振动问题的影响，利用伽辽金法对考虑了流动模型修正因子的具有弹性支承的两端固定式输流管路的振动微分方程进行了推导，得到了一般形式下输流管路强迫振动稳态响应的表达式。结果发现：流动形式为层流时管路的固有频率和临界流速均小于理想流动模型(平推流模型)的值；前者的发散临界流速比后者小约13.4%，与理论结果一致；固有频率随弹簧安置位置的增加而呈现振荡的变化，但始终大于无弹性支承时的值。该方法可作为设计支承形式的基础，可以推广用来研究其他类型管路的振动问题，并为设计人员提供精确的计算结果。

伽辽金法；自由振动；强迫振动；输流管路；流动模型修正因子

引言

输流管路是能够输送流体介质的所有类型管路的统称。在工业技术发达的现代社会，输流管路是许多生产生活过程中必不可少的关键部分，如城市的供热系统、天然气和石油的运输系统、液压油的传送装置等。在使用过程中，受使用环境(载荷、温度、湿度等)影响，各类管路会发生不同的失效现象，如跑冒滴漏、塑性变形甚至断裂等。输流管路的流固耦合振动是导致上述失效模式的主要原因之一，关于输流管路的流固耦合振动问题受到了学者的广泛关注并出版了大量的研究结果[1-5]。文献[1]指出，输流管路的流固耦合振动已经成为一类典型的动力学问题，关于这类问题的研究目前主要分为理论模型和求解方法两个方向。通常来讲，建立输流管路的力学模型时均以梁模型为理论基础，然而，由于流体与管路内壁之间黏性的存在，同一横截面内的流速并非处处相同。在文献[6]中，流动模型修正因子这一参数被引入到输流管路的流固耦合振动问题中。文献[7]对考虑了修正因子的小尺度输流管路的流体诱发振动问题进行了深入的研究。

在求解方法的研究方面，典型的方法主要包括有限单元法[8]、传递矩阵法[9]、微分变换法[10]、微分求积法或其广义形式[11]以及格林函数法[12]等。各方法均有其优势的使用范围，如文献[10]中利用微分变换法求解了悬臂式、两端固定式、固定-简支式以及两端简支式这4类典型的输流管路的固有频率随流速的变化关系。文献[12]利用格林函数法计算得到了输流管路线性非齐次形式的强迫振动微分方程的解析解。

实际上，两端安装固定夹的输流管路可近似视为文献[7]中所述的两端固定式，而对于跨度较大的情况，需要在两固定端的中间再添加弹性支承以控制振动的幅度。因此，笔者在考虑了流动模型修正因子的基础上，利用伽辽金法推导了中间具有弹性支承的两端固定式输流管路的自由和强迫振动微分方程，得到了自由振动下固有频率以及强迫振动下位移响应的表达式，重点研究了修正因子和弹性支承对管路流固耦合振动问题的影响。

1 力学模型及振动微分方程

具有弹性支承的两端固定式输流管路的强迫振动力学模型如图1所示，其中L为管路的长度。

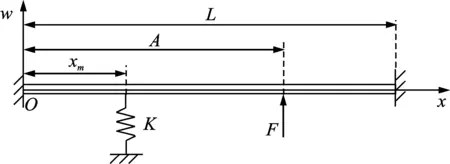
图1 输流管路的力学模型Fig.1 Mechanical model of fluid conveying pipe

对图1所示的力学模型，其完整的线性振动微分方程参见文献[1]，笔者仅研究修正因子及弹性支承对这类管路振动问题的影响。为了简化问题，忽略了重力、张力、内部压力及阻尼等因素，仅考虑小变形情况。依据牛顿第二运动定律，以单位长度的管路为研究对象，可以得到其运动微分方程为

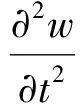
(1)

其中：EI为管路的弯曲刚度；w为横向挠度；x和t分别为位置坐标和时间；α为流动模型修正系数；M和m分别为单位长度流体和管路的质量；U为横截面内流体的平均流速；K为弹簧的弹性系数；xm为弹簧的安置位置；F为外载荷。

为便于研究，可定义其无量纲形式为

kηδ(ξ-ξm)=f(ξ,τ)

(2)

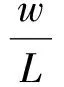
假设管路承受关于时间简谐的激励，则可将式(2)写为

kηδ(ξ-ξm)=f(ξ)eiωτ

(3)

如无特殊说明，下面所有的研究均采用无量纲形式的参数。

2 输流管路振动问题的伽辽金表达式

2.1 伽辽金方法在本研究中的应用

伽辽金法属于加权余量法的一种，令有限项形函数的和在求解域及边界上的加权积分满足原方程，其中加权函数为形函数本身，即可得到一组易于求解的线性方程。

根据伽辽金法的定义，式(3)的解可近似表示为

(4)

其中：N为形函数的个数；φn为形函数；qn为时间相关项。

将式(4)代入式(3)，可得

(5)

分别将各形函数与式(5)相乘并将结果关于ξ在区间[0,1]内积分，经过整理可得

(6)

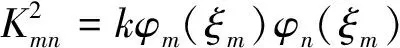
经过整理，式(6)可以表示为

(7)

对于如图1所示的两端固定式输流管路，其无量纲边界条件为

(8)

形函数必须使式(8)始终成立。一般来讲，应用伽辽金法研究梁或输流管路的振动问题时，形函数均是采用梁的振型函数[13-14]，其表达形式过于复杂，在本研究中，将形函数选为

φn(ξ)=anξn+1(1-ξ)2(n=1,2,…,N)

(9)

式(8)的边界条件得以满足，an可以通过归一化条件求得，即

(10)

通过化简，可得

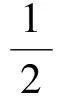
(11)

经过整理，形函数向量可表示为

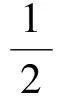
{3·4·5·ξ2,…,(N+2)(N+3)(N+4)ξN+1}T

(12)

2.2 强迫振动问题的解

假设管路承受如式(3)中定义的简谐激励，则可假设式(7)的稳态解的形式为

q=q0eiωτ

(13)

将式(13)代入式(7)，通过化简可以得到

q0=(-ω2M+iωG+K)-1Fe-iωτ

(14)

因此，输流管路在时域内的稳态响应为

η(ξ,τ)=Re{φ(-ω2M+iωG+K)-1F}

(15)

3 计算结果与分析

3.1 方法的有效性

假设管路承受集中的简谐激励，则式(3)中的f(ξ)可表示为

f(ξ)=f0δ(ξ-a)

(16)

其中：a为激振位置的无量纲形式，且a=A/L。

外载荷向量F可表示为

F=f0eiωτ{φ1(a),φ2(a),…,φN(a)}T

(17)

将式(17)代入式(15)便可计算出输流管路的时域响应。取f0=5.0，a=0.5，ω=20.0，u=1，α=1，β=0.5，并用ηmax表示挠度的幅值，分别利用格林函数法和本方法计算ξ=0.8处的ηmax，结果见表1。

表1 输流管路的挠度幅值(ξ=0.8)

由表1可知，当N=8时，本方法与格林函数法的解已经十分相近，随着N的增加，本方法的计算结果将无限接近精确解。综合考虑计算精度和计算效率，下面的计算均取N=8。

3.2 无弹性支承输流管路的横向振动问题

首先研究系统的固有频率。令式(7)中的外载荷向量等于0，即可得到系统的自由振动微分方程，此时的特征方程为

(ω2MN×N+ωGN×N+KN×N)qN×1=0

(18)

其中：ω为无量纲固有频率，其形式与式(3)中定义的相同。

令系数矩阵的行列式等于0便可得到固有频率的解。根据文献[6]的分析，当管路内部流体的流动形式为平推流时，α=1，当流动形式为层流时，α=4/3≈1.333且发散临界流速ucd的理论解为

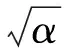
(19)

其中：μ为与管路支承形式相关的长度系数，对于两端固定式输流直管，μ=0.5。

由式(19)可知，管路的临界流速仅与μ和α有关，与其他因素无关。图2为输流直管的前4阶固有频率随流速的变化关系，同一线型由下向上的4条曲线分别代表前4阶固有频率，其中虚线代表层流模型的解，实线代表平推流模型的解。由图可知，对于前者，ucd=5.441，理论解为5.441；而对于后者，ucd=6.283，理论解为2π，前者比后者小约13.4%，计算结果与理论解几乎相同，证明本方法十分精确，同时说明了在同等参数的条件下，层流模型下的管路在较低流速下容易失稳。事实上，通过计算可得，前者的1,2阶模态耦合颤振的临界流速值ucf=8.049，后者的结果则为ucf=9.295，前者比后者同样小约13.4%。

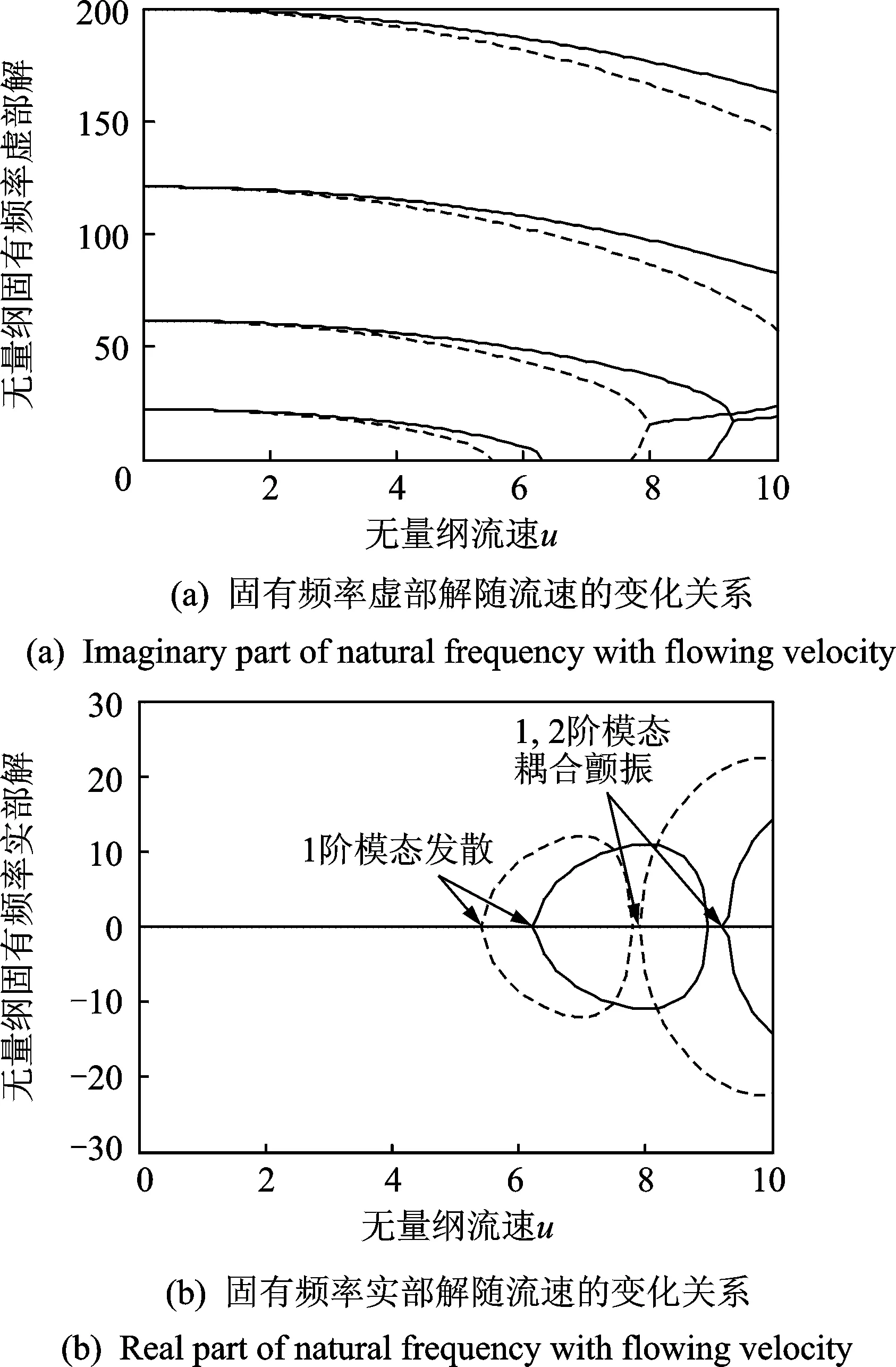
图2 固有频率随流速的变化关系(β=0.5)Fig.2 Natural frequency with flowing velocity (β=0.5)

上述计算表明，用平推流模型近似流体在管路内的流动所得的结果与层流模型相差较大，这种差别对强迫振动响应的计算会产生较大的影响。例如：取f0=5.0，a=0.5，ω=20.0，u=1，β=0.5，利用本方法计算这两类流动模型下的振动幅度随流速的变化关系，结果如图3所示。

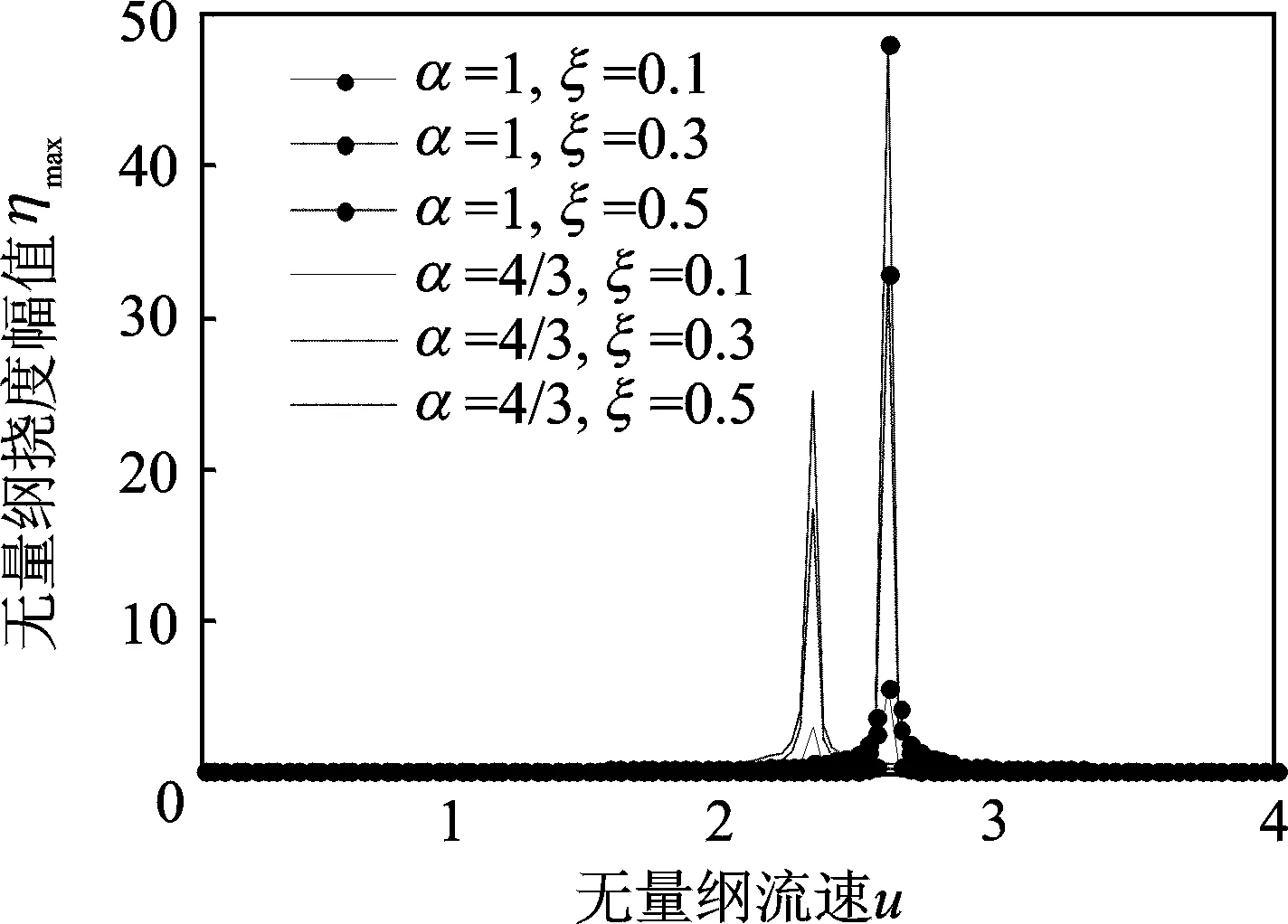
图3 挠度幅值随流速的变化关系Fig.3 Amplitude of deflection with flowing velocity

由图3可知，层流模型下的振动幅值明显较平推流模型下的幅值小，意味着依据后者计算结果的设计是偏向于安全的。

3.3 具有弹性支承输流管路的横向振动问题

本节主要研究弹性支承对管路自由及强迫振动的影响，显然，问题为非线性，格林函数法不再适用。采用与3.2节相同的方式可得到弹性支承下的临界流速值，其与弹性系数的关系如表2所示。

表2临界流速与弹性系数的对应关系(ξm=0.3)

Tab.2Correspondingrelationshipbetweencriticalvelocityandelasticcoefficient(ξm=0.3)

kucd(α=1)ucd(α=4/3)偏差/%1016．3515．5001026．8445．92713．41037．8396．7891048．0186．9441088．0386．961

由表2可知，弹性系数增加仅仅使得式(19)中的μ减小，因此导致临界流速增加，两种流动模型的临界流速之间的偏差仍大约为13.4%。当k趋近于无穷大时，临界流速趋于定值，系统可视为由两段固定-简支式管路组合而成。平推流模型与层流模型的计算结果差异较大，然而在实际应用中，大多数情况下的流动均为层流，因此，以下的研究全部基于层流模型的考虑。

由于所研究管路的两端支承形式相同，所以在计算固有频率时可以仅计算ξm∈[0,0.5]区间内的值，另一半区间内的结果只需关于ξm=0.5取对称即可。管路的前4阶固有频率随弹簧的弹性系数及其安置位置的变化关系如图4所示。

图4 固有频率随弹性支承的变化关系(u=1，β=0.5)Fig.4 Natural frequency with elastic support (u=1，β=0.5)

同一线型由下向上的4条曲线分别代表前4阶固有频率。如图4所示，固有频率随着弹簧安置位置的变化呈现振荡的变化，且弹性系数越大，振荡的幅度越大，但是无论怎样变化，在给定安置位置下，管路的固有频率始终随弹性系数的增加而增加。

为了研究弹性支承对管路受迫振动响应的影响，取f0=5.0，a=0.5，u=1，β=0.5，可计算得到ξ=0.8处的挠度幅值随弹性支承的变化。

由图5(a)可知，由于在所研究的弹性支承范围内激振频率并没有等于固有频率，所以管路不会发生共振。挠度幅值随弹性系数或安置位置的增加均有所下降，说明弹性支承有效地抑制了振动。在图5(b)中发现，当k分别等于103和104时，挠度幅值曲线上均出现了峰值，依据共振原理可知，峰值出现的位置对应的固有频率必然等于激振频率75.0，这一结论也可由图4得到，说明添加弹簧的同时也增加了管路发生共振的可能。

图5 挠度幅值随弹性支承的变化关系Fig.5 Amplitude of the deflection with elastic support

为了抑制输流管路受迫振动的幅度，在对管路进行设计的时候需要分别从弹性支承和外部激励两方面考虑,即激励确定的情况下，必须合理搭配弹性系数及弹簧的安置位置，而在弹性支承给定的情况下，激振频率需控制在一定区域内，弹簧的添加进一步限制了激振频率的范围。更深层次来说，若两个因素都不确定，则要通过优化设计进行合理地分配参数。这就凸显了本方法的重要性，因为它可以在其他给定数据的基础上计算出可信的数据以供设计人员参考，这样不仅可以有效地避免共振的发生，更能使振动控制在需要的范围内，因此，本方法可以有效地提高设计效率以及管路系统的可靠性。

4 结论

1) 利用伽辽金法推导得到了考虑流动模型修正因子并具有弹性支承的两端固定式输流管路面内自由振动的特征方程及强迫振动的稳态响应，分别得到了计算固有频率及稳态响应的表达式。

2) 分析了层流模型下具有弹性支承输流管路的自由及强迫振动问题，研究发现，相比于平推流模型，层流模型时管路的固有频率和临界流速均小于前者；固有频率随弹簧安置位置的增加而呈现振荡的变化，但始终大于无弹性支承的值。

3) 所提方法可为设计人员提供精确可信的数据，有效地减少了设计人员的工作量，为后续的可靠性设计等内容作了良好的铺垫。

[1] Paidoussis M P，Li G X. Pipes conveying fluid: a model dynamical problem[J]. Journal of Fluids and Structures，1993，8：137-204.

[2] 张晓伟，李苏洋. 空调管路系统的振动分析[J]. 振动、测试与诊断，2012，32(S1)：120-122.

Zhang Xiaowei，Li Suyang. Vibration analysis of air condition pipes[J]. Journal of Vibration, Measurement & Diagnosis，2012，32(S1)：120-122. (in Chinese)

[3] Kutin J，Bajsic I. Fluid-dynamic loading of pipes conveying fluid with a laminar mean-flow velocity profile[J]. Journal of Fluids and Structures，2014，50：171-183.

[4] Stephanie E，Thomsen J J. Predicting phase shift effects for vibrating fluid-conveying pipes due to coriolis forces and fluid pulsation[J]. Journal of Sound and Vibration，2011，330：5096-5113.

[5] 姜宏伟，袁朝辉，邱雷. 运用小波变换的飞机管路振动信号降噪方法[J]. 振动、测试与诊断，2012，32(5)：827-831.

Jiang Hongwei，Yuan Chaohui，Qiu Lei. Wavelet transform based denoising method on pipe vibration signals of aircraft[J]. Journal of Vibration, Measurement & Diagnosis，2012，32(5)：827-831. (in Chinese)

[6] Guo Changqing，Zhang Chuhan，Paidoussis M P. Modification of equation of motion of fluid-conveying pipe for laminar and turbulent flow profiles[J]. Journal of Fluids and Structure，2010，26：793-803.

[7] Wang Lin，Liu Hongtao，Ni Qiao，et al. Flexural vibrations of micro-scale pipes conveying fluid by considering the size effects of micro-flow and micro-structure[J]. International Journal of Engineering Science，2013，71：92-101.

[8] Misra A K，Paidoussis M P，Van K S. On the dynamics of curved pipes transporting fluid, part II: extensible theory[J]. Journal of Fluids and Structures，1988，2：245-261.

[9] Li Shuaijun，Liu Gongmin，Kong Weitao. Vibration analysis of pipes conveying fluid by transfer matrix method[J]. Nuclear Engineering and Design，2014，266：78-88.

[10] Ni Qiao，Zhang Zilong, Wang Lin. Application of the differential transformation method to vibration analysis of pipes conveying fluid[J]. Applied Mathematics and Computation，2011，217：7028-7038.

[11] 李威，曾志松，韩旭. GDQR求解弹性地基上输流管道的稳定性[J]. 振动与冲击，2015，34(4)：211-215.

Li Wei，Zeng Zhisong，Han Xu. Stability of pipes conveying fluid on an elastic foundation based on GDQR[J]. Journal of Vibration and Shock，2015，34(4)：211-215. (in Chinese)

[12] Li Yundong，Yang Yiren. Forced vibration of pipe conveying fluid by the Green function method[J]. Archive of Applied Mechanics，2014，84：1811-1823.

[13] 金基铎，杨晓东，邹光胜. 两端支承输流管道的稳定性和临界流速分析[J]. 机械工程学报，2006，42(11)：131-136.

Jin Jiduo，Yang Xiaodong，Zou Guangsheng. Stability and critical flow velocity of supported pipes conveying fluid[J]. Chinese Journal of Mechanical Engineering，2006，42(11)：131-136. (in Chinese)

[14] 周奇郑，王德石，平子鹏. 非线性支撑下悬臂输流管道的Hopf分叉特性[J]. 海军工程大学学报，2015，27(1)：26-30.

Zhou Qizheng，Wang Deshi，Ping Zipeng. Hopf bifurcations of nonlinear support cantilever fluid- conveying pipeline[J]. Journal of Naval University of Engineering，2015，27(1)：26-30. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.023

国家科技重大专项课题资助项目(2013ZX04011-011)

2016-10-12；

2016-12-12

TH137； O327