一道例题的多视角探究

江苏省苏州工业园区第二高级中学 (215121)

南爱玲

一道例题的多视角探究

江苏省苏州工业园区第二高级中学 (215121)

南爱玲

著名数学家波利亚在其著作《怎样解题》中给出一张解题表，包括弄清问题，拟定计划，实现计划，回顾.弄清问题就是我们通常说的审题，分析理解题目中的条件，研究问题的结论；拟定解题方案，这一过程中要有理性思维，分析解决问题需要的条件，如何实现与已知条件之间的转化；实现计划，就是具体解决问题的过程，在解题过程中不断调整策略；回顾，就是解题后进行总结和反思，完善解题认知结构.而解题教学时数学课堂的一个重要组成部分，教师不仅要教会学生怎样解题，还应该探究数学思维的过程，解题后养成回头看一看的习惯，也就是我们通常所说的解题反思，反思解决问题的方法和思路.本文遵循波利亚的解题步骤，从不同的视角对一道典型例题进行探究.

一、弄清问题，高屋建瓴

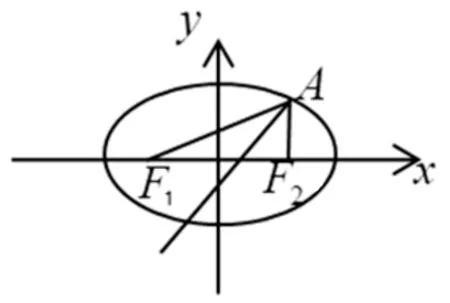
图1

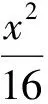
审题是解题的首要环节，深入细致的审题是顺利解题的前提，因此在平时的解题教学中，要引导学生重视审题.

审题就是要弄清楚题目的背景，分析题目中的已知条件，弄清要解决的问题.这是一道求直线方程的问题，直线的方程在江苏省考试说明中是C级要求内容，要求系统地掌握知识的内在联系，并能解决综合性较强或较为困难的问题.本题以椭圆为背景，给定椭圆上一定点A(2,3)，求两个焦点F1,F2对点A张角的平分线，从难易程度上来讲，属于基础题，但是判断一道题好不好，难易不是唯一的标准，还要看这道题是否典型，是否包含了重要的基础知识，解题过程中是否能够多角度探究，培养学生的思维能力，从这个角度看，本题很典型.因为题目中椭圆的方程已知，可以求出椭圆两焦点F1,F2的坐标，而这个角平分线所在直线必经过点A，那么要求该直线的方程，只要再求出直线上一点坐标或者求出该直线的斜率即可.

二、拟定计划，深谋远虑

拟定计划也就是根据题目中的条件探究解题思路的过程.求直线的方程这种题型对学生来讲是一类常见题型，在读完题目后学生的思路应该就出来了，两类思路：只要再求出直线的另一点的坐标或者求出直线的斜率.第一种思路中要考虑的问题是求哪一点的坐标呢？我们可以考虑该直线与x轴或者y轴的交点，当然也可以任意取一点P(异于点A)，根据角平分线的性质：角平分线上的点到角的两边距离相等，即可求出点的坐标，问题也就随之解决.而第二种思路中求直线的斜率，相对来讲思维难度要大一点.那么这时候要考虑的问题就是求斜率的方法有哪些呢？本题中哪些方法可行？顺着这个思路寻求问题的解决办法.这是一道比较简单的求直线问题，在实际教学中，有的老师处理这个问题时可能一带而过，那就很遗憾了，没有从各个视角深入探究这个问题，也就错失了利用这道题拓展学生的视野，培养学生分析问题解决问题的能力.

三、实施计划，灵活应变

(一)求点

(1)特殊点的视角

在求点时往往选择直线与坐标轴的交点，原因是坐标轴上的点有一个坐标为0，可以简化运算.这其实也是特殊化的具体应用，特殊化是数学解题教学中尤其是解析几何中应用较为广泛，通过对某种特殊位置的考察，来探究一般情况的性质.

(2)直线方程的定义视角

所谓求直线的方程，其本质就是求直线上任意一点P(x,y)的纵坐标y与横坐标x之间满足的关系.如果从这个角度考虑，我们就可以根据角平分线的性质直接求出直线的方程.

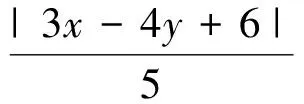
(3)角平分线定理的视角

除了角平分线的性质，我们还可以从角平分线定理的角度来求点.根据角平分线定理，可以求出直线l与x的交点坐标，从而求出直线l的方程.

(4)三角形的视角

从三角形的角度来考察本题，由角平分线联想到等腰三角形中三线合一的性质，此题也迎刃而解.

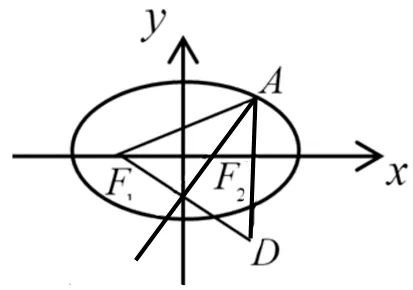
图2

构建等腰三角形，如图2，延长AF2至AD使AD=AF1=5，则知点D(2,-2)，由等腰三角线三线合一知F1D的中点M(0,-1)在直线l上，进而求出直线方程.解决问题的过程中用联系的观点看问题，这是数学思维必备能力之一.

(二)求斜率

(1)向量的视角

(2)三角函数的视角

(3)椭圆切线的视角

本题以椭圆为背景，而椭圆的几何光学性质等也为解题提供了不一样的视角.

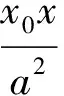
四、反思总结，融会贯通

反思是一种积极的探究行为，通过反思，有利于提高发现问题的能力，有利于完善解题过程，增强自我调控意识.反思解题的过程，运用的数学知识和数学思想方法，反思解题策略，在反思的过程中，加深对问题本质的理解，提炼对数学问题的认识.本题是一道基础题，学生很容易想到第一种求点的方法，如果问题到这一步就结束，可以说是轻描淡写的收场，那么师生就会错过多视角多方位的对这个问题的理解和探究.求点的坐标，那么求哪些点的坐标呢？有哪些不同的方法呢？如果在平时的解题中不仅仅满足于把问题解决了，而是习惯性地追问自己：还有不一样的方法吗？还有更好的方法吗？如果经常这样追问自己，解题的方法和思路就会越来越宽，解题能力也会不断提高.本题是典型的求直线方程问题，除了求点，很自然就会想到，求斜率行不行呢？怎么去求斜率呢？这样思路就打开了.问题与问题之间不是孤立的，许多表面上看似无关的问题却有着內在的联系，解题不能就题论题，要寻找问题与问题之间本质的联系，要质疑为什么有这样的问题？他和哪些问题有联系？能否受这个问题的启发.将一些重要的数学思想、数学方法进行有效的整合，创造性地设问，在不断的知识联系和知识整合中，丰富认知结构中的内容，体验“创造”带来的乐趣.

在平时的解题教学中，要有意识的引导学生进行解题回顾和总结，完善解题认知结构.在解题后，引导学生对解题中用到的数学知识点，数学思想方法和解题技巧进行回顾，对典型的问题进行深入地挖掘、研究、引申和推广，使学生在回顾反思的过程中亲身体验，总结和积累数学解题经验，从而提升学生的数学解题能力和数学思维能力.