从2017年全国高考题看公式法求空间角的意义

重庆市荣昌区大成中学 (402460)

熊福州

从2017年全国高考题看公式法求空间角的意义

重庆市荣昌区大成中学 (402460)

熊福州

图1 图2 图3

公式①,②形式整齐，便于记忆，利用公式①,②就可不构成角计算出立体几何中的所有角其中，公式①解决二射线(包括异面射线)角和二面角计算，公式②专解决线面角计算，当θ1,θ2,θ3,α3有特殊角时，用公式①,②就更简捷，当θ1,θ2,θ3,α3有直角时尤为简捷，使用时根据公式①,②特别注意首先确定计算好θ3(去二面角棱射线后的另两射线角)，再依次计算出θ1，θ2(二面角棱射线与另两射线角).

图1中把AB平移到虚线A1B1(图2),则θ3就是异面射线A1B1与AC所成的角，异面直线A1B1与AC的夹角余弦值为|cosθ3|=|cosθ1cosθ2+sinθ1sinθ2cosα3|.又如图3，分别在二面角α-MN-β的两个半平面内的二射线AB,DC,只要知道∠BAD=θ1，∠CDN=θ2(AD为射线方向)，二面角α-MN-β=α3，就可由①计算出二射线AB,DC所成角的余弦值，这就是说，空间二射线角的计算，除了用正、余弦定理解三角形外，都可用公式①直接计算，只是必须首先明确二射线分别在哪个已知二面角的两个半平面内，再确定二射线与二面角棱射线的角.

例1 (2017年全国高考卷Ⅱ理10)如图4，已知直三棱柱ABC-A1B1C1中，∠ABC=120°，AB=2,BC=CC1=1为,则异面直线AB1与BC1所成角的余弦值为( ).

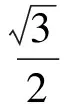
图4

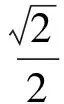
例2 (2017年全国高考卷Ⅲ理16)a,b为空间两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a,b都垂直，斜边AB以AC为旋转轴旋转，有下列结论:①当直线AB与a成60°时,AB与b成30°；②当直线AB与a成60°时,AB与b成60°；③直线AB与a成的最小角为45°；④直线AB与a成的最大角为60°.其中正确的是________(填写所有正确结论的编号).

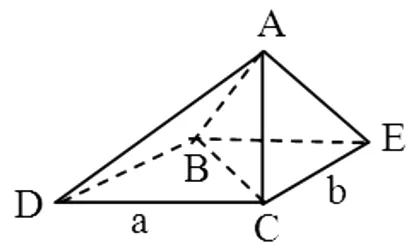
图5

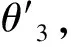
例3 (2017年全国高考卷Ⅲ理19)如图6,四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD,AB=BD.

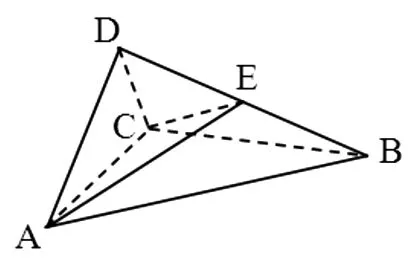
图6

(1)证明：平面ACD⊥平面ABC；(2)过AC的平面交BD于E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D-AE-C的余弦值.

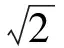
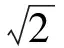
图7

例4 (2017年全国高考卷Ⅰ理18)如图7，在四棱锥P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°.证明：平面PAB⊥平面PAD；(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.

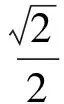
总之，空间角都有三个通法，传统几何法(好做不好想)，坐标向量法(好想不好做)，公式法(熟悉了，既好想又好做).

[1]熊福州.一个教科书结论的推广及其应用[J].河北理科教学研究，2011,4.