基于K-最短路径的大规模函数调用关系分析

张晶晶 石剑君 高玉金 计卫星

(北京理工大学计算机学院 北京 100081)

基于K-最短路径的大规模函数调用关系分析

张晶晶 石剑君 高玉金 计卫星

(北京理工大学计算机学院 北京 100081)

函数调用关系反映了软件系统中函数之间的依赖关系，在软件分析、软件测试与软件维护等众多软件工程领域都有着广泛的应用。但在大型复杂软件中搜索两个函数之间的调用关系时 ，由于函数数量众多、函数之间调用关系复杂，使得搜索所需时间较长。为了获得任意两个函数之间的调用路径，提出使用K-最短路径算法，并对K-最短路径算法进行并行化优化，减少搜索时间，为用户分析函数调用关系提供方便。通过对Linux内核3.19(包含40多万个函数结点和110多万调用关系)进行分析，实验结果表明通过并行化优化，并行加速比一般可达5～6倍。

函数调用关系 K-最短路径 路径搜索 Linux内核

0 引 言

随着软件技术的快速发展，软件应用遍及各行各业，人们对于软件各项功能的要求也越来越高，随之而来的是软件代码规模日益增大,代码量达到了百万行乃至数千万行。例如，最流行的开源操作系统Linux 内核的代码量已经从1万多行代码增长到2 000多万行。对于大型软件系统而言，由于代码规模庞大、自身逻辑复杂、说明文档匮乏等特点，使得代码分析工作越来越困难。

函数调用关系一般以一种有向图的形式表示，是程序理解、程序分析中重要的研究内容。在程序理解中，一个函数一般代表一个具体功能或者问题求解的实现，函数调用关系反映了软件系统中函数间的依赖关系。大型程序一般都是通过对函数的组织和调用来实现整个程序的功能要求，掌握函数之间的调用关系对理解程序是非常有帮助的。

除此之外，在软件工程的其他领域函数调用关系也有着广泛的应用，例如集成测试、回归测试[3]、逆向工程、编译优化、软件测试与维护等。在编译优化技术中，一方面通过分析程序的调用关系，使得没有调用链关联的函数的局部变量共享全局存储单元，降低程序运行时对内存的需求，并提高相应存储单元的利用率[1]；另一方面也可以根据建立的函数调用关系，分析函数调用关系中每个函数的寄存器使用集合，估算出每个函数调用点进行上下文保存所需要的最小访存集合，从而减少函数调用点所保存的上下文，消除冗余访存操作，同时也能提升性能[2]。在路径集成测试[4]中，对于大型程序进行完全路径测试几乎是不可能完成的，所以如果将路径测试级别上升到函数组件的级别，根据函数调用关系再结合判断循环分支结构生成组件的控制流图，然后再结合路径测试方法，最后构造出组件继承测试模型，这样可以大大减少测试的复杂度。

考虑到函数调用关系在各个方面的广泛应用，如何能够准确地获取反应实际程序执行时两个函数之间真正的调用关系，一直是大家关注的热点。对于大规模项目而言，查询两个函数之间的全部调用路径可以通过连接查询，但是时间复杂度却很高。因此，出于对性能的考虑，查询两个函数之间的所有调用路径几乎是不可能的。本文提出基于K-最短路径算法查找两个函数之间的调用路径的方法，首先解析源码存储所有函数之间的调用关系，然后通过Yen算法来获得函数之间前K条调用路径，最后再得到函数之间调用关系。K-最短路径问题是典型的NP[23]问题[10]，复杂度高，通过对Yen算法并行化优化，降低了时间复杂度，提高了搜索性能。

1 相关工作

目前，国内外关于静态分析函数调用关系的工具很多。文献[5]中提到三种函数调用关系静态分析方法，分别是使用正则表达式提取、使用开源软件ctags[24]和cscope[25]提取、构建抽象语法树获取函数调用关系。使用正则表达式提取调用关系是最简单的办法，通过扫描每一个源码文件，匹配源码中所有函数定义、存储函数名、参数列表、所在文件等信息。然后再对源码进行第二次扫描，进行匹配函数中调用的函数，再将函数调用关系存储起来。Ctags是一个开源的工具，可以从源程序代码树产生索引文件，通过解析索引文件产生函数之间的依赖关系。Cscope是一个C语言的浏览工具，可以找到函数或者变量定义位置、被调用函数位置等信息。通过Yacc和Lex实现C构建抽象语法树来提取函数调用关系。

文献[6] 提出一个基于RTL的函数调用图生成工具CG-RTL，其核心模块数据预处理是从编译中间结果中提取函数定义以及静态函数调用关系等信息。在CG-RTL的基础上[7]提出了基于内核跟踪的动态函数调用图生成工具DCG-RTL，使用S2E作为获取动态函数调用数据的工具，记录运行时的函数调用和返回信息，分析跟踪信息得到动态和静态函数调用关系。

基于数据库的在线函数调用图工具DBCG-RTL[8]采用动态静态结合的方式从编译过程中提取函数定义、函数间调用信息，以及模块与函数间的调用关系，然后存入数据库。

K-最短路径问题是最短路径问题的另外一种形式，可以最大程度地满足用户对不同路径的需求。K-最短路径问题在其他领域中也有广泛的应用[19]，如路径规划、物流规划、GPS导航、生物医学、社交网络、基于位置的服务(LBS)等。文献[22]中提出通过K-最短路径求不含环路的所有负荷供电路径来计算负荷停电概率和停电风险值。

但在实际应用中所需处理的数据规模很大，使得算法非常复杂，因此，求解算法的选择是解决问题的关键。文献[10]中提出K-最短路径问题分为一般K-最短路径问题和限定无环K-最短路径问题，并阐述了两类问题的求解算法。

2 基于K-最短路径函数调用关系分析与可视化

2.1 K-最短路径算法

随着软件代码规模的日益增大，函数调用关系也越来越复杂，某两个函数之间的调用关系也不止一条。在大规模软件代码中比如Linux 内核，其代码量现在已经增长到2 000多万行。Linux内核3.19的源码中有约40 000多个源文件，源码解析结果中有约40多万个函数结点，110多万条函数调用关系。毫无疑问，Linux内核是一个复杂的系统，获取两个函数之间的调用关系路径也就更加困难。

在分析函数调用关系时，理论上有必要对所有的可达路径进行分析，通过连接查询可以得到函数之间的调用关系。但是搜索两个结点的所有函数调用关系问题是一个NP问题[23]，如果对所有的函数之间的可达路径都进行分析，不仅搜索花费的时间很长，而且在很多应用中并无必要。因此，出于对性能的考虑，可以选择只获取两个函数之间的K条渐次短函数调用路径。

K-最短路径算法是最短路径问题的推广，该算法能得到两个结点之间的K条渐次短路径[9]。在许多领域用户除了希望得到最短路径以外，还希望得到K条渐次短路径。自1971年以来，有大量的文献对K条次短路径进行了研究和探索，本文使用Yen路径算法[9]对Linux内核的函数调用关系进行了分析，并且通过设置不同的K值来测试路径搜索时间，确定最优的K值。

基于函数调用的K条渐次短路径搜索方法的实现主要包括两部分：第一部分是通过初始化建立一个可以表达函数之间调用关系的有向图，第二部分再用K-最短路径算法获取两个函数之间的前K条渐次短调用关系路径。

构建有向图之后调用Yen算法，获得K条渐次短路径。Yen算法采用递推法中偏离路径算法思想，适用于非负权边的有向图结构[10]。假定通过初始化建立有向图G，s和t是图G的两个结点，用P表示从s到t的路径，Pj(j≤K)表示第j条次短路径。其算法的核心思想是利用已求得的前K-1条渐次短路径P1，P2，…，Pk-1来求第K条最短路径，最短路径可以用标准求解最短路径算法得到，比如Dijkstr算法。

Yen算法的伪代码如下：

Input：G(V，E)：weighteddirectedgraph，withsetof verticesVandsetofdirectededgesE； s：thesourcenode； t：thedestinationnode；K：thenumberofshortestpathstofind；1 A[0]←Dijkstr(G，s，t)；2 B←[]；3 fork=1toK：4 fori=0tosize(A[k？1])-2：5 vNode←A[k-1]．node(i)；6 rootPath←A[k-1]．nodes(0，i)；7 foreachpathp∈A：8 ifrootPath==p．nodes(0，i)：9 G．remove(p．edge(i，i+1))；10 foreachnode∈rootPathexceptvNode：11 G．remove(rootPathNode)；12 spurPath←Dijkstra(G，vNode，t)；13 totalPath←rootPath+spurPath；14 B．append(totalPath)；15 A[k]←B[0]；16 returnA；

算法的主要过程是将路径Pk-1中除了终止结点t之外的其他结点作为偏离结点v，计算每个偏离结点v到终止结点t的最短路径；然后再与Pk-1中起始结点s到偏离结点v的路径拼接，构造成候选路径；最后在所有候选路径中选择一条最短路径即为Pk。其中，B是一个Treeset 集合，每次添加路径都会根据路径的权重值排序，使得路径根据权重值按升序排列。

在Linux内核3.19中，搜索函数metronomefb_probe与mac_address_string之间的调用路径，通过统计得到不同K值时所需时间如图1所示。

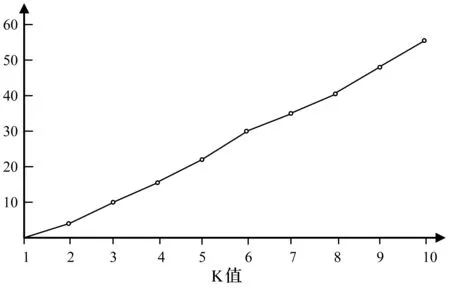
图1 不同K值下搜索两个函数间的路径关系所需时间

实验中机器配置如下：64位windows7操作系统， 4.00 GHz的Intel(R) Core(TM) i7-4790K处理器，8 GB内存。由图1可以看出K值为10时，所需搜索时间将近达到70秒，搜索性能比较差，并行化是一个降低时间复杂度的好方法，因此，本文对Yen算法进行了并行化优化。

获得两个结点间的第K条最短路径主要是将第K-1条路径上除了终止结点之外的每个结点作为偏离结点，再计算偏离结点到终止结点之间的最短路径。即将Pk-1中除了终止结点t之外的任何结点作为偏离结点v，计算每个偏离结点v到终止结点t的最短路径。根据分析，在求解第K条最短路径的过程中，每次求解偏离结点到终止结点的过程是两个相对独立的过程。因此本文使用多线程并行计算一条路径中的每个偏离结点到终止结点间的最短路径，这样可以充分利用多核CPU的并行优势，提高搜索性能。并行优化后的Yen算法的伪代码：

Input：G(V，E)：weighteddirectedgraph，withsetof verticesVandsetofdirectededgesE； s：thesourcenode； t：thedestinationnode； K：thenumberofshortestpathstofind；1 A[0]←Dijkstr(G，s，t)；2 B←[]；3 fork=1toK：4 fori=0tosize(A[k-1])-2：5 pool．execute(YenCandidatesPath(A，i，k，t，G，B))；6 ifalltaskshavecompleted：7 A[k]←B[0]；8 returnA；YenCandidatesPath(A，i，k，t，G，B)：1 graph=G．clone()；2 vNode←A[k-1]．node(i)；3 rootPath←A[k-1]．nodes(0，i)；4 foreachpathp∈A：5 ifrootPath==p．nodes(0，i)：6 graph．remove(p．edge(i，i+1))；7 foreachnode∈rootPath：8 ifnode！=vNode：9 graph．remove(rootPathNode)；10 spurPath←Dijkstra(graph，vNode，t)；11 totalPath←rootPath+spurPath；12 synchronized(obj)：13 B．append(totalPath)；

算法主要思想基本是将第K-1条路径上每个偏离结点提交一个任务(伪代码中第4～5行)，计算其到终止结点的最短路径。等到所有任务执行完毕，再从当前所有候选路径中选择一条最短的路径，即为第K条最短路径。

计算每个偏离结点到终止结点的过程中主要的数据共享有：A、B、t、G。A：此表用于存储前K-1条渐次短路径。B：用于存储候选路径的列表。t：终止结点。G：可以表示函数之间调用关系的有向图，由于每次计算都需要没有删除过任何边的图G，所以在并行化中每次计算之前要将图G做深度复制。

2.2 函数调用关系分析及可视化

对于大型复杂软件，通过传统的文本阅读来理解复杂的函数调用关系比较困难，而可视化工具在代码分析的基础之上，形成了对代码的部分抽象表示，可以加速程序员对代码的理解。我们已经实现一个内核的可视化工具——KernelGraph，KerneGraph参照在线地图服务，是利用可视化技术实现的一个大规模代码理解工具。KernelGraph既可以从全局显示模块之间的关系，以及已有模块中含有bug的百分比，也可以进行函数、变量搜索，函数调用路径搜索等。函数调用路径搜索是KernelGraph的一个重要功能。

Echarts[11]中力导图可以清晰的显示各个结点之间的关系，KernelGraph利用力导图这一特点显示函数和函数之间的调用关系,如图2所示。

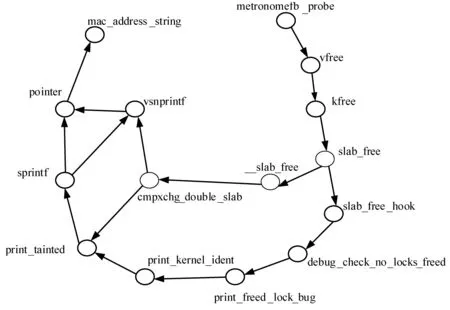
图2 函数之间的路径搜索结果及其可视化表示

图2显示了函数metronomefb_probe与mac_address_string之间的函数调用路径的搜索结果，图中清晰地表达了函数之间的调用关系。

3 实验结果分析

在获取函数调用关系的过程中，首先我们使用 Doxygen[12]来解析Linux内核3.19[13]的源码。Doxygen可以在内核代码的预处理过程中，从每个源文件中提取代码结构并输出一个XML文件。这些XML是源码的结构化数据，包含函数之间的调用关系。然后通过提取XML中关于源码的函数，以及函数之间的调用关系，得到可以表达函数之间调用关系的link文件。

解析Linux内核3.19得到的 link文件中有40多万个结点，110多万条边，结点表示函数，边表示两个函数之间的调用关系。获取两个函数之间的前K条渐次短路径，需要设定一个合理的K值。本文针对函数结点metronomefb_probe与mac_address_string之间的调用关系，统计在设定不同的K值下搜索所需的时间，实验结果如图3所示。

图3 不同K值路径搜索所需时间

通过实验数据表明，在串行算法和并行算法中搜索时间与K值都是成线性比例关系。K值过大，需要搜索时间过长，影响用户体验，K值过小，又无法得到用户所需的调用路径。因此设定一个合理的K值显得尤为重要。

为了获得一个合理的K值，首先解析了Linux内核源码中的Kernel文件夹，得到一个可以表示Kernel文件夹中函数之间调用关系的link文件，文件中包含5 850个结点，10 940个边。再通过分析5 850个结点中每个结点与其他结点之间的调用关系，最后统计出在Kernel文件夹中所有调用路径条数的可能值，如图4所示。

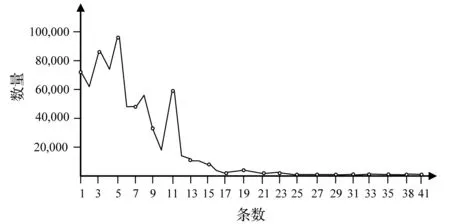
图4 Kernel文件夹中两个函数之间调用关系的路径条数的数量

由图4可以得到，在Kernel文件夹中，函数之间的调用路径条数分别为6和12时，数量值急速下降。因此，在设置K值，一般推荐值为6或者12，或者选择相近值作为查找路径的上限。

通过对Yen算法并行优化之后，搜索所需时间显著降低。通过对Linux内核3.19进行实验统计，分别设置K值为1～10，搜索函数结点metronomefb_probe与mac_address_string之间的路径，得出实验数据如图5所示。

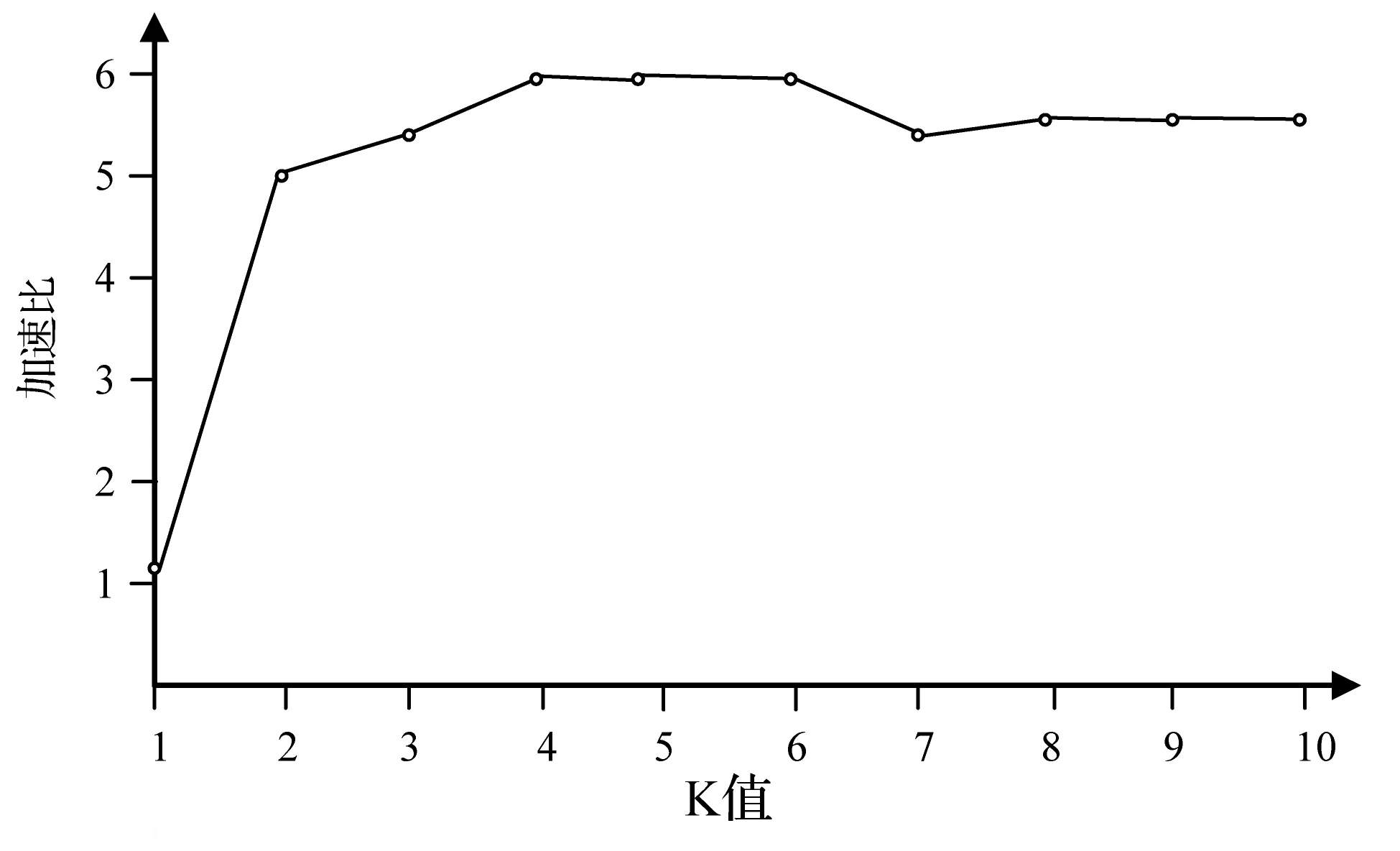
图5 获取前K条渐次短路径并行算法加速比

由于K值为1时，直接调用Dijkstr算法获得最短路径，所以不论算法优化之前还是优化之后，搜索所需时间一样。

4 结 语

随着软件技术的发展，软件代码规模日益增大,函数调用关系也越来越复杂。为保证用户可以获得大型复杂系统中两个函数之间的调用关系，本文使用并行化优化后的K-最短路径算法，对函数调用关系进行分析，并且将函数调用关系用Echarts中的力导图做可视化展示，使得用户可以得到两个函数之间前K条渐次短路径的简洁直观图。当然，目前的工作还有一些需要改进的部分，比如源码解析中，Doxygen不能完全解析出所有函数调用关系。主要是由于大量的预处理指令没有被Doxygen正确识别和处理，例如宏定义和条件编译。经过分析Linux内核3.19的trace动态运行结果得到大约有9 000多个(已识别的函数调用关系有110多万)函数调用关系丢失。在将来工作中，我们将使用特殊的预处理程序和工业级的编译器配合完成源代码的解析，获取在不同预处理条件下函数之间的关系。

[1] 蒋湘涛，胡志刚，贺建飚. 基于调用链分析的低功耗编译优化[J]. 吉林大学学报(工)，2009，39(1)：145-149.

[2] 时磊，王红梅. 基于调用链分析的访存优化技术[J]. 微电子学与计算机，2012，29(7)：32-34.

[3] 郑锦勤，牟永敏. 基于函数调用路径的回归测试用例选择排序方法研究[J].计算机应用研究，2016，33(7)：2063-2067.

[4] 冯国尧. 基于函数调用的路径集成测试模型研究[J]. 电子世界,2015(20):19-20.

[5] 江梦涛，荆琦. C语言静态代码分析中的调用关系提取方法[J]. 计算机科学，2014，41(S1)：442-444.

[6] 孙卫真，杜香燕，向勇，等. 基于RTL的函数调用图生成工具CG·RTL[J]. 小型微型计算机系统，2014，35(3)：555-559.

[7] 向勇，汤卫东，杜香燕，等. 基于内核跟踪的动态函数调用图生成方法[J].计算机应用研究， 2015， 32(4)：1095-1099.

[8] 贾狄，向勇，孙卫真，等. 基于数据库的在线函数调用图工具[J].小型微型计算机系统, 2016, 37(3):422-427.

[9] Hershberger J, Maxel M, Suri S. Finding the k Shortest Simple Paths: A New Algorithm and its Implementaton[J]. ACM, 2007， 3(4)：45.

[10] 徐涛，丁晓璐，李建伏. K最短路径算法综述[J]. 计算机工程与设计，2013，34(11)：3900-3906.

[11] Echarts[DB/OL].2016. http://echarts.baidu.com.cn/.

[12] Doxygen[DB/OL].2016. http://www.doxygen.org/.

[13] Linux kernel archives[DB/OL].2016. https://www.kernel.org/.

[14] The interactive map linux kernel[DB/OL].April 2016. http://www.makelinux.com/kernel_map/intro.

[15] 张素智，张琳，曲旭凯．基于最短路径的加权属性图聚类算法研究[J]．计算机应用与软件，2016，33(11)：212-214,281.

[16] 丁德武. Linux内核函数调用关系的复杂网络分析[J]. 池州学院学报，2012(6)：1-3.

[17] 邱钊. K最短路径算法及其应用研究[D].电子科技大学， 2014.

[18] 于汶雨. K最短路径问题的研究与应用[D].南京邮电大学，2016.

[19] 张钟. 大规模图上的最短路径问题研究[D].中国科学技术大学，2014.

[20] 赵礼峰，于汶雨. 求解k最短路径问题的混合遗传算法[J]. 计算机技术与发展，2016，26(10)：32-35

[21] 苗磊，陈莉君. 基于静态分析的函数调用关系研究[J].计算机与数字工程，2014，42(9)：1653-1656.

[22] 王增平，姚玉海，张首魁，等. 基于k最短路径算法的负荷停电风险在线评估[J]. 电力自动化设备, 2016，36(1)：1-5.

[23] George H Polychronopoulos．Stochastic Shorten Path Problems with Recourse[J]. Networks, 1996, 27(2):133-143.

[24] Ctags[DB/OL],2016. http://ctags.sourceforge.net/.

[25] Cscope[DB/OL].2016.http://cscope.sourceforge.net/.

ANALYSYSOFLARGE-SCALEFUNCTIONCALLRELATIONBASEDONK-SHORTESTPATH

Zhang Jingjing Shi Jianjun Gao Yujin Ji Weixing

(SchoolofComputerScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China)

The function call relationship reflects the dependency between the functions in software system, and has been widely used in much software engineering fields, such as software analysis, software testing and software maintenance. However, in large complex software search between the two functions of the call relationship, due to the large number of functions, calls between the complex relationships, making the search takes longer. In order to obtain the calling path between any two functions, we proposed to use K-shortest path algorithm and optimize the K-shortest path algorithm to reduce the search time, which was convenient for users to analyze the function call relationship. Through the analysis of Linux kernel 3.19 (including more than 400,000 function nodes and 110 million call relationships), the experimental results showed that through the parallel optimization, parallel speed was 5～6 times than the average.

Function call relationship K-shortest Path search Linux kernel

2017-03-05。张晶晶，硕士生，主研领域：代码分析可视化。石剑君,博士生。高玉金,讲师。计卫星,副教授。

TP3

A

10.3969/j.issn.1000-386x.2017.12.005