一种基于Rabin和Paillier的数字签名方案

魏文燕 彭维平 李子臣 汤永利

1(河南理工大学计算机科学与技术学院 河南 焦作 454000) 2(北京印刷学院信息工程学院 北京 102600)

一种基于Rabin和Paillier的数字签名方案

魏文燕1彭维平1李子臣2汤永利1

1(河南理工大学计算机科学与技术学院 河南 焦作 454000)2(北京印刷学院信息工程学院 北京 102600)

从单向陷门函数的角度分析Paillier签名方案的安全性，针对当前Paillier签名方案中效率和安全性不能兼顾的现状，提出一种基于Rabin和Paillier的数字签名方案。方案以改进的Paillier签名方案为基础，结合Rabin体制中的Blum-Williams单向函数，以及签名过程中s1的计算困难性基于模合数的平方根问题，并对提出的方案进行了安全性分析和效率分析。分析结果表明，新方案有效解决了现有Paillier签名方案中存在的问题，在保证签名安全性的同时具有较高的效率，在现实生活中更具实用性。

数字签名 Paillier密码体制 单向陷门置换 二次剩余 安全性

0 引 言

数字签名是密码学中的一项基本原语。1976年，Diffie等[1]首次提出用陷门单向函数实现公钥密码体制和数字签名的思想。1999年，Paillier[2]在欧密会上提出了基于判定合数剩余困难问题的Paillier单向陷门函数，并以此为基础构造出了Paillier公钥密码体制和数字签名方案。之后，国外研究学者对其进行了广泛的研究，并陆续提出了一系列的改进方案[3-6]。国内姜正涛等[7-8]通过选取特殊的参数改进了Paillier体制，提高了加密体制的效率。由于Paillier体制提供了一种新的密码算法设计思路，并且Paillier单向陷门置换通过一定方式转化可以很好地用于加密、签名及认证，不少研究人员对基于Paillier的数字签名方案的构造进行了研究。其中，Man等[9]基于Paillier单向陷门函数构造了基于身份的加密和签名方案，弥补了相关研究的空白。Zhou等[10]应用Paillier的部分单向陷门函数提出了一种基于成员身份的群签名方案，可抵抗群管理员陷害攻击。Wang[11]提出了适用于低端计算设备的基于Paillier签名的服务器辅助验证签名方案，有效地降低了验证者的计算复杂度。Cheng等[12]利用Paillier签名方案的同态性构造了同态签名方案，能防止线性网络编码系统遭受污染攻击。岳泽轮等[13]提出了一个高效安全的基于Paillier密码体制的签密方案，同时实现了保密和认证功能。Ting等[14]首次提出了基于Paillier的门限代理签名方案，并证明了该方案在选择消息攻击和选择证书攻击下具有不可伪造性。目前，基于合数剩余类问题的签名方案仍有待研究，但是Paillier体制陷门计算开销较大，在一定程度上会影响签名方案实际应用中的效率。郑晖等[16]借鉴姜正涛等人的思路[7]改进了Paillier体制的单向陷门置换，对Paillier数字签名进行了改进，提高了签名产生和验证的效率。Cao等[15]对Paillier体制进行了深入研究，并指出利用Paillier陷门单向函数易直接构造出安全的数字签名方案，但是Paillier陷门函数的众多变体失去了这个特性。

本文通过对Paillier签名方案进行研究，针对现有方案的不足之处，提出了一种改进的基于Paillier和Rabin的数字签名方案。该方案以Paillier体制为基础，结合二次剩余理论，在满足正确性、安全性的基础上，同时具有较高的效率，在现实生活中更具实用性。

1 预备知识

1.1 相关定义与定理

定义2在RSA加密体制中，模为n(n=pq，p和q为两个大素数)，加密指数为n时，即z=ynmodn，当n的分解未知时，已知z和n求y的问题是难解的，记作RSA[n,n]。

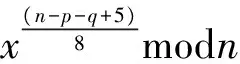
定理3[2]Class[n,1+n]⟸RSA[n,n]⟸Fact[n]。

1.2 Blum-Williams函数

1979年，Michael Rabin提出了一种基于二次剩余理论的可证明安全的密码体制，简称Rabin密码体制。由于Rabin体制并不是以一一对应的单向陷门函数为基础，因此可能有两个以上的明文对应同一密文。为了避免上述缺陷及提高解密的速度，Williams采用Blum素数对其进行了改进，即选取相同长度的不同素数p和q，满足p≡q≡3mod4，n=pq为Blum整数，并且利用Jacobi运算将Rabin函数限定在Qn上。Blum-Williams方案中函数G的定义如下，以下简称Blum-Williams函数[17]。

G:Qn→Qn

G(x)=x2modn

Blum-Williams函数是一个单向陷门置换，其单向性与分解Blum数等价，且若已知n的分解，x可被唯一求解。文献[18]利用Blum-Williams函数的思想构造了一种Rabin签名方案，解决了签名消息空间受限的问题。由于Rabin方案在验证签名时具有很高的效率，因此在签名方案的构造方面得到了广泛应用[17-18]。

2 对Paillier签名方案的研究

2.1 Paillier体制

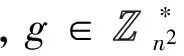
εg(m,r)=gm·rnmodn2

Paillier证明了εg是一个单向陷门置换，其单向性基于合数幂剩余类计算问题是困难的，然后构造了一种在适应性选择消息攻击下，具有不可伪造性的数字签名方案[2]。

Paillier体制的主要缺点是陷门计算的开销较大，加密解密的开销本质上都需要模幂运算，数字签名亦如此。为了提高加解密的速度，文献[2]建议g取2，但是后续研究发现选取g=1+n更为合理[3]。选取g=1+n时，g的阶为n，且对于任意的m，等式(1+n)mmodn2=(1+mn)modn2成立。基于上述研究成果，姜正涛等人选取特殊参数g=1+n研究了Paillier变体的加密函数F，改进了Paillier加密体制，函数F的定义如下：

F(m,r)=(1+mn)rnmodn2

2.2 文献[16]方案回顾

文献[16]根据文献[7]中基于函数F的加解密思路，改进了Paillier单向陷门置换，并将其应用得到改进后的Paillier数字签名方案[16]如下，提高了Paillier签名的产生和验证效率。该方案主要由密钥生成、签名生成和签名验证三个部分组成。

因此，签名者的公钥为n，私钥为(p,q)或者λ。

2) 签名生成 对于给定的消息m，先计算h(m)，然后利用私钥得到对应签名(s1,s2)如下。

s1=bL(h(m))modn

3) 签名验证 签名接收者收到消息m和数字签名(s1,s2)，可通过验证下列等式是否成立。若等式成立，则接受该签名，否则拒绝。

2.3 Paillier签名方案的安全性分析

由于Paillier签名方案[2]和文献[16]改进的签名方案都是应用Paillier单向陷门置换得到的，因此，以下从Paillier单向陷门置换加密的角度，分析了Paillier签名方案的安全性。

文献[2]利用函数εg构造了Paillier单向陷门置换方案，已知密文c=gm·rnmodn2，求解m为计算合数剩余类难题，即Class[n]，在已知n的分解的前提下才可以解决。而且由于函数εg是双射，已知c和m，可以进一步求解RSA[n,n]问题得到唯一的r，上述性质使得Paillier加密方案可直接转化为安全的数字签名方案。

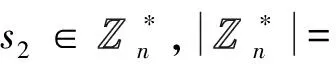
1) 攻击1 给定消息m′，已知签名算法的公钥n和签名验证函数，攻击者能以不可忽略的概率伪造出对应的有效签名σ=(t1,t2)，具体操作如下。

(1) 由消息m′和Hash函数h，可得到h(m′)。

(3) 根据扩展欧几里德算法可求出r-1modn2的值。

(4) 由下式计算得到t1的值，即：

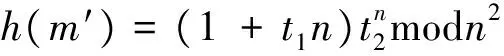
综上所述，文献[16]应用文献[8]中思路改进的Paillier签名方案，虽然提高了签名产生的效率，但是同时也破坏了s1的计算基于求解离散对数问题这一特性，使得该方案不能有效抵抗攻击1，其安全性有待进一步改进。

3 新的签名方案

通过对Paillier体制及其变体的深入研究，在改进的Paillier签名方案[16]的基础上，引入二次剩余问题对其安全性进行改进，即基于Blum-Williams函数构造了一个新的数字签名方案。新方案弥补了现有Paillier签名方案的不足，解决了签名方案安全性和效率之间的矛盾，方案具体如下。

1) 密钥生成 选取两个不同的大素数p和q，其中p≡3mod8，q≡7mod8，p和q大小相近，λ=lcm(p-1,q-1)，且n=pq，c=λ-1modn，L函数的定义和Hash函数h的选取如文献[16]签名方案中所述。签名方案的私钥为(p,q)，公钥为n。

2) 签名生成 给定一个消息m，签名者可按如下步骤对其进行签名。

Step1由m可得到相应的h(m)，并计算：

s=cL(h(m))modn

(1)

Step2首先验证式(1)中得到的s是否满足(s,n)=1，如果不满足，则通过引入一些随机数来修改s的值，使得(s,n)=1成立。事实上，由文献[18]可知，当n很大时，(s,n)不为1的概率其实可以忽略不计。上述步骤完成之后，计算a如公式：

(2)

Step3由Jacobi相关运算可知，(2-as)modn∈Jn，这时，b的计算如公式：

(3)

s1=(2-as)dmodn

(4)

Step5计算：

(5)

则消息m对应的签名为σ=(s1,s2,a,b)，将消息及其对应的签名一起发送给签名接收者。

3) 签名验证 签名接收者收到消息m及其签名σ后，验证下列等式是否成立，若等式成立，则接受签名，否则，拒绝该签名。

(6)

4 方案分析

4.1 正确性分析

由签名过程可得下式：

式中：2-as∈Jn，n=pq，其中p和q满足p≡q≡3mod4，因此：

(1) 当2-as∈Qn时，b=0，由定理2可知：

(2-as)2d=(-1)b2-asmodn

(2-as)2d=-2-as=(-1)b2-asmodn

因此，下列等式成立，即：

-1)bn=(1+sn)modn2

4.2 安全性分析

由于文献[16]中签名方案的安全性基于RSA[n,n]问题的难解性，而本文方案为了弥补文献[16]中方案的安全缺陷，在原方案的基础上引入了二次剩余理论，使得s1的计算依赖于大整数分解难题。事实上，本文的方案是融合Rabin签名方案和改进后的Paillier签名方案之后形成的，由于两者的结合很好地克服了原有方案的安全缺陷，因此本文方案具有更高的安全性。而由定理3可知，RSA[n,n]可以归约到Fact[n]上，即求解RSA[n,n]不会比大整数的素因子分解问题更难，而Rabin签名方案的安全性已被证明与大整数分解的困难性等价。因此，整体来说，本文提出的数字签名方案的安全性基于大整数分解难题。

引理1若大整数分解问题是困难的，则本文提出的签名方案可抵抗适应性选择消息攻击。

证明假设攻击者向签名方发送对消息m1和m2的签名请求，并且得到了相应的签名分别为σ1和σ2，即σ1=(s1,t1,a1,b1)，σ2=(s2,t2,a2,b2)，则可进行验证得到如下等式，即：

且攻击者可由上述等式得到下式，即：

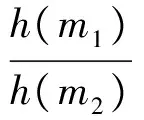
在大整数分解困难的前提下，本文方案能抵抗各种已知的伪造攻击，与文献[16]中方案相比，具有更高的安全性。

4.3 效率分析

从方案的整体设计思路上看，如表1所示。本文方案与文献[2]和文献[16]都是基于公钥加密构造的签名，而文献[19]中签名方案则是构造了一种“等式关系”进行签名。本文方案与文献[2]和文献[16]中签名方案的安全性都基于数论中的困难问题，而文献[19]中方案的安全性基于RSA-Paillier陷门函数为单向陷门置换。

表1 签名方案设计思路的比较

(1) 运算代价的比较 在运算代价上，本文从以下四个方面比较了三种签名方案的效率，如表2所示。1-L表示1个L函数的运算。1-D(n)表示一个模n的除法运算。1-M(n)表示1个模n的乘法运算。1-E(n)表示1个模n的幂运算。在Paillier签名产生过程中，L函数的计算量相对较大。由表2可知，文献[16]中的方案之所以提高了Paillier签名方案的效率，是因为其在L函数运算和模幂运算上的计算量都有所减少。而本文方案在不增加L函数运算的基础上，出于安全性考虑，在文献[16]方案的基础上只增加了一次模幂运算，与安全的Paillier签名方案相比，具有明显的计算优势。相应的，与文献[16]中签名方案相比，在签名验证过程中，本文方案也避免了计算量相对较大的模幂运算，只增加了一次模乘运算，而且在计算上明显优于Paillier签名方案。而文献[19]中的方案由于利用的单向函数和构造方法的特殊性，签名产生阶段不需要L函数的运算，但是签名验证的运算代价与本文方案相同。

表2 签名方案运算代价的比较

(2) 通信代价的比较 由于签名者和签名接收者之间传输的主要是公开参数和产生的签名，因此通信代价考虑的是传输的公开参数的数据量和签名的长度。在表3中， |X1|表示n中元素的长度，|X2|表示中元素的长度，|X3|表示n2中的元素。如表3所示，在公开参数传输的数据量上，本文方案与文献[16]中方案相同，只需要传输公开参数n，不需要传输g，与文献[2]的方案相比，传输参数的数据量降低了，减少了带宽。另外，本文的方案产生的签名的长度仅仅比文献[16]中方案增加了a和b两个比特因子，而且由于签名验证方可以在验证过程中计算出b，所以实际上只增加了一个比特因子，在n比较大时，可以忽略不计，因此两方之间需要传输的签名的长度基本没有变化。由此可知，在通信代价上，本文方案与文献[16]的方案基本相同，相较于Paillier签名方案[2]都有所减少。而文献[19]中签名由三个部分组成，与本文方案相比，签名长度较长，需要传输的数据量也较多。

表3 签名方案通信代价的比较

总体说来，与现有的同类方案相比，本文方案在运算代价和通信代价方面具有较高的效率。

5 结 语

从改进Paillier签名方案的安全性入手，本文先从单向陷门函数的角度分析了Paillier签名方案的安全性，然后通过举证一种伪造攻击方法，指出改进的Paillier签名方案虽然提高了签名生成和验证的效率，但是存在安全缺陷，并结合Rabin体制中的Blum-Williams函数，得到了一种更加完善的数字签名方案，解决了签名方案安全性和效率之间的矛盾。新方案中s1的计算困难性基于模合数的平方根问题，即已知签名中的s2和h(m)，在n的分解未知的前提下，并不能有效地计算出签名部分s1。经分析证明，本文方案在保证签名方案安全性的基础上具有较高的效率。

[1] Diffie W,Hellman M.New directions in cryptography[J].IEEE Transactions on Information Theory,1976,22(6):644-654.

[2] Paillier P.Public-key cryptosystems based on composite degree residuosity classes[C]//International Conference on Theory and Application of Cryptographic Techniques.Springer-Verlag,1999:223-238.

[3] Damgård I,Jurik M.A generalisation,a simplication and some applications of Paillier's probabilistic public-key system[C]//PKC’01 Proceedings of the 4th International Workshop on Practice and Theory in Public Key Cryptography:Public Key Cryptography.Springer-Verlag London,UK,2001:119-136.

[4] Catalano D,Gennaro R,Howgrave-Graham N,et al.Paillier’s cryptosystem revisited[C]//ACM Conference on Computer & Communications Security,2002:206-214.

[5] Galindo D,Martyn S,Morillo P,et al.A Practical Public Key Cryptosystem from Paillier and Rabin Schemes[C]//International Workshop on Theory and Practice in Public Key Cryptography:Public Key Cryptography.Springer-Verlag,1993:279-291.

[6] Bresson E,Catalano D,Pointcheval D.A simple public-key cryptosystem with a double trapdoor decryption mechanism and its applications[J].Lecture Notes in Computer Science,2003,2894:37-54.

[7] 姜正涛,刘建伟,秦波,等.加密|n|+k bit明文的高效公钥概率加密体制[J].北京航空航天大学学报,2008,34(1):43-46.

[8] 姜正涛,刘建伟,王育民.Paillier-Pointcheval公钥概率加密体制的改进[J].计算机工程,2008,34(3):38-39.

[9] Man H A,Wei V K.ID-based Cryptography from Composite Degree Residuosity[J].Iacr Cryptology Eprint Archive,2004,2004.

[10] Zhou Sujing,Lin Dongdai.An interesting member ID-based group signature[J].Recent Developments in Algebra & Related Areas,2007,2007:279-302.

[11] Wang Zhiwei.A new construction of the server-aided verification signature scheme[J].Mathematical and Computer Modelling,2012,55(1-2):97-101.

[12] Cheng Zhen,Chi Kaikai,Tian Xianzhong,et al.Secure network coding based on homomorpuic signature against pollution attacks[C]//2012 IEEE 2nd International Conference on Cloud Computing and Intelligence Systems,Hangzhou,2012:1092-1096.

[13] 岳泽轮,韩益亮,杨晓元.基于Paillier公钥密码体制的签密方案[J].小型微型计算机系统,2013,34(10):2310-2314.

[14] Ting P Y,Hseu C H.A secure threshold Paillier proxy signature scheme[J].Journal of Zhejiang University Science C,2010,11(3):206-213.

[15] Cao Zhengjun,Liu Lihua.The Paillier’s cryptosystem and some variants revisited[J].International Journal of Network Security,2017,19(1):91-98.

[16] 郑晖,徐赐文.一种改进的概率加密体制[J].计算机工程,2010,36(1):149-150.

[17] Elia M,Piva M,Schipani D.The Rabin cryptosystem revisited[J].Applicable Algebra in Engineering Communication & Computing,2011,26(3):251-275.

[18] 邱卫东,陈克非,白英彩.新型Rabin签名方案[J].软件学报,2000,11(10):1333-1337.

[19] Wang Zhiwei.An efficient signature scheme from Catalano’s trapdoor[J].Journal of Electronics (China),2010,27(4):528-530.

ADIGITALSIGNATURESCHEMEBASEDONRABINANDPAILLIERCRYPTOSYSTEM

Wei Wenyan1Peng Weiping1Li Zichen2Tang Yongli1

1(CollegeofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)2(SchoolofInformationEngineering,BeijingInstituteofGraphicCommunication,Beijing102600,China)

After analysing the security of the digital signature schemes of Paillier based on the trapdoor one-way function, we proposed a digital signature scheme which was based on Rabin and Paillier to resolve the problem of efficiency and security in Paillier signature scheme. The scheme was on the basis of the improved Paillier signature scheme which was more efficient than the original scheme, combined with Blum-Williams one-way function in the Rabin system, and the computational intractability of s1 depended on the calculation of square root modulo composite. Then, the security and efficiency of the new scheme were also analysed. The analysis results showed that the new scheme can effectively solve the existing problems in the existing Paillier signature scheme, and it was more effective in ensuring the security of the signature and was more practical in real life.

Digital signature Paillier cryptosystem One-way trapdoor permutation Quadratic residue Security

2017-02-17。国家自然科学基金项目(61370188)；河南省科技厅重大科技攻关项目(132102210123)；河南省教育厅重大科技攻关项目(13A520321，12A520021)；河南理工大学博士基金项目(672515/194)。魏文燕，硕士生，主研领域：密码学。彭维平，副教授。李子臣，教授。汤永利，副教授。

TP309

A

10.3969/j.issn.1000-386x.2017.12.057