突破中学数学“假性理解”的“三维思考”

朱云虎

(江苏省南通市通州区金沙中学 226500)

突破中学数学“假性理解”的“三维思考”

朱云虎

(江苏省南通市通州区金沙中学 226500)

数学的体现形式有三种：文字形态，式子形态，图象形态，这三种形态成为“数学三维”，巧妙的将这三者之间进行转化，就可以构建起学生的数学能力.

文字；式子；图象；数学三维；数学能力

中学数学中“假性理解”是一个比较普遍的现象，在不同的学生层次中均有表现.具体的表现：学生常常发现无法独立读懂题意，解题过程中无法利用题中的条件等等.当教师在解读题目的时候，学生常常又能自我的突破，为什么会出现这种情形？经过多年比较，发现教师的思维方式和学生有很大的区别.教师比较关注于条件的自身分析，而学生却更多地依赖于已有类试题的解题思路.本文就对教师的自身思维分析，来阐述“数学三维”的使用特点，以引导学生的思维生成.

一、三维的特征

1.文字的特殊性

文字是常见的信息的载体，是我们记载信息的一种重要的手段，可以确的表述某种客观事实.它的缺点是“让部分简单的事实描述起来复杂化”，失去了某种简洁性和直观性.

2.式子的特殊性

式子是数学内容表现的主要形式，也是学生解答解答题的主要形式.式子的最大优点是严谨的表现数学的内容，所谓的“0就是0，1就是1”，没有言语误解的可能性.缺点是式子过于抽象化，不易理解.

3.图象的特殊性

图象是体现数量关系和变量关系最好的载体，通过图象我们可以清晰的看出量与量之间变化的过程，用图象来体现数学具有直观、明了.缺点是无法准确的表述两个量之间的定性关系.

4.三维的关系

数学问题的具体体现通过文字的描述、式子的表达、图象的直观来表示数学相关的知识，这三种维度都是数学知识的具体体现.但每个维度都有其优点和缺点，如何通过三者之间的合理转化利用其各自的优点解决问题是我们解决数学问题的关键所在.

二、三维度之间的应用特点

1. 文字与式子之间的转化

例1 已知一次函数f(x)满足f(f(x))=4x+3，则f(x)= .

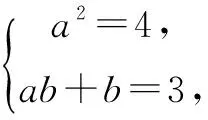
所以f(x)=2x+1或f(x)=-2x-3

评注题中一次函数的具体显现f(x)=ax+b是解决这一问题的关键.

变式已知函数g(x)=x+1，二次函数f(x)满足f(g(x))=x2+3x+3，则f(x)= .

例2 (2015年福建文科)若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在[m，+∞)单调递增，则实数m的最小值等于____．

解析由f(1+x)=f(1-x)得函数f(x)的图象关于x=1对称，由f(x)=2|x-a|可得图象关于x=a对称， 故a=1，则f(x)=2|x-a|.由复合函数单调性得f(x)在[1，+∞)递增，故m≥1，所以实数m的最小值等于1．

评注本题思路的关键在于从函数式子中看出对应函数所要表达的内涵：对称性和单调性.从而使得信息明朗化，利于数学实际问题的解决.

2.文字与图象之间的转化

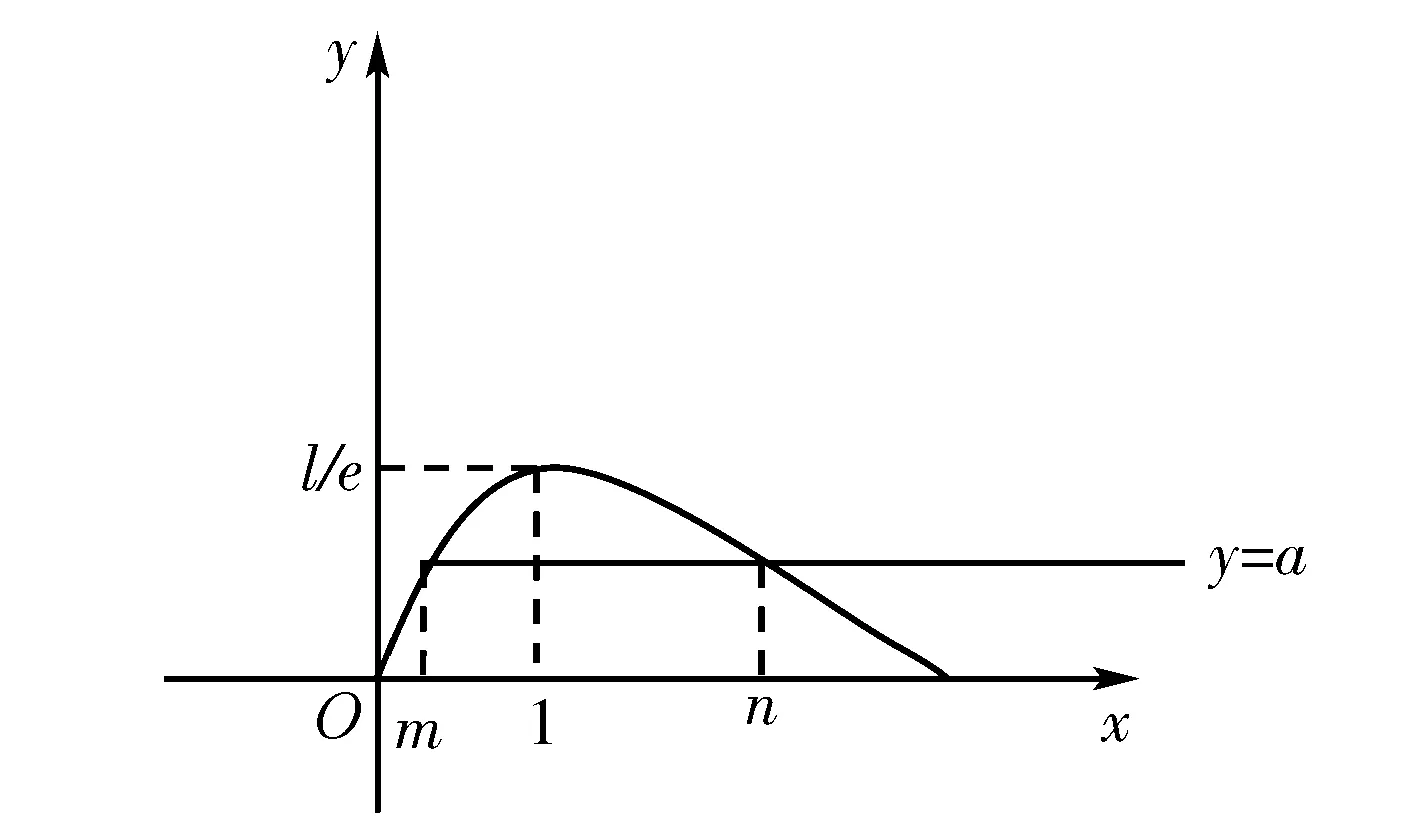
评注本题解决的关键是将题中的大量文字信息变成图象信息，即作出表现意思的图象.

评注本题的关键在于从图形中看出“同时函数图象上的点到对称轴的距离越大则相应的函数值越大”，从而正确的建立起|x1|>|x2|⟺f(x1)>f(x2)，解决问题.

3.式子与图象之间的转化

数学思维活动是一个严密的活动，更是一个开放的活动.它的基础在于学生要求比较好的知识基础，同时也要有丰富的联想.其中的联想其实就是对题中所涉及的知识点进行灵活的转化，特别是三个维度之间的合理转化，通过合理的转化可以更为深刻的认识到知识的本质，认识到知识在具体题中的应用要求，触摸到各个知识点之间的交汇之处，从而生成解题的思路.因此，从某种意义上来说，学生对三维的处理能力代表着学生的解题能力，也代表着学生的思维水平.培养好学生的三维能力，是解决学生“假性理解”的一个重要举措.

[1]单墫，等.普通高中课程标准实验教科书必修1[M].南京：江苏凤凰教育出版社

G632

A

1008-0333(2017)31-0024-02

2017-07-01

朱云虎(1979.1-)，汉，本科，江苏省南通人,中学一级教师，从事中学数学教学研究.

杨惠民]