用构造法巧解不等式问题

母贺楠

(河北省唐山市乐亭县第一中学 063600)

用构造法巧解不等式问题

母贺楠

(河北省唐山市乐亭县第一中学 063600)

在高中三年的学习中，我们学到了许多数学知识.如何将知识转化为能力，成为我们解决问题的工具，针对这一问题，本文仅就不等式问题的求解，谈些认识与体会.

构造法；不等式问题；模型

构造法是对数学知识的开拓性、创造性运用，对发展数学思维，提升数学素养有着重要的作用.本文仅就不等式(最值)的有关问题，说明构造数学模型的若干途径.

一、构造相应函数

点评函数是高中数学知识的主线.根据题目中式子的特征，构造相应的函数模型，利用函数的性质(单调性，奇偶性，最值)解题，是最基本最重要的方法.

二、构造方程

例2 设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值为____.

解令2x+y=k,即y=k-2x，代入已知式，整理得6x2-3kx+k2-1=0.

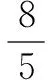
点评根据解题需要构造出相应的方程，是常用方法.构造的途径有利用根的定义，韦达定理，判别式等.

三、构造三角式

点评本题的常规解法是用直线方程与圆的方程联立，求出弦长，再求面积的最大值，十分烦琐.而上述解法恰当引入角变量θ，转化为三角式问题，解法巧妙简捷.

四、构造数列

点评将待证式变形后，逆向思维，观察出分式是等比数列前n项和，通过构造相关数列，使问题简捷获解.

五、构造二项式

例5 求证2n>2n+1(n∈N*且n≥3).

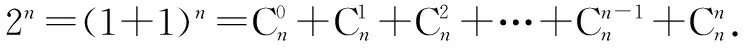
由n≥3知展开式至少有4项，故

点评以上证明不用常规的数学归纳法，而巧构二项式，速证不等式.

六、构造向量

例6 设x、y、z>0，xyz=1,求证

分析将左边各分式看成某式的平方，来构造两个向量的模与数量积，然后利用模与数量积的不等式求解.

构造法解题是以坚实的基础知识为根基的，通过敏锐的观察，广泛的联想来实现的.这需要平时的积累.

[1]张志兵.例谈“构造法”在高中数学解题中的应用[J].数学教学研究，2013(7).

[2]苏亦亚.浅谈“构造法”在高中数学解题中的运用[J].中学数学，2014(6)：62～63.

[3]孙春生.构造法中的奇葩[J].中学生数学，2010(11)：39～41.

G632

A

1008-0333(2017)31-0046-02

2017-07-01

母贺楠，河北省唐山市乐亭县第一中学，高三学生.

杨惠民]