如何研究双变量的最值问题

杨 帆

(江苏省海门中学 226100)

如何研究双变量的最值问题

杨 帆

(江苏省海门中学 226100)

本文就双变量的最值问题，分类举例加以说明，由此归纳出一般的解题原则.

双变量；最值问题；范围

近几年的高考或者大市级的高考模拟卷中都考到双变量的最值或者取值范围问题，而这类问题学生在处理的时候往往比较棘手，短时间内找不到合适的方法，在考试的时候浪费了很多的时间，走了很多弯路.本文主要针对这类问题利用三个主要例题及其相应的变式题目，进行一下探索和方法的总结.有这些方法的思考和意识，希望能为学生思路的打开起到作用.

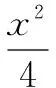
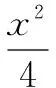
所以令f(t)=-12t2-2t+12,t∈[-1,1]，

评析这道题求目标函数3x2-2y的最值，看似其里面有两个变量的，其实有条件的方程约束，本质上为单变量的最值问题，因此首先想到消元，采用代入消元法.

变题1 条件不变，问题改为：求3x-2y的最值.

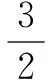
变题2 条件不变，问题改为：求3x2-2xy的最值.

解析在这道题中，目标函数的几何意义显然不容易发现，所以采用三角消元比较合适，但是三角消元也是具有一定的局限性，对条件中关于双变量的方程的结构要求较特殊.

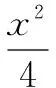
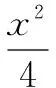
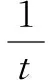
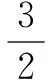
评析这道题目的特点是：目标函数代入消元不好处理，目标函数没有明显的几何意义，条件的形式不好用三角替换.在这种情况下，虽然条件是关于双变量的方程，本质上问题中含有一个变量，但是难点就在于如何将二元化为一元，这时我们常用的技巧就是：能不能将条件中的方程用参数方程表示(观察是否能因式分解)达到消元目的；观察目标函数的结构是否具有某种特点，进行相关配凑，整体换元到达消元目的；将目标函数令为t，反过来表示代入条件方程，转化为方程有解问题(本质上换主元)，将t视作参数，达到研究t的取值范围的目的.

通过以上几个题目我们发现实际上这类在方程约束下的双变量最值问题，本质上难点就在于如何将二元化为一元，我们在解决问题时应该想到以下几种方法：①代入消元；②三角消元；③目标函数的几何意义；④条件方程转化为参数方程；⑤整体换元；⑥令目标函数为t回代条件方程转化为方程有解问题.当然以上几种方法解题时都要注意变量的范围.

刚刚这类问题是方程约束下的双变量最值问题，其实还有一类题目虽然双变量在条件中有方程的约束，但不是求某个目标函数的取值范围，而是个固定的值.这类双变量问题中，不能用以上几个方法，我们该如何思考，下面我来看一道题.

法二：在法一中得到了：s+t-2=ln(st)即s+t-2=lns+lnt,整理一下得到：s-lns+t-lnt=2.由法一中研究的f(x)=lnx-x+1得：s-lns≥1,t-lnt≥1，所以要使得s-lns+t-lnt=2，只能s=1,t=1，所以xy=1.

总之，我们在研究双变量问题的过程，应该站在由多元化一元，由杂乱化统一的角度去思考，去尝试.

[1] 陈庆洪.浅析高考数学中的最值问题[J]. 福建中学数学,2012(01).

[2] 司麦领.函数应用题中的最值问题选解[J]. 中学生数理化(高中版·学研版),2011(05).

[3] 康小峰.高考应用性题型解析及求解策略[J]. 中学数学杂志,2011(01).

G632

A

1008-0333(2017)31-0020-03

2017-07-01

杨帆(1985.03-)，男，江苏省南通人，本科，中级职称，从事高中数学教学与研究.

杨惠民]