Pareto分布下损失分布法度量误差变动规律

莫建明,吕 刚,高 翔,卿树涛

(1.西南财经大学中国金融研究中心，四川 成都 611130；2.西南财经大学公共管理学院，四川 成都 611130；3.上海财经大学国际工商管理学院，上海 200433；4.湖南省委党校经济学部，湖南 长沙 410006)

Pareto分布下损失分布法度量误差变动规律

莫建明1,吕 刚2,高 翔3,卿树涛4

(1.西南财经大学中国金融研究中心，四川 成都 611130；2.西南财经大学公共管理学院，四川 成都 611130；3.上海财经大学国际工商管理学院，上海 200433；4.湖南省委党校经济学部，湖南 长沙 410006)

重尾分布非预期损失估计值具有不可忽视的不确定性，为此，本文以操作风险度量为例，在Pareto分布下研究损失分布法度量误差变动规律后发现：随着监管资本变动，度量误差变动具有非常高的敏感性，这意味着损失分布法度量误差具有不可预测性；在度量误差值域内，存在着多个极值风险状态点，且当操作风险趋近于这些极值状态点时，度量误差会变得非常大(以致趋于无穷大)，此时，无法准确评价度量结果的可靠性。被业界和理论界广泛使用的损失分布法存在着重大缺陷。

操作风险；损失分布法；误差传播理论；度量误差

1 引言

统计学一般用厚尾来描述分布尾部厚度，即随机变量的峰度大于3，则称随机变量对应分布为厚尾分布。但是，当该分布的k阶矩趋于无穷大时，随机变量不存在峰度，此时无法用厚尾来描述该分布尾部状态，只能采用重尾来刻画。由此可见，当描述某一分布尾部状态时，采用重尾来定义分布尾部状态更加具有一般性。在高置信度下，重尾分布的非预期损失估计具有不可忽视的不确定性，主要体现在以下两方面：

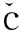
第二，非预期损失的间接度量特性会加剧不确定程度。理论上，非预期损失是在某一置信度下重尾分布的分位数，即非预期损失与重尾分布模型参数间存在某种函数关系。在以重尾性损失样本估计出这组模型参数后，根据该函数关系(度量模型)即可计算出非预期损失。显然，该非预期损失是间接度量值。在间接度量法下，重尾分布的参数估计误差会通过误差传播机制放大并形成该非预期损失的度量误差，可见，间接度量法会加剧非预期损失估计的不确定程度[2]。

由此可见，在高置信度下，重尾分布的非预期损失估计结果在客观上存在着不可忽视的不确定性。在损失分布法下，在重尾分布与损失频数分布复合而成的复合分布下估计该非预期损失，其不确定性更加显著。

损失分布法源自保险精算，2001年被用于度量操作风险，并受到业界和理论界的一致推崇。随后，巴塞尔委员会正式给出了损失分布法在操作风险度量中的定义：在操作损失事件的损失频率和损失强度有关假设基础上，对业务线/损失事件类型矩阵中的每一类操作损失的损失频率分布和损失强度分布复合成的复合分布分别进行估计，从而计算出某一时期一定置信度α下该类型操作损失复合分布的操作风险监管资本(the Operational VaR，OpVaR(α))的方法。操作风险监管资本就是复合分布的非预期损失。基于此，本文拟以操作风险为例，探讨损失分布法度量不确定性变动规律，具有非常重要的实践意义。

已有实证研究表明操作风险具有显著的重尾性。巴塞尔委员会四次操作损失数据收集的实证研究结果都表明操作风险具有显著重尾性。当以广义Pareto分布来拟合操作损失强度样本时，其形状参数大于0，即损失强度分布为Pareto分布[3]。Moscadelli[4]对巴塞尔委员会所收集的操作损失样本实证研究结果表明操作风险具有显著重尾性，同时，司马则茜等[5]实证研究我国银行业操作损失样本也得到同样结果。进一步，高丽君和高翔[6]在外部数据具有内生偏差的情况下，将外部数据调整后纳入内部数据，通过变阈值选择将损失分为主体和尾部两个部分来度量操作风险后发现，操作损失样本尾部分布为重尾性的Pareto分布。可以证明，在广义Pareto分布中，仅Pareto分布为重尾分布。因此，本文在Pareto分布下研究损失分布法度量误差随监管资本变动的特征，具有重要的理论意义和实践意义。

已有实证研究表明操作风险监管资本度量结果存在不可忽视的不确定性。Carrillo-Menéndez和Suárez[7]分别以不同度量模型度量操作风险监管资本发现，最大负偏差为-30.54%，最大正偏差为462.20%，显然该模型偏差不可忽视。在同一度量模型下，模型参数估计存在显著的不确定性(误差)，在间接度量法(非预期损失估计方法)下，重尾分布的参数估计误差会通过误差传播机制放大并形成该非预期损失的度量误差。由此可见，监管资本度量不仅存在不可忽视的模型偏差，而且在同一度量模型下也存在显著度量误差。

Opdyke[8]将操作风险监管资本度量不确定性的影响因素归纳为三方面：一是损失强度分布的重尾性大小：重尾性分布都是以截尾分布来拟合，与非截尾分布相比，截尾分布会导致更大的度量偏差；二是置信度大小：监管资本估计的置信度(99.9%)非常高，其度量偏差非常大；三是损失强度分布特征参数估计的方差大小：损失样本量越大，分布特征参数方差越小，监管资本度量误差越小。这些影响因素使损失分布模型及其特征参数估计产生不确定性，导致监管资本出现模型偏差和度量误差：

(1)模型偏差主要有两类：一是样本外的外推产生的模型偏差。操作风险具有显著重尾性，单个金融机构的损失样本量不能满足度量要求，可能导致样本外的外推问题。为此，巴塞尔协议要求高级计量法必须在共享内外部损失的数据库下进行度量。但是，即使在共享数据库下尾部损失样本也很难满足高置信度下的度量要求，不能避免样本外的外推问题。这必然会导致不可忽视的模型偏差，引起度量结果的不确定性[9]。二是样本内的模型偏差。为增加损失样本量，采用共享数据库会引起新问题：首先，不同金融机构记录操作损失样本的门槛可能存在差异，这必然使操作损失分布模型及其特征参数估计出现偏差，进而导致模型偏差[10]；其次，来自不同金融机构的操作损失样本存在异质性问题，会导致严重模型偏差[11]。可见，为解决样本外的外推问题而采取共享数据库办法，导致了新的模型偏差。

(2)损失分布特征参数估计方差导致的度量误差。已有实证研究发现当以Pareto分布拟合操作损失强度时，置信度越大，形状参数的估计方差越大，尤其在置信度99.9%下形状参数的估计方差非常大[3]。进一步的研究发现损失强度分布特征参数估计方差会对监管资本度量误差产生巨大影响，操作损失样本量越少，损失强度分布特征参数估计方差越大，监管资本度量误差越大[9]。可见，操作损失分布特征参数估计的不确定性(方差)导致了监管资本不可忽视的度量误差。

由此可见，监管资本度量不确定性主要来自模型偏差和度量误差。在现有理论下，模型偏差是无法预测的，仅模型参数估计误差所导致的度量误差可以预测。因此，在度量模型确定的条件下，模型偏差不变，仅度量误差发生变动。已有文献从以下两方面对监管资本度量误差进行了系统研究：

第一，监管资本度量误差传播机理。King[2]认为操作风险不能直接度量，只能间接度量，在操作风险度量结果及其所依赖的一组度量值之间存在某种函数关系，通过对该度量模型的研究，根据误差传播法则，就可以预测操作风险的度量误差。进一步对操作风险监管资本度量误差预测原理的深入研究发现，损失分布特征参数的估计误差会传导形成监管资本度量误差[9]。但是，两文献都未构建出操作风险度量误差的预测模型。以此为基础，莫建明和周宗放[12]假设操作损失强度为Weibull分布，系统探讨了监管资本度量误差的合成机理：损失样本分布特征参数的误差经误差传播系数的传导，合成操作风险价值的误差。操作风险度量误差传播机理为进一步探索其变动规律奠定了理论基础。

第二，监管资本度量误差变动规律。根据度量误差传播机理，已有文献主要从置信度和损失分布特征参数两个角度探讨了度量误差变动规律：①置信度变动对度量误差的影响：Gourier和Farkas等[3]实证研究发现，监管资本在置信度为0.85-0.92时比较稳定，但当置信度超过0.92后，随着置信度递增，监管资本变得非常不稳定，其度量不确定性增强。莫建明和周宗放[12]以仿真方法分析表明，随着置信度递增，操作风险监管资本度量误差加速递增，在高置信度下该度量误差不可忽视。②损失分布特征参数变动对度量误差的影响：莫建明和周宗放[13]以仿真方法分析发现，在高置信度下，操作风险价值置信区间长度随形状参数递增而递增，且形状参数是操作风险价值置信区间长度的关键影响参数。Degen[14]以仿真方法分析发现，随着损失频数参数递增，监管资本度量误差急剧递增。

以上文献仅分析了置信度或损失分布特征参数对度量误差的影响，但度量误差大小是相对于监管资本大小而言的，只有研究度量误差随监管资本变动的规律，才能准确评估度量误差大小。为此，本文拟假设操作损失强度为Pareto分布，进一步在损失分布法下研究操作风险度量误差变动规律，进而探寻重尾极值模型下损失分布法度量误差变动的一般规律。

2 监管资本及其度量误差公共影响因子

由于监管资本与其度量误差的影响因子来自其度量模型，因此，以下分别从监管资本度量模型及其度量误差的预测模型两方面探寻公共影响因子。

首先，分析监管资本的影响因子。在损失分布法下，操作风险监管资本(the Operational VaR，OpVaR(α))的解析解在一般分布情况下是无法获得的，Bocker[15]研究发现，在操作损失强度为重尾性分布的情况下，当以损失分布法度量该操作风险复合分布的尾部风险时，监管资本存在解析解。已有实证研究表明，操作损失强度为重尾性分布，尤其很接近于Pareto分布[3-6]；新巴塞尔协议规定，监管资本的度量是在置信度α为99.9%的条件下来进行，即是估计复合分布尾部的OpVaR(α)。因此，操作风险监管资本OpVaR(α)存在解析解：

(1)

式中：Δt表示估计OpVaR(α)的目标期间；α表示由损失强度分布和损失频率分布复合成的复合分布的置信度；F(()表示操作损失强度累积分布函数；EN(Δt)表示当目标期间为Δt时操作损失频数的期望值(为讨论方便，以下用符号μ替换EN(Δt))。

Embrechts和Klüppelberg[16]研究表明度量重尾性风险的最佳方法是极值模型，在金融机构，操作损失发生的频率一般比较低，尤其是损失分布尾部的损失发生频率更低，因此，一般用广义Pareto分布模型拟合操作损失强度分布。当不考虑位置参数(不影响本文研究结果)时，广义Pareto分布为：

(2)

式中：x表示操作损失强度；θ表示Pareto分布尺度参数；ξ表示Pareto分布形状参数。

将式(2)代入式(1)，可得监管资本(即操作风险价值，OpVaR(α))

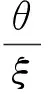
(3)

由式(3)可知，在置信度α一定情况下，监管资本的影响因子为损失分布特征参数：尺度参数θ、形状参数ξ、频数参数μ。

其次，探讨监管资本度量误差的影响因子。根据OpVaR(α)误差传播法则[2,9]，在不考虑ξ、θ、μ之间相关性条件下，得出OpVaR(α)的误差如下：

(4)

式中，σξ、σθ及σμ分别表示ξ、θ、μ的估计误差(标准误)。

由式(4)可得监管资本置信区间为[OpVaR(α)±τσOpVaR]，其中τ为某一置信度下的置信系数。决定度量误差(置信区间长度2τσOpVaR)的变量有两个：(i)置信系数τ，由主观设定的置信度决定；(ii)OpVaR(α)标准差σOpVaR，由分布特征参数标准差和误差传播系数共同决定。可见，在分布特征参数标准差(σξ、σθ及σμ)一定的条件下，度量误差唯一的客观影响因子为误差传播系数。

根据误差传播法则的基本原理，定义操作风险监管资本度量误差传播系数如下：

定义1 误差传播系数是指分布特征参数(ξ、θ、μ)的标准差合成到OpVaR(α)的标准差中去的比例。分布特征参数ξ、θ、μ的误差传播系数分别为：

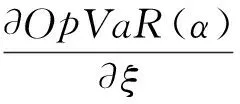
将式(3)代入定义1，可得分布特征参数的误差传播系数cξ、cθ、cμ分别为：

(5)

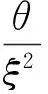
(6)

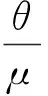
(7)

由定义1及式(5)～(7)可知，在置信度α一定的条件下，误差传播系数的唯一影响因子为损失分布特征参数。因此，在置信系数τ一定条件下，监管资本度量误差唯一的客观影响因子为损失分布特征参数ξ、θ、μ。

综合以上两方面分析可知，监管资本与其度量误差存在公共影响因子：分布特征参数ξ、θ、μ。通过探讨监管资本与其度量误差随分布特征参数变动的规律，可得度量误差随监管资本变动规律。

3 操作风险度量误差变动特征

3.1 理论模型

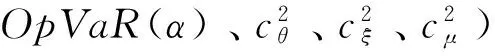
根据命题1和命题2发现，不管是尺度参数还是形状参数变动，都存在规律：随监管资本递增，度量误差越大，反之亦然。这意味着，当操作损失强度为重尾分布Pareto分布时，尽管是在由操作损失强度分布和损失频数分布复合而成的复合分布下度量操作风险监管资本，但是，损失强度分布特征参数对监管资本及其度量误差的影响规律，仍然与在单一Pareto分布下的影响规律相同。

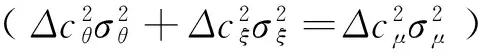
在广义Pareto分布中，只有Pareto分布属于重尾分布，其形状参数表征分布的尾部特征，又称为尾指数，形状参数越大，分布尾部越厚。当ξ=1时，Pareto分布成为一个特殊分布，被称为幂分布，属于典型的标准重尾分布。由命题3可知，在临界点ξ=1左右，损失强度分布具体不同的尾部形态，度量误差变动趋势存在显著差异：

当ξ>1时，Pareto分布尾部厚度比幂分布尾部厚，此时，大于一阶矩都不存在，无法估计其峰度，此时，在频数参数影响下，随着监管资本递增，度量误差增大，反之亦然。

当ξ<1时，Pareto分布尾部厚度比幂分布尾部薄，此时，在频数参数影响下，随着监管资本变动，度量误差变动极其敏感，其变动趋势线是一条存在多个极值状态点的曲线。

因此，损失频数变动对度量误差的影响规律，与损失强度分布的尾部形态有关。在不同损失强度分布尾部形态下，度量误差变动特征完全不同。

综合上述命题1～命题3所得结果可知，随着操作风险增大，监管资本递增，在损失强度分布特征参数影响下，度量误差增大，在频数参数影响下，度量误差变动呈现出显著的敏感性，其变动趋势曲线存在多个极值风险状态点。这意味着在某些风险状态下，度量误差可能变得非常大(极大值)。

3.2 实例检验

由于操作损失数据的机密性，目前没有公开的操作损失专业数据库可供研究，因此，本研究根据已有文献实证拟合所得操作损失分布的特征参数值，对上述理论进行检验。到目前为止，在所有对巴塞尔委员会收集的操作损失数据(Loss Data Collection Exercise)的研究中，唯有Moscadelli(2004)[4]的实证研究全面地对业务线BL1～ BL8的操作损失频数分布和损失强度分布进行了拟合，并估计出特征参数值，如表1所示。根据BASELⅢ定量标准规定，在以下实例分析中，设α=99.9%。

由命题1知，监管资本及其度量误差相对于尺度参数的灵敏度为常数，因此，验证命题2，在形状参数影响下，度量误差变动趋势。假设α=99.9%，得如下表1。

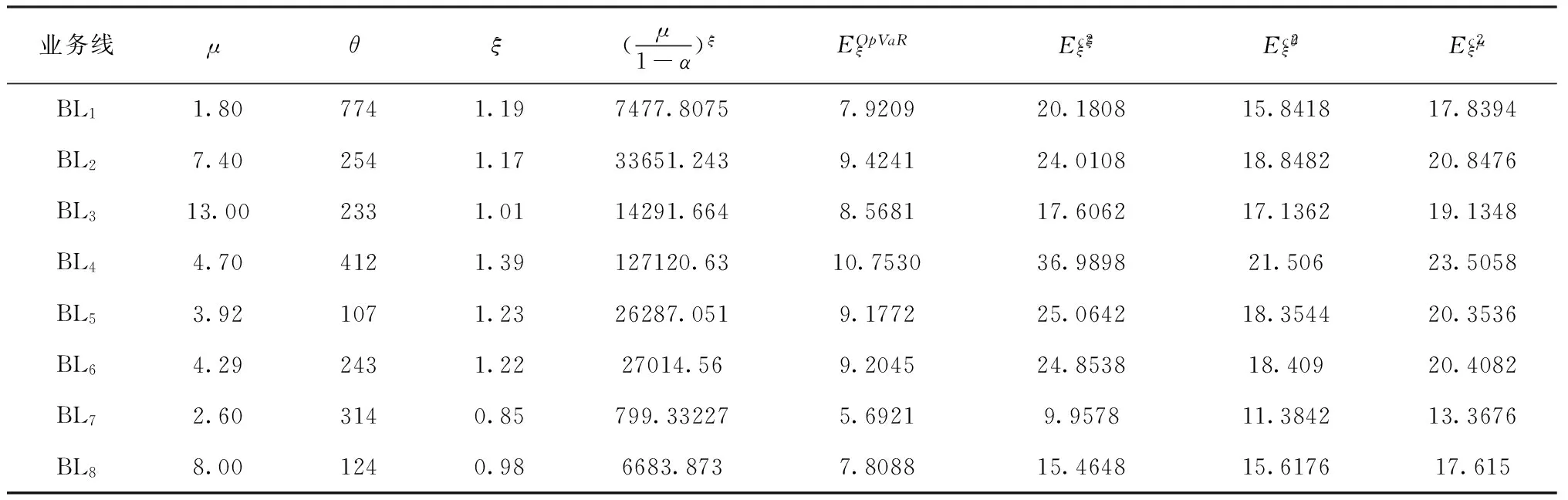
表1 在形状参数影响下监管资本及其度量误差变动趋势

注：1、表中参数μ、ξ、θ的数值来自文献Moscadelli[4]；2、业务线BL1-BL8的分类是以BASELⅡ为分类标准

由表1有如下结论：

2)业务线BL1～ BL8的操作损失强度分布具有显著重尾性，即操作风险具有显著重尾性。统计学一般用峰度来描述分布尾部厚度，即随机变量的峰度大于3，则称随机变量对应分布为厚尾分布。但是，当该分布的3阶矩趋于无穷大时，随机变量不存在峰度，此时无法用峰度来描述该分布尾部状态，只能采用重尾性来刻画。由表1可知，存在ξ>1/3，所有业务线的损失分布都不存在峰度，因此，只能用重尾性来定义，不能用峰度来定义。这意味着，所有业务线损失分布的尾部厚度比一般的能够用峰度来定义的分布都要厚得多。

上述分析表明，本文所得命题具有实践意义，该实例所有业务线损失强度分布具有重尾性，在形状参数影响下，随监管资本递增，度量误差递增。

然后，验证命题3，在频数参数影响下，度量误差变动趋势。假设α=99.9%，可得表2如下。

由表2可知，损失强度分布形状参数变动范围在0.85～1.39之间，其三阶矩都不存在，其厚尾程度仅仅比幂分布(当ξ=1时)略薄(BL7～BL8)或略厚(业务线BL1～ BL6)，但是，其度量误差变动趋势却有完全不同的两种情况：

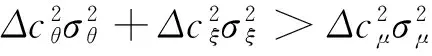
上述实例分析表明，在频数参数影响下，随监管资本递增，针对业务线BL1～ BL6，其度量误差增大，针对业务线BL7～ BL8，度量误差变动趋势曲线存在着多个极值状态点。

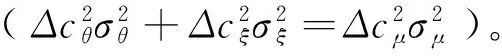
表2 在频数参数影响下监管资本及其度量误差变动趋势

4 结语

已有实证研究表明操作风险具有显著重尾性。在高置信度下，当以损失分布法来度量重尾性操作风险时，其度量结果存在不可忽视的不确定性。为此，本文假设操作损失强度为Pareto分布，应用损失分布法度量操作风险，通过系统研究获知监管资本度量误差变动的规律：随着操作风险增大，监管资本递增，在损失强度分布特征参数影响下，度量误差递增；在频数参数影响下，当ξ≥1时，度量误差递增，当ξ<1时，度量误差变动趋势曲线存在多个极值状态点。

由此可见，随着监管资本变动，度量误差变动具有非常高的敏感性，这意味着监管资本度量误差具有不可预测性；在度量误差值域内，存在着极值状态点，且在这些极值风险状态下，相对于监管资本来说，度量误差会变得非常大(以致趋于无穷大)，此时无法准确评价度量结果的可靠性。可见，当损失强度分布为重尾性分布，在高置信度下使用损失分布法，其度量结果可能出现严重缺陷。本研究进一步探明了当损失强度具有显著重尾性时，损失分布法度量误差的变动规律，为该方法在重尾性风险度量中的应用奠定了理论基础。

附录

附录A，命题1证明过程：

附录B，命题2证明过程：

证明：将(3)式代入定义2，可得

(B1)

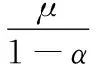
将(5)式代入定义2，可得：

(B2)

(B3)

(B4)

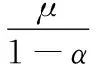
附录C，命题3证明过程：

证明：将(3)式代入定义2可得：

(C1)

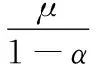
(C2)

(C3)

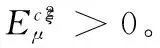
(C4)

[2] King J L. Operational risk: Measurement and modelling[M]. New York: John Wiley&Sons, Ltd, 2001.

[3] Abbate D,Gourier E,Farkas W.Operational risk quantification using extreme value theory and copulas: From theory to practice[J]. The Journal of Operational Risk, 2009,4(3):3-26.

[4] Moscadelli M. The modelling of operational risk: Experience with the analysis of the data collected by the Basel Committee [R]. Banca D’Italia,2004.

[5] 司马则茜, 蔡晨, 李建平. 度量银行操作风险的POT幂律模型及其应用[J]. 中国管理科学, 2009, 17(1): 36-41.

[6] 高丽君, 高翔. 基于混合数据的银行操作风险参数混合模型分析[J]. 中国管理科学, 2017, 25(5): 11-16.

[7] Carrillo-Menéndez S, Suárez A. Robust quantification of the exposure to operational risk: Bringing economic sense to economic capital[J]. Computers &Operations Research, 2012, 39(4):792-804.

[8] Opdyke J D. Estimating operational risk capital with greater accuracy, precision, and robustness[J]. the Journal of Operational Risk, 2014,9(4):3-79.

[9] Mignola, G. and Ugoccioni, R. Sources of uncertainty in modelling operational risk losses[J],.The Journal of Operational Risk, 2006,1(2):33-50.

[10] Baud N, Frachot, A, Roncalli T. How to avoid over-estimating capital charge for operational risk? [R]. Working paper,Credit Lyonnais Bank,2003.

[11] Na H S, Van. D B J, Miranda L C,et al. An econometric model to scale operational losses[J]. Operational Risk, 2006, 1(2): 11-31.

[12] 莫建明, 周宗放. LDA下操作风险价值的置信区间估计及敏感性[J]. 系统工程, 2007,25(10): 33-39.

[13] 莫建明, 周宗放. 操作风险价值及其置信区间灵敏度的仿真分析[C]//第六届中国管理科学与工程论坛. 2008中国发展进程中的管理科学与工程. 上海市：上海财经大学出版社, 2008：5月23日-26日. 313-317.

[14] Degen M, The calculation of minimum regulatory capital using single-loss approximations[J]. The Journal of Operational Risk，2010，5(4)：3-17.

[15] Bocker, K. Operational risk analytical results when high-severity losses follow a generalized Pareto distribution (GPD)[J]. Risk of London, 2006, 8(4): 117-120.

[16] Embrechts P, Klüppelberg C， Mikosch T. Modelling extremal events for insurance and finance[M], Berlin:Springer,1997..

Change Rule of Loss Distribution Approach’s Measurement Error underthe Pareto Distribution

MOJian-ming1,LVGang2,GAOXiang3,QINGShu-tao4

(1. Chinese Finance Research Institute of SWUFE, Chengdu 610074,China;2. The School of Public Administration of SWUFE, Chengdu 611130,China;3. School of International Business Administration, SHUFE, Shanghai 200433,China;4. Hunan provincial Party School Department of Economics, Changsha 410006,China)

According to the extreme value statistical theory, unexpected loss estimation in a heavy-tailed distribution objectively has uncertainty that cannot be neglected in a high confidence level. Existing empirical research shows that the operating loss intensity distribution has a significant heavy-tailed quality. Therefore, under the loss distribution approach, namely in the composite distribution compounded of heavy-tailed operating loss intensity distribution and loss frequency distribution, the regulatory capital of operational risk is in great uncertainty that cannot be neglected. The uncertainty of regulatory capital is mainly from model error and measurement error. In the existing theory, the model biases are unpredictable, and only the model parameter estimation error caused by the measurement error can be predicted. Therefore, in the condition of fixing measurement model and the model deviation is invariable, only the measurement error changes.

Theoretical research shows that only Pareto distribution is heavy-tailed distribution in the generalized Pareto distribution. Therefore, the operational risk measurement is taken for example in this paper. After measuring error variation by loss distribution approach in Pareto distribution, it is found: As the operational risk increases and the regulatory capital increases progressively, and under the influence of characteristics parameters of loss intensity distribution, the measurement error increases. Under the influence of frequency parameters, when the shape parameter is greater than 1, the measurement error increases. However, when the shape parameter is less than 1, the measurement error trend line has multiple extreme points. Furthermore, according to the fitting results of operating loss frequency distribution and loss intensity distribution using the Basel committee operating loss data samples, they can verify the validity of the proposed theoretical model in this paper.

Thus’ it can be seen that with the changes in regulatory capital, the measurement error changes in high sensitivity, and this means that the measurement error of regulatory capital is unpredictable. Within the range of measurement error, there exists the extreme points, and in the condition of these extreme risk, the measurement error becomes very large (tends to infinity) in relative to the regulatory capital. At this moment, the reliability of the measurement results cannot be accurately evaluated. Obviously, when loss intensity distribution is a heavy-tail distribution, the measurement results may appear serious faults with the loss distribution approach in a high confidence level. Furthermore， the regularity of error variation measured by loss distribution approach when the loss intensity has a significant heavy tail and lays a theoretical foundation for applying LDA in heavy-tailed risk measurement is explored.

operational risk; loss distribution approach; error propagation theory; measurement error

1003-207(2017)11-0134-09

10.16381/j.cnki.issn1003-207x.2017.11.014

F830；TP202

A

2016-02-01；

2017-04-17

国家自然科学基金资助项目(71171167,71501117,71671144,71373213,71301130); 教育部项目(16YJA790038, 13YJC790024); 国家社科基金重大项目资助项目(13&ZD030)

莫建明(1970-)，男(汉族)，四川眉山人，西南财经大学中国金融研究中心副教授，研究方向：金融工程、金融风险，E-mail: mojm@swufe.edu.cn.