基于双限制优势粗糙集的高校学生心理危机预警要素分析

张 勇， 刘心报，赵丽欣，夏晶凡， 张 丽

(1.合肥工业大学管理学院，安徽 合肥 230009；2.合肥工业大学电气与自动化工程学院，安徽 合肥 230009；3.合肥工业大学智能制造技术研究院,安徽 合肥 230009；4.合肥工业大学纪委办、监察处，安徽 合肥 230009)

基于双限制优势粗糙集的高校学生心理危机预警要素分析

张 勇1,4， 刘心报1，赵丽欣2，夏晶凡3， 张 丽2

(1.合肥工业大学管理学院，安徽 合肥 230009；2.合肥工业大学电气与自动化工程学院，安徽 合肥 230009；3.合肥工业大学智能制造技术研究院,安徽 合肥 230009；4.合肥工业大学纪委办、监察处，安徽 合肥 230009)

为了有效识别大学生心理危机，根据教育统计学理论，采用优势关系分类方法，建立了不完备偏序大学生心理危机预警信息系统的双限制优势粗糙集模型和计算方法。给出了根据信息系统每个属性各自的已知属性值，进行概率分布的计算，选定概率阈值，与已获得的优势概率进行比较，实现对象间的优势关系判断，完成双限制优势关系的分类。并通过改变阈值概率，较全面地比较分析不同概率水平下的属性约简效果，从而获取大学生心理危机的引致要素。通过问卷调查和对比分析计算，表明该方法获取的约简结果更具适用性，且具有更高的准确性和更低的分类误判率。

不完备性；限制优势关系；优势概率；双限制优势关系

1 引言

大学生心理危机的控制和应对是建立在准确的识别与预警基础上[1]。降低心理危机预警信息系统指标之间的相关性和冗余性，是识别危机信号、降低危机成分行之有效的方法之一[2]。目前，主要采用主观方法评定大学生心理危机，从心理、社会等指标构建心理危机预警指标体系，即通过问卷调查和量表测评来主观地识别心理危机。主观评定法的评分标准不一，往往这些指标较模糊，且数据采集困难、易受主观因素等影响，致使预警指标体系获取的信息往往具有遗漏型[3]未知属性值，同时含有大量的偏好关系属性，难以对其进行科学计算和动态评定，从而使得研究难度较大。

随着粗糙集理论的出现，心理危机的预警和有效识别已成为可实现的目标和新的发展趋势(Dominance-based Rough set Approach，DRSA)。中Greco[4]等提出了一种优势粗糙集方法，以解决偏序属性的分类问题，但其条件是完备信息系统对象间的关系、性质及属性约简。Yang Xibei等[5]将相似关系[6]与优势关系结合，提出的相似优势关系假定了属性空值可以等于任意属性实值[7]，从而存在划分粒度过大的缺陷。翟育明等[8]中采用集对限制相似优势粗糙集模型研究了属性取值符合均值概率分布情况下的属性约简，一定程度上降低了分类误判率，但未考虑属性实值优于属性空值“*”的情况，使得分类仍然存在较高的误判率。骆公志等[9]提出了一种限制优势关系约简模型，认为只有属性极大值优于属性空值“*”，但次极大的属性值仍有优于属性空值的可能，而骆公志等[9]的限制条件过于严格，易将实际满足条件的对象误判为不属于同一个决策类，从而增加分类的误判率。针对偏好关系属性这类问题，运用属性最小约简方法并结合优势关系、限制优势关系下分类划分原则即可有效解决[10]。同时，教育统计学统计规律和社会学统计数据[11]也证明了学生在某些行为特征和心理特征上具有一定的正态分布、离散均匀分布等类型的分布趋势。

本文结合高校学生心理危机预警指标体系的属性值的概率分布特点，将正态分布和离散均匀分布引入基于限制优势关系粗糙集的属性约简，建立了大学生心理危机信息系统的双限制优势关系属性约简模型和计算方法，获取大学生心理危机的引致要素。(1)根据每个属性各自的已知属性值，进行概率分布的计算，获取每个属性中未知属性值优于已知属性值的概率大小和已知属性优于未知属性的优势概率。(2)选定概率阈值，与已获得的优势概率进行比较，实现对象间的优势关系判断，完成双限制优势关系的分类。(3)连续的属性值可获取更精确的概率统计信息，同时，在连续属性下也可进行优劣关系的判断，且对象的分类更加准确。实例约简结果表明，该方法能有效地进行属性约简，其具有更高的准确性和更低的分类误判率。

2 大学生心理危机预警信息系统的双限制优势关系粗糙集属性约简模型

2.1 大学生心理危机预警信息系统的双限制优势关系

依据高校学生的学习成绩、智力水平、心理状态等都服从正态分布，年级、生源地等服从离散均匀分布的统计规律，根据每个属性各自的已知属性值，进行概率分布的计算，获取每个属性中未知属性值优于已知属性值的概率大小和已知属性优于未知属性的优势概率，构建双限制优势关系。

设Θ=为一不完备偏序高校学生心理危机预警信息系统，其中U={x1,x2…,xn}是论域，对应学生群体，x1,x2,...,xn表示n个学生；C是条件属性集，对应学生心理危机事件诱发因素的集合；D是决策属性集，对应各种具有危害性的心理危机事件；f为U×(C∪D)的映射，为论域对象的属性指定唯一值。

定义1 在不完备偏序高校学生心理危机预警信息系统Θ=中，从条件属性集C中任意选取条件属性集的子集P(P⊆C)，关于的双限制优势关系定义为：

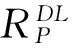
∨(f(xi,al)=*∧f(xj,al)=ν,pl(xi,xj)≥p)

∨(f(xi,al)=ν∧f(xj,al)=*,pl(xi,xj)≥p)

∨(f(xi,al)=*∧f(xj,al)=*,pl(xi,xj)≥p)}

(1)

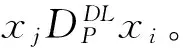
性质1 多重限制优势关系为二元关系，具有自反性，但不一定满足对称性和传递性。

定义2 在不完备偏序高校学生心理危机预警信息系系统Θ=中，对于一个学生对象xi(xi∈U)，在条件属性集P(P⊆C)下，该学生对象xi的P-双限制优势集和P-双限制劣势集定义如下：

(2)

定义3 在不完备偏序高校学生心理危机预警信息系统Θ=中，对于决策属性集中的一个决策属性d(d∈D)，该决策属性值集为Vd(Vd=T,T={1,2…,n})，根据此决策属性值集，将论域中所有学生分为类，对于每一个t∈T，在该分类下的学生集合为Dlt={x∈U:f(x,d)=t}，所有分类集合的并集即对应整个论域的学生Dl1={x∈U:f(x,d)=t}。同时我们定义，对于任意的t和s(t∈T,s∈T)，假设Dl1中的元素优于中的元素，则分类Dl1的上向并集和下向并集如下:

(3)

2.2 双限制优势关系的属性约简

粗糙集理论中的属性约简算法种类多，考虑到高校学生心理危机预警信息系统是优势关系下的不协调信息系统，而文献[12]的部分一致约简算法适合该类信息系统，且该算法是基于分辨矩阵的约简算法，在论域中对象较多的情况下，能够有效降低计算量，提高约简的效率，故本文在使用双限制分类规则进行分类后，结合该算法进行双限制优势关系下的条件属性特征简约。

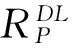
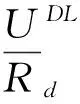
(4)

其中，称δP(x)为论域U上的关于条件属性子集P的部分一致函数。

定义5 在不完备偏序高校学生心理危机预警信息系统Θ=中，计算获得论域中每个学生对象在条件属性子集P部分一致函数，并记

(5)

用f(x,a1)表示学生对象关于属性的取值。定义

(6)

其中，称Dδ(xi,xj)为xi与xj的部分一致可辨识属性集，将其作为可分辨矩阵的元素，所有的部分一致可辨识属性集构成矩阵，Mδ=(Dδ(xi,xj),xi,xj∈U)我们称该矩阵为高校学生心理危机预警决策信息系统的部分一致辨识矩阵。

定义6 在不完备偏序高校学生心理危机预警信息系统Θ=中，对部分一致辨识矩阵Mδ的元素进行析取和合取的计算，即：

(7)

称为该预警信息系统的部分一致辨识公式。

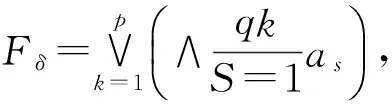
3 大学生心理危机预警要素双限制优势关系条件属性约简计算方法

输入：一个不完备偏好预警信息系统Θ=，C是条件属性，D是决策属性。

输出：此决策信息系统的在所取阈值概率下的最小部分一致约简。

步骤1：构建决策表。确定条件属性C={a1,a2,…,an}，决策属性D={d1,d2,…,dm}；结合典型案例与问卷调查，填入属性值，完成决策表的构建。

步骤2：计算优势概率。确定每个属性的概率分布，即正态分布或者离散均匀分布，根据已知属性值进行参数估计，确定概率分布函数，结合概率分布函数计算已知属性值优于未知属性值的概率。

步骤3：选定阈值概率，获取条件属性集的部分一致函数。并由定义1进行论域中对象的双限制优势关系的分类，在结合定义3和定义4计算得到每个对象在条件属性集下的部分一致函数δC(xi){i=1,2,…,n}。

步骤4：构建部分一致辨识矩阵。再由定义5计算得到xi和xj的部分一致可辨识属性集，构建部分一致辨识矩阵Mδ。

步骤5：获取部分一致约简。按照公式6，构建区分函数Fδ，使用分配率、吸收律对部分一致辨识公式进行极小析取范式的化简，最终获取该阈值概率下决策表的全部部分一致约简。

步骤6：转到步骤3，改变阈值概率，直到获取最小的部分一致约简集，终止计算。

4 算例分析

有关高校学生极端心理危机预警的文献以及相关研究机构公布的数据中，无大量详实的高校学生基本资料、心理健康状态等信息，这些数据主要可能涉及到个人隐私。但近年来，以自杀和重度伤人为代表的大学生极端心理危机事件频发，严重危害大学生的健康成长，如何高效预防和干预极端心理危机事件以促进大学生健康成长、全面成才刻不容缓。为能获得真实可靠的数据，本文结合高校学生极端心理危机诱发因素的一些理论研究成果，在段鑫星提出的《大学生压力源问卷》基础上，根据高校实际情况，研制了大学生极端心理危机调查问卷，问卷包括来源地、是否失恋、抑郁自评得分、人际关系、学习成绩、专业满意度、学习压力、就业压力、健康状况9个题项。鉴于极端心理问题的学生在高校所占的比例极小，故向安徽某工科全国重点大学新生心理健康水平普测的分析结果中具有重度心理危机的学生发放问卷13份，成功回收13份，并根据问卷收集的数据构建如下决策信息表1。

本文对含有定性描述的信息表的量化如下：

(1)学生来源为2级评定(农村=1，城镇=2)；

(2)是否失恋为2级评定(是=1，否=2)；

(3)人际关系、健康状况为4级评定(优秀=3，良好=2，一般=1，较差=0)；

(4)专业满意度为4级评定(非常满意=3，比较满意=2，一般=1，不满意=0)；

(5)学习压力、就业压力为4级评定(较小=3，一般=2，较大=1，很大=0)；

(6)心理危机程度(一级=2，二级=1，三级=0)；

(7)学习成绩使用平均学分绩点{GPA=∑(课程学分×课程绩点)/修读课程的学分总数}进行综合评价；

(8)未知=*。

通过量化后，获得量化决策信息表如表2。

表1 决策信息表

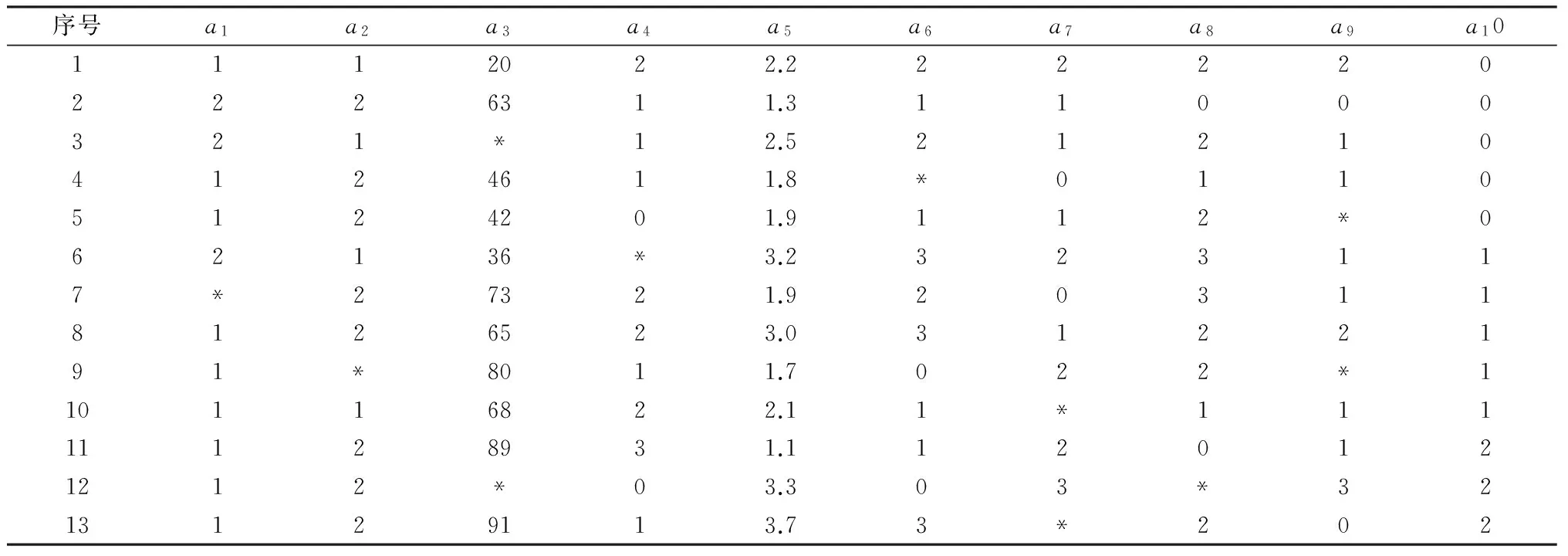
表2 量化决策信息表

4.1 双限制优势粗糙集法分析

为分析不同的阈值概率取值对于属性约简结果的影响作用，选取一组阈值概率值，即{1，0.9，0.8，0.7，0.6，0.5，0.4，0.3，0.2，0.1，0}，在MATLAB2010b环境下，循环输入阈值概率，并获得属性约简结果，见表3。

从双限制优势粗糙集的属性约简结果可知，在阈值概率为0.9和0.8的水平，部分一致约简集达到最小集，最小集包括抑郁自评得分、人际关系、学习压力三项指标。在高校学生极端心理危机的研究中，对于具有自杀意念的这类极端心理危机的学生，统计数据分析表明，其抑郁程度显著高于不具有自杀意念的学生[13]，一旦这种抑郁情绪没有得到及时有效的治疗，就有可能引发自杀行为这样更加严重的后果，可见，抑郁情绪对于学生的心理危机的发展具有重大影响。而Tang Fang和Qin Ping[14]通过对5972名中国在校大学生进行调查分析得到，交往能力差所导致人际关系缺乏是引发学生自杀意念的重要危险因素。双限制优势粗糙集的属性约简剔除了就业压力、生源地等的6项指标，这个结果并非表明这些指标对于学生极端心理的发展没有影响。Order等[15]的研究分析指出，不同的研究者所得到的结论并不完全一致，未就业与自杀事件之间的关系仍不明确。本文的约简模型将工作压力这一项剔除，这可能是因为研究对象涵盖所有年级，而其中面临就业压力的学生只占小部分，就业压力对于心理危机影响的特异性并不明显。同时，YouZhipi等[16]中的统计分析结果表明，来自农村的学生自杀率低于城镇的学生，然而，在安徽某工科全国重点大学这样的理工科院校，农村和城镇学生的分布比例较均匀，不同于一些艺术类学校具有明显的比例特征，其对于学生极端心理危机影响的特异性也不明显。所以，相对就业压力、生源地等指标，抑郁自评得分、人际关系、学习压力这三项指标对于安徽某工科全国重点大学在校学生的心理危机影响更具代表性，与统计学的研究结论比较分析，双限制优势粗糙集的约简结果具有参考性。

表3 双限制优势关系属性约简

4.2 限制优势粗糙集法分析

依据文献[17]中的限制优势关系下的属性约简需对连续的属性值进行离散化处理，故对抑郁自评得分和学习成绩进行离散化处理，其中，抑郁自评得分：无抑郁(<50分)=3，轻度抑郁(50～62)=2，中度抑郁(63～72)=1，重度抑郁(>72)=0；学习成绩：优秀(3～4)=3，良好(2～3)=2，合格(1～2)=1，不合格(<1)=0，离散化决策信息表见表4。

表4 离散化决策信息表

采用张勇等[17]中基于限制优势关系的属性约简算法，在MATLAB环境下，获得部分一致约简集为{a2,a3,a4,a5,a6,a7,a8,a9} ，包含“是否失恋”、“抑郁自评得分”、“人际关系”、“学习成绩”、“专业满意度”、“学习压力”、“就业压力”、“健康状况”8项指标，只剔除了“生源地”一项指标。懂炳刚[18]对815位在校大学生的问卷调查进行统计分析，结果显示，社会心理学因素对自杀意念的发生起重要作用，在进行多因素分析时，身体健康状况最终未纳入多元Logistic回归模型，相对抑郁、失恋等社会心理因素，生物因素中的身体健康对学生极端心理危机的产生作用较小。而限制优势粗糙集的属性约简将健康状况与抑郁程度、人际关系等指标同时保留，未能突显出社会因素和心理因素的重要性。

4.3 相关因素法分析

相关因素分析法是一种较为成熟的统计学分析法，其处理的对象为不含有决策属性的完备信息系统，故通过均值替换法将属性空值补足，获得完备信息表，见表5。

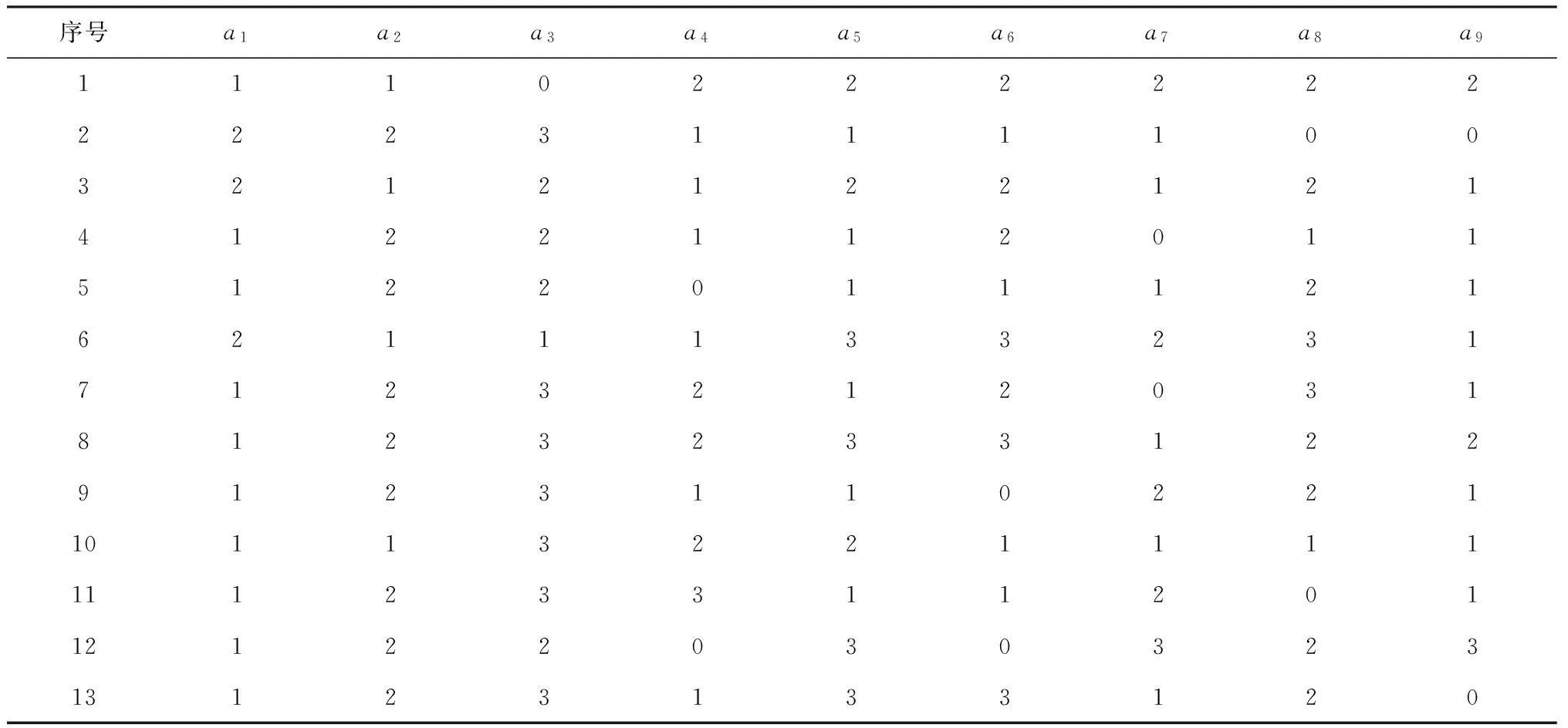
表5 完备信息表

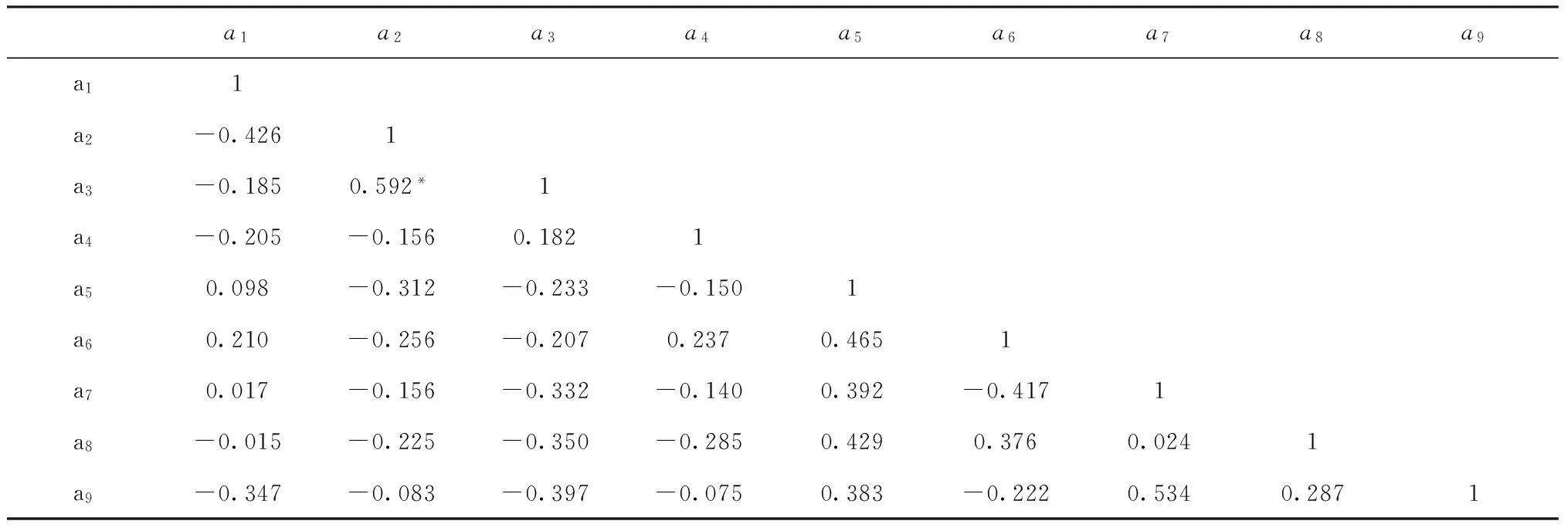
表6 相关系数表

*.在0.05水平(双侧)上显著相关

对于表5，使用spss19.0对各项指标进行相关性分析，计算获得相关系数表，见表6。

从表6的结果可知，仅“是否失恋”和“抑郁自评得分”两项指标显著相关，根据相关因素分析法中的原则，即保留显著相关指标中的一个，两项指标比较可知，学生失恋的几率较低于学习和生活引发抑郁情绪的几率，故剔除“是否失恋”这一项。结合上文分析可知，在安徽某工科全国重点大学这样的理工科院校，生源地对于学生极端心理危机的影响并不具有明显的特异性，同时社会因素和心理因素相对身体健康因素的决定性作用更大，相关因素分析法的属性约简将健康状况、生源地与抑郁程度、人际关系等指标同时保留，也未能突显出社会因素和心理因素的重要性。

4.4 高校学生心理危机引致要素条件属性约简方法的性能比较

(1)适用性能比较

通过限制优势粗糙集约简方法[17]以及相关因素分析法与双限制优势粗糙集约简方法比较可得到如下结论：(1)双限制优势关系下的部分一致约简集更小，能够剔除更多属性指标；(2)双限制优势粗糙集属性约简的最小属性集包括“抑郁自评得分”、“人际关系”、“学习压力”三项社会因素和心理因素，剔除“身体健康”、“生源地”等非心理因素，这也与文献[17]的研究结果一致，即说明本文给出的双限制优势关系能更好地识别出影响程度更大的属性指标，筛选的结果更加有效；(3)从表3可知，随着阈值概率由1到0逐渐减小，部分一致约简集呈现先减小再增大的变化过程，当阈值很高时，分类要求越严格，越接近限制优势关系，其结果也与限制优势关系下的约简相近。

(2)分类误差率比较

对于不完备偏序预警系统Θ=，a∈C,x,y∈U，属性a的属性值Va={1,2,3,4,5}，属性值符合离散均匀分布，优势关系为1<2<3<4<5。

在限制优势关系下，当时x(a)=1，y(a)=*时，y(a)优于x(a)；当x(a)=1,y(a)=1，y(a)不优于x(a)，而y(a)=*≥=2的概率为4/5，判断y(a)优于x(a)的出错率仅为1/5，故限制优势关系判断y(a)不优于x(a)的出错率为4/5。

在本文双限制优势关系下，若阈值概率为1，当x(a)=1,y(a)=*时，p(y-x)=1，y(a)优于x(a)；当x(a)=2，y(a)=*p(y>x)=0.8<1，判断结果为y(a)不优于x(a)，此时误判率也为4/5；若阈值概率为0.8，当x(a)=1,y(a)=*时，p(y>x)=1，y(a)优于x(a)；当x(a)=2,y(a)=*，p(y>x)=0.8，判断结果为不优于，此时误判率为0；对于其他阈值概率情况下误判率的比较，见表7。

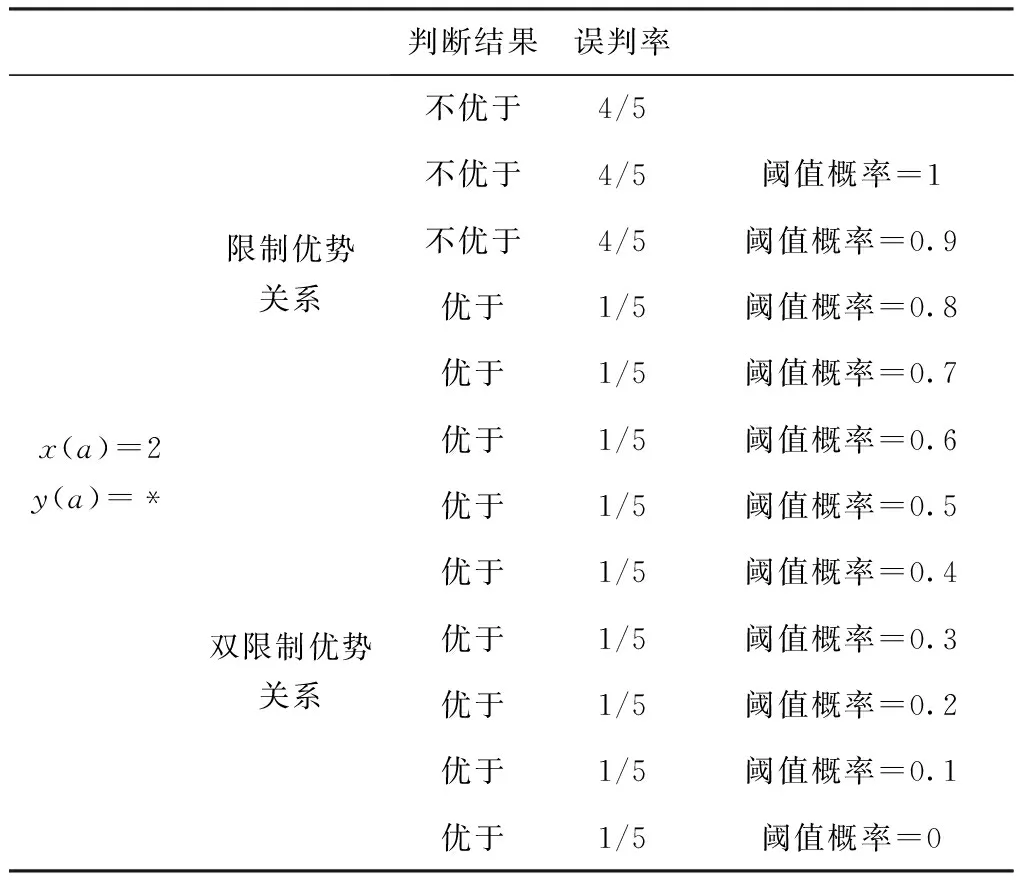
表7 分类误判率比较

从表7中的结果可知，双限制优势关系的分类误判率不会高于限制优势关系，且在大部分的阈值概率下，误判率都会低于限制优势关系的分类误判率。

5 结语

针对高校学生心理危机预警信息系统，进行了以下方面的研究。

(1)依据教育统计学的研究成果，采用优势关系分类方法给出了不完备偏序高校学生心理危机预警信息系统的双限制优势关系属性约简模型和计算方法。

(2)根据信息系统每个属性各自的已知属性值，进行概率分布的计算，选定概率阈值，与已获得的优势概率进行比较，实现对象间的优势关系判断，完成双限制优势关系的分类。

(3)通过改变阈值概率，较全面地比较分析不同概率水平下的属性约简效果，获取大学生心理危机的引致要素，最终实现预警指标系统的客观化与去冗余性的目的。

(4)通过与限制优势关系方法比较，对获取最简的约简结果进行了适用性能和分类误差率比较分析，表明该模型对于不完备偏序信息系统的属性约简具有更高的准确性和更低的分类误判率。

然而，本文仅讨论了高校学生心理危机预警要素中双限制优势关系，对等价关系和优势关系是下一步继续努力研究的方向。

[1] 董雪梅. 高校公共安全突发事件成因分析及应对策略[J]. 中国行政管理, 2009，(7)：91-94.

[2] 郭丽娟, 仪彬, 关蓉，等. 简约指标体系下的区域创新能力评价:基于主基底变量筛选和主成分分析方法[J]. 系统工程, 2011, 29(7):34-40．

[3] Grzymalabusse J W. Data with missing attribute values: Generalization of indiscernibility relation and rule induction[M] // Peters JF,Skowron A,Grzymala-Busse JW,et al.Transactions on rough sets I. Springer Berlin Heidelberg, 2004.

[4] Greco S, Matarazzo B, Slowinski R .Rough approximation by dominance relation [J].International Journal of Intelligent Systems, 2002, 17(2):153-171.

[5] Yang Xibei, Yang Jingyu, Wu Chen, et al. Dominance-based rough set approach and knowledge reductions in incomplete ordered information system[J]. Information Sciences, 2008, 178(4):1219-1234.

[6] Stefanowski J, Tsoukiàs A. On the extension of rough sets under incomplete information[C]//Proeedings of International Wrokshop on Rough Sets,Fuzzy Softs,Data Mining,and Granular,Soft Computing，Yamaguchi, Japan Computing,Yamaguchi,9-11,1999.

[7] 骆公志, 杨晓江, 刘思峰. 基于限制优势关系的粗糙决策分析模型[J].中国管理科学, 2009,17(5):127-132.

[8] 翟育明, 蔡红, 郭斌. (α,β) 集对限制优势粗糙集及决策模型[J]. 系统管理学报, 2014，23(3):437-443.

[9] 骆公志, 杨习贝, 杨晓江．基于限制优势关系的粗糙模糊集及知识约简[J]．系统工程与电子技术, 2010，32(8)：1657-1661.

[10] 苟光磊, 王国胤, 利节, 等. 基于置信优势关系的粗糙集近似模型[J]. 控制与决策, 2014,29(7):1325-1329.

[11] Galton F. Statistics of mental imagery[J]. Mind, 1880, 5(19):301-318.

[12] 徐伟华, 张晓燕, 张文修. 优势关系下不协调目标信息系统的部分一致约简[J]. 模糊系统与数学, 2009, 23(6): 155-161.

[13] Garlow S J, Rosenberg J, Moore J D, et al. Depression, desperation, and suicidal ideation in college students: Results from the American Foundation for Suicide Prevention College Screening Project at Emory University [J]. Depression and Anxiety, 2008, 25(6):482-488.

[14] Tang Fang, Qin Ping. Influence of personal social network and coping skills on risk for suicidal ideation in Chinese university students. [J]. Plos One, 2015, 10(3):e0121023.

[15] Orden K A V, Witte T K, Cukrowicz K C, et al. The interpersonal theory of suicide [J]. Psychological Review, 2010, 117(2):575-600.

[16] You Zhiqi, Chen Mingxi, Yang Sen, et al. Childhood adversity, recent life stressors and suicidal behavior in Chinese college students.[J]. Plos One, 2014, 9(3):e86672.

[17] 张勇, 张丽, 王建平. 基于限制优势关系粗糙集的高校学生心理危机预警要素分析[J]. 合肥工业大学学报,2013,36(12):1523-1528.

[18] 董炳刚. 心理扭力与大学生自杀意念关系的研究[D].济南：山东大学,2014.

The Early Warning Factor Analysis of Psychological Crisis of College StudentsBased on Double Limited Dominance Rough Set

ZHANGYong1，4，LIUXin-bao1，ZHAOLi-xin2，XIAJing-fan3，ZHANGLi2

(1. School of Management, Hefei University of Technology, Hefei 230009, China；2. School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China；3. Intelligent manufacturing institute, Hefei University of Technology, Hefei 230009, China;4. Committee for Discipline Inspection，Supervision Office，Hefei University of Technology Hefei 230009，China)

In order to recognize psychological crisis of college students effectively, according to the education statistics theory, a classification method based on dominance relation is used and a double limited dominance rough set approach and calculation method for early warning information system of psychological crisis of college students is established in this paper. According to the known properties values of each attribute of information system, the probability distribution is calculated. And the probability threshold is selected and compared with the obtained advantages of probability to realize the dominance relation judgment between each object. In addition, a comprehensive comparison and analysis of attribute reduction effect under different threshold probability is made to obtain the main factors of psychological crisis of college students.

According to the questionnaire survey and comparative analysis and calculation, it indicates that the obtained simplified results is more applicable, and has higher accuracy and a lower error rate of classification.

incompleteness; limited dominance relation; dominance probability; double limited dominance relation

1003-207(2017)11-0143-08

10.16381/j.cnki.issn1003-207x.2017.11.015

C931.2

A

2015-04-17；

2016-01-06

国家自然科学基金资助项目(71171071)

赵丽欣(1980-)，女(汉族)，河北藁城人，合肥工业大学电气与自动化工程学院，讲师，研究方向：教育教学、模式识别等，E-mail:55572651@qq.com.