剪叉式液压升降机结构的优化设计

摘 要：随着剪叉式液压升降机的广泛应用，本文主要对剪叉式液压升降机进行受力分析及力学模型的构建，通过设计分析得出液压缸的位置与举升力的关系，并采用软件ADAMS对其结构优化，得出最优解，具有实际效益及工程价值。

关键词：剪叉式；液压升降机；结构优化

DOI：10.16640/j.cnki.37-1222/t.2017.24.039

1 概述

随着社会经济的快速发展，一些高层建筑也相继拔地而起、基础设施的建设速度也在不断加快，这也使得高空作业设备需求量急速增加，而剪叉式液压升降机也受到广泛应用。顾名思义，剪叉式液压升降机的起升部分采用的是剪叉式、剪叉式机构是一种折叠机构、可收缩可展开，不使用时处于收缩状态、方便运输和储存；使用时处于展开状态、可缩短搭建时间，且该机构具有承载能力大、可操作范围广、安全系数高、工作稳定等特点，其应用范围较广泛、可应用于设备安装、路灯维修等高空作业。

2 剪叉式液压升降机结构的优化设计

剪叉式液压升降机主要由三个部分组成，即操作平台、起升机构和底座，，操作平台位于剪叉式液压升降机的最上部且四周装有护栏、为工作人员提供操作环境，承载能力大、保证工作人员的安全；起升结构位于整个升降机的中部、主要用于调节起升高度、其中的剪叉臂是整个升降机的核心部件之一、其内壁和外壁通过销轴相链接，可根据起升高度选择不同的剪叉臂架数目（有单剪叉式臂、双剪叉式臂、多剪叉式臂）；底座位于最底部。升降机内侧配置液压缸、为升降机的正常工作提供动力、且由于液压的作用保证升降机的稳定性，使其在断电或无动力的情况下、不会突然下落、也保障了工作人员的人身安全。根据移动方式不同分为固定式、牵引式及移动式剪叉式液压升降机，三者最大的区别是采用的底座结构形式不同，固定式升降机底座结构简单、只安装一副导轨和槽钢；牵引式升降机装有柴油机或驱动器等部件、靠柴油机或电力驱动；移动式升降机底座装有电瓶、控制器等部件；可根据运行成本及使用功能来选择不同的升降机。本文以固定式升降机进行受力分析及优化设计。

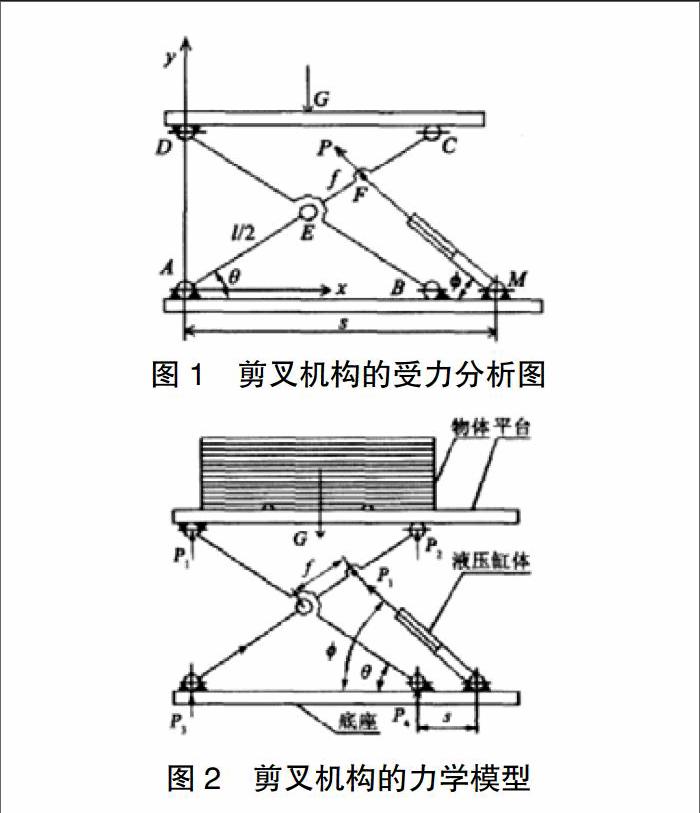
如图1所示，假定铰链约束是理想约束，根据虚伪移原理可得出公式1：

∑（Pxiδxi+ Pyiδyi+ Pziδzi）=0 （1）

由图1可得出公式2：

Pyδyp- Pxδxp- GδyG=0 （2）

且Px=Pcosφ，Py= Psinφ，xp=（L/2+f）cosθ， yp=（L/2+f）sinθ，

yG=Lsinθ，经运算、代入得出公式3：

（3）

由图2所示，选用相对称的两幅剪叉、液压缸布置在两幅剪叉之间、推动安装在一对剪叉臂的横梁上，根据几何关系可得公式4：

（4）

其中：P为液压缸活塞推力；G为台面荷重；L为剪叉杆长；s为安装点与滑块的距离；f为活塞推动横梁的安装点和剪叉中心孔的间距；θ为L与水平面的夹角；φ为液压缸与水平面的夹角；Pxi、Pyi、Pzi为作用在x、y、z轴上的主动力分量；δxi、δyi、δzi为作用在x、y、z轴上的虚位移分量。由公式3可以看出当台面荷重G不变时，P随着θ、φ的变化而变化，而θ、φ的大小由与结构尺寸存在一定关系；由公式4得出当s、f一定时，随着升降、φ隨着θ的变化而变化。

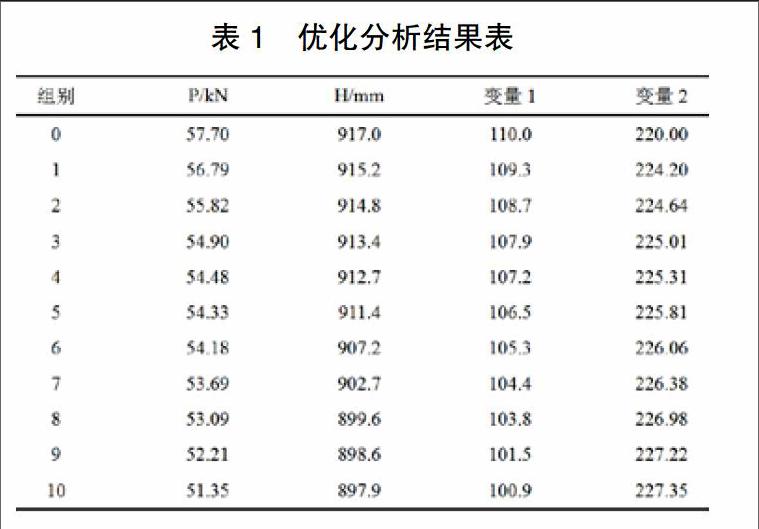
采用软件ADAMS对其进行结构优化，优化过程中、液压缸运行路径及速度不变、只改变支撑点的坐标值，其中设计变量1、2分别为液压缸安装点的纵坐标、横坐标，由几何关系确定参数的初值：f=200mm、s=220mm，最大举升力P=57.70kN，最大高度H=917mm（最大高度不低于900mm），优化见过如表1所示，在第八组数据时、最大高度无法满足最大高度要求、因此第七组数据为最优结果，根据相关数据，运用几何计算求得f=18.57、s=226.38。

3 结论

本文主要对剪叉式液压升降机进行受力分析及力学模型的构建，通过设计分析得出液压缸的位置与举升力的关系，并采用软件ADAMS对其结构优化，得出最优解，具有实际效益及工程价值。

参考文献：

[1]陈四华，周果，邓忠凯.剪叉式液压升降机的设计[J].机电设备，2015，32（S1）：7-10.

[2]石桐宁.剪叉式升降机构稳定性分析与结构优化[D].哈尔滨理工大学，2017.

作者简介：陈传燕（1987-），男，本科，助理工程师，从事设备管理与技术支持工作。