三油楔滑动轴承动力特性数值研究

孙 丹，韦纯浩，王 双，李胜远，艾延廷(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

航空宇航工程

三油楔滑动轴承动力特性数值研究

孙 丹，韦纯浩，王 双，李胜远，艾延廷
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

应用CFD动网格技术建立了三油楔滑动轴承动力特性求解模型。在验证求解模型准确性的基础上，研究了三油楔滑动轴承的流场特性，流体动压效应形成条件以及楔形度、偏心率、转速、偏位角、供油压力等因素对三油楔滑动轴承动力特性的影响。研究结果表明，随着偏心率的增加，三油楔滑动轴承的收敛楔形间隙逐渐变成发散楔形间隙，不再满足流体动压形成条件，使油膜正压区由3个逐渐变成1个。随着楔形度的增加，刚度系数和交叉阻尼系数变化不大，直接阻尼系数随之减小；随着偏心率的增大，刚度阻尼系数绝对值均随之增大；随着转速增大，直接刚度和阻尼系数变化较小，交叉刚度系数绝对值随之增大；随着偏位角的增大，直接刚度和交叉阻尼系数变化较小，交叉刚度与直接阻尼系数的绝对值均随之减小；供油压力对三油楔滑动轴承刚度阻尼系数影响较小，因此降低楔形度、转速、偏位角，增加偏心率将更有利于转子的稳定性。

三油楔滑动轴承；转子稳定性；动力特性；动网格

随着旋转机械向高参数方向发展，滑动轴承的动力特性系数是评价转子稳定性的重要参数。研究表明，相比于传统的圆轴承和椭圆轴承，三油楔滑动轴承在转子较大偏心下，仍然具有较好的动力特性，因此被广泛应用于汽轮机、燃气轮机等旋转机械[1-4]。

目前滑动轴承动力特性求解方法主要包括雷诺方程方法和CFD方法。早期国内外研究者大多利用雷诺方程的方法研究滑动轴承的动力特性[5-7]，由于雷诺方程是N-S方程的简化，忽略了惯性项、油膜曲率等重要因素，且当轴承形状和流体物性参数复杂时，其应用受到了限制。近年来，随着CFD技术的发展和计算机性能的提高，研究者逐渐通过CFD软件直接求解N-S方程的方法来研究滑动轴承的动力特性[8-9]。Guo等[10]应用CFD动网格方法建立了滑动轴承动力特性求解模型，研究了扰动位移与扰动速度对滑动轴承动力特性的影响;高庆水[11]、于桂昌[12]、熊万里[13]等人均建立了滑动轴承动力特性CFD求解模型。但上述文献均研究传统圆轴承的动力特性，张艾萍[14]研究表明，与圆轴承和椭圆轴承相比，三油楔滑动轴承不容易发生油膜震荡失稳故障，更有利于转子的稳定性，但现有文献对三油楔滑动轴承动力特性的研究较少，且未对其影响因素给予详细分析。

本文应用CFD动网格技术建立了三油楔滑动轴承动力特性求解模型，在验证求解模型准确性的基础上，研究了三油楔滑动轴承的流场特性，流体动压效应形成条件以及楔形度、偏心率、转速、偏位角、供油压力等因素对三油楔滑动轴承动力特性的影响。

1 基于动网格技术滑动轴承动力特性求解模型

1.1 三油楔滑动轴承动力特性理论求解模型

当转子在静平衡位置处受到微小扰动时，油膜力的变化量与动力特性系数和小扰动量近似成线性关系，其关系式为[15-16]

(1)

式(1)中，ΔFx，ΔFy为油膜力的变化量，Kxx，Kxy，Kyx，Kyy为刚度系数，Cxx，Cxy，Cyx，Cyy为阻尼系数，(x,y)为转子涡动位移，(x′,y′)为转子涡动速度。

由式(1)可得滑动轴承动力特性系数求解公式为

(2)

式(2)中，ΔFdij为位移扰动前后油膜力的变化量，ΔFvij为速度扰动前后油膜力的变化量。如图1所示，令转子在x方向产生小位移扰动量Δx，Δy、x′、y′均为0，根据位移扰动前后油膜力的变化量ΔFdxx和ΔFdyx，由式(2)便可求解滑动轴承刚度系数Kxx，Kyx。同理建立y方向的小位移扰动量Δy，便可求解刚度系数Kxy、Kyy。对于阻尼系数，需要使用CFD动网格技术，分别建立转子在x方向和y方向的小速度扰动量，根据速度扰动前后油膜力的变化量，求解滑动轴承阻尼系数。

图1 三油楔滑动轴承动力特性求解模型

1.2 三油楔滑动轴承动力特性数值求解模型

1.2.1 求解模型

三油楔滑动轴承的结构如图2所示。从图2中可以看出，三油楔滑动轴承具有几何中心O、转子中心O′以及油楔弧中心O1、O2、O3这3个重要位置。其中油楔弧中心与轴承几何中心O之间的预偏心距为d，油楔弧参考半径为R，转子半径为r，油膜半径间隙为c,预偏心距与轴承半径间隙之比为三油楔轴承楔形度γ。

3.3.2 追肥 应按照“适、巧、浅、匀”要求，依据树龄、树势和目标产量，于最需肥时期施入相应肥料，并搅拌均匀。

对于本文研究的三油楔滑动轴承，其轴承宽度L=25 mm，轴承参考半径R=25 mm，楔形度为γ=0.1,转子半径r=24.95 mm，3个油楔的最小油膜厚度分别为0.049 53 mm、0.050 09 mm和0.050 38 mm，转子偏位角ψ=49.8°，偏心率ε=0.01。

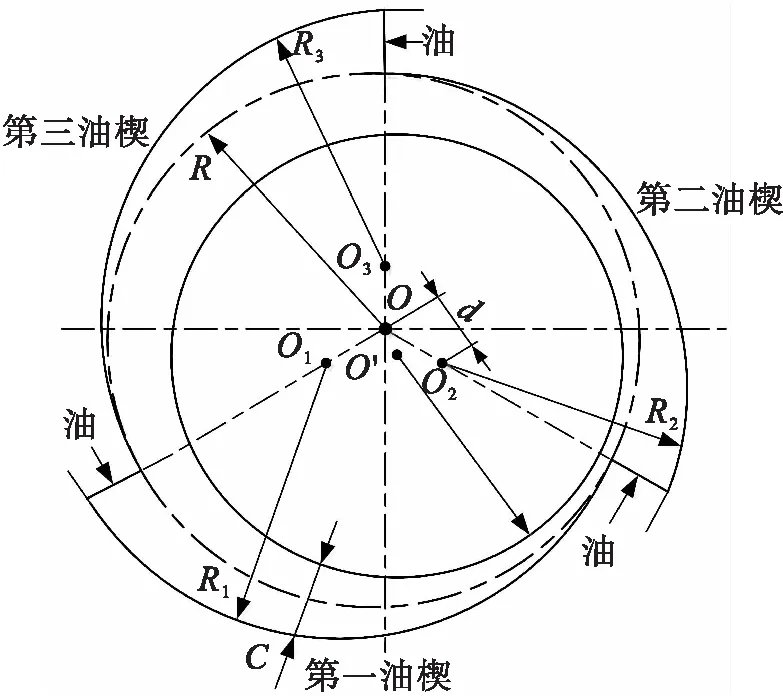
图2 三油楔滑动轴承结构示意图

1.2.2 网格划分

图3为三油楔滑动轴承网格图。本文采用结构化六面体网格以提高计算精度与节约计算时间。油膜间隙对计算结果影响较大，因此对油膜厚度方向加密处理，考虑到计算精度和计算时间等因素，经无关性验证后，三油楔滑动轴承的网格数最后确定为59.4万。

图3 三油楔滑动轴承网格图

1.2.3 边界条件

本文研究的三油楔滑动轴承的供油压力为103 kPa，转子转速为ω=9 550 r/min。润滑油密度ρ=876 kg/m3，动力粘度μ=0.0125 Ns/m2，润滑油的平均工作温度t=50 ℃。流体域流动状态为层流。固体壁面为固定无滑移边界，近壁面采用改进壁面函数法处理。

1.2.4 动网格技术

本文应用CFD软件求解N-S方程。求解滑动轴承阻尼系数时，为实现速度扰动，需要应用CFD动网格技术。CFD动网格技术主要是采用动边界文件(profile)方式，将转子表面设置一匀速运动边界条件，其时间步长取为0.001s，时间步数由偏移距离与扰动速度确定，每一时间步控制方程迭代残差均保证小于10-3。

1.2.5 求解模型准确性验证

文献[10]研究了圆轴承的动力特性并分析了其影响因素，该圆轴承宽25 mm，转子直径50 mm，偏心率为0.5，偏位角49.8°，轴承半径间隙为0.05 mm，油槽轴向长度3.75 mm，油槽周向角度为30°，润滑油密度876 kg/m3，供油压力103 kPa。为验证本文求解模型的准确性，将使用本文求解模型计算的该圆轴承的动力特性系数与文献[7]、[10]的计算结果相比，圆轴承的计算后果如表1所示，三者相对偏差如表2所示。其中文献[7]为应用Reynolds方程方法求解滑动轴承的动力特性系数，文献[10]应用CFD软件CFX-TASCflow软件求解层流模型的方法。由表2可以看出，本文求解模型的计算结果与文献[10]中CFX-TASCflow软件计算结果相差不大。与文献[7]中Reynolds方程方法相比，交叉项系数相差较大，这主要是由于两者求解方程不同引起的。

文献[7]中采用了雷诺方程方法研究滑动轴承的动力特性，由于雷诺方程是N-S方程的简化，忽略了惯性项、油膜曲率等重要因素，且当轴承形状和流体物性参数复杂时，其应用受到了限制。随着CFD技术的发展和计算机性能的提高，研究者逐渐通过CFD软件直接求解N-S方程的方法来研究滑动轴承的动力特性。本文采用的方法和文献[10]中CFX-TASCflow的方法均为CFD方法，其优点是直接求解三维未经简化的N-S方程，与传统雷诺方程相比求解精度较高，但其缺点是求解效率较低。

表1 圆滑动轴承刚度阻尼系数计算结果

表2 圆轴承计算结果与文献计算结果相对偏差比较

注：刚度系数比较以扰动位移x/h，y/h=0.005模型为例，阻尼系数比较以扰动速度模型为例。

2 三油楔滑动轴承流场特性分析

图4给出了不同偏心率下三油楔滑动轴承的油膜压力分布图。由于三油楔滑动轴承油膜不能承受较大负压，因此对油膜负压区应用Reynolds边界条件，对负压置零处理。由流体动压润滑理论可知，润滑油从进油口进入，顺着转子旋转方向，在由最大间隙到最小间隙的1/6圈内，间隙是由大变小的收敛楔形间隙，收敛楔形间隙为油膜能产生流体动压以承受外载的主要几何条件。而在由最小间隙到最大间隙的1/6圈内，为发散楔形间隙，在此区域内油膜压力急剧降低，油膜因不能承受负压而破裂。由图4中可以看出，三油楔滑动轴承在转子偏心率较小时，形成3个收敛楔形间隙，形成3个正压区。随着偏心率的增加，收敛楔形间隙逐渐变成发散楔形间隙，不再满足滑动轴承流体动压形成条件，油膜正压区逐渐由3个变成2个，最后变成1个。

图4 三油楔滑动轴承的压力分布特征

3 三油楔滑动轴承动力特性分析

3.1 楔形度对三油楔滑动轴滑动轴承动力特性影响分析

图5给出了不同楔形度对三油楔滑动轴承动力特性的影响。由图5可以看出，随着楔形度的增大，三油楔滑动轴承的刚度系数和交叉阻尼系数变化较小，直接阻尼系数随之减小，因此增加楔形度会降低转子的稳定性。

3.2 偏心率对三油楔滑动轴承动力特性影响分析

图6给出了不同偏心率对三油楔滑动轴承动力特性影响曲线。由图6可以看出，随着偏心率的增大，刚度系数与阻尼系数的绝对值均随之增大，因此增加偏心率可提高转子的稳定性。

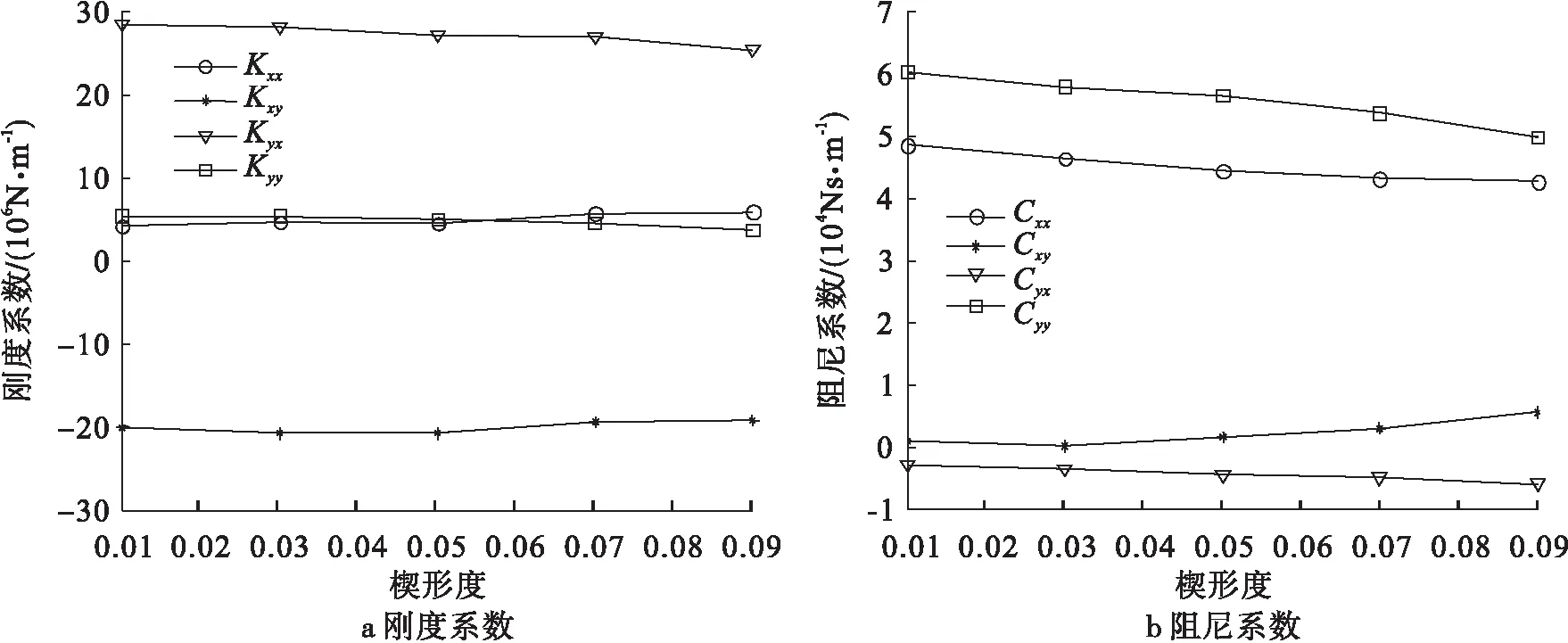
图5 楔形度对三油楔滑动轴承动力特性的影响

图6 偏心率对三油楔滑动轴承动力特性影响

3.3 转速对三油楔滑动轴承动力特性影响分析

图7给出了不同转速对三油楔滑动轴承动力特性影响曲线。从图7中可以看出，随着转速增大，三油楔滑动轴承的直接刚度和阻尼系数变化较小，交叉刚度系数绝对值随之增大，因此增加转速降低了转子的稳定性。

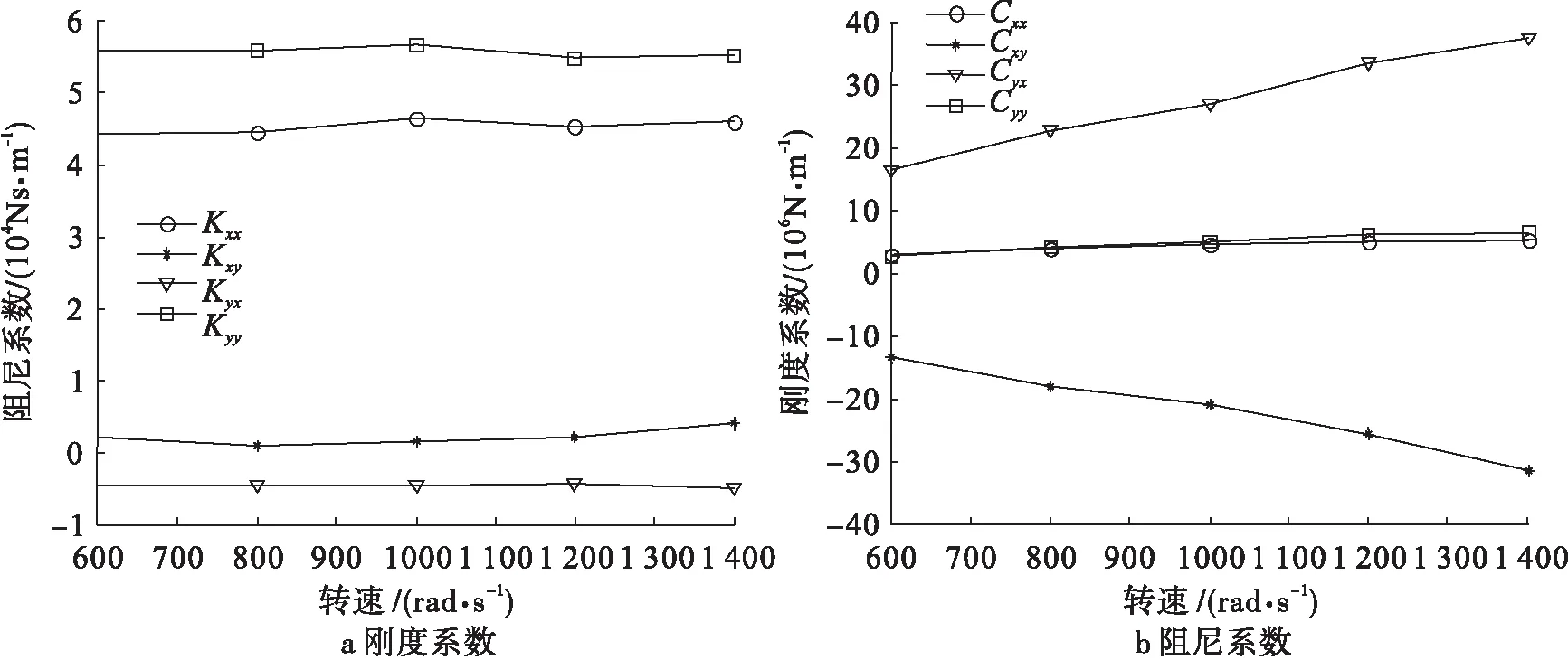
图7 转速对三油楔滑动轴承动力特性影响

3.4 偏位角对三油楔滑动轴承动力特性影响分析

图8给出了不同偏位角对三油楔滑动轴承动力特性影响。由图8可以看出，随着偏位角的增大，直接刚度和交叉阻尼系数变化较小，交叉刚度与直接阻尼系数的绝对值均随之减小，因此减小偏位角更有利于转子的稳定性。

图8 偏位角对三油楔滑动轴承动力特性影响

3.5 进油压力对三油楔滑动轴承动力特性影响分析

图9给出了不同压力对三油楔滑动轴承动力特性影响曲线。由图9可以看出，随着供油压力的增大，三油楔滑动轴承刚度和阻尼系数无明显变化，因此三油楔轴承的供油压力对转子稳定性影响较小。

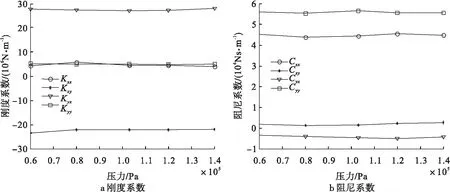
图9 进油压力对三油楔滑动轴承动力特性影响

4 结论

本文应用CFD动网格技术建立了三油楔滑动轴承动力特性求解模型。在验证求解模型准确性的基础上，研究了三油楔滑动轴承流场特性，流体动压效应形成条件以及楔形度、偏心率、转速、偏位角、供油压力等因素对三油楔滑动轴承动力特性的影响，得出以下结论：

(1) 随着偏心率的增加，三油楔滑动轴承中的收敛楔形间隙逐渐变成发散楔形间隙，不满足流体动压形成条件，使正压区从原来的3个逐渐变成了1个。

(2)随着楔形度的增加，刚度系数和交叉阻尼系数变化不大，直接阻尼系数随之减小；随着偏心率的增大,滑动轴承动力特性系数绝对值均随之增大；随着转速增大，直接刚度和阻尼系数变化较小，交叉刚度系数绝对值随之增大；随着偏位角的增大，直接刚度和交叉阻尼系数变化较小，交叉刚度与直接阻尼的绝对值均随之减小；供油压力对三油楔滑动轴承刚度阻尼系数影响较小。

(3) 降低楔形度、转速、偏位角，增加偏心率将更有利于转子的稳定性，供油压力对转子稳定性影响较小。

[1] 钱坤.速度对三油楔滑动轴承轴心位置及摩擦力的影响[J].轴承,2008(6):5-7.

[2] 钱坤,李兴林.三油楔滑动轴承润滑模拟及平衡位置求解[J].润滑与密封,2008,33(10):52-54.

[3] 钱坤.三油楔滑动轴承轴心位置及摩擦力和承载能力的影响参数分析[J].机床与液压,2008,36(10):232-234.

[4] 张艾萍,谢媚娜,林圣强.基于两相流三油楔滑动轴承的油膜特性分析[J].润滑与密封,2015(9):47-52.

[5] 杨建刚，郭瑞，高亹.基于径向基函数的滑动轴承压力分布求解模型[J].中国电机工程学报，2005，25(6)：157-158.

[6] ALMQVIST T,ALMQVIST A,LARSSON R.A comparison between computational fluid dynamic and Reynolds approaches for simulating transient EHL line contacts[J].Tribology International,2004,37(1):61-69.

[7] 孙丹,杨建刚,郭瑞.基于局部微分求积-拉格朗日法的滑动轴承动力特性求解模型[J].中国电机工程学报,2011,31(14):90-95.

[8] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京：清华大学出版社,2004.

[9] 岑少起.计入能量和状态方程时有限长滑动轴承的完全Navier-Stokes解[J].机械工程学报,1995(2):51-56.

[10]GUO,ZENGLIN,HIRANO,et al.Application of CFD Analysis for Rotating Machinery-Part I:Hydrodynamic,Hydrostatic Bearings and Squeeze Film Damper[J].Journal of Engineering for Gas Turbines & Power,2005,127(2):445-451.

[11]高庆水,杨建刚.基于CFD方法的液体动压滑动轴承动特性研究[J].润滑与密封,2008,33(9)：65-67.

[12]于桂昌,刘淑莲,郑水英.基于CFD的滑动轴承动力特性的数值计算方法[C]// 全国设备故障诊断学术会议，2010.

[13]熊万里,侯志泉,吕浪,等.基于动网格模型的液体动静压轴承刚度阻尼计算方法[J].机械工程学报,2012,48(23):118-126.

[14]张艾萍,林圣强,谢媚娜.三油楔滑动轴承油膜压力特性及对转子稳定性的影响[J].动力工程学报,2013,33(6):437-442.

[15]CHILDS D.The remarkable turbomachinery-rotordynamics developments during the last quarter of the 20th century[R].SAE Technical Paper,2015.

[16]DAWSON M P,CHILDS D W.Measurements versus predictions for the dynamic impedance of annular gas seals:part 2-smooth and honeycomb geometries[C]//ASME Turbo Expo 2001:Power for Land,Sea,and Air.American Society of Mechanical Engineers,2001:V004T03A006-V004T03A006.

Numericalstudyondynamiccharacteristicsofthree-lobejournalbearing

SUN Dan,WEI Chun-hao,WANG Shuang,LI Sheng-yuan,AI Yan-ting
(Liaoning Key Laboratory of Advanced Measurement and Test Technology of Aviation Propulsion System,Shenyang Aerospace University,Shenyang 110136,China)

A solving model of the dynamic characteristics of three-lobe journal bearings was established by CFD technology.After the accuracy was verified,the model was used to investigate the flow characteristics of three-lobe journal bearings,the formation of hydrodynamic action and effects of wedge degree,eccentricity,inlet pressure,and rotational speed.The results show that with the increase of eccentricity,gaps of the lobes get big gradually,which cannot form hydrodynamic action and make the three positive pressure areas of oil film become one area.Stiffness coefficient and cross damping coefficient remain relatively unchanged,while direct damping coefficient decreases with the increase of wedge degree.Absolute values of stiffness and damping coefficients increase as the eccentricity ratio increases.With increasing rotational speed direct stiffness and damping coefficients have no obvious change,but absolute value of cross stiffness increases.Both cross stiffness and direct stiffness change slightly,and their absolute values decrease as attitude angle increases.Oil supply pressure has a minor effect on stiffness and damping coefficients.Therefore,the decrease of wedge degree,rotational speed and attitude angle and the increase of eccentricity are good for stability of the rotor.

three-lobe journal bearing;rotor stability;dynamic characteristics;dynamic mesh

2017-05-17

国家自然科学基金(项目编号：51675351)

孙 丹(1981-)，男，辽宁丹东人，副教授，博士，主要研究方向：透平机械滑动轴承与密封动力特性，E-mail:phd_sundan@163.com。

2095-1248(2017)06-0009-07

TH133.31；O242.21

A

10.3969/j.issn.2095-1248.2017.06.002

吴萍 英文审校：赵欢)