截距同号且存在一个排斥不动点的分段线性映射的动力学分析
2017-12-26顾恩国罗阿木卢俊波
顾恩国,罗阿木,卢俊波
(中南民族大学 数学与统计学学院,武汉 430074)
截距同号且存在一个排斥不动点的
分段线性映射的动力学分析
顾恩国,罗阿木*,卢俊波
(中南民族大学 数学与统计学学院,武汉 430074)
为补充和完善前人对分段线性映射动力学行为的研究,首先,对参数进行了初步的分类;然后分别分析每一种情况下系统的动力学行为,探讨了BCB分叉、flip分叉、接触分叉以及混沌等现象,并研究了共存吸引子、吸引域的定界和分叉;最后,结合数值模拟对理论结果进行了验证.
分段线性映射;BCB分叉;flip分叉;接触分叉;混沌
分段线性映射模型在电子电路模型、非线性振子模型、基因组序列模型等方面有着直接应用,也在工程和物理学[1-3]、电子和机械[4,5]、社会科学、经济学、生物学[6]等方面有着广泛应用.所以很多学者开始重视分段线性映射的研究[1-6].
本文研究的不连续分段线性映射系统为:
(1)
该映射中含有4个参数aL,aR,μL,μR,原点0是唯一不连续点,对于有其他不连续点的情况也可通过坐标变换将不连续点变换为原点进行分析.文献[7]研究了映射在0
分叉现象在动力系统的研究中具有重要意义,它使得系统动力学行为随参数变化,本文将研究不连续的分段线性映射系统(1)的BCB分叉(由不变集和映射系统定义的边界发生碰撞产生)、flip分叉、接触分叉,并给出BCB曲线,BCB曲线最先由Leonov于1959年提出,文献[10]、[11]中也给出了详细的阐述.
在本文中,首先对所要研究分段线性映射的一般性质进行简要分析,然后分两种情况计算了BCB曲线,给出了flip分叉、共存吸引子和混沌吸引子的存在条件,并对有界吸引子进行定界,最后分析了混沌产生的条件.
1 分段线性映射的一般性质
考虑的分段线性映射族为(1)式,4个参数满足约束条件:
aL≥1,aR<0,μLμR>0.
(2)
该线性映射g(x)满足镜面对称性:
g(x,aL,aR,μL,μR)=-g(-x,aL,aR,-μL,-μR).
本文仅讨论左边不动点为排斥的且截距为正即μL,R>0的情况,右边不动点为排斥的且截距为负的情况可由对称性得到.
若aL>1,aR<0,μL,R>0,那么该线性映射具有两个不动点在Y轴的两侧分别为:
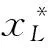
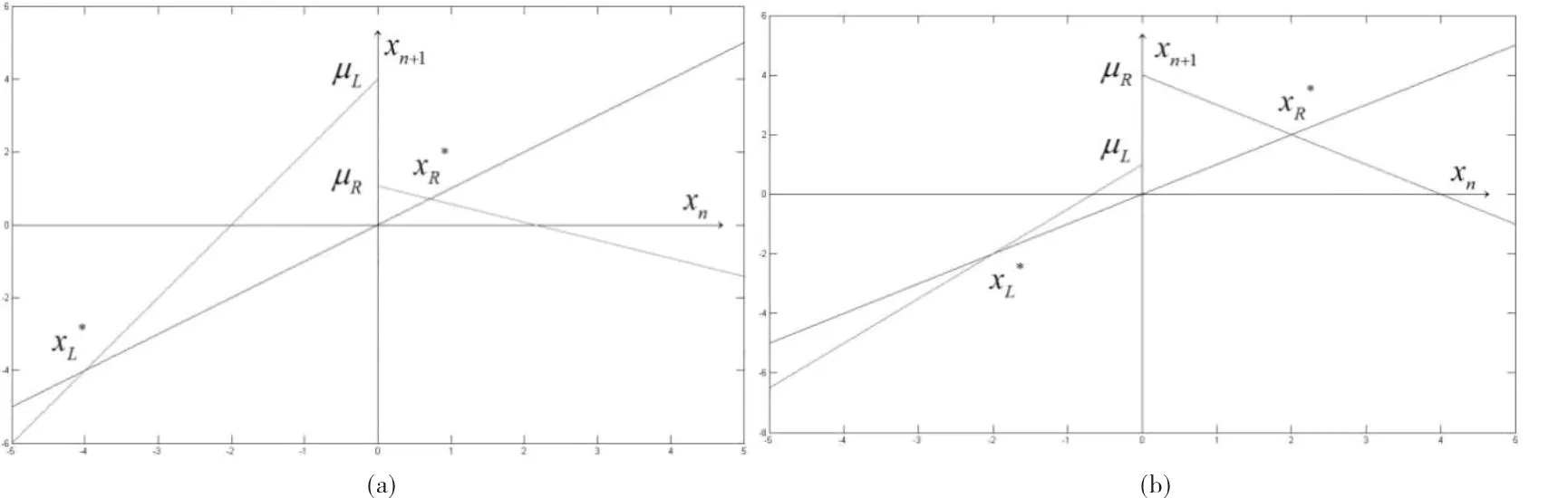
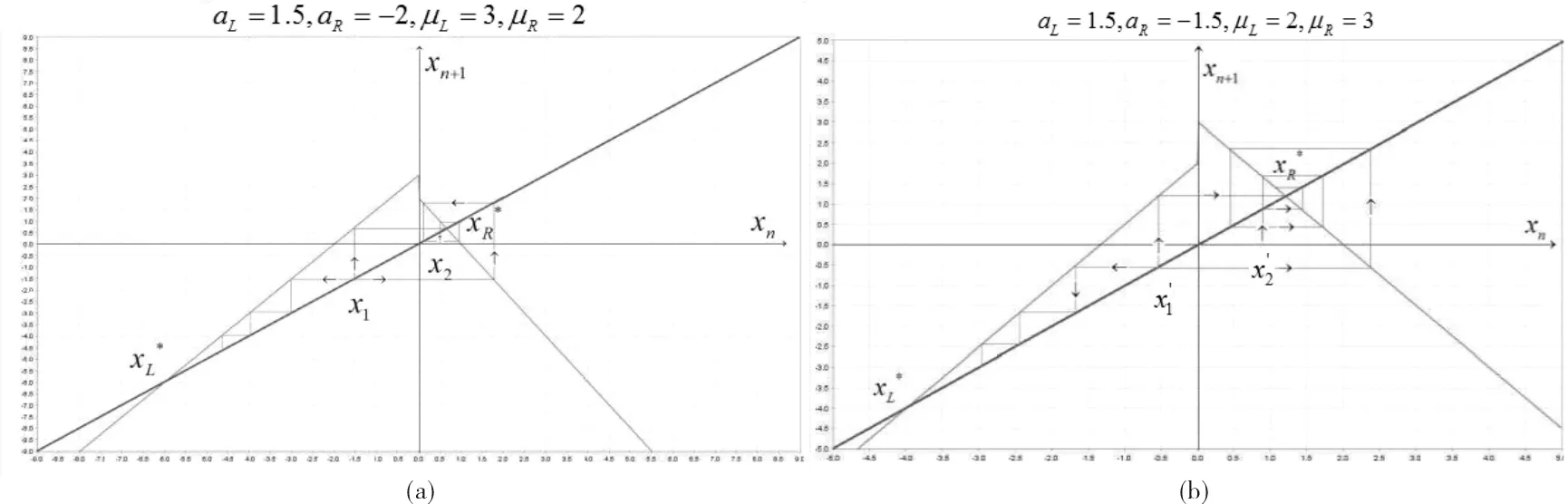
图1 分段线性映射图Fig.1 Diagram of piecewise linear map
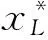
2 分段线性映射的动力学行为
2.1 aL=1,aR=-1条件下的动力学行为
当aL=1,aR=-1时,映射变为:
命题1 假设aL=1,aR=-1,则映射满足:
(a) 若μL<μR,吸收区间I=[0,μR]中除中点外任意点均为二周期点,I的吸引域为(-∞,+∞);
(b) 若μL>μR,吸收区间D=[-μL+μR,μL]中有两类吸引子,在I中除中点外任意点均为二周期点,在DI=[-μL+μR,0)∪(μR,μL]中除[-μL+μR,0)及(μR,μL]的中点外任意点均为四周期点,D的吸引域为(-∞,+∞).
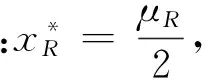
不妨令∀x0∈[-μL+μR,0],由:
x1=gL(x0)=x0+μL,
x2=gR∘gL(x0)=-x0-μL+μR,
x3=gL∘gR∘gL(x0)=-x0-μL+μR+μL=
-x0+μR,
x0=gR∘gL∘gR∘gL(x0)=x0-μR+μR=x0,
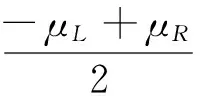
图2(a)给出了假四周期轨即二周期轨的情况,如图2(b)给出了任意一种四周期轨的情况.取参数0<μL,μR<4作出二维分叉图,如图3,次对角线下方即μL<μR时只有二周期轨,与上述分析一致.在次对角线上方即μL>μR时,从图中可以看出,映射系统仅有二、四周期的周期轨.根据以上分析可知,所取的初始点x0=-2可能在吸收区间D之外,所以当-μL+μR<-2+kμL<0,k∈N*时有四周期轨存在,因此二周期轨向四周期轨过渡的BCB曲线为:-μL+μR=-2+kμL,四周期轨向二周期轨过渡的BCB曲线为:-2+kμL=0,由该解析式可知BCB曲线是水平的较为简单,故而在图中不作注明.取k=1,2,3,4作出部分BCB曲线如图4,再与图3对比可知刚好是灰色和浅灰色两种不同颜色区域的边界.
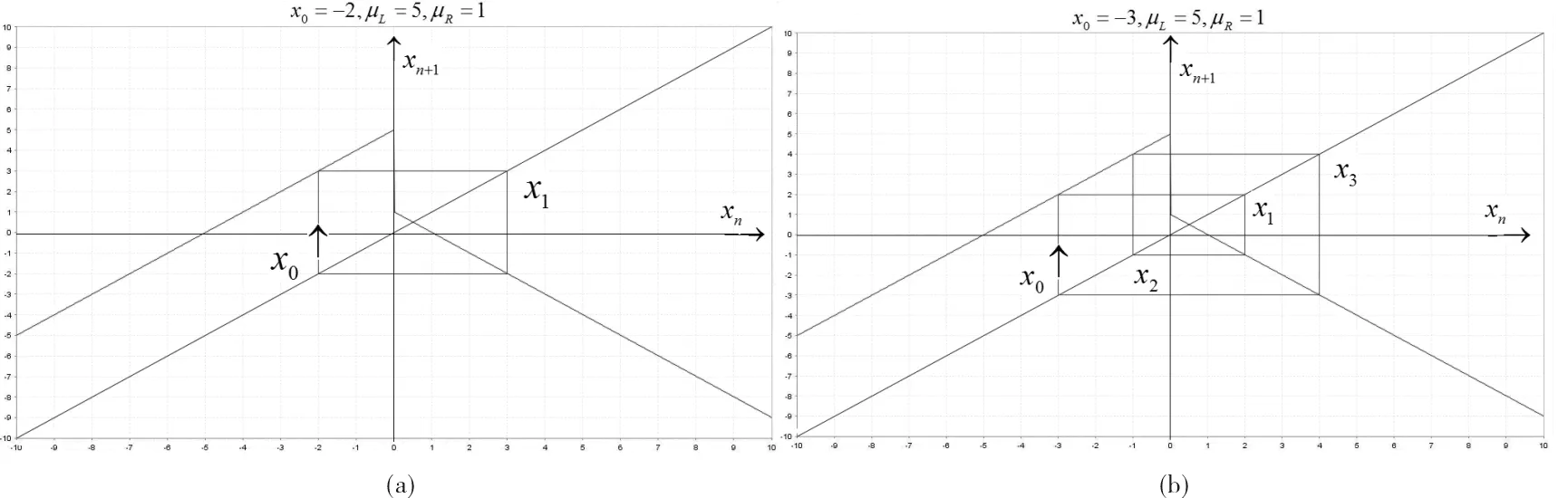
图2 二周期和四周期轨线图Fig.2 Diagram of two cycle and four cycle trajectory
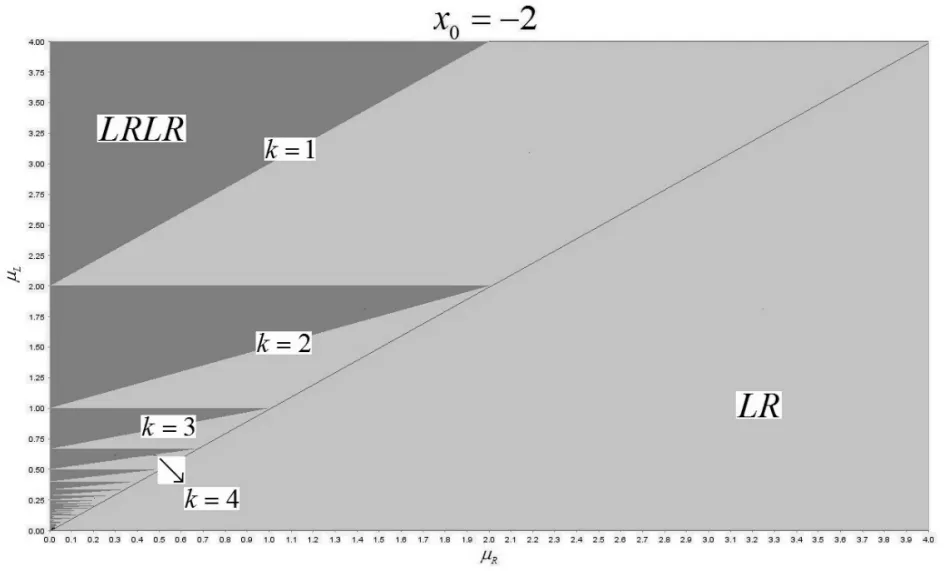
图3 二维分叉图Fig.3 Diagram of two-dimensional bifurcation
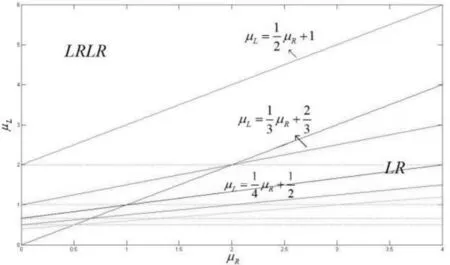
图4 BCB曲线Fig.4 BCB curve
2.2 aL>1,aR<0条件下的动力学行为
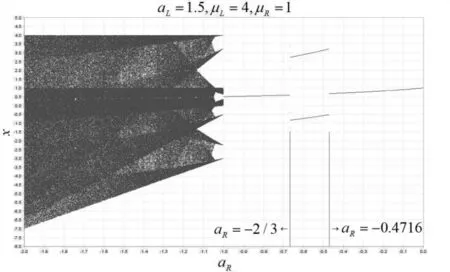
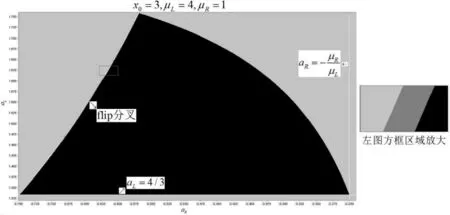
2.2.1aL>1,-1 图5 一维分叉图 Fig.5 Diagram of one-dimensional bifurcation 图6 二维分叉图Fig.6 Diagram of two-dimensional bifurcation 图6二维分叉图给出了形成稳定二周期轨的边界条件,对于该吸引的二周期轨,记作:O(2)={x0,x1},aRμL+μR 图7 共存吸引子吸引域Fig.7 Basin of attraction for coexistence attractors 以下通过数值模拟对以上分析进行验证,取aR=-0.6,可计算出一个稳定二周期轨为:O(2)={-0.74413866,2.8848114},恰为图7中闭合的矩形. I0=(0,5/8),I1=(-8/3,-9/4), O{4}={-1.2538227,2.1100917,-0.41794088,3.374108}. 图8 无穷吸引子吸引域图 Fig.8 Diagram for basin of infinite attractor 图9 二维分叉图Fig.9 Diagram of two-dimensional bifurcation 当-1 综上所述,我们得到如下命题2. 命题2 假设aL>1,-1 (b) 当μL=μR时,映射化为分段光滑的帐篷映射; 2.2.2aL>1,aR<-1条件下的动力学行为 图10 同宿轨线图 Fig.10 Diagram of homoclinic trajectory 当μL=μR时,为μL<μR和μL>μR情况的临界过渡,此时映射化为分段光滑的帐篷映射. 命题3 假设aL>1,aR<-1,则映射系统不可能存在周期吸引子. (b) 当μL=μR时,映射化为分段光滑的帐篷映射; 本文对有一个不连续点的分段线性映射系统(1)在aL≥1,aR<0,μLμR>0条件下的动力学行为进行了分析.当aL=1,aR=-1时系统只存在二、四周期的周期轨,求出了从二周期向四周期过渡,四周期向二周期过渡的BCB曲线;当aL>1,-1 [1] Banerjee S, Karthik M S, Yuan G H, et al. Bifurcations in one-dimensional piecewise smooth maps theory and applications in switching circuits [J]. IEEE T Circuits-I, 2000, 47(3): 389-394. [2] Banerjee S, Verghese G C. Nonlinear phenomena in power electronics:attractors, bifurcations, chaos and nonlinear control [M]. New York: IEEE Press, 2001: 34-82. [3] Dankowicz H, Nordmark A B. On the oriin and bifurcations of stick-skip oscillations [J]. Physical Review D, 2000, 136: 208-302. [4] Puu T, Sushko I. Oligopoly dynamics, models and tools [M]. New York:Springer-Verlag, 2002: 86-122. [5] Puu T, Sushko I. Business cycle dynamics, models and tools [M]. New York:Springer-Verlag, 2006: 117-136. [6] Coutinho R, Frenandez B, Lima R, et al. Discrete time piecewise affine models of genetic regulatory networks [J]. Mathematical Biology, 2006, 52: 524-570. [7] Gardini L, Tramontana F. Border collision bifurcation curves and their classification in a family of 1D discontinuous maps [J]. Chaos,Solitons & Fractals, 2011, 44(4): 248-259. [8] Gardini L, Tramontana F. Border-collision bifurcations in 1D piecewise-linear maps and Leonov′s approach[J]. International Journal of Bifurcation and Chaos, 2010, 20(10): 3085-3104. [9] Gardini L, Tramontana F. Border collision bifurcations in 1D PWL map with one discontinuity use of the first return map [J]. International Journal of Bifurcation and Chaos, 2010, 20(11): 3259-3574. [10] Nusse H E, Yorke J A. Border-collision bifurcation for piece-wise smooth one-dimensional maps [J]. International Journal of Bifurcation and Chaos, 1995, 5: 189-207. [11] Nusse H E, Ott E, Yorke J A. Border-collision bifurcations:an explanation for observed bifurcation phenomena [J]. Physical Review E, 1994, 49(107): 3-6. [12] 顾恩国. 离散动力系统的分叉和混沌[M]. 北京:科学出版社,2013: 17-19. [13] 顾恩国,鲁嘉珺. 环境污染与自然资源耦合系统的动力学模型分析[J]. 中南民族大学学报(自然科学版),2017,36(3):142-146. DynamicalAnalysisofPiecewiseLinearMapswiththeSameInterceptSignandOneRepulsiveFixedPoint GuEnguo,LuoAmu,LuJunbo (College of Mathematics and Statistics, South-Central University for Nationalities,Wuhan 430074,China) In this paper, the study on the dynamic behavior of piecewise linear map was complemented and perfected. Firstly, a preliminary classification of the parameters is given. Then dynamical behavior of each case was analyzed. BCB bifurcation, flip bifurcation, contact bifurcation and chaos phenomenon, coexistence attractors, basin delimitation and bifurcation of attractors were presented. At last, numerical simulation was used to verify the theoretical results. piecewise linear map;BCB bifurcation;flip bifurcation;contact bifurcation;chaos 2017-04-06 * 罗阿木,研究方向:非线性动力学应用,E-mail:1194846493@qq.com 顾恩国(1964-),男,教授,研究方向:非线性动力学应用,E-mail:guenguo@163.com 国家自然科学基金资助项目(61374085) O193 A 1672-4321(2017)04-0131-06
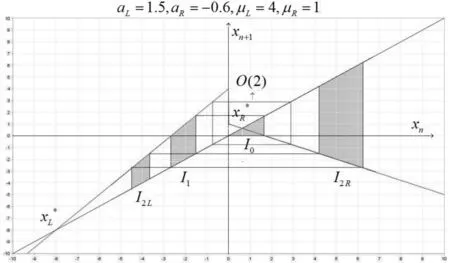
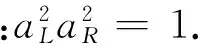
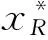
I2L=(-40/9,-25/8),I2R=(65/12,55/9).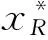
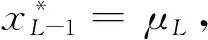
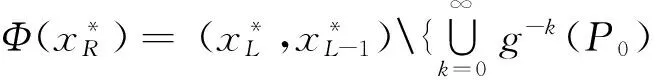
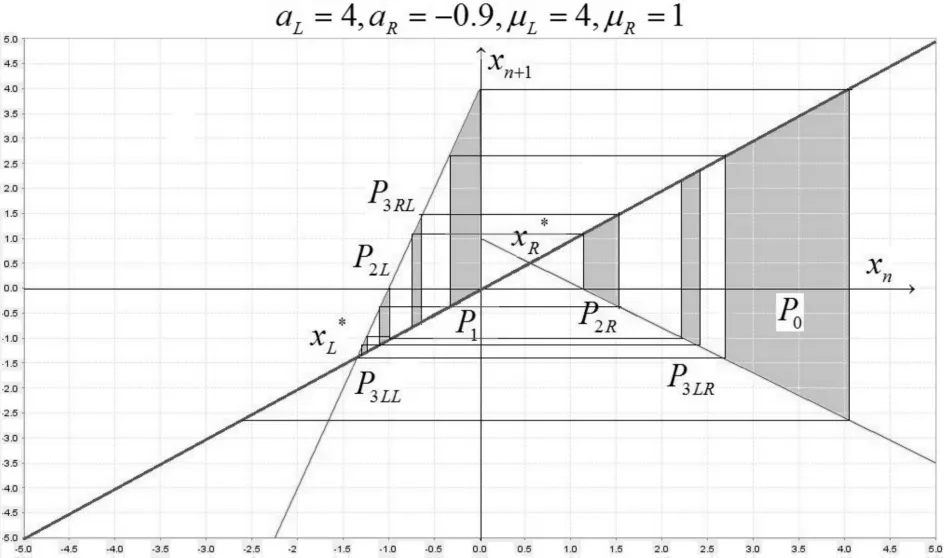
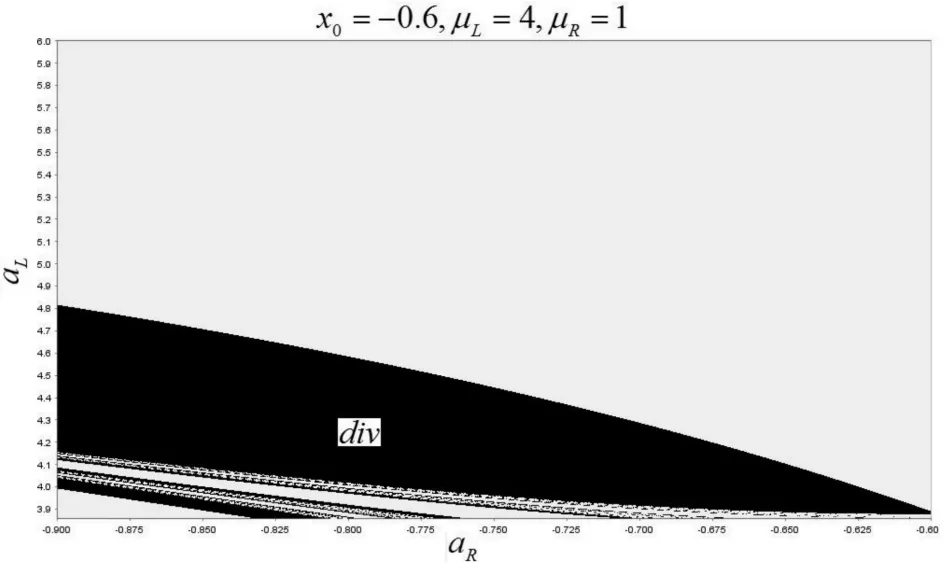
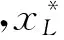
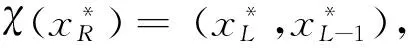

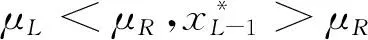
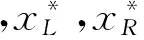
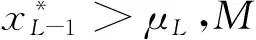
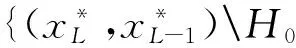
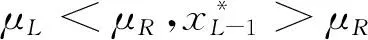

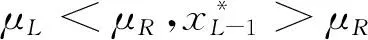
3 小结
