非线性随机网络编码研究

张东秋

(牡丹江师范学院 计算机与信息技术学院，牡丹江157011)

非线性随机网络编码研究

张东秋

(牡丹江师范学院 计算机与信息技术学院，牡丹江157011)

针对网络编码里的“全有或全无”以及因线性网络编码纠错能力过低而导致重传代价过大的问题，提出了非线性随机网络编码的方法.该法用有限域上非线性函数的系数代替线性网络编码里的线性函数系数，在中间节点用一般的非线性函数对上游消息进行复合函数操作，在信宿节点用查表法进行译码.实验结果表明：非线性随机网络编码比线性网络编码具有更低的能量消耗、更低的时延，码的长度相同时能纠正更多的错误.

网络编码；非线性；纠错

网络编码技术可以增强多播网络的吞吐量，具有巨大的应用前景[1].目前网络编码主要采用线性编码方案[2],线性网络编码主要采用有限域上的线性函数进行运算.在线性随机网络编码中，每个数据包的头部都携带一个编码向量，该向量为待解n维消息向量的系数向量[3].假若中间节点从K条入边收到K个消息，对于其每一条出边，会在本地随机产生一个K维的有限域上的向量，利用该向量与收到的消息包相乘，然后将得到新的数据包在该条出边上发送出去,中间节点对每一条出边都从事上述操作.信宿节点如果收到含n个消息的头部编码向量组成的矩阵满秩，利用线性方程理论就可以解码出原始消息.

线性网络编码方案具有实现方案简单、计算复杂度低等特点.李硕彦证明了针对多播网络，线性网络编码可以达到多播容量上限[1].但线性网络编码依然具有几个明显缺点.首先，在非多播即一般网络里，勒曼已经证明线性网络编码并不能达到所有类型非多播网络的容量上限[4].其次，线性网络编码存在“全有或全无”问题[5]，当随机线性网络编码里的编码向量彼此不独立时，无法得出唯一解，造成解码失败.此时，即使想恢复信源消息的一小部分也不可能[5, 6].第三，即使是在多播网络里，虽然线性网络编码可以达到多播容量上限，但必须有一个前提条件是网络不存在错误，如果有错误发生，因为中继节点对上游消息的多次组合操作，所以即使很小的错误也有可能扩散至全网而造成信宿节点不可译码[7].

针对线性网络编码的上述问题，提出非线性网络编码的概念[8].非线性网络编码和线性网络编码的本质区别是其采用非线性函数来代替线性函数.针对n个原始消息，编码包头部的编码向量不再是n维的，而是qn维的，它代表有限域Fq上的每个变量最高为q-1次的多项式的系数.非线性网络编码可以部分地克服线性网络编码的上述缺点.

1 随机线性网络编码

1.1 线性网络编码模型

设G(V,E)是无延迟的通信网络.信源节点集：{s1,s2,…}⊂V，信宿节点集：R={r1,r2,…}⊂V，边e的头节点用h(e)=v表示，边e的尾节点用t(e)=v′表示.X(v,i)表示源节点v的n长消息的第i个字符.称这样的编码为线性网络编码，如果对于网络中的每一条边e=(v,v′)的传输符号均满足：

(1)

其中αi,e,βe′,e∈Fq.

从函数映射角度，对边集E中的每条边e=(v,v′)，存在一种映射：

(2)

这里，fg是有限域Fq上的线性函数.本文主要考虑一个信源节点的多播网络，此多播网络最大流最小割为n，所以信源消息是一个n长的一维向量.

随机线性网络编码模型如图1所示. 源节点v发出的的原始待解消息数据包X(v,i)用Xi表示.节点从入边收到的包个数为K.如果是信宿节点，由于最大流最小割是n，其最大有效数据包个数为n，即K=n.信宿收到n个数据包为Y1,…，Yi,…，Yn.Yi头部包含一个n长的编码向量gi,1,gi,2,…,gi,n.收到的n个数据包Y=(Y1,Y2,…,Yn)为一组，针对的待解信源消息为X=(X1,X2,…,Xn).

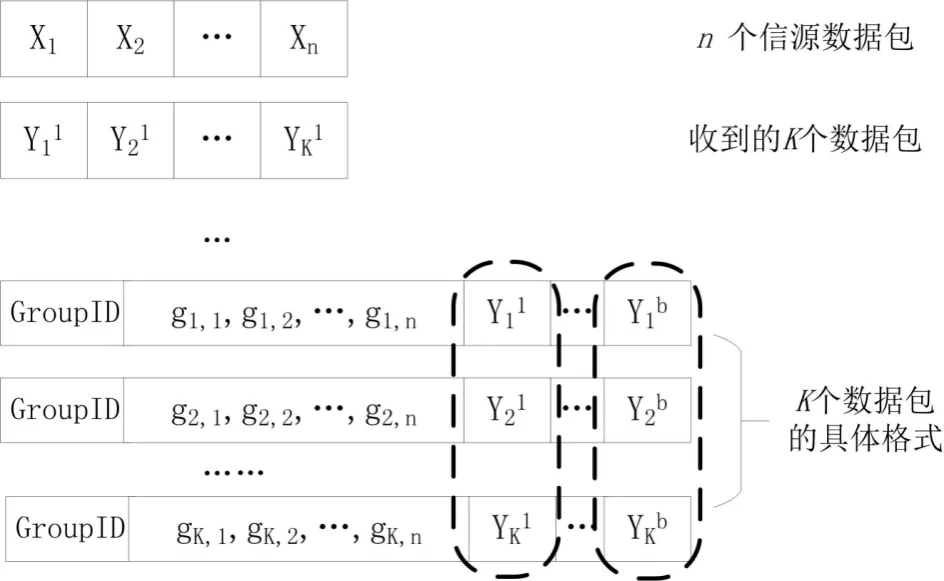
图1 随机线性网络编码成组传输数据包格式Fig.1 The data-packet format of group transmission in random network coding

网络中存在很多这样的组，为了区别哪些数据包为一组，用数据包的头部数据区Groupid进行唯一标识.为了节省头部编码向量标标识带来的通信开销，这里进行成组传输，每组容纳的Y1,…,Yi,…,Yn个数为b，b越大，数据包的头部数据区Groupid带来的开销将被稀释得越厉害[9].

1.2 线性网络编码的不足

第一是线性网络编码不能达到所有类型非多播网络的容量上限.勒曼指出，针对某些非多播网络，非线性网络编码能带来更多的传输增益[4].

第二是解码时存在“全有或全无”问题.由图1可知，信宿节点解码时会将n个编码向量组合在一起形成一个关于未知数X1,…,Xi,…,Xn的n元一次线性方程组.方程组的系数矩阵记为：

(3)

方程记为：GX=Y.如果G满秩，则能解出信源消息X，但如果G不满秩，则不能得到X的任何一部分.上述问题是线性网络编码里的“全有或全无”问题.一般的解决方法是重传更多的数据包直到G满秩.但这样会加重传输负担，降低传输效率.

第三是线性网络编码的纠错能力不强.网络编码中的错误和点对点通信中的错误不同，由于中间节点的混合操作，原始发生的错误会不断被扩散至下游节点而造成信宿节点不可译码.

2 非线性随机网络编码

2.1 非线性随机网络编码模型

如果将(2)式的函数fg调整为有限域Fq上的非线性函数，那么线性网络编码将成为非线性网络编码.

2.1.1 非线性编码向量

其数据包格式和图1基本相同.不同的主要是编码向量由gi,1,gi,2,…,gi,n改为gi,q1,gi,q2,…,gi,qn，也就是编码向量长度由n变为qn.为了减小消息包头部编码向量的开销，有限域设定为{0,1}，即q=2.虽然非线性编码向量的长度比线性编码的长度大很多，但是如果不断加大图1中成组传输里的b的数值，由此带来的通信开销会不断减小.

2.1.2 中间节点的非线性编码复合函数

若中间节点从K条入边收到K个消息，对于其每一条出边，会在本地随机产生一个K元多项式函数fe，可以看作是有限域Fq上的的每个元的最高次幂为q-1的多项式.因为Fq={0,1}，所以每个元最高次幂为1，则该函数有2K个系数.其通式如下：

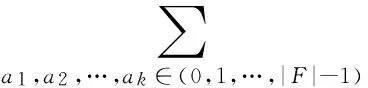
(4)

当某一中间节点收到3个消息时，即K=3，则:

fe=x1+x1x2x3+x2+x2x3+x1x3，

(5)

系数c(a1,a2,…,aK)从有限域Fq上随机选取.K个数据包头部的编码向量实际上对应以原始n个数据包X1,…，Xi,…Xn，为变量的有限域Fq上的多项式，用gi(X1,…，Xi,…，Xn)(1≤i≤K)表示该多项式函数.针对出边e，节点的局部编码函数不再是线性编码里的公式(1)，而是复合函数操作，即

f(g1(X1,…，Xi,…，Xn),…,gk(X1,…，Xi,…，Xn))=

fg(X1,…，Xi,…，Xn)=

(6)

复合函数操作之后函数的多项式系数组成新的数据包，然后发送到出边e上.该数据包头部的编码向量即为λ1,λ2,…，λn，它与图1中λ的gi,1,gi,2,…,gi,n是同一个具体值，即(λ1,λ2,…，λn)=(gi,1,gi,2,…,gi,n).非线性复合函数的运算过程可以用图2表示.

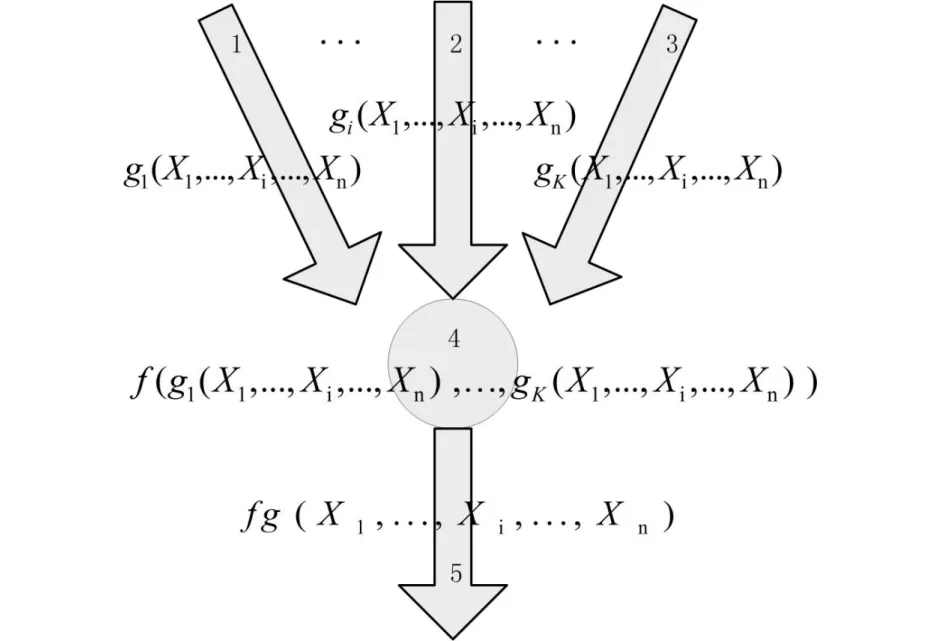
图2 中间节点的非线性编码复合函数Fig.2 The composite function of an intermediate node for non-linear coding

图2中，有三条入边，一条出边以及一个中间节点.三条入边本身被赋予相应的全局编码函数，中间节点具有一个局部函数.这三个全局编码函数在经过中间节点局部编码函数的复合之后形成新的全局编码函数，然后将这个新的全局编码函数赋予出边.这样就完成了中间节点的非线性网络编码操作.

2.1.3 无错误时的信宿节点的译码

不像线性网络编码的译码，非线性编码里信宿节点通过查表法进行译码.信宿节点会在本地产生n个随机多项式函数，每个随机多项式对入边的消息进行复合函数运算，得出一个编码包，然后传到信宿节点中的一条想象出边上.因为有n个原始消息，所以对应有n条想象出边.假设计算出来的n条想象出边上的数据包头部编码向量对应的多项式函数为f1(X1,X2，…，Xn),…，fn(X1,X2，…，Xn)记为f1,…,fn.根据这些编码向量绘制解码函数数值对应表，如表1所示.

表1 解码函数Tab.1 The decoding function

当(a1,…,an)，(b1,…,bn)，(c1,…,cn)为(X1,…,Xn)的值确定时，(f1,…,fn)的具体取值也确定.信宿节点的n条想象出边上收到的n个数据包的数值部分，即图1中的Y=(Y1,…,Yi,…，Yn)也对应(f1,…,fn)的一组具体值，其为(f1,…,fn)=(Y1,…,Yi,…，Yn).在表1中找到(Y1,…,Yi,…，Yn)，其对应的(X1,…,Xn)即为原始信源消息.

上述译码成功的前提是表1确定的映射关系是一一映射.假设针对(Y1,…,Yi,…，Yn)有两组或以上的(X1,…，Xn)与之对应组合，则译码失败.

2.2 非线性随机网络编码的优势

2.2.1 解决全有或全无问题

如果是线性编码，当G不满秩时，GX-Y总是得不到解.当n=3时，表2和表3是线性编码和非线性编码时译码函数不是完全一一映射函数时的各自的一个具体例子.可以发现，线性编码时，针对每一个(f1,…,fn)组合，总有两个具体的(X1,…,Xn)组合与其对应.非线性编码时，虽然对某些(f1,…,fn)组合，总有多个的具体(X1,…,Xn)组合与其对应，但还有很多(fn,…,fn)和(X1,…,Xn)的具体数值一一对应.如果收到的(f1,…,fn)落入不是一一对应的列，则译码失败.而非线性编码下的解码函数不具有一一映射性，如果落到一一映射的列，依然可以译码.所以，当信宿节点收到n个数据包时，如果数据包具有相关性，对应线性编码质.这就是“全有或全无”问题.当为线性函数时，总是解码失败，此时需要重传数据包.但是当为非线性编码时，还有一定的机会解码成功，此时不需要重传.这样，非线性网络编码节省了重传次数.

表2 线性函数编码时G不满秩时的解码函数Tab.2 The decoding function when G for linear function is not full rank

表3 非线性函数编码时不是一一映射时的解码函数Tab.3 The decoding function when non-linear function is not one-to-one mapping

2.2.2 非线性编码的纠错

线性编码的纠错方案一般通过加入一定的冗余来识别错误.线性纠错码里，为了增加检错或纠错能力，在信息里增加多余的码元，以扩大码字之间的差别，新增加的多余码元即为冗余.在此时需要传输的消息记为u=(u1,u2,…,uk)，通过一个(n,k)的最大距离可分码的生成矩阵对u=(u1,u2,…,uk)进行编码，编码后的消息向量为X=(X1,…,Xi,…，Xn).此时冗余的大小为n-k.此编码的最小距离为n-k+1.如果是点对点通信，只要错误个数t满足t≤(n-k)/2，则以可正确译码.但在线性网络编码中因为中间节点的混合操作使得t个错误发生扩散，扩散后的错误个数可能远远大于t，所以不能译码[10, 11].

如果是非线性网络编码，设计一个和线性编码的生成矩阵对应的编码函数矩阵.编码过程如下.

(7)

其中·为复合函数操作.只要函数β1,β2,…，βn之间的独立性达到最大，则其可以对抗尽可能多的错误.当β1,β2,…，βn为线性函数时，则此编码退化为线性编码时的生成矩阵.非线性的函数个数远远大于线性函数个数，β1,β2,…，βn之间的汉明距离更大，所以对抗的错误更多.这一性质可以局部改善线性网络编码对抗错误能力弱的问题.

3 仿真

对比纯路由传输，线性网络编码和非线性网络编码三种传输方案的正确译码率以及能量消耗.q大小设置为2，3，5，7，以2为主.q如设置太大，编码向量太长，将加重通信负担.

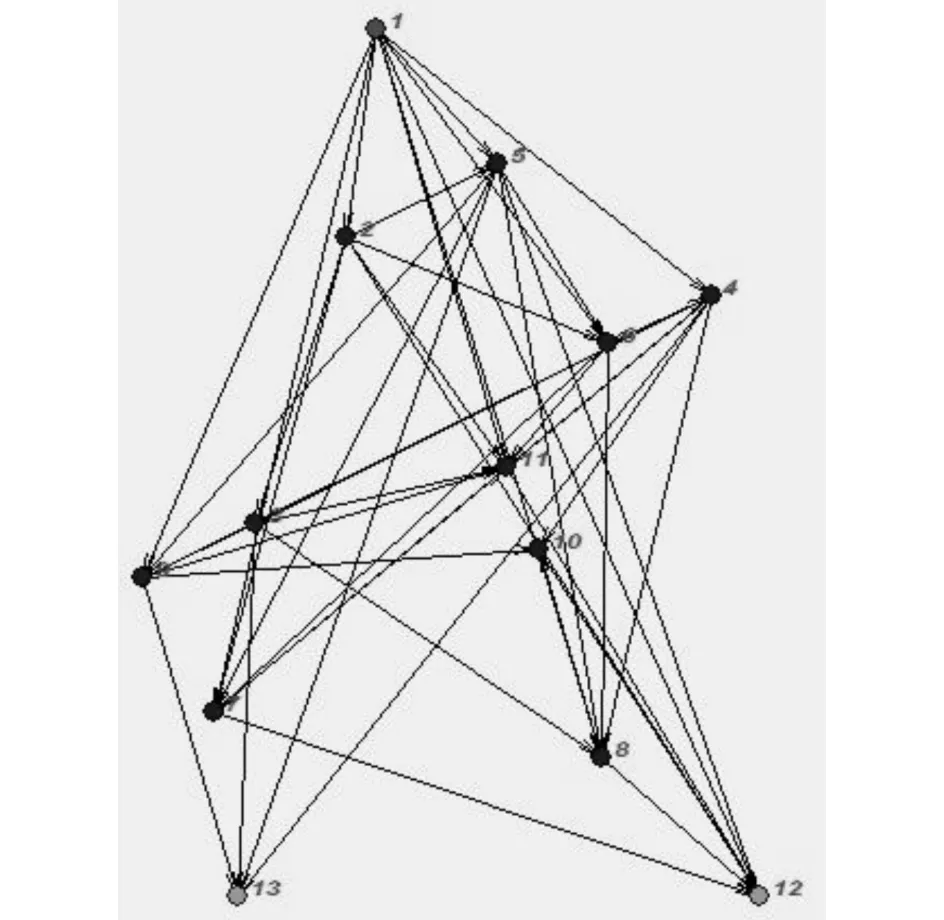
图3 多播网络的拓扑Fig.3 The topology of a multicast network

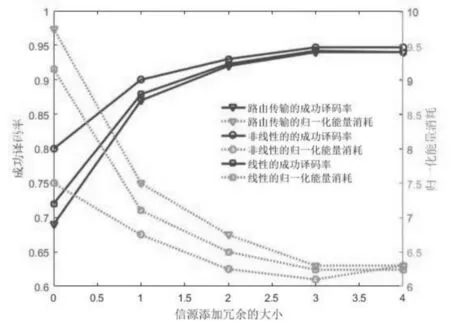
图4 三种传输方案对比Fig.4 The comparison among three transmission schemes

图3是实验采用的一个多播网络的拓扑.在图3里，深色的节点1表示信源节点，浅色的节点12,13表示两个信宿节点.其余的节点为中间节点，总的节点数13.拓扑由拓扑生成器随机生成的.拓扑生成器是Visual C++编写的一个拓扑生成软件.图 4表明，译码的成功率和能量消耗随着冗余的增加而变化的情况.其中能量评价函数采用文献[12]中的模型，其特点是用消耗的时间来表征消耗的能量.能量评价函数用公式

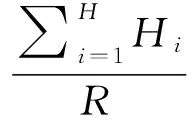
(8)

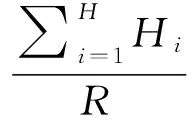
结果显示，随机非线性网络编码具有更高的成功译码率，更低的能量消耗.主要原因是即使受到消息之间相关性的影响，非线性网络编码仍有一定机会恢复原始消息.当有错误存在时，其能容纳更多的错误.以上两点减少了重传的机率，因而能量消耗也相应减少.

4 结语

相比线性网络编码，非线性网络编码较好地解决了“全有或全无”问题，也能纠正更多的错误.但其编码向量长，增加了一定的通信负载.解码算法基于查表法，效率有待提高.相比线性网络编码，非线性网络编码还有更多的潜力有待开发.

[1] Li S Y, Yeung R W, Cai N. Linear network coding [J]. IEEE Transactions on Information Theory, 2003, 49(2):371-381.

[2] 姚世雄，陈 晶，向 琨，等.网络编码理论及应用综述[J].中南民族大学学报(自然科学版)，2017，36(2)：115-128.

[3] Wang L, Yang Z, Xu L, et al. NCVCS: Network-coding-based video conference system for mobile devices in multicast networks [J]. Ad Hoc Networks, 2016, 45:13-21.

[4] Lehman A R, Lehman E. Complexity classification of network information flow problems [C]// ACM.15th Acm-Siam Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics. New Orleans:ACM,2004:142-150.

[5] Kwon M, Park H, Frossard P. Compressed network coding: Overcome all-or-nothing problem in finite fields [C]//IEEE. Wireless Communications and Networking Conference. Istanbul:IEEE, 2014:2851-2856.

[6] Yan Z, Xie H, Suter B W. Rank deficient decoding of linear network coding [C]// IEEE. International Conference on Acoustics, Speech and Signal Processing. Florence: IEEE, 2013:5080-5084.

[7] Sanna M, Izquierdo E. A survey of linear network coding and network error correction code constructions and algorithms [J]. International Journal of Digital Multimedia Broadcasting, 2011:1687-7578.

[8] Shang T, Zhang C, Li K, et al. Nonlinear quantum network coding with classical communication resource [C]// IEEE. GlobeCOM Workshops. San Diego: IEEE, 2015:1-6.

[9] Katti S, Rahul H, Hu W, et al. XORs in the Air: Practical wireless network coding [J]. IEEE/ACM Transactions on Networking, 2008, 16(3):497-510.

[10] Langberg M, Effros M. Network coding: Is zero error always possible? [C]//IEEE. Communication, Control and Computing. Monticello: IEEE, 2012:1478-1485.

[11] Gadouleau M, Yan Z. Packing and covering properties of subspace sodes for error control in random linear network coding [J]. IEEE Transactions on Information Theory, 2010, 56(5):2097-2108.

[12] Z. Guo, B. Wang, P. Xie, et al. Efficient error recovery with network coding in underwater sensor networks [J]. Ad Hoc Networks, 2009, 7: 791-802.

StudyonRandomNon-linearNetworkCoding

ZhangDongqiu

(School of Computer and Information Technique, Mudanjiang Normal University, Mudanjiang 157011,China)

The error-correcting capacity of the linear network coding is limited, and the concept of non-linear network coding is presented. A new concept of non-linearly independent is presented to replace the existing concept of linearly independent. When the

symbols are non-linearly dependent, there is a fair possibility to decode the original messages without receiving more symbols. This scheme is just to utilize the pre-existing dependent symbols reasonably to decode original messages, instead of re-transmitting new symbols. Moreover, network coding is performed over binary field to save computational overhead. The simulation results show that this scheme reduces much energy and has low time delay.

network coding; non-linear; error-correcting

2017-09-20

张东秋(1983-)，女，博士，研究方向：计算机教育技术和传感器网络，E-mail：307642064@qq.com

国家自然科学基金资助项目(61571150)

TP39

A

1672-4321(2017)04-0116-05