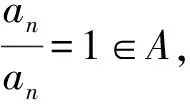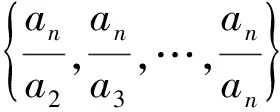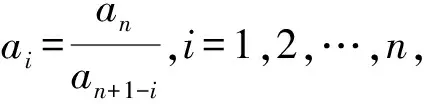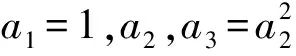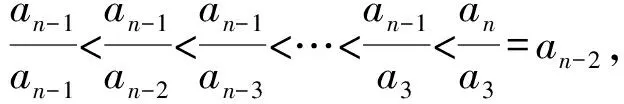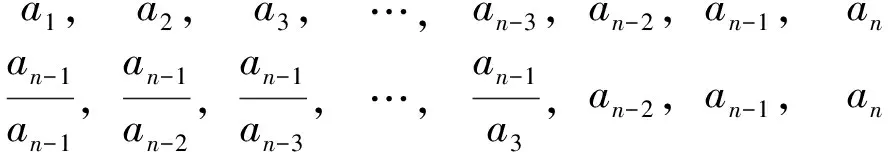等差数列和等比数列的另类刻画
2017-12-24李启超
李启超
(北京市十一学校数学教研组 100039)
1 试题的回顾与比较
2017年1月中旬举行的清华大学中学生标准学术能力测试数学部分(共40道不定向选择题)包含如下一道题目:
(2017年-清华能力测试-33题)已知a1,a2,…,an(n≥3)不是等差数列,且满足
①0≤a1 A.3 B. 4 C. 5 D. 6 事实上,本题有2009年高考理科北京卷压轴题和2014年北京市顺义区的一道高考模拟题的明显背景. (Ⅰ) 分别判断数集{1,3,4}与{1,2,3,6}是否具有性质P,并说明理由; (Ⅲ) 证明:当n=5时,a1,a2,a3,a4,a5成等比数列. (2014年-顺义二模-20题) 已知集合A={a1,a2,…,an}(1≤a1 (Ⅰ) 分别判断集合M={0,2,4}与N={1,2,3}是否具有性质Q; (Ⅲ)当n=3,4或5时集合A中的数列{an}是否一定成等差数列? 说明理由. 试题的赏析与探究2009年北京高考数学压轴题第(Ⅲ)问要求考生证明满足性质P的有限数列{a1,a2,a3,a4,a5}是等比数列,题干简洁,结论优雅,令人耳目一新. 作为这道题的变式题,2014年顺义区二模压轴题将等比数列的性质P巧妙地迁移到等差数列情形,结论也与等比数列情形类似.本文第二部分,我们将采用“有序化”和“一一对应”的策略,证明这两道题的推广形式,即:满足性质P的数列a1,a2,…,an(n≥3),在n≠4时一定是等比数列;满足性质Q的数列a1,a2,…,an(n≥3),在n≠4时一定是等差数列. 据此结论我们不难解答上面的三道试题. 本节我们证明上述问题的两个推广形式,相应的结论可以看作一类有限等差、等比数列的另类刻画. 命题1已知数集A={a1,a2,…,an} anan>anan-1>…>ana2>an, 可知B∩A=∅,根据性质P,有 我们得到集合A中元素的一个重排,如下方数表所示: a1,a2,a3,…,an-3,an-2,an-1,ananan,anan-1,anan-2,…,ana4,ana3,ana2,ana1, ai·aj+1=an, 1≤i≤j≤n-1,i+j=n, (1) 特殊地,a2·an-1=an,a3·an-2=an. 当n>4时,我们考虑集合C={an-1an-1,an-1an-2,…,an-1a3},这时集合C中有n-3个元素. 因为an-1an-1>an-1an-2>…>an-1a3>an-1a2=an,由性质P可知 ={a1,a2,a3,…,an-3}, 于是我们得到如下数表(这里要求n>4): a1,a2,a3,…,an-3,an-2,an-1,anan-1an-1,an-1an-2,an-1an-3,…,an-1a3,an-2,an-1,an ai·aj=an-1, 1≤i≤j≤n-1,i+j=n, (2) 比较(1)(2)两式,我们得到 于是,数列a1,a2,…,an(n≥5)是首项a1=1, 公比q=a2的等比数列; 当n=4时,任意集合{1,a1,a2,a1a2},a2>a1>1满足性质P,但不一定为等比数列. 证毕. 说明1文献[1]中通过分类讨论n的奇偶性证明了相同的结论. 命题2已知数集A={a1,a2,…,an}(0≤a1 证明本题证明与上一题类似. 我们取A中最大的数an,由an>0,an+an∉A,所以an-an=0∈A,于是A中最小数a1=0. 考虑集合 B={an+a2,an+a3,…,an+an}, 因为 an+an>an+an-1>…>an+a2>an, 可知B∩A=∅,根据性质Q,有 {an-a2,an-a3,an-a4,…,an-an}⊆A, 又因为an-a1∈A,且an-a1>an-a2>an-a3>…>an-an,我们得到集合A中元素的一个重排,如下方数表: a1,a2,a3,…,an-2,an-1,anan-an,an-an-1,an-an-2,…,an-a3,an-a2,an-a1 在这个2×n数表中,每一列的数两两相等,也就是ai=an-an+1-i,i=1,2,…,n,我们将它等价地表述为 ai+aj+1=an, 1≤i≤j≤n-1,i+j=n, (3) 特殊地,a2+an-1=an,a3+an-2=an. 容易知道,当n=3时,a1=0,a2,a3=2a2成等差数列; 当n>4时,我们考虑集合C={an-1+an-1,an-1+an-2,…,an-1+a3},这时集合C中有n-3个元素. 因为an-1+an-1>an-1+an-2>…>an-1+a3>an-1+a2=an, 由性质Q可知 {an-1-an-1,an-1-an-2,an-1-an-3,…,an-1-a3}⊆A,n≥5, 又因为an-1-an-1 {an-1-an-1,an-1-an-2,an-1-an-3,…,an-1-a3}={a1,a2,a3,…,an-3}, 于是我们得到如下数表(要求n>4): 在这个2×n数表中每一列的数都是相等的,从而ai=an-1-an-i,i=1,2,…,n-3,并且,a2=an-1-an-2⟺a2+an-2=an-1,a1+an-1=an-1. 我们将这几个式子等价地表述为: ai+aj=an-1, 1≤i≤j≤n-1,i+j=n, (4) 比较(3)(4)两式,我们得到aj+1-aj=an-an-1=a2,j=1,2,…,n-1. 于是数列a1,a2,…,an(n≥5)是首项a1=0, 公差d=a2的等差数列; 当n=4时,任意集合{0,a1,a2,a1+a2},a2>a1>0满足性质Q,但不一定为等差数列. 证毕. 说明2事实上,等差数列和正数等比数列相差一个对数变换,因而命题2和命题1在本质上是同构的.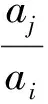

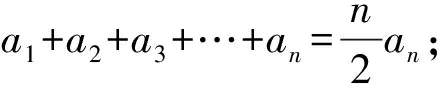
2 等差数列和等比数列的另类刻画