数学问题解答

(解答由问题提供人给出)

2371已知实数a,b,c都不等于1，且满足abc=1,求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

可以用做差证法，事实上

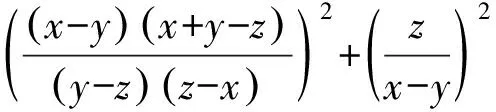
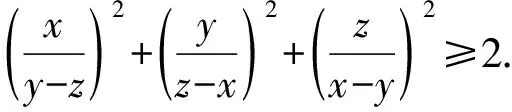
2372已知：如图，AB、AC1、AC2、AE为逆时针排列的四条弦，且AB为⊙O的直径，∠BAC1=∠EAC2.

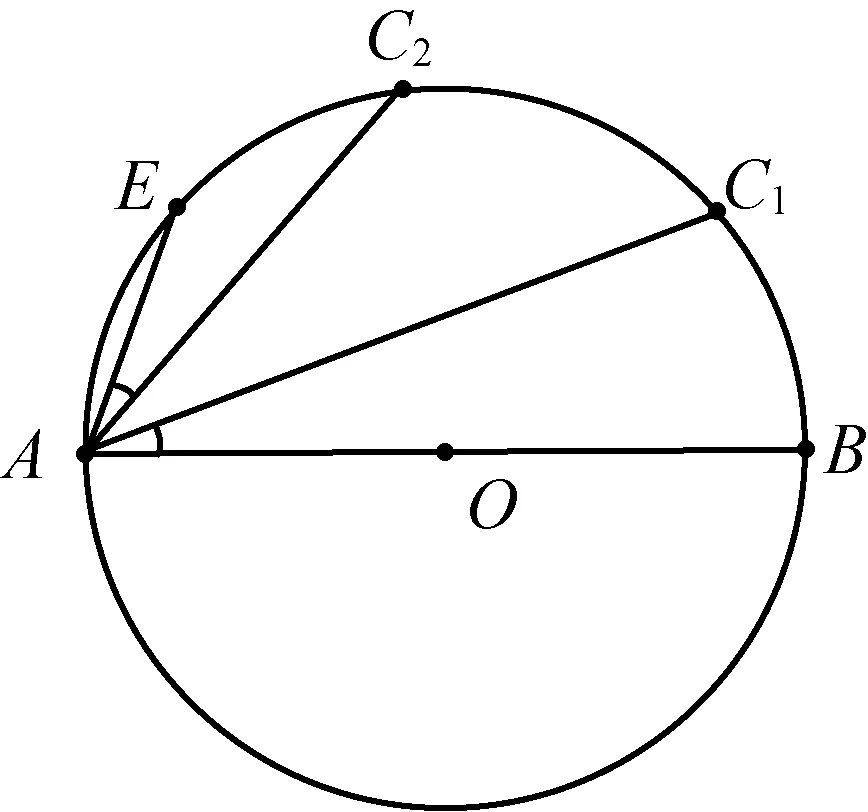
求证：2AC1·AC2≤AB2+AB·AE.

(北京市朝阳区芳草地国际学校富力分校 郭文征 郭璋 100121)

证明如图，连接C1C2并延长与AE的延长线交于点D.

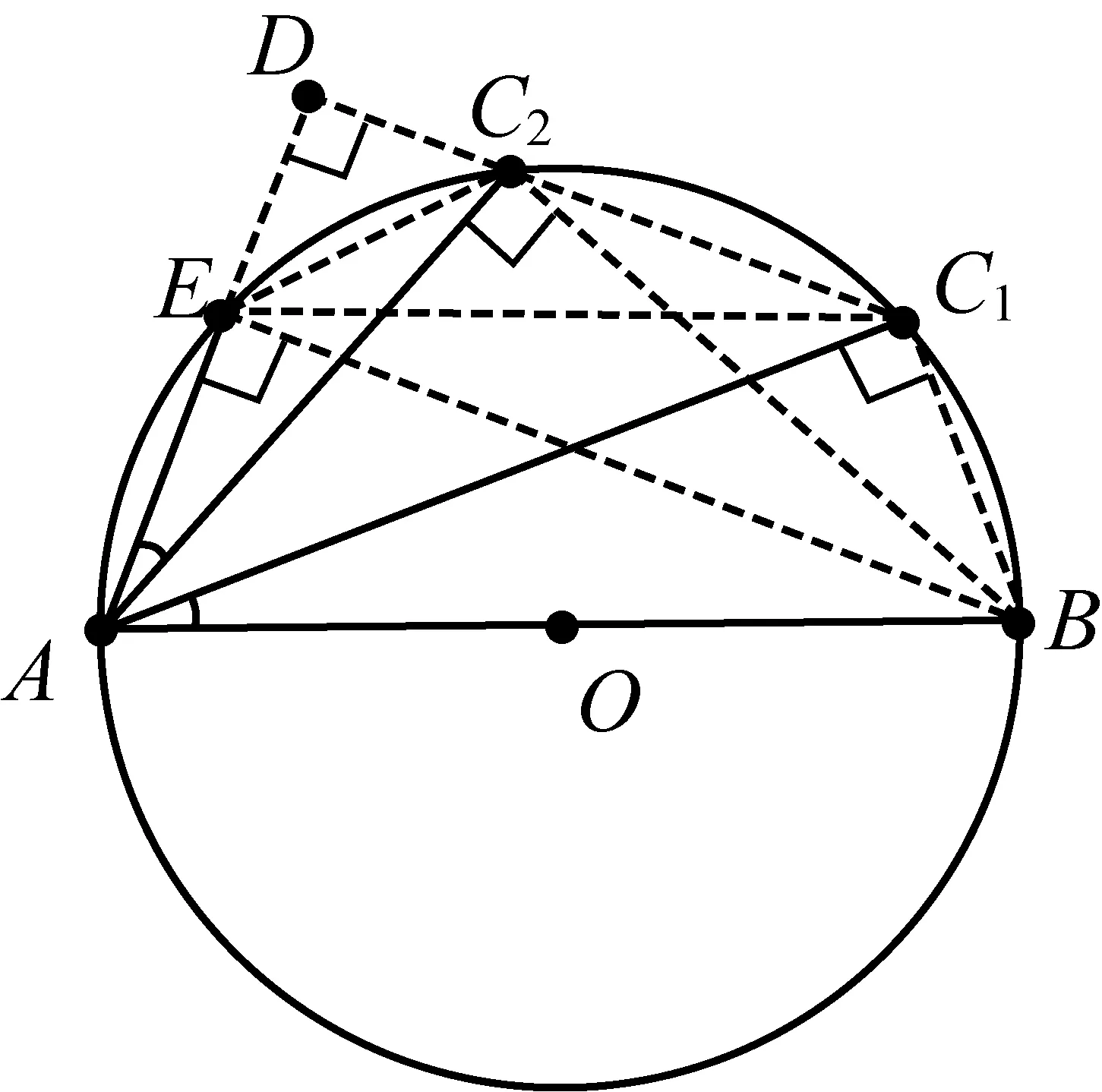
连接EC2、EC1、EB、BC1、BC2，

则∠AEB=∠AC2B=∠AC1B=900.

因为∠BAC1=∠EAC2，

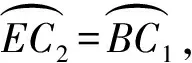
所以 ∠AEB=∠ADC2=900.

所以Rt△ADC2∽Rt△AC1B.

⟹AC1·AC2=AB·AD=AB·(AE+ED)

=AB·AE+AB·ED……①

因为点A、E、C2、B四点共圆，

所以∠DEC2=∠ABC2.

所以Rt△EDC2∽Rt△BC2A.

⟹AB·ED=BC2·EC2.

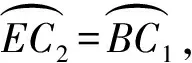
所以AB·ED=BC1·BC2.……②

由①与②得

AC1·AC2=AB·AE+BC1·BC2.

③

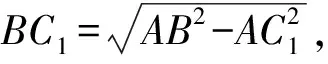
所以

⟹BC1·BC2

⟹BC1·BC2≤

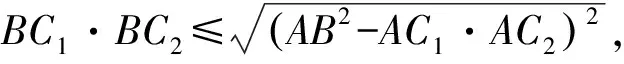
⟹BC1·BC2≤AB2-AC1·AC2.……④

由③与④得

AC1·AC2≤AB·AE+AB2-AC1·AC2,

所以 2AC1·AC2≤AB2+AB·AE.

当且仅当AC1、AC2重合为∠BAE的平分线时，不等式中的等号成立.

2373在△ABC中，三内角A、B、C所对的三边长分别为a、b、c，面积为Δ，求证：

(a+b-c)2+(b+c-a)2+(c+a-b)2

(浙江省开化县第二中学 曹嘉兴 324300)

证明设a+b-c=x,b+c-a=y,c+a-b=z,则

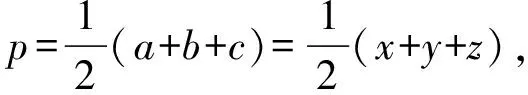
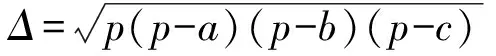
于是原不等式等价于

⟺2x2+2y2+2z2-(z-y)2

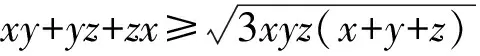
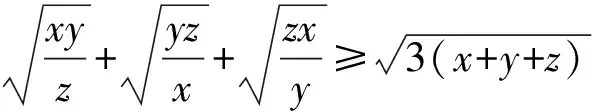
由二元均值不等式得

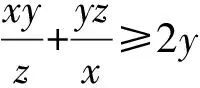
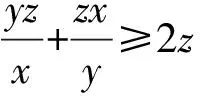
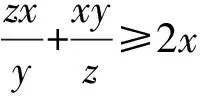
①+②+③得

故原不等式成立.

2374如图，△ABC的内切圆I分别切AB、AC、BC于点D、E、G,BC边上的高交DE于点H，若H为△ABC的垂心，求证：AH等于内切圆半径r.

(陕西省兴平市教研室 吕建恒 713100)

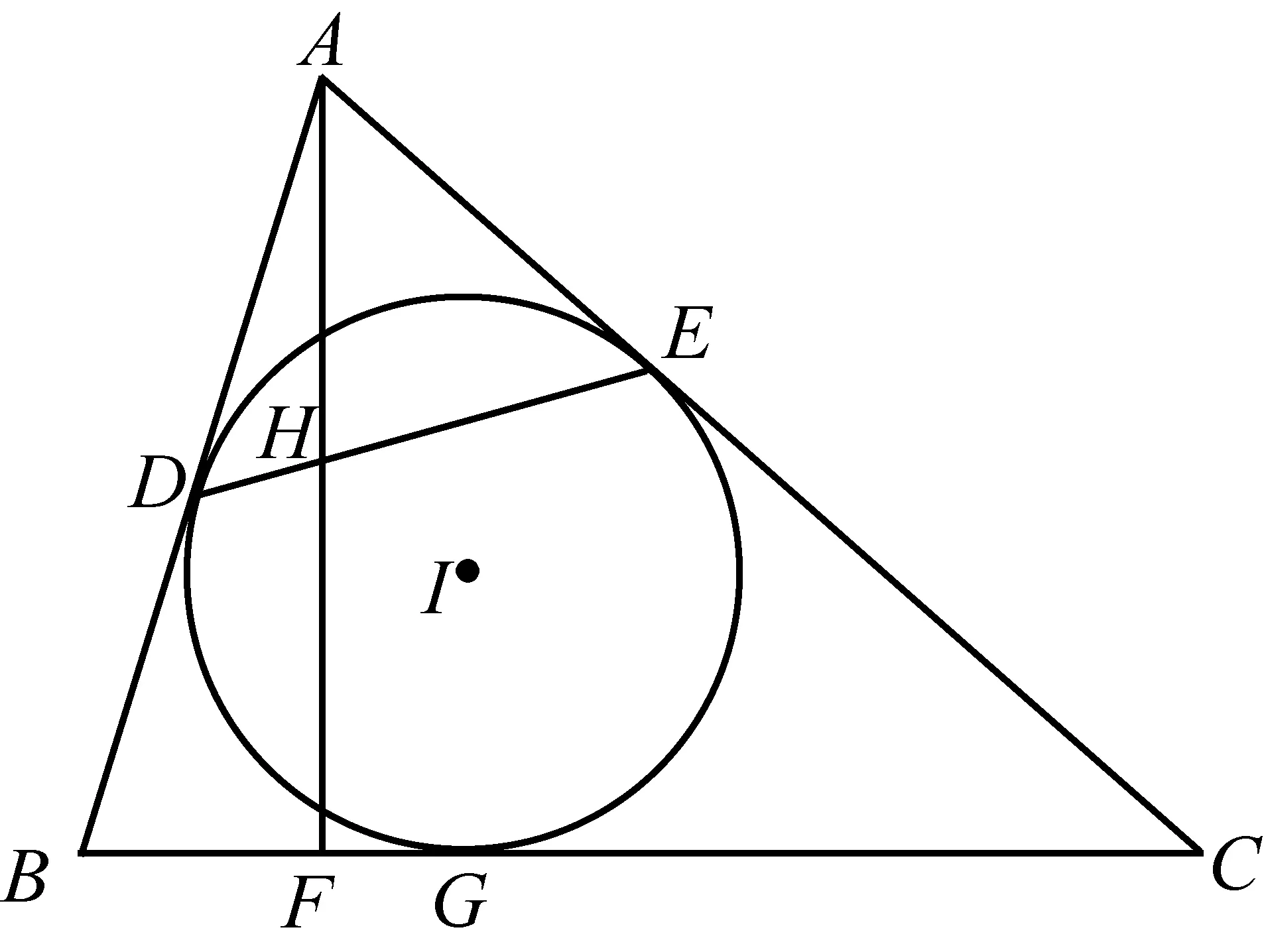
证明不妨设∠B≥∠C,连接BH、CH,

因为AD=AE，所以 ∠ADE=∠AED.

则 ∠BDE=∠CEH.

又因H为垂心，

所以 ∠DBH=∠ECH.

则 △BDH∽△CEH.

所以BH/CH=BD/CE.

所以BH/CH=BG/CG.

从而HG为∠BHC的角平分线，

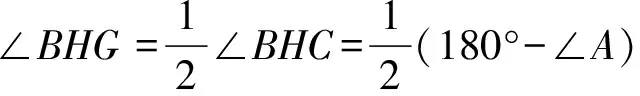
=90°-∠A/2=(∠B+∠C)/2.

注意 ∠FHG=∠BHG-∠BHF

=(∠B+∠C)/2-∠C=(∠B-∠C)/2,

又 ∠HAI=∠DAI-∠DAH=∠A/2-(90°-∠B)

=(∠B-∠C)/2,

所以∠HAI=∠FHG, 所以HG∥AI.

又因为AH∥IG,

所以四边形AHGI为平行四边形，

所以AH=IG=r.

2375在△ABC中，a,b,c；ta,tb,tc；分别表示三边长，内角平分线长，则有

(1)

(河南质量工程职业学院 李永利 467000)

证明设△ABC的半周长为p，面积为Δ，外接圆半径R，内切圆半径r，ha,hb,hc分别是三边a,b,c上的高．

先证左端的不等式

(2)

由ta≥ha,tb≥hb,tc≥hc

和三角形面积公式

及不等式

得

再由Δ=pr，abc=4Rrp，a+b+c=2p可得

即(2)式成立．

再证右端的不等式

(3)

由三角形内角平分线公式

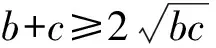
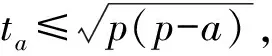
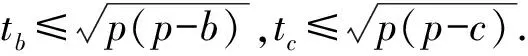
于是，由柯西不等式和恒等式abc=4Rrp，

a+b+c=2p,a2+b2+c2=2p2-8Rr-2r2，

及Euler不等式R≥2r可得

即(3)式成立．

由(2)，(3)两式可知不等式(1)成立．

2017年8月号问题

(来稿请注明出处——编者)

2376某委员会开了40次会议，每次有10人出席，而且委员会任两个成员都未在一起出席过一次以上的会议，证明：该委员会成员一定至少有82人.

(浙江省富阳市第二中学 许康华 311400；浙江省富阳市永兴中学 段春炳 311400)

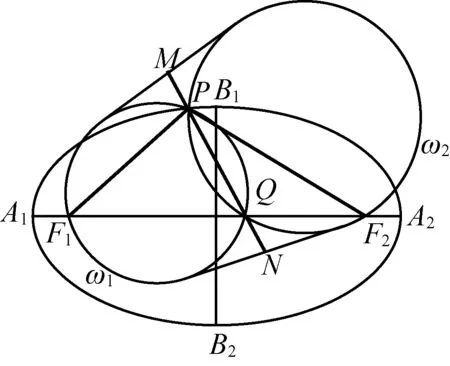
(河南省辉县市一中 贺基军 453600)

2378设正实数x1,x2,…,xn满足x1+x2+…+xn=s,且p≥1,求证:

(天津水运高级技工学校 黄兆麟 300456)

2379如图，在四边形ABCD中，DA、CB分别和圆O相切，切点A、B，AC交BD于H，F、E分别为DA、CB中点，当FE切圆O于G时,求证：

GH延长线平分AB．

(江西师范高等专科学校 王建荣 335000；温州私立第一实验学校 刘沙西 325000)