一个概率问题的解决及其启示

张红兵 龚卫东

(1.广州大学数学系 510006； 2.广东省深圳高级中学 518034)

有一道不起眼的概率题，由于一个不经意间的质疑，使它成为困扰学习者的难题.在尝试解决这个问题的过程中，我们找到了不同的解决方案，并深受启发，受益良多.

1 问题的提出

学习了古典概型后，一次测试中有这样一道习题：抛掷一枚硬币，若出现正面记1分，出现反面记2分.连续抛掷多次，恰好得3分的概率为多少？

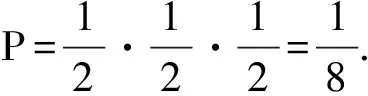
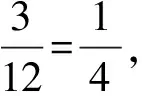
无奈之下，大家就采纳了教师A的意见,将问题限定在“连续抛掷3次”，但是要是不限定抛掷次数，无疑教师B的做法也是对的.这究竟是怎么回事呢？

2 问题的初步解决——由赛制得到的启发

要回答上面的问题，我们联想到了一个比赛问题：

势均力敌的甲、乙两人进行三局二胜制的比赛，求甲获胜的概率.

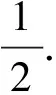
解法2甲获胜有两种情形：

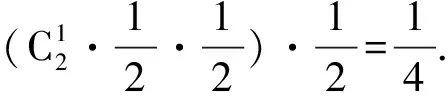
解法3考虑下表

三局比赛结果实际比分结果(胜,胜,胜)2:0(第3局没有实际发生)胜(胜,胜,负)2:0(第3局没有实际发生)胜(胜,负,胜)2:1胜(胜,负,负)1:2负(负,胜,胜)2:1胜(负,胜,负)1:2负(负,负,胜)0:2(第3局没有实际发生)负(负,负,负)0:2(第3局没有实际发生)负

我们发现解法2完全类似于教师B的解法，于是考虑把解法3运用于开头的问题，从而产生下面的虚拟解法(假设连续抛掷3次硬币)：

三次抛掷结果三次累计得分结果(正,正,正)1-2-33(正,正,反)1-2-44(正,反,正)1-3-4(第3次没有实际发生)3(正,反,反)1-3-5(第3次没有实际发生)3(反,正,正)2-3-4(第3次没有实际发生)3(反,正,反)2-3-5(第3次没有实际发生)3(反,反,正)2-4-55(反,反,反)2-4-66

这样，我们用虚拟解法解决了样本空间的数目问题，说明了原题目没有问题.但是，这个问题带给我们更多深刻的思考与启示.

3 几点思考

3.1 关于样本空间

根据古典概型的定义，构成样本空间的各个基本事件是等可能的，这是构成样本空间的基本事件的必要条件.在最开始我们所讨论的问题中，前4个事件(抛掷2次)跟后8个事件(抛掷3次)做的不是同一件事，不是等可能的，它们不能构成样本空间.

进一步地，同一个古典概型问题的样本空间可以是不同的，可以根据所考虑问题的不同视角而确定不同的样本空间.

例在分别写有2，3，4，5，7，8的六张卡片中任取2张，把卡片上的两个数字组成一个分数，求所得分数是既约分数的概率.

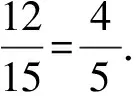
解法2两个数字构成的分数有30个：

3.2 数学语言的转化和翻译的解题功能

我们尝试将原问题的表述改为“抛掷一枚硬币，若出现正面记1分，出现反面记2分.连续抛掷多次，遇到得3分的概率为多少？”，把这个题目在实验班测试，而选取与这个班平行的另一个班级作为对照班同时进行测试，结果如下：

班别正确答题人数错误答题人数正答率实验班(更改后)33978.6%对照班(更改前)212051.2%

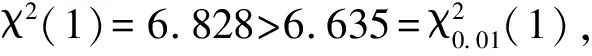
经过抽样座谈调查后发现，产生明显差异的原因在于，将“恰好得3分”改为“遇到得3分”后，就将学生的注意力由得分结果转移至实验过程，学生容易画出如下得分的树形图学生数学语言的理解与转化能力，目前尚未得到足够的重视.从这个案例可以发现，恰当地进行语言的翻译，有助于问题的解决. 数学语言是数学思维、数学理论的载体，将深奥的数学语言翻译成与自己的认知实际相符的数学语言，有助于数学解题能力的提高[1].中学数学中常见的还有诸如利用原命题与其逆否命题的等价性，将问题转化为与之等价的逆否命题进行解决，就涉及到语言的翻译问题.再比如数学问题中的集合语言、图形语言、文字语言的翻译，也有助于问题的解决.

习题本身的语言表述也很重要.一个好的表述应该是完整、严谨、规范的，做到明确而清晰、准确而不产生歧义，营造轻快、简洁的语言环境，让学生能专注于题目本身，尽情发挥平时所学.那些语言表达含混不清、甚至故设机关的习题，容易使学生产生歧义和误解，人为地造成学生理解上的困难，导致学生无所适从，会严重地削弱学生学习数学的兴趣，贻害无穷.

3.3 “回到定义”具有加深概念理解和解题功能，兼具研究价值

在本案例中，在解决有关“独立事件的概率”这一问题时，我们回到了最原始的概率的定义中去，运用了虚拟算法、列表法、树形图等数学方法和工具，还深化了对于古典概型以及样本空间概念的认识，足见“回到定义”的威力.

波利亚在其名著《怎样解题》中认为：回到定义上去是一项重要的思维活动[2].他认为“回到定义去”是为了掌握那些在专业术语后面数学对象间的实际关系,是变更问题的特殊手段之一.因此,我们解决有关问题时,不妨常常“回到定义去”.

“回到定义”还具有引导研究的作用.读书、做题是手段，研究学问是目的[3].中学数学教育中“研究性学习”、课题研究已深入人心、日益普及.但是如何研究、如何发现问题是研究得以真正展开的瓶颈和制约.中学生的所谓“研究”，要么是调查分析、一题多解、一题多变、解题反思，要么是盲目冒进，研究高等数学或者数学建模问题.这种“研究”，或流于肤浅，或因其难度之大而给学生留下“做研究太难”的印象，从而产生畏怯心理.如果我们能引导学生养成“回到定义”的习惯，让他们从定义出发研究诸知识或定义之间的关系与联系，有助于学生发现问题、解决问题，做力所能及的研究和“学问”.