直线方程、倾斜角与斜率的教学实践与反思
2017-12-24伍春兰
伍春兰
(北京教育学院数学系 100120)
2016年底,笔者以“直线方程、倾斜角与斜率”为题,在某地著名中学给高一学生上了一节课. 学生的数学学习基础良好,成绩优秀.
直线方程的概念本质上是刻画直线与方程的一一对应的关系,这是解析几何可以用方程(代数)研究直线(几何)的基础. 虽然直线方程的概念有些抽象,但思考问题的角度和方法都是数学味道的体现. 直线的倾斜角与斜率概念、公式,作为事实性知识不难理解,如果就事论事直接给出,省时省力,但学生错失了一次思维体操的机会. 把学生思维参与作为一个重要指标,并且从解析几何入门课的身份考量,笔者就直线方程的概念、倾斜角概念、斜率定义及斜率公式四大教学要点反思.
1 直线方程的概念的了解
直线方程的概念有正反两方面含义:方程的直线(直线上点的坐标都是这个方程的解)和直线的方程(方程的解为坐标的点都是直线上的点). 概念的表述从字面上看似绕口令,如果照本宣科只讲其表,学生易被绕进去不知所云. 在多次教师资格考试中,笔者发现直线方程的概念不少考生把自己都讲糊涂了. 为规避难点,有的教科书不提直线方程的概念,转而默认直线与方程的一一对应关系. 将直线与其方程视为一体不去深究的好处是,减轻了学生的认知负荷. 但笔者主张有必要让中等水平及以上的学生思考直线与其方程的关系,理由有二:
第一,解析几何研究直线,就是借助坐标把直线(几何)问题转化为方程(代数)问题,通过方程(代数)运算研究直线(几何)的性质. 问题是直线转化为方程是否“充分必要”,而“充分必要”是数学教学应该培养的基本思维习惯,特别是高中.
第二,直线是解析几何研究的最简单的曲线,也是第一个研究的曲线,直线和方程的形与数的关系学生是有基础的,因为他们在初中学过一次函数,并画过具体的一次函数图象. 基于学生已有的经验,是可以让他们接受的,人民教育出版社的普通高中课程标准实验B版教科书,就涉及了直线方程的概念[1].
1.1 直线方程的概念片段回放
先出示x-y-1=0,然后分步提问:(1)这个等式叫什么?(2)这个方程的解是什么?请举出两组解,并说明为什么是方程的解;(3)这两组解在几何上表示什么?(4)方程x-y-1=0所有的解在几何上表示什么(几何意义)?(5)反过来这条直线上任意一点满足方程x-y-1=0吗?
前4个问题,学生轻松破解. 问题(3)学生回答“点”时,笔者强调建立xOy直角坐标以后,有序数对(坐标)与平面上的“点”就建立了一一对应关系. 问题(4)学生回答“直线”时,追问“为什么”,学生能利用一次函数y=x-1说明. 问题(5)笔者借助GeoGebra平台,让学生观察直线上任意一点坐标,计算后发现满足方程x-y-1=0,由此指出(直线的)方程x-y-1=0与(方程x-y-1=0的)直线的一一对应关系.
接下来分别出示y-1=0、x-1=0,还是分步思考相应的问题(1)到问题(5). 在此基础上,归纳出直线方程的概念.
本环节最后,就解析几何创始人笛卡儿和费马,及解析几何基本研究方法做了简单介绍. 笛卡儿创建的坐标系是为了解决几何问题化归成方程问题的结晶,而问题的提出源自笛卡儿解决所有问题的一个理论假说:任何问题转化为数学问题,继而转化为代数问题,最终化归为方程的求解,这充分展现了“我思故我在”的笛卡儿兼具理性精神和创新品格.
1.2 直线方程的概念片段反思
本环节从一个具体的二元一次方程x-y-1=0出发,通过列举方程的解和平面上点的关系,继而将方程x-y-1=0变形为y=x-1,利用学生已有的一次函数y=x-1与直线的关系,得到方程x-y-1=0解的几何直观——直线. 然后利用信息技术,学生发现直线上的任意点的坐标也满足方程,完成方程x-y-1=0与直线一一对应的认识. 同时通过方程y-1=0、x-1=0,学生觉察到有些直线的代数表示未必能转化为一次函数(y=kx+b,k≠0),意识到直线方程概念的合理性. 至于直线方程(Ax+By+C=0,A、B不能同时为零)的抽象,留待学完“直线的方程”一节再让学生思考.
此设计特色有三. 第一,由学生熟悉的二元一次方程出发,从解的几何意义、与一次函数的关系等不同以往的思考角度,激发了学生的好奇心;第二,作为解析几何的首节课,舍得笔墨在直线方程的概念和数学史的相关内容上,将数学文化的理性和创新精神融入其中,并契合“了解”这一定位,为后面学习圆锥曲线方程的概念打下良好基础;第三,学生借助笛卡尔坐标这个桥梁,在初中学习的基础上,对“数”与“形”的联系有了进一步地认识.
2 直线的倾斜角的引入
角的定义有静态和动态两种,不同教材采用的倾斜角定义也有静态和动态之别,但笔者认为作为直线倾斜程度的刻画,简单合理为上,所以倾斜角使用静态定义更好.
2.1 直线的倾斜角片段回放
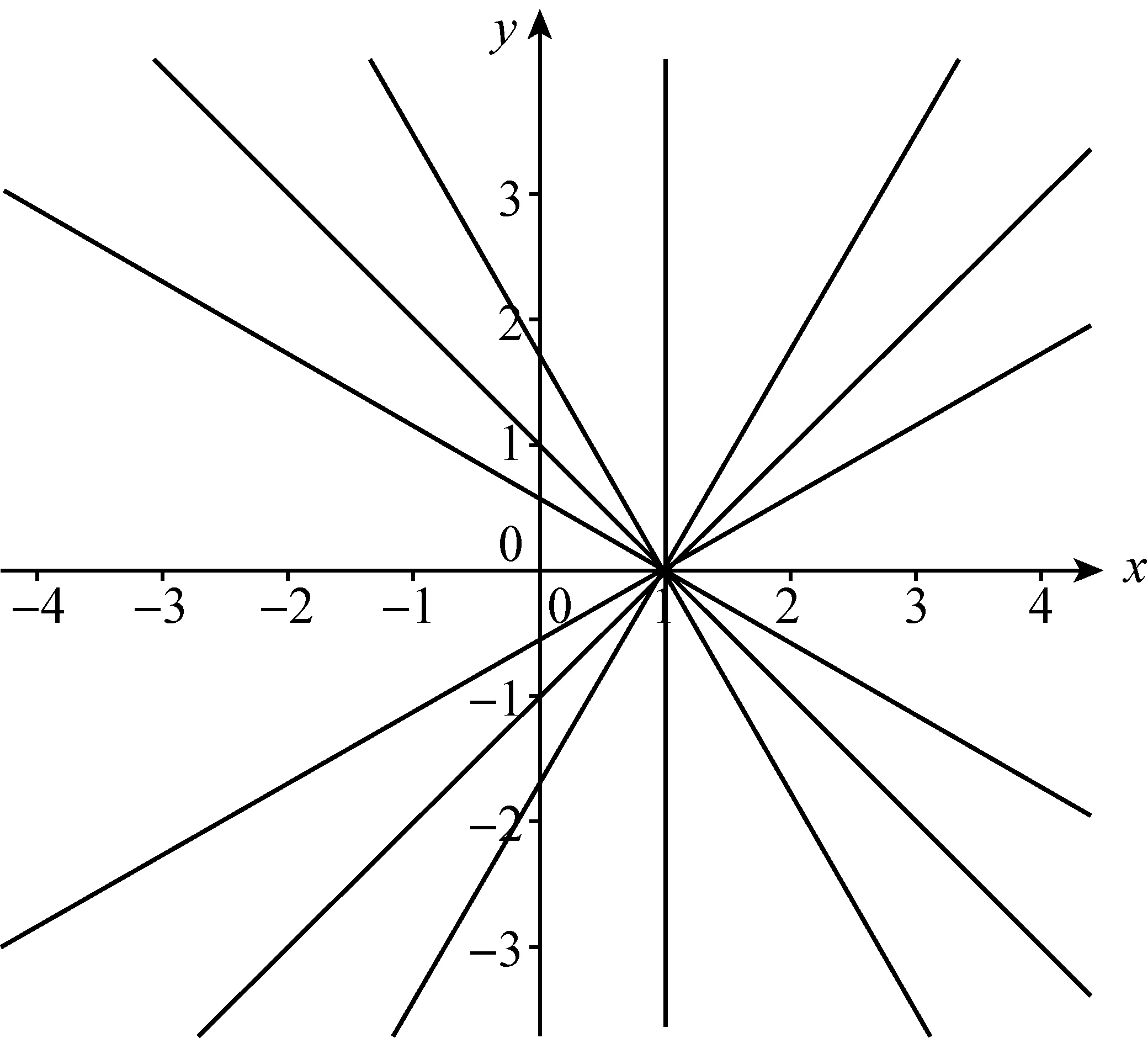
图1
出示图1提问:过(1,0)点的这些直线的差异是什么?学生回答:倾斜程度不同. 于是追问:倾斜程度相对谁?用什么量刻画倾斜程度?学生回答:x轴;角.
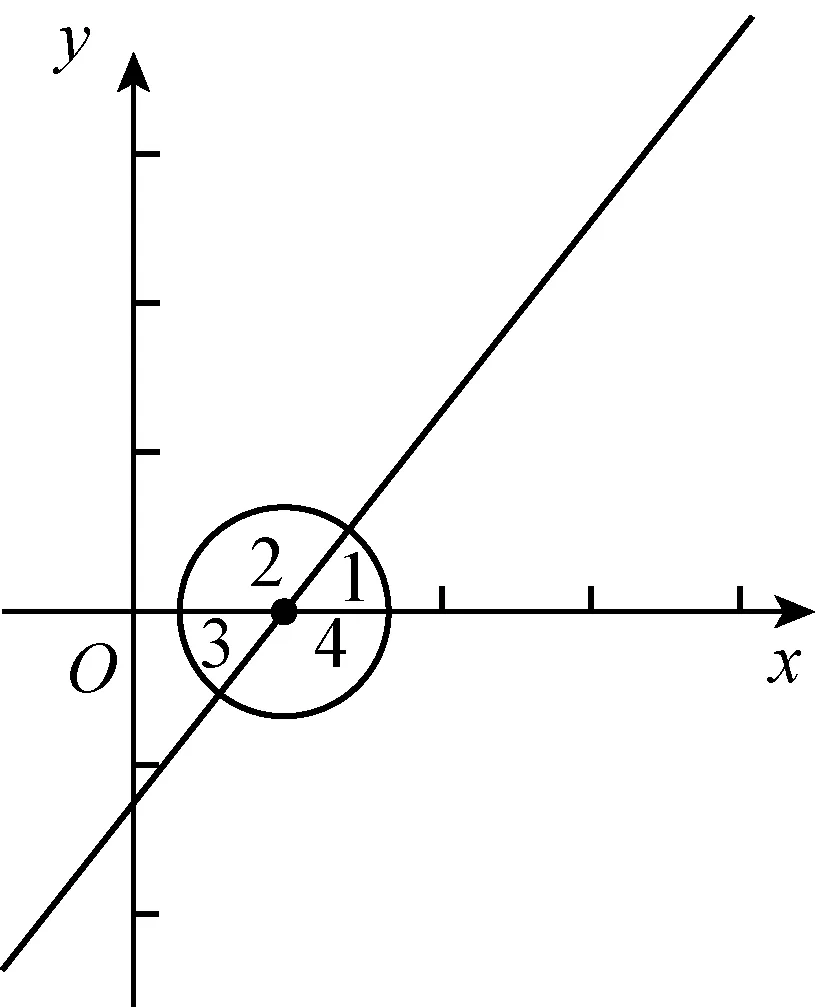
图2

图3

图4
接下来出示图2至图4,分步提出系列问题:选择图中∠1—∠4的哪个角刻画倾斜程度?如何给选定的角命名?如何用文字语言描述你所选定的角?特殊的直线(不与x轴相交)倾斜程度的角如何规定?刻画直线倾斜程度的角的范围如何规定?得出上述问题的答案你的理由是什么?
在学生独立思考基础上,小组交流,最后展示倾斜角的概念.
2.2 直线的倾斜角片段反思
出示图1用意有两点,一是发现过一点不能确定一条直线,二是相对某轴(线)的倾斜程度不同(习惯以x轴为基准).描述倾斜程度,除了“角”,还有“斜率”,学生不预习是不知道“斜率”的,也很难想到用比值表示. 可能会想到k(y=kx+b),因为学生在初中学习了一次函数,前面环节又借用了一次函数y=x-1与直线的关系. 但现场学生没有提出k,只指出了“角”,这样给“角”下定义的必要性就显现了:刻画直线的倾斜程度. 需要指出的是有的教材将直线斜率的概念先于直线的倾斜角,笔者不赞成这样的安排. 因为表示倾斜程度,对学生而言“角”比“斜率”更自然更直观,学生在课堂面对问题“用什么量刻画倾斜程度”,只有“角”的答案可以支持笔者的观点.
上述设计的系列问题,来源于倾斜角定义中所有规定的内容,需要学生决策(选择),具有一定的挑战性,又在其能力范围内,使他们积极投入到学习中,不仅经历了倾斜角“诞生”的全过程,也对定义的合理性有了较深认识,思维得到相应锻炼. 其中“用文字语言描述你所选定的角”,课堂上学生表达得不顺畅,因为用精准的文字语言描述概念对学生而言是难点.但这种磕磕绊绊的经历,才能使学生真正体会教科书上的定义之妙,让学生重视并较深入地理解概念,发现自己的不足(特别是学优生)促其成长.
其实还可以更开放,比如不出示图2至图4,先让学生思考直线与x轴的位置关系,自己画图再分别琢磨上述问题. 笔者考虑到与学生初次见面,还有很多同仁听课,以及时间紧等原因,所以没有采用后者的设计.
3 直线的斜率定义的构建
有的教材不用倾斜角的正切值界定斜率,益处是可以规避没有学习三角函数的尴尬. 但笔者主张还是用“直线的倾斜角α的正切值”定义直线的斜率k为好,理由是k=tanα(α≠90°)搭建了刻画直线倾斜程度的形(倾斜角)和数(斜率)之间的关系,使斜率有了几何直观. 由于倾斜角的范围:0°≤α<180°,而学生在初中学习过锐角三角函数,所以如果学生没有学习三角函数(必修4的内容),在需要时给出倾斜角为钝角时相应正切的公式即可.
不少教师仿某教材,类比“坡度”引出“斜率”概念,笔者认为值得商榷. “坡度”是学生学习“解直角三角形”(9年级下册)一章时,解决相关实际背景的习题时涉及的一个概念,教材直接给出. 笔者曾就“坡度”问题,随机寻问几位初中数学教师,他们都表示只是简单介绍一下概念,不会让学生做更多地思考. 例如,为什么斜面的“坡度”用坡面的“铅直高度”与“水平宽度”的比[2]-[3],而不用“铅直高度”与“斜面长度”的比表示(见图5),这样的问题教师不会有时间(面临中考)让学生探究的. “坡度”概念学生充其量只知其“表”不知其“本”,因此将“坡度”迁移到新概念(“斜率”),无助“斜率”的理解. 另外,“坡度”解释“斜率”定义的合理性也只局限在倾斜角为锐角的情形. 建议引入“斜率”概念后,再回顾“坡度”,说明“坡度”定义的合理性.
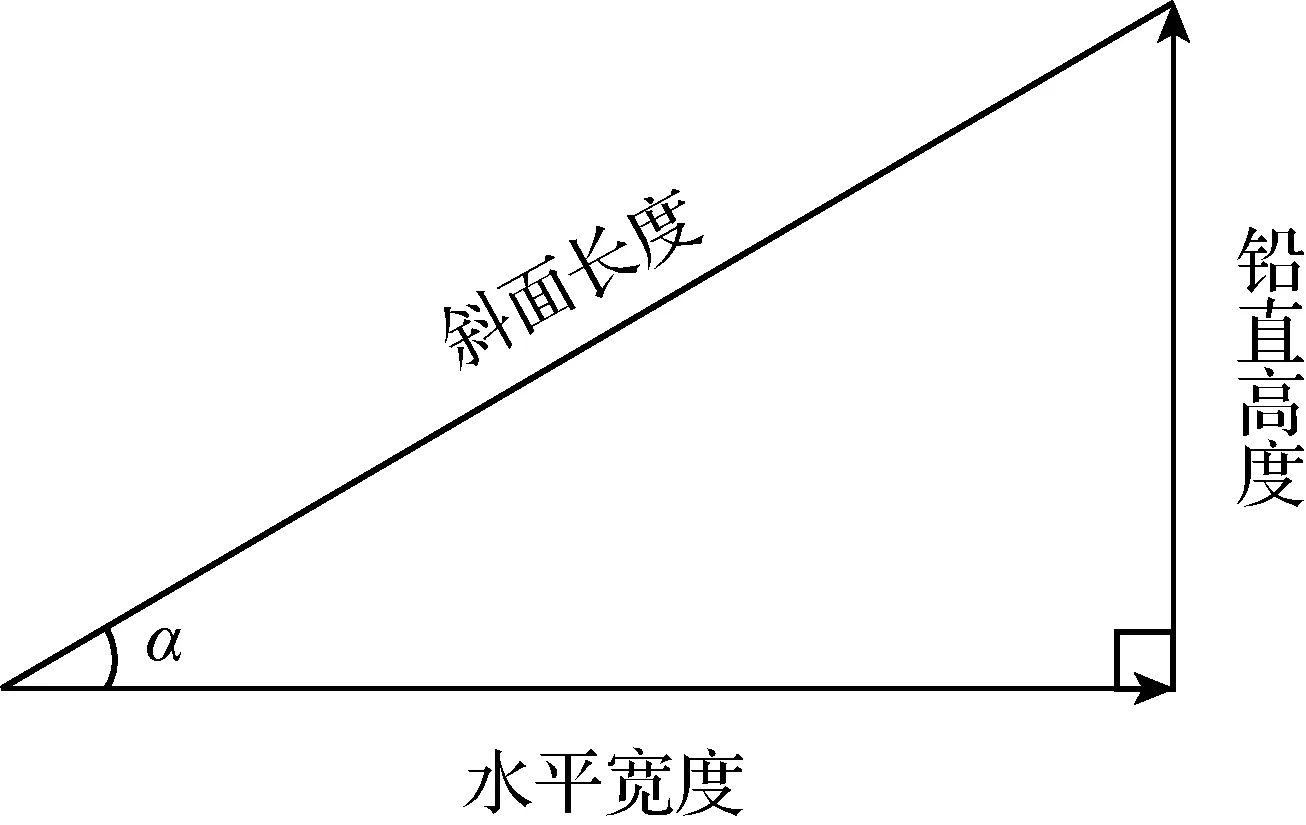
图5
3.1 直线的斜率定义片段回放
(1)请画过(1,0)、(2,1)两点的直线,并求其方程及倾斜角.
(2)请画过点(2,1)、倾斜角α为60°的直线,并求其方程. 思考:60°倾斜角在求直线方程过程和结果中是如何体现的?结合题(1),你有什么猜想?
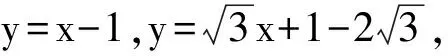
(3) 分别求直线方程y=kx+b的k:过A(2,1),倾斜角为α(0°<α<90°、90°<α<180°).
(4)当直线倾斜角α=0°、90°,(3)的结论是否成立?
学生得到k=tanα(α≠90°)并命名,然后教师解读斜率的含义并出示斜率定义.
3.2 直线的斜率定义片段反思
因为学生还没有学习怎样求直线的方程,此时他们只能借用初中的一次函数y=kx+b,通过待定系数求解.
题(1)不仅让学生体验了两点确定一直线外,还复习了待定系数求直线方程的方法,同时倾斜角的求解为后面的猜想做了铺垫. 题(2)需要将问题化归为题(1),即将倾斜角α为60°的条件,借助直角三角形通过正切找到另一个点. 观察题(1)、(2)求得的方程,学生易猜想k=tanα. 这一发现,让学生有些兴奋,一次函数解析式y=kx+b中k竟然与倾斜角α有瓜葛,点燃了学生进一步探究真伪的欲望. 题(3)将倾斜角α一般化,分类求k,其解决问题的方法与题(2)相同. 题(4)考虑特殊的倾斜角α=0°、90°的情形.
通过题(2)、(3)的求解,学生体会到一点、一倾斜角α能确定一直线,但是还要将倾斜角α转换成其正切值,而由题(3)、(4),表明k=tanα(α≠90°),此时为tanα下定义的必要性和合理性呼之欲出.
题(3)当倾斜角为90°<α<180°时,由于学生没有学习三角函数,所以给出诱导公式:tan(180°-α)=-tanα. 另外,题(3)、(4)倾斜角α的分类,完全可以交给学生思考. 与上一环节的顾虑一样,笔者没有采用后者的设计.
本设计的特点是“做中思”,且题目之间环环相扣一举数得,特别是为引出斜率公式(两点式) 找到生长点.
4 直线的斜率公式的设计
(1)提问1:倾斜角和斜率都是描述直线倾斜程度,它们的差异和联系是什么?
预设:差异是倾斜角是“形”,斜率是“数”;联系是k=tanα(α≠90°).
意图:明确倾斜角和斜率的差异和联系.
(2)提问2:不借助倾斜角,已知什么条件可以求斜率?理由是什么?
预设:已知两点;理由是:3.1环节题(1)的启示;两点定直线.
意图:让学生参与到问题的提出过程.
(3)提问3:已知两点求斜率如何用符号语言表述问题?
指导(有需要时):在直角坐标下,已知两点就是知道两点坐标.
预设:已知两点P1(x1,y1),P2(x2,y2),求直线P1P2的斜率.
意图:让学生经历将问题转化为数学问题的过程.
(4)提问4:上述问题先不考虑特殊情况(x1=x2或y1=y2),如何画出图形?需要分类吗?
指导:画图不必考虑点所在坐标的位置,只需考虑两点的相对位置及倾斜角的大小(分类).
预设:根据两点P1(x1,y1)、P2(x2,y2)的相对位置及倾斜角的大小(锐角、钝角),分为4类,见图6-图9.
意图:让学生经历将较复杂数学问题,通过分类,数形结合地解决问题的过程.

图6

图7

图8

图9
(5)提问5:请分别计算图6-图9中P1P2的斜率.
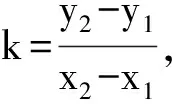
意图:学生能得到两点斜率公式,发现公式与两点坐标的顺序无关.
(6)提问6:请考虑特殊情况(x1=x2或y1=y2),斜率两点公式是否存在,并总结倾斜角、斜率、直线的关系.
预设:见表1
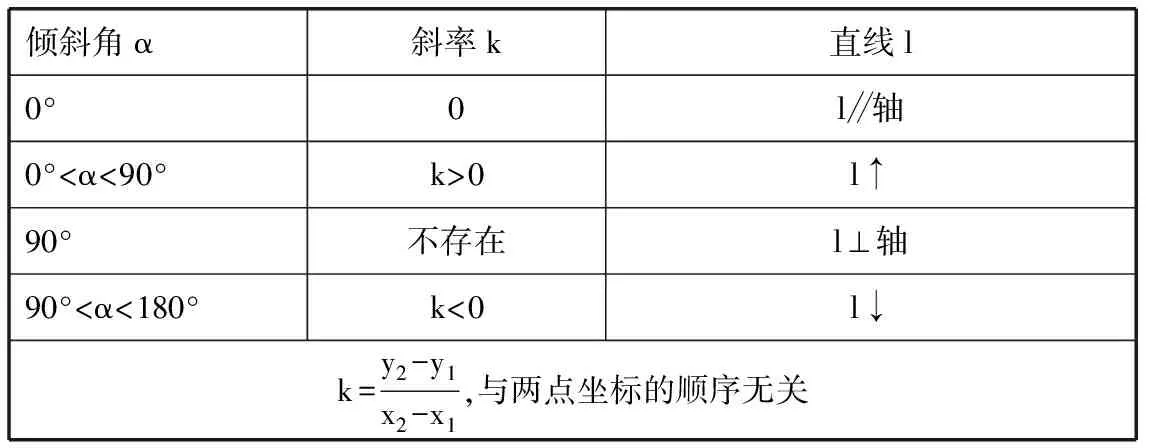
表1
意图:在教师指导下,学生梳理倾斜角、斜率与直线的关系.
遗憾的是一节课(40分钟)时间马上到了,此环节设计的活动匆匆掠过,学生没能充分参与.
5 结论
“直线方程、倾斜角与斜率”上述设计由两部分组成. 第一部分有一个概念(直线方程)、一段历史简介;第二部分有两个概念(倾斜角α;斜率k)、一个公式(斜率公式).
第一部分中的直线方程概念的教学意义,除了放心地将直线与其方程混为一谈,重要性在于让学生明白数学讲“理”,重视严谨,数学推演过程既要考虑充分条件,也要思量必要条件.
第二部分是教学重点,概念引入的必要性、界定的合理性;两个概念的共性、差异、联系、拓展(和导数的关系);公式的引入、推导等等都是具有数学味道的思考.
基于此,建议一气呵成连排两节课,多些学生的思维参与,少些教师的牵引替代.
