基于转矩分配的开关磁阻电机转矩脉动抑制的研究

杨 光， 杨明发， 石 凯

(福州大学电气工程与自动化学院， 福建 福州 350116)

基于转矩分配的开关磁阻电机转矩脉动抑制的研究

杨 光， 杨明发， 石 凯

(福州大学电气工程与自动化学院， 福建 福州 350116)

转矩脉动是开关磁阻电机亟待解决的问题和研究难点之一，其限制了速度控制性能和位置测量精度的进一步提升。基于转矩分配的开关磁阻电机转矩脉动抑制的理论研究已取得较大进步，但由于电机磁路的非线性，使得在实际应用中转矩很难准确反馈。本文根据电机的实际规格和尺寸，采用Maxwell3D计算出在不同转子位置和相电流下的转矩，建立了转矩-电流逆模型；通过合理地设置开通角、换相重叠角和关断角，简化了程序设计，抑制了反向制动转矩；进而根据转矩分配函数，采用电流闭环对转矩进行间接控制。仿真和实验结果证明了该方法可以有效地减小转矩脉动。

开关磁阻电机； 转矩脉动抑制； 转矩模型； 转矩分配函数

1 引言

开关磁阻电机(SRM)具有结构简单、成本低、效率高和调速性能好等一系列交流、直流调速系统的优点，已广泛地应用于纺织、电动汽车、家电、航空航天、矿山机械等领域。但是SRM的双凸级结构使得转矩和磁链是定子相电流和转子位置的非线性函数，无固定公式可循[1]，非线性磁路下脉冲工作方式的相电流导致SRM存在比较严重的瞬时转矩脉动，转矩脉动又会引起转速波动、降低位置控制精度，尤其在换相过程中更为明显。因此，加强瞬时转矩脉动抑制的研究是SRM发展的主要方向。

传统的电流斩波控制(CCC)、电压脉宽调制(PWM)和角度位置控制(APC)方式已取得较大进步，虽然这些控制方式适用转速范围宽、容易实现，但其均未考虑换相过程中合成转矩的平滑过渡，因此不能有效抑制换相转矩脉动[2]。基于转矩分配函数(TSF)的SRM转矩脉动抑制的理论研究已取得较大进步，但其在换相过程中，只有开通相的转矩可以通过控制电流实时控制，关断相的转矩只能随着电流的下降和转角的增加而无序变化，导致换相过程中合成瞬时转矩不能跟随目标转矩。文献[3]针对换相过程中关断相电流不可控而引起的转矩脉动增大的问题，提出减小或增大相电流进行转矩补偿的控制策略，实验结果表明该方法可有效抑制整距绕组分块转子SRM的转矩脉动。文献[4]提出了一种基于径向基函数(RBF)神经网络的SRM瞬时转矩控制方法，利用RBF神经网络运算速度快、泛化能力强的优点，从控制瞬时转矩出发对电流进行瞬时跟踪控制。文献[5]研究了开通角和关断角的合理控制可以有效抑制转矩脉动，其采用余弦型转矩分配函数，通过模糊优化开通角，在电流、转速双闭环的控制方式下对转矩脉动进行抑制，得到了比较好的仿真控制效果。文献[6]提出以各相电流为优化变量、以转矩误差最小为跟踪目标的一种新型转矩分配策略，但其算法复杂，实验未能实现。文献[7]设计了一种新型转矩分配函数， 通过改变分配函数中的波形系数来控制每相绕组的分配转矩，从而使实际转矩跟踪给定转矩，抑制电机运行时的转矩脉动。

综上所述，现有基于TSF的转矩脉动抑制的研究只侧重于控制方法的优良，忽略了最根本的转矩数据的准确性，而转矩模型的准确性直接影响系统的稳定性和控制效果的好坏。本文根据电机的实际规格和尺寸，采用Maxwell3D计算出不同转子位置和相电流下的转矩，通过和实测静态转矩相比较，验证了模型的准确性；然后利用插值法建立了转矩逆模型(i(Te,θ))，并根据转矩分配函数，采用电流闭环对转矩进行间接控制，有效地抑制了转矩脉动。

2 转矩模型

虽然SRM的结构简单，但其电磁关系却很复杂，磁路饱和、磁滞效应和涡流损耗等产生的非线性因素造成了SRM的数学模型难以建立。现有的SRM的线性模型和准线性模型突出了其基本物理特性，且具有便于定性分析、建模简单等优点，但是SRM实际工作在非线性状态。因此，为了提高转矩定量分析的精度，必须建立其非线性模型。

Ansys/Maxwell有限元计算软件目前已广泛应用于各种电机的磁场计算，其中SRM的二维有限元数值计算技术已经比较成熟，但其忽略了电机端部磁场效应，导致在齿对槽位置附近时，磁链和转矩的误差会达到30%以上，所以必须采用三维有限元分析。本文采用四相(8/6级)370W开关磁阻电动机，其主要结构参数如表1所示。

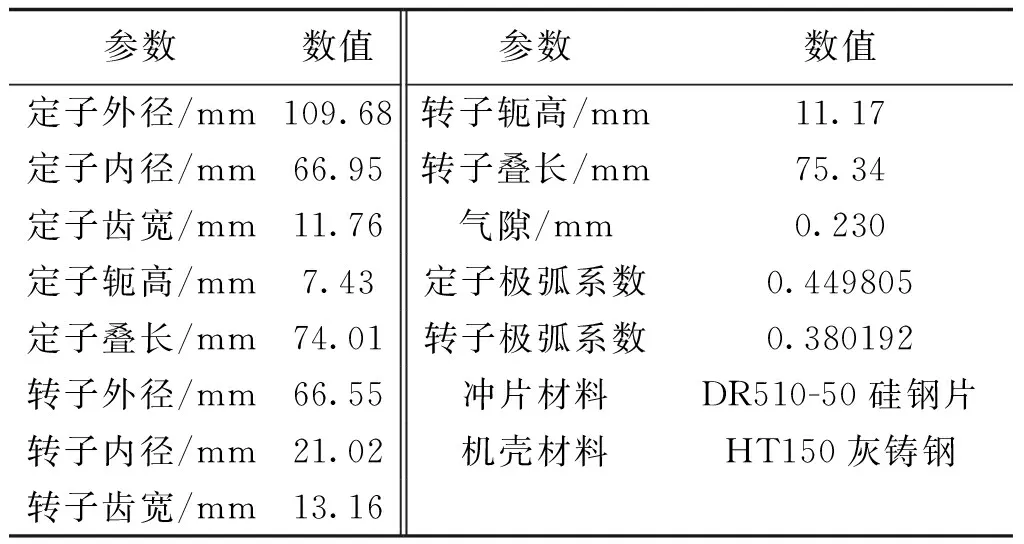
表1 电机结构参数

根据电机的实际规格和尺寸建立其三维仿真模型，如图1所示。在该模型下计算电机转矩和磁链时会充分考虑机壳和端部磁场效应产生的影响。

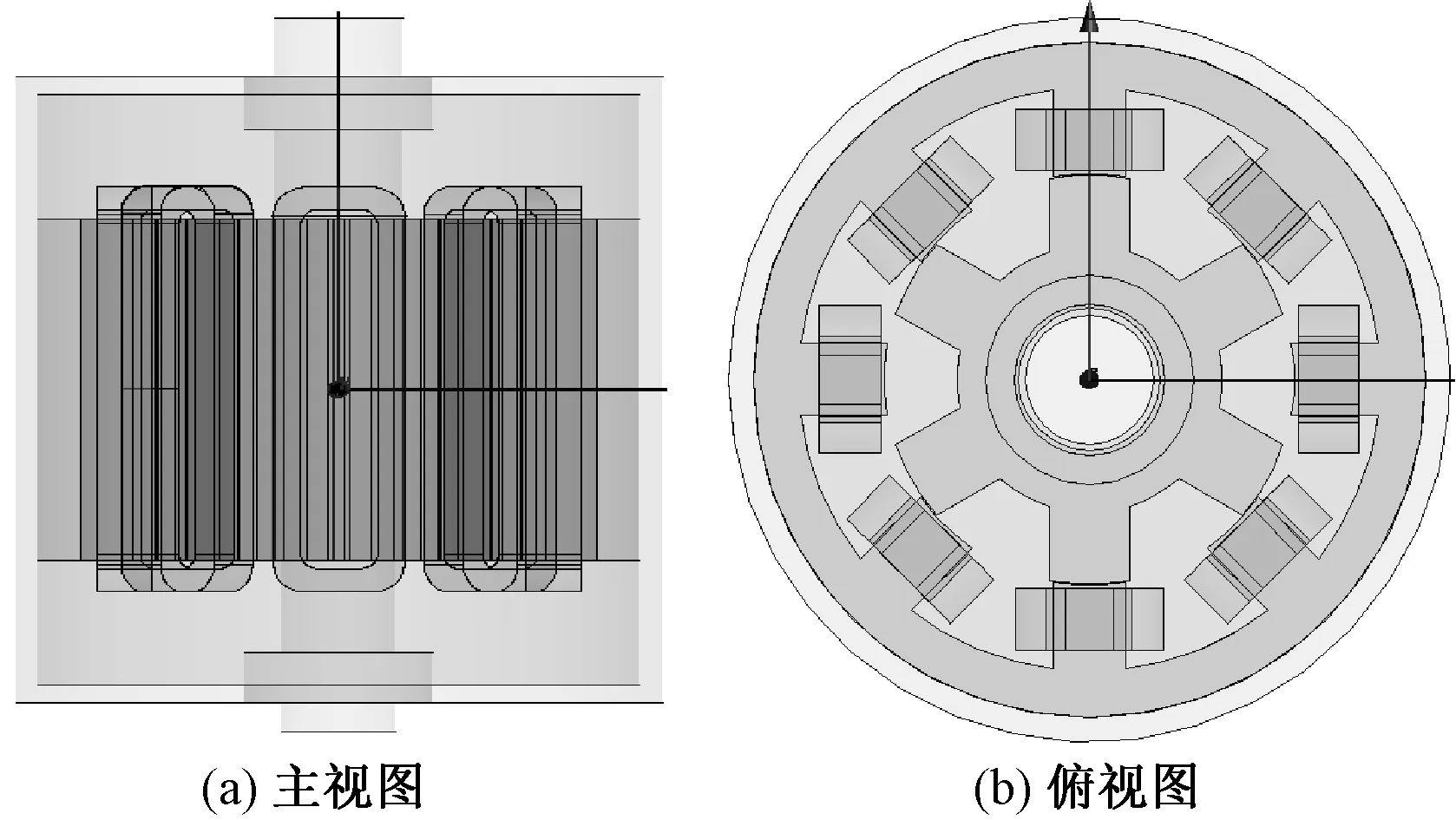
图1 实验电机模型Fig.1 Experimental motor model

基于TSF控制方法的通电方式是单相、双相交替导通，因此两种通电方式下的转矩波形都要考虑，但是两相通电产生的互感磁场对转矩的影响很小，可以忽略不计，因此，仿真和实验中总的转矩可以用四相转矩之和代替。

以A相绕组为例，为得到在不同相电流和转角位置下的转矩，分别给A相绕组通入步长0.2A、范围0～4A的电流，仿真计算出在固定相电流下转子位置0～60°的转矩值，进而可以绘制出转矩曲面，如图2所示。B相、C相和D相转矩依次相差15°机械角，将其相加即为四相合成瞬时转矩。

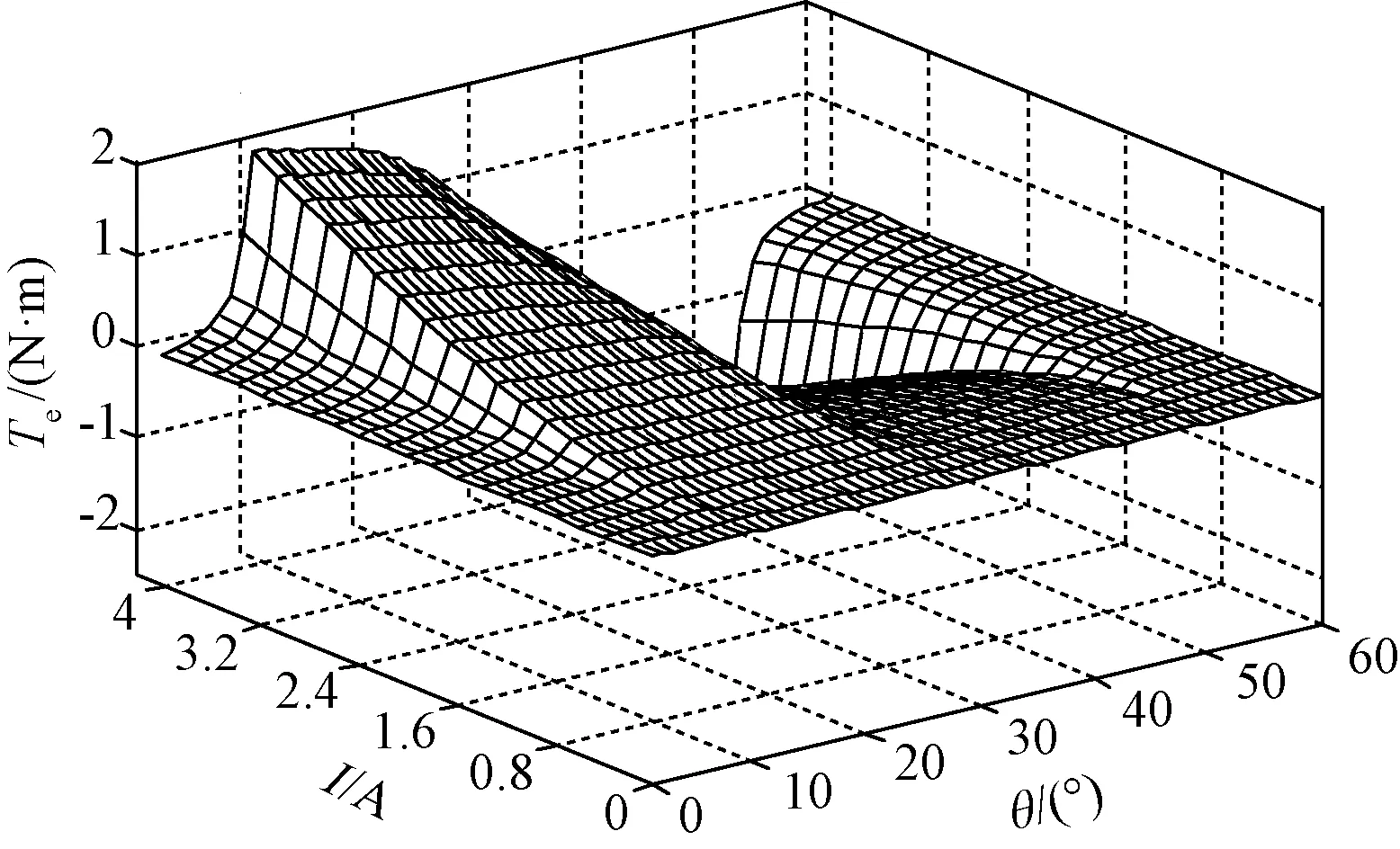
图2 根据仿真结果绘制的转矩曲面模型Fig.2 Curved surface model of torque based on simulation results

为了验证仿真计算出的转矩是否准确，需要测量实际情况下的静态转矩。使用分度盘固定实验电机的转轴在0°机械角位置(相对于A轴)，分别给A相通入步长0.2A、范围0～4A的电流，使用静态扭矩测量仪记录电机在0°转子角位置、不同相电流下的静态扭矩。按照上述方法，旋转转子角度，每隔2°测量一次在不同相电流大小下的静态转矩，可以得到如图3所示的转矩曲面模型。

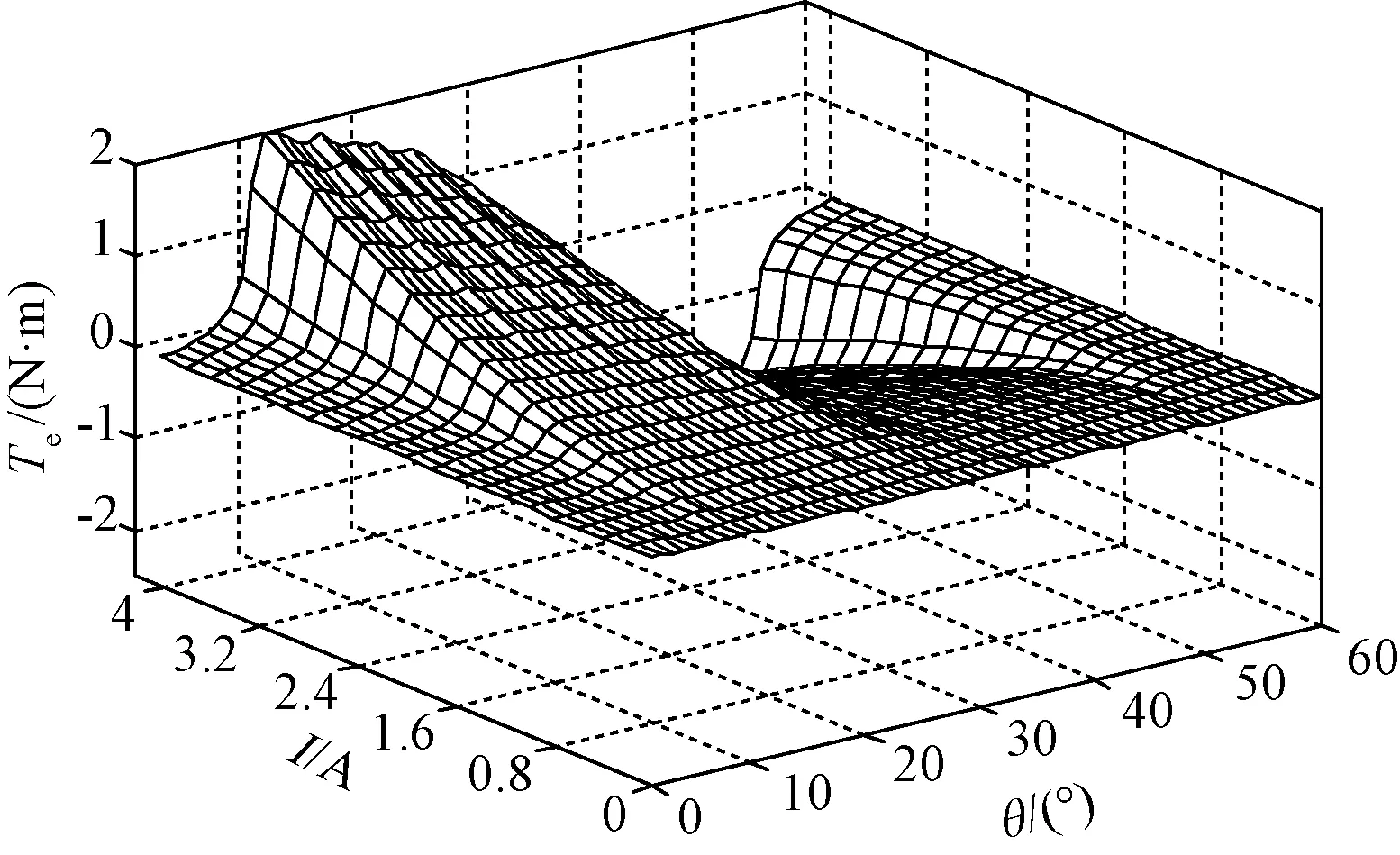
图3 根据实测结果绘制的转矩曲面模型Fig.3 Curved surface model of torque based on actual measurement results

图4为实测转矩和Maxwell3D计算的转矩误差图。可以看出，在转子磁极前沿和定子磁极前沿重合位置、转子磁极后沿和定子磁极后沿重合位置附近时，实测转矩和仿真转矩误差较大。这一方面是因为实际2°测量一次，精度较低；另一方面因为Maxwell计算转矩是建立在真空条件下的，而实际情况空气仍有一定的导磁率。

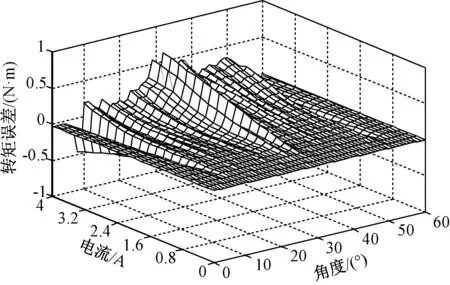
图4 转矩误差曲面Fig.4 Error surface of torque

虽然实测转矩和仿真转矩存在一定的误差，但基本可以确认仿真模型和仿真结果的准确性。实际应用中，通过多项式插值法将仿真出的转矩模型数据Te(i,θ)反演出转矩逆模型i(Te,θ)，如图5所示。实验中通过查表法获取当前所需转矩对应的电流值，采用电流闭环对转矩间接控制。

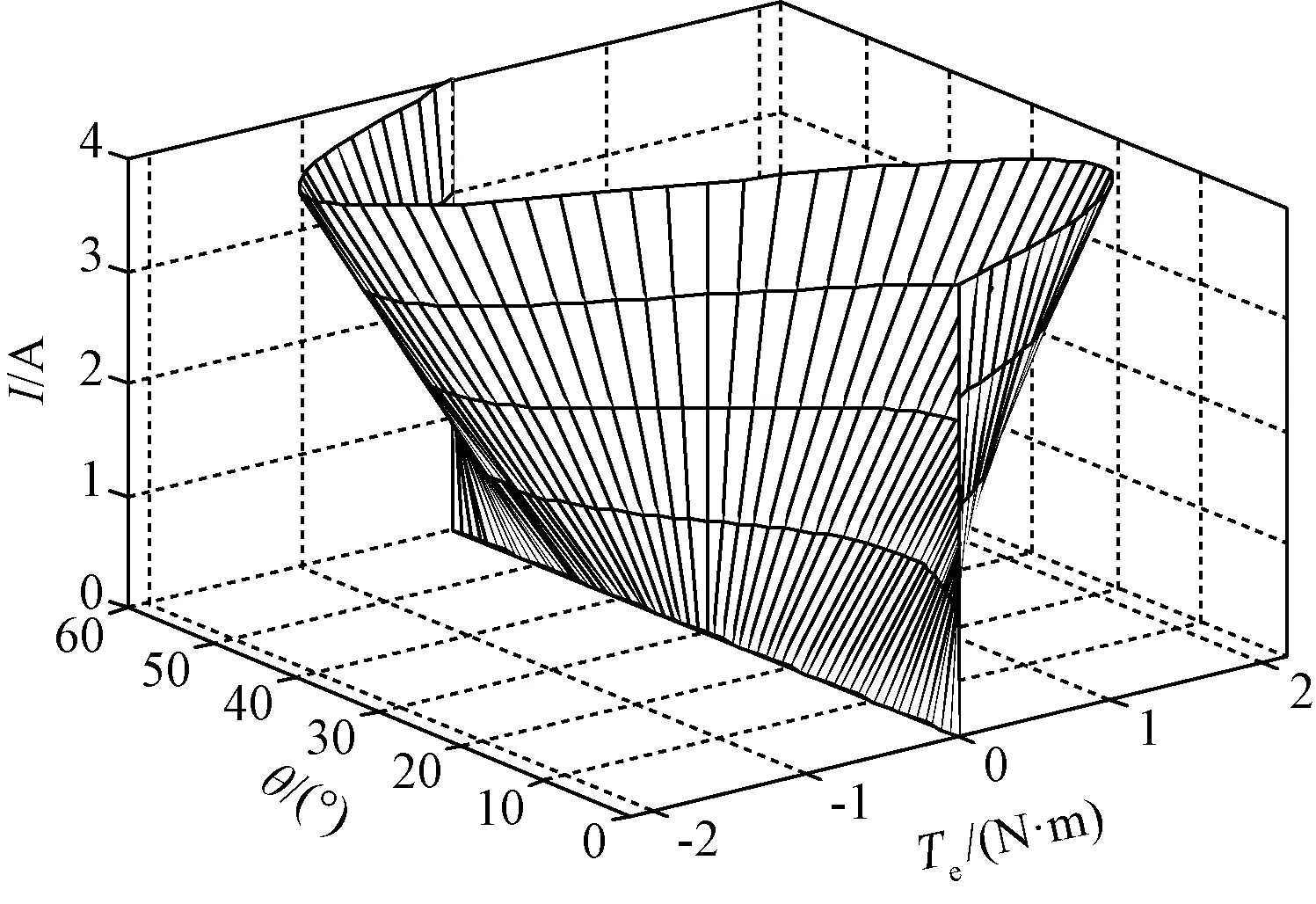
图5 转矩逆模型Fig.5 Inverse model of torque

3 转矩分配控制策略

对于三相及其以上的SRM，存在单相、两相以及两相以上通电方式，因此基于TSF的抑制转矩脉动的控制方法是为了使SRM在单相和多相导通时，合成瞬时转矩保持恒定，即利用TSF分配每相绕组在不同转角位置下的期望转矩，开通相的期望转矩按照一定规律上升，关断相的期望转矩按照一定规律下降。通过控制开通相的电流，使各相瞬时转矩跟随分配转矩，从而实现恒转矩输出。

TSF的不同直接影响SRM换相转矩脉动、馈电电压和相绕组铜耗，因而使SRM的效率和速度-转矩极限也受到一定程度的影响[8]。因此，合理地设置TSF对于提高SRM控制性能非常重要。TSF设计原则一般如下：任一时刻仅有一相绕组或相邻两相绕组通电，且各相绕组仅产生正转矩。

传统的TSF有直线型、余弦型、立方型和指数型等，如图6所示。其中θon为开通角；θoff不是传统控制方式(电流斩波和电压PWM)下的关断角，而是转矩按照TSF开始减小的起始位置角；θov为换相重叠角。

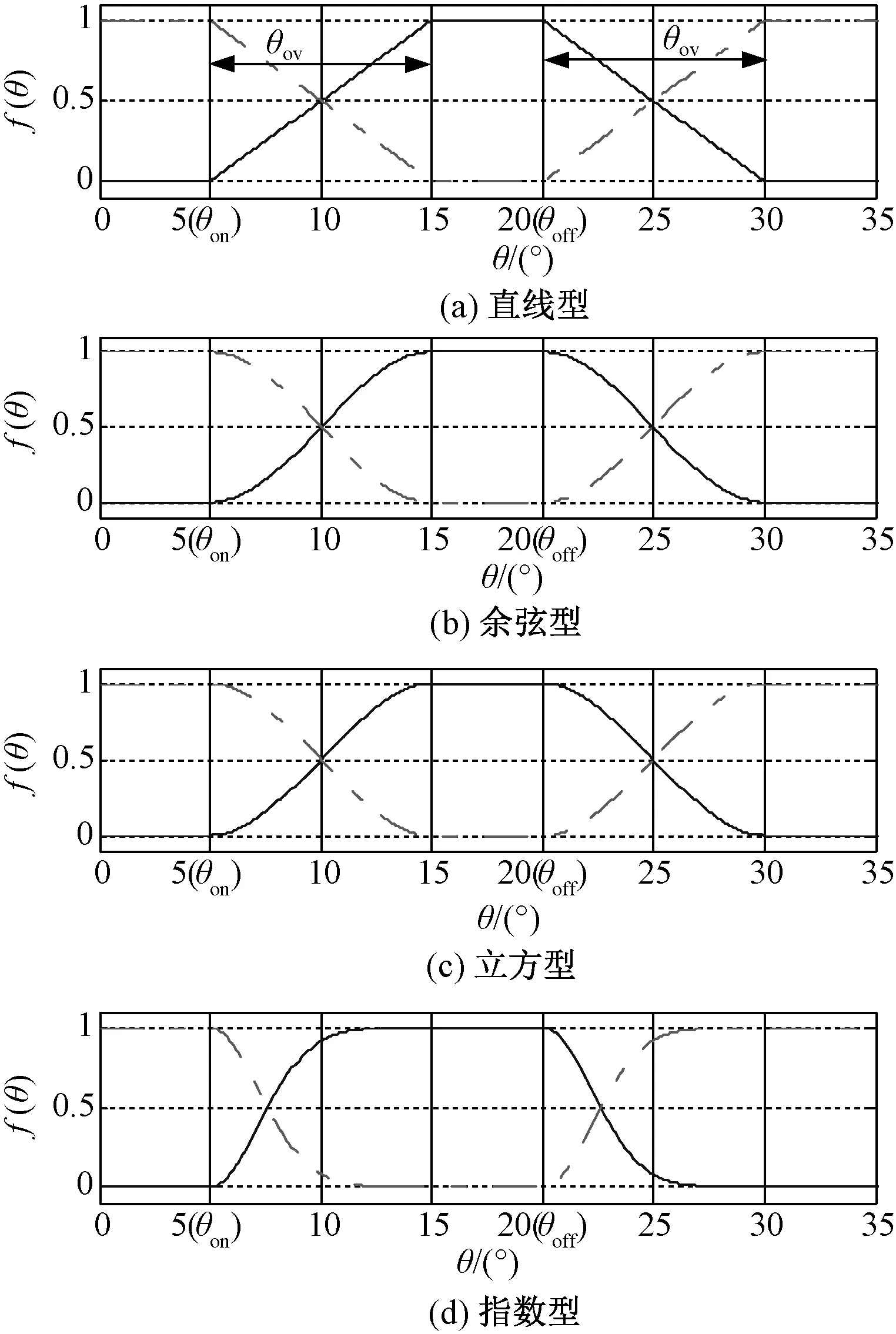
图6 传统的转矩分配函数Fig.6 Traditional torque sharing function

实际应用中受DSP计算速度的限制，只能选择直线型或立方型TSF。由于直线型对应的调速范围较小、铜耗较大[9]，故本文采用立方型TSF。在一个转子角周期60°内，导通相的立方型TSF为：

(1)

其中，换向重叠角θov、θoff和转子极距τ之间应满足约束条件：

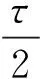
(2)

为了最大限度地扩展调速范围，同时在开通期间和关断期间不产生反向转矩，实验中将换向重叠角θov设置为7.5°，每个转子周期内每相绕组单独导通的角度也设置为7.5°，那么在一个转子角周期内，每相导通22.5°，开通角θon和θoff满足关系：

θoff-θon=15°

(3)

本文将开通角θon也设置为7.5°，一方面简化了软件编程，即每隔固定角7.5°产生一个开关信号；另一方面最大限度地减小了互感磁场和漏磁产生的影响，以A相为例，单个转子角周期内的三种导通状态如图7所示。如果开通角θon小于7.5°，那么在A相开通时刻，转子凸级更多地和B相磁极重叠，磁场走向趋向于经过B相和转子闭合，会产生反向制动转矩；如果开通角θon大于7.5°，那么根据式(3)可知，θoff大于22.5°，在高速情况下，A相电流会进入电感下降区，从而产生反向制动转矩。

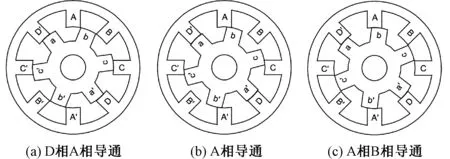
图7 单个转子角周期内A相的三种导通状态Fig.7 Three conduction states of phase A in a single rotor period

4 仿真与分析

本文以四相(8/6级)SRM为例建立SRM模型，其中，定子电阻Rs=0.1Ω，电源电压U=220V，转动惯量J=0.0017kg·m2，摩擦系数F=0.008N·m2，电感最大值Lmax=0.17H，电感最小值Lmin=0.0078H，电流为1～15A。给定转速600r/min，仿真中电机带1N·m负载起动，在0.2s时负载转矩突变为2N·m，0.3s时恢复为1N·m，仿真时长0.4s，系统结构框图如图8所示。

图8 系统结构框图Fig.8 System structure diagram

图9(a)为传统的电流斩波控制方式下的转矩波形，图9(b)为基于TSF的转矩间接控制方式下转矩波形。从图9可以看出，无论是起动、突加负载、突减负载还是稳态，基于TSF控制方式下的转矩脉动相对于传统斩波控制方式下的转矩脉动有明显的改善，转矩脉动小于给定转矩的10%，而传统方式下的转矩脉动远远大于给定转矩的20%，在起动和换相期间尤为明显。

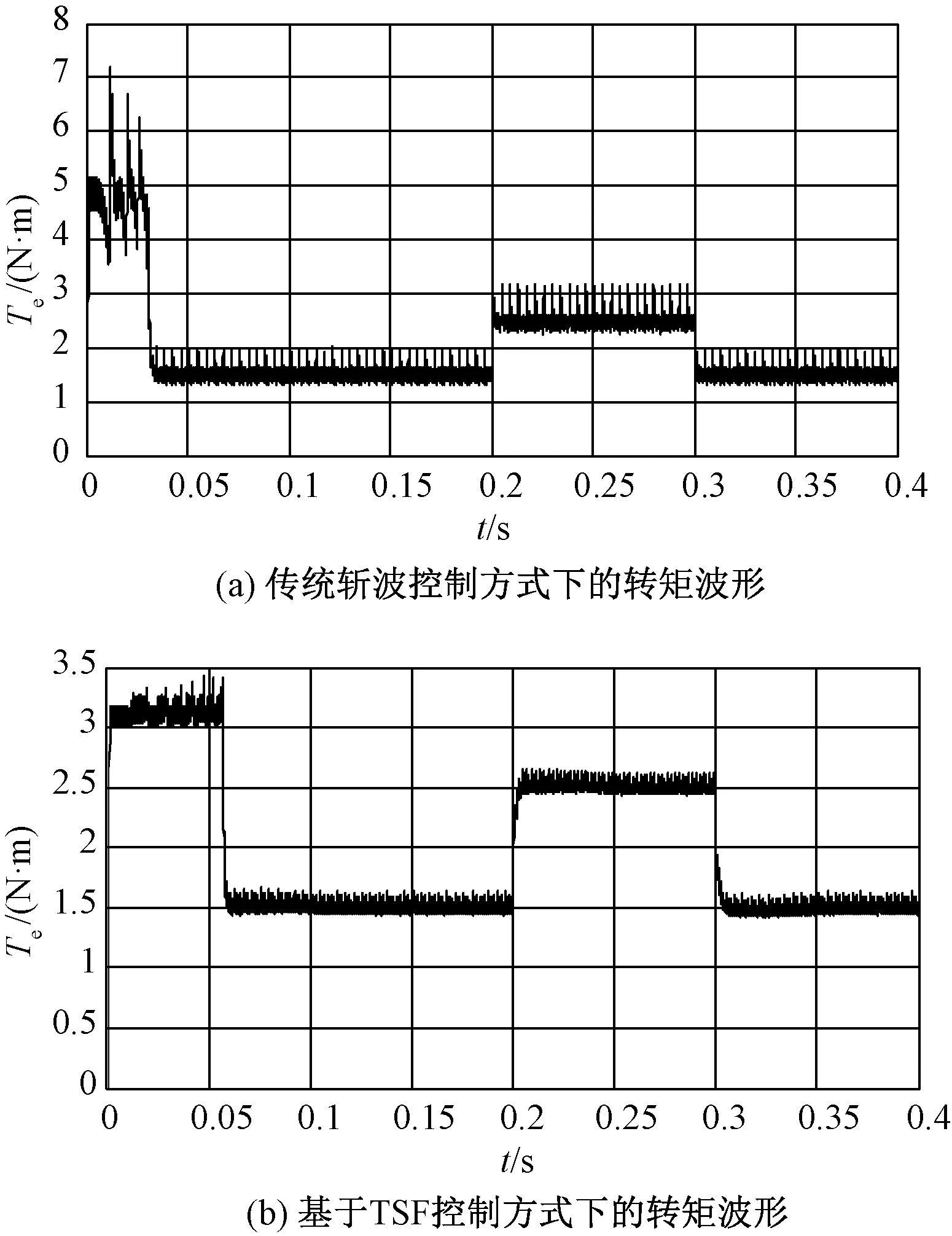
图9 转矩波形图Fig.9 Torque waveform

图10为当给定转速为600r/min时的转速响应曲线，纵坐标范围限制在590～610r/min。从图10可以看出，传统斩波控制方式下的稳态转速误差最高达到4r/min，突加负载或突减负载时，转速响应非常慢，且转速脉动随着负载转矩的升高而增大；本文基于TSF控制方式下的稳态转速误差几乎为0，突加负载和突减负载时，转速响应时间小于0.05s，且转速脉动基本为0。究其原因，一方面由于两种控制方式下的转速PID参数不同，另一方面由于控制对象不同，基于TSF控制方式是采用电流闭环对转矩进行间接控制，同时考虑了转矩和电流对转速的影响，而传统控制方式只是通过控制电流来调节转速，忽略了转矩对转速的影响。对比图9和图10可以看出，由于传统斩波控制方式下的瞬时转矩脉动较大，从而导致稳态时转速波动也较为明显。因此，通过抑制SRM的转矩脉动，可以使速度控制性能得到进一步的提升。

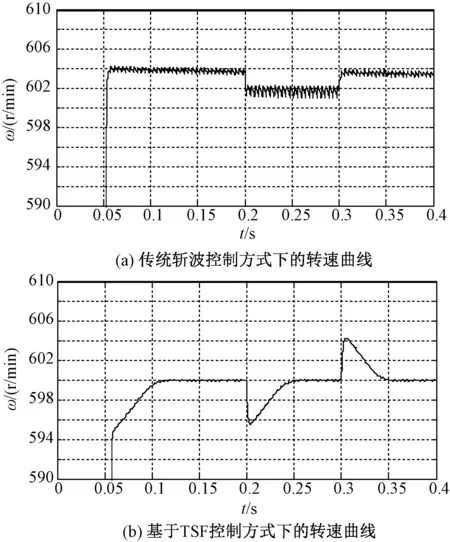
图10 转速响应曲线的局部放大图Fig.10 Partial enlarged drawing of speed response curve

5 实验与分析

实验电机为四相(8/6级)370W开关磁阻电动机，控制芯片采用TMS320F2812，编程软件采用CCS3.3，转矩、转速通过上位机CCS3.3软件自带的图形工具显示。静态扭矩传感器采用上海力恒LH-NJ-02。为了提高DSP的运行速度和计算精度，实验中使用了将浮点算法转换成固定点算法的IQmath库，故转矩和转速都以标幺值显示，其中转矩基值为2N·m，转速基值为2000r/min，给定转速为800r/min，即0.4pu。

图11为实验电机空载稳态(800r/min)下的转矩和转速曲线。从图11可以看出，在空载状态下，传统斩波控制方式的转矩波形很不平稳，波动范围较大，转矩脉动幅值约为0.44N·m；基于TSF控制方式的转矩波形相对较为平滑，转矩脉动幅值约为0.17N·m，远远小于前者。因此，即使在空载状态下，基于TSF控制策略相对于传统斩波控制方式的转矩脉动抑制效果就有了明显的改善。

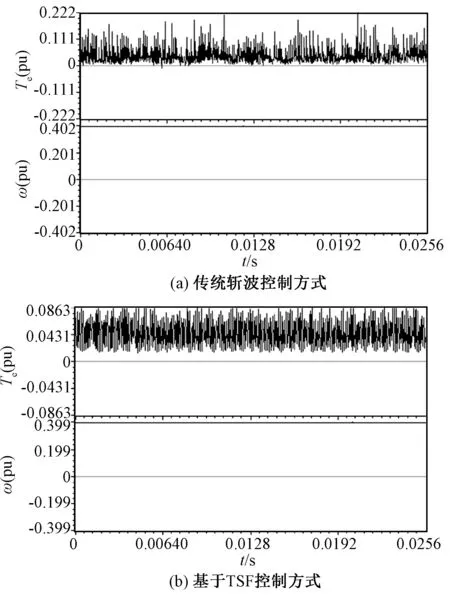
图11 空载稳态时的转矩和转速曲线Fig.11 Curves of torque and speed in no-load and steady state

图12为实验电机空载稳态下突加1N·m负载时的转矩和转速响应曲线。从图12可以看出，突加1N·m负载后，传统斩波控制方式下转矩脉动变大，脉动最大值达到0.25pu，即0.5N·m；基于TSF控制方式下的转矩脉动较小，脉动大小约为0.1pu，即0.2N·m。同时在突加负载时，传统斩波控制方式下的转速跌落了0.05pu，即100r/min；基于TSF控制方式下的转速跌落了0.35，即70r/min。由此可以看出，本文所述方法可以有效地抑制转矩脉动和提高速度控制性能。

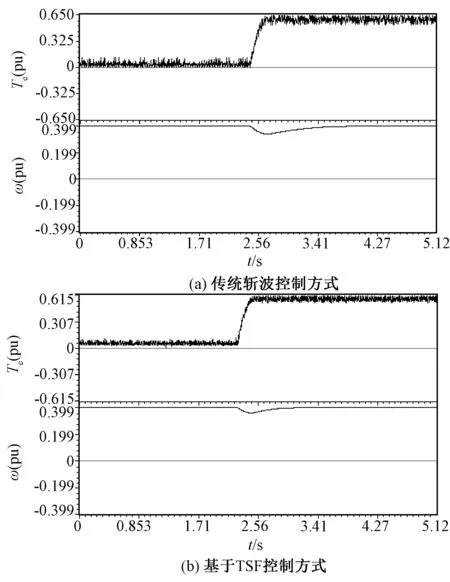
图12 突加负载时转矩和转速的响应曲线Fig.12 Response curves of torque and rotational speed under abrupt change of load

图13为基于TSF控制方式下，实验电机带1N·m负载、800r/min运行时的单相电流波形及其对应的开关管开关状态图。通道1为驱动信号波形，开关管的开通电压为+15V，关断电压为-5V；通道2为对应的电流波形，电流最大值为2.2A。

图13 带载、稳态下的电流波形Fig.13 Current waveforms under loaded and steady state

从图13可以看出，在每个转子周期内每相电流波形可以等分为三个状态，以A相为例，即DA相导通7.5°、A相导通7.5°和AB相导通7.5°三个状态，且在给定转矩下，三个状态所需的励磁电流逐渐下降。

6 结论

本文通过将实验电机建模，仿真出转矩模型，并将其和实测数据对比，验证了模型的准确性，为基于TSF控制方式的实验验证奠定了基础。通过合理地设置TSF的开通角、换向重叠角和关断角，有效地简化了程序设计，同时抑制了反向制动转矩的产生。仿真和实验采用基于TSF的电流闭环间接控制转矩的控制方式，其结果验证了本文所述控制方式可以有效地抑制转矩脉动，也说明了转矩脉动的抑制可以有效地提高速度控制性能，同时也为SRM转矩脉动抑制的研究和实验验证提供了新思路。

[1] 孙丹,贺益康,智大为,等 (Sun Dan, He Yikang, Zhi Dawei, et al.). 基于非线性模型的开关磁阻电机自适应模糊控制(Development of dynamic testing device for electromagnetic apparatus with opto-electromechanical technology) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2001, 20(4): 9-13.

[2] 王宏华 (Wang Honghua). 开关磁阻电动机调速控制技 术(The speed regulation and control technology of switched reluctance motor) [M]. 北京: 机械工业出版社 (Beijing: China Machine Press), 2011.

[3] 陈小元，彭亦稰(Chen Xiaoyuan, Peng Yixu). 基于电流补偿策略的转矩分配函数法抑制整距绕组分块转子SRM的转矩脉动(Torque-ripple minimization for SRMs with segmental rotors and fully-picthed windings based on TSF by current compensation strategy) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2014, 29(1): 72-76.

[4] 夏长亮，陈自然，李斌，等 (Xia Changliang, Chen Ziran, Li Bin, et al.). 基于RBF神经网络的开关磁阻电机瞬时转矩控制(Instantaneous torque control of switched reluctance motors based on RBF neural network) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2006,26(29):127-132.

[5] 蒋湘君 (Jiang Xiangjun). 基于转矩分配的开关磁阻电 机转矩脉动抑制的研究 (Research of switched reluctance motor torque ripple suppression based on torque distribution) [D]. 长沙：中南大学(Changsha: Central South University), 2014.

[6] 曹家勇, 周祖德, 陈幼平，等 (Cao Jiayong, Zhou Zude, Chen Youping, et al.). 一种开关磁阻电动机转矩控制的新方法(A new torque control method for switch reluctance motor) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2005,25(6): 88-94.

[7] 刘涛, 吴忠, 吕昊暾 (Liu Tao, Wu Zhong, Lv Haotun). 开关磁阻电动机转矩分配策略研究 (Torque control in switched reluctance motor using a torque allocation function) [J]. 微电机(Micro motor), 2013, 46(7): 63-67.

[8] Ilic-Spong M, Miller T J E, Macminn S R, et al. Instantaneous torque control of electric motor drive [J]. IEEE Transactions on Power Electronics, 1987,2(1):55-61.

[9] Xue X D, Cheng K W E, Ho S L. Optimization and evaluation of torque-sharing functions for torque ripple minization in switched reluctance motor drives [J]. IEEE Transactions on Power Electronics, 2009, 24(9):2076-2090.

TorquerippleminimizationforswitchedreluctancemotorbasedonTSF

YANG Guang， YANG Ming-fa， SHI Kai

(College of Electrical & Automation Engineering, Fuzhou University, Fuzhou 350116, China)

Instantaneous torque ripple is one of the important difficulties of the switched reluctance motor to be solved, which limits the performance of speed control and position measurement precision for the further enhancement. The theoretical study of SRM torque ripple suppression based on torque distribution has made great progress, but the torque is difficult to be accurately fed back in practical application because of the nonlinear magnetic circuit. According to the actual specification and size of the motor, this paper calculates the torque under the different rotor position and phase current by using the software of Maxwell3D, then torque-current inverse model is set up. It simplifies the programming and inhibits the braking torque by reasonably setting the turn-on angle, commutation overlap angle and turn-off angle. The torque is controlled by adjusting the phase current based on the torque sharing function in the simulation and experiment, and the results show that the method can effectively reduce the torque ripple.

switched reluctance motor (SRM)； torque ripple minimization； torque model； torque sharing function (TSF)

2016-08-15

杨 光(1991-), 男, 河南籍, 硕士研究生, 研究方向为电力电子与电力传动；杨明发(1977-), 男, 福建籍, 副教授, 博士, 研究方向为电机电器及其系统智能化与在线监测技术(通讯作者)。

10.12067/ATEEE1608028

1003-3076(2017)12-0008-07

TM352