随环境条件变化的输电线路输送容量概率建模研究

张 斌， 林章岁， 叶 荣， 胡臻达， 金 涛， 温步瀛

(1. 福州大学电气工程与自动化学院， 福建 福州 350108；2. 国网福建省电力有限公司经济技术研究院， 福建 福州 350003)

随环境条件变化的输电线路输送容量概率建模研究

张 斌1， 林章岁2， 叶 荣2， 胡臻达2， 金 涛1， 温步瀛1

(1. 福州大学电气工程与自动化学院， 福建 福州 350108；2. 国网福建省电力有限公司经济技术研究院， 福建 福州 350003)

充分挖掘线路的输电潜能，提高现有电网的输电效率，是当前研究的一个热点。通常输电线路中静态载流量的计算是在保守的环境下获得，未考虑到实际运行环境。而动态载流量的计算是通过对运行环境的实时监测值，即结合实际环境温度、风速等因素，来确定其传输的极限容量，由此可以提高线路的输电效率。本文通过BP神经网络对某地区的历史气象数据进行分析和预测，由于该方法对气象预测效果较好，故将预测获得的数据作为概率模型的源数据，并提出一种基于电流密度函数的概率建模的动态增容研究方法。通过动态增容方法在某地区的应用分析，表明在迎峰度夏时可适当提高输电线路载流量，且可确保输电线路的供电可靠性。

输电能力；动态载流量；BP神经网络；概率建模；动态增容

1 引言

随着社会经济的发展和人们用电水平不断增加，电网的输电能力呈现不足。大部分输电线路受到载流量热稳定限额的制约[1]，远远不能满足电网的实际需要。在电力市场运行的环境下，电网的输电能力也是一种市场信号，其输电能力反映在输送容量上，各运营中的电网都希望尽可能地多输出容量。

20世纪70年代，美国电力研究学者M. W. Davis针对电力传输线提出动态热定值这一概念[2,3]，随后在80年代，美国电力研究院(EPRI)针对电力输送过程提出了采用电量参数测定设备结合气象监测系统对电力线路进行容量实时监控的思想，设计出DTCR检测系统[4,5]，随后这一系统被SRP公司应用在两条大容量输电线路上，使线路容量大幅度提升，延缓5年建设新的线路，节省了大量费用。

近年来国内也开始重视动态增容技术。文献[6]提出电热耦合的潮流模型，实时把握电网潮流与输电元件温度间变化的关系，以达到在各种情况下由输电元件温度决定其输送能力的目的；文献[7]提出了对架空输电线路实施实时监测并结合相关的数学模型计算线路的热载流量，从而最大限度地发挥线路的输送能力；文献[8]提出一种对超高压输电线路进行动态增容研究的方法，即将静态增容和动态增容的两个方法结合起来，使增容效果更明显；文献[9]提出了一种基于状态估计的实时载流计算方法，主要考虑线路的热稳定制约、电压制约、功角稳定制约三种因素；文献[10]对载流量算法进行改进，减小了载流量的波动，并增加了动态增容技术的实用性；文献[11]基于Bayes时间序列统计方法，根据实时运行状态的数据进行输电容量的概率故障预测和风险评估，但该方法是在低质量数据上进行粗略的检验，精度不足。

本文提出的方法不增加输电线路实时在线监测设备的数量，基于BP神经网络对历史气象数据进行统计并预测，将预测结果用于热平衡方程，对输电线路载流量进行概率分析。

2 理论分析

2.1 载流量的计算

导线处于最高允许温度工作状态下，若其电流能使线路吸热与散热达到平衡，此时的电流值即为最大允许载流量。最大允许载流量的计算有多种方案，常见的有IEEE 2006-738标准、《110kV～750kV架空输电线路设计规范》、摩根公式[12]。其计算的原理都来源于热平衡方程：

I2R(TC)+WS=WR+WF

(1)

式中，WS为日照吸热功率；WR为辐射散热功率；WF为对流散热功率；TC为导线温度；R(TC)为温度TC时导线交流电阻；I为导线载流量。由式(1)可推导出导线载流量的计算公式为：

(2)

本文采用IEEE标准计算载流量，其基本公式仍为热平衡方程。

(1)辐射散热公式WR为：

(3)

式中，D为导线直径；ε为导线辐射散热系数，取值区间为[0.9,0.95]；ta、tp分别为导线环境温度和最大允许温度。

(2)对流散热功率WF为：

(4)

式中，vw为风速；ρ为空气密度，其值为：

(5)

其中，He为导线高度；HC为太阳高度角，其值为：

HC=arcsin[cosLatcosδcosω+sinLatsinδ]

(6)

其中，δ为太阳倾斜角；Lat为导线所处的维度；ω为小时角，其值为与中午 12∶00 相差的小时数乘以 15°。μ为空气动态粘度，其值为：

(7)

kf为空气热传导率，其值为：

(8)

ka为风向因子，其值为：

(9)

其中，φ为风与导线轴向的夹角。由于风速大于零，且本文研究的是垂直于导线的风速，即φ=90°，故ka值为1。

(3)日照吸热功率WS为：

WS=αKSQSDsinθ

(10)

式中，α为导体对光照的吸收率；QS为单位面积的光照热量，其值为：

(11)

其中，系数A～G取决于环境的清洁程度。

θ为太阳光入射有效角，其值为：

θ=C+arccos[cosHCcos(ZC-ZL)]

(12)

其中，ZC为太阳方向角；ZL为线路方位角。

KS为热量高度修正因子，其值为：

(13)

(4)交流电阻值为：

(14)

式中，R(Thigh)为温度为Thigh时的导线交流电阻；R(Tlow)为温度为Tlow时的导线交流电阻。由经验值可得，当选取Thigh为75℃、Tlow为25℃温度下导线的电阻值与实际的电阻值之间的误差是可以忽略的。

2.2 基于BP神经网络的天气预测

2.2.1 BP神经网络的原理

在机器学习和认知科学中，人工神经网络(ANNs)专门指由生物神经系统启发的统计学习的数学模型。人工神经元模型如图1所示。

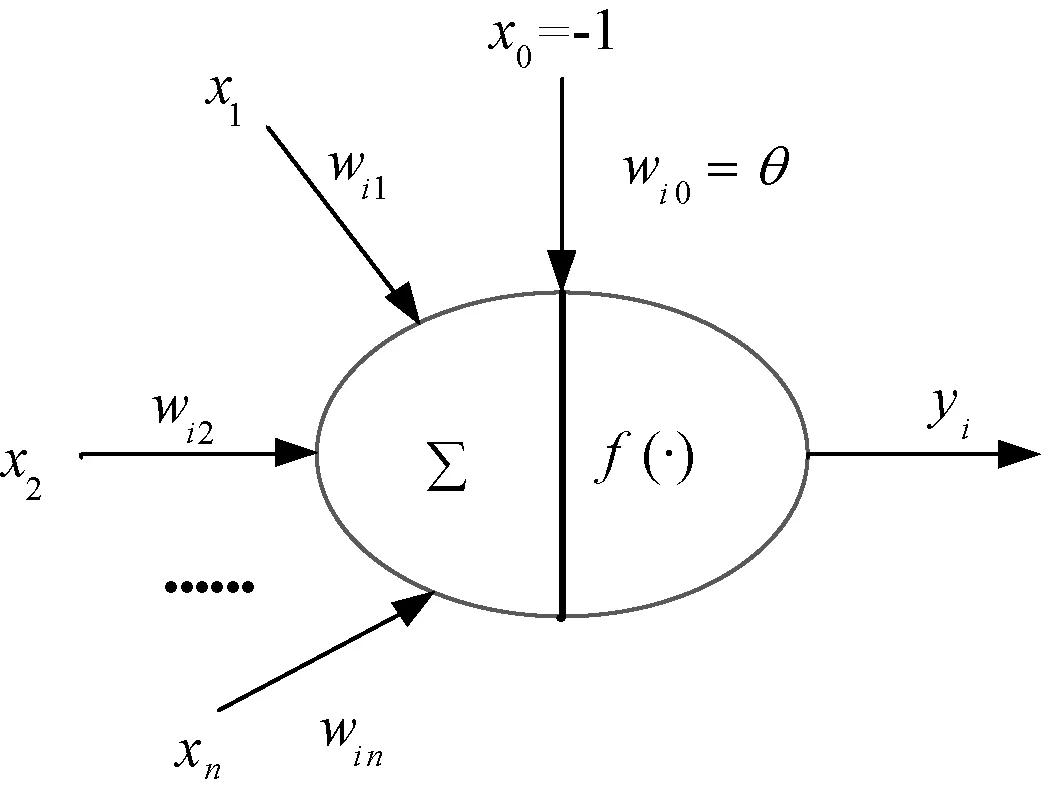
图1 人工神经元模型 Fig.1 Artificial neuron model

神经元n维的输入为x0,x1,x2,… ,xn，用列向量表示如下：

X=[x0,x1,x2,…,xn]T

(15)

神经元输出用yi来表示； 各神经网络之间的连接权值为wi0,wi1,wi2, …,win，用列向量表示如下：

W=[wi0,wi1,wi2, ...,win]T

(16)

θ为神经元的阈值，当输入的信号和超过θ时，就可激活神经元；net为输入信号加权求和值，即

(17)

输出值yi表示如下：

yi=f(net)=f(XW)

(18)

BP神经网络可以对输入、输出之间的非线性函数关系进行反映，因此无需过分依赖数学模型，并且在连接权值中输入一旦出现部分神经元损坏的现象也不会导致大面积连接权值的改变，因此对系统整体输入输出影响较小，使得BP神经网络具有十分强大的容错能力。另外BP网络还具有灵活性超强的网络拓扑(如图2所示)。在气候预测上，神经网络有很广泛的应用，它可以利用历史天气的气象特征，以及对应的数据进行网络的训练，从而达到预测天气的目的。

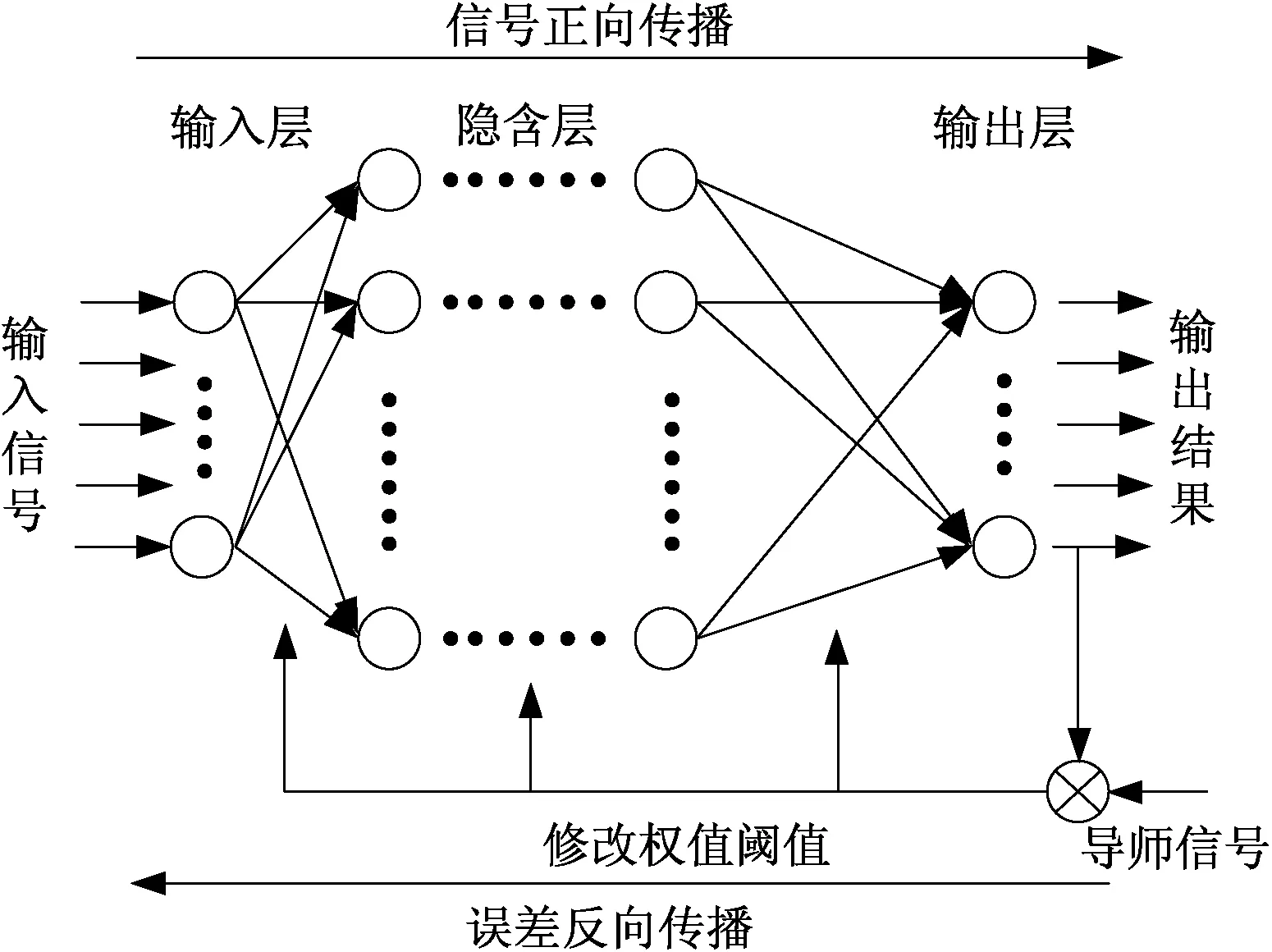
图2 BP神经网络的拓扑结构Fig.2 Topological structure of BP neural network

图2中，BP神经网络学习过程包括信息的正向传播过程和误差信息的反向传播。信息在BP神经网络的正向传播过程中，输入信号经过多个隐含层传输至输出层，则输出值要和期望值进行对比，若期望值与输出结果之间存在超出接受范围的误差，则通过误差的反向传输过程对权值系数进行修正，尽量缩减输出信号与期望值的误差。信息输入、输出对应关系如图3所示。

图3 BP神经网络训练流程图Fig.3 BP neural network training flow chart

2.2.2 预测模型的建立

以某地区逐日环境温度和风速为例。首先统计近几年的环境温度和风速数据，然后利用BP神经网络完成预测模型的构建，同时为了确保所建模型相对独立，建模的数据样本选取近几年[13]，故预测对象可为环境温度和风速。由于能够预测未来某段时间的环境温度和风速，该模型可以很好地用于气候条件的预测，同时能减少在线监测设备的数量，降低成本。

在建立的预测模型中，输入为环境温度和风速的时间序列，输出为环境温度和风速值。该模型中有一个输入层节点，两层隐含层且每层有10个节点，输出层1个节点，学习率、训练次数分别设置为0.001和10000次。

2.2.3 预测效果分析

采用Matlab工具对所建立模型进行训练、测试和检验。采用动量梯度的下降算法有利于检验，使拟合精度和预测精度更高。表1为训练10000次后的收敛和拟合情况。可以看出，该模型对环境温度和风速的预测拟合效果比较理想。其预测的时间尺度是以天为单位，预测出来的数据作为概率模型求解的源数据。

表1 2011～2015年某地区预测的收敛和拟合情况Tab.1 Convergence and fitting of a region forecast from 2011 to 2015

3 概率模型计算与分析

3.1 概率模型的建立

在气象要素中，温度遵从正态分布[14]，其正态分布密度函数如式(19)所示；风速服从威布尔分布[15]，其威布尔密度函数如式(20)所示。由2.2.1节BP神经网络预测的数据样本，拟合可得参数μ=25.8695,σ=8.7995,a=6.6494,b=11.6480。在Matlab实验环境中，结合热平衡方程和载流量计算式(2)，可画出环境温度、风速和电流的关系，如图4～图6所示。

(19)

(20)

图4 环境温度对电流变化的影响Fig.4 Influence of ambient temperature on current variation

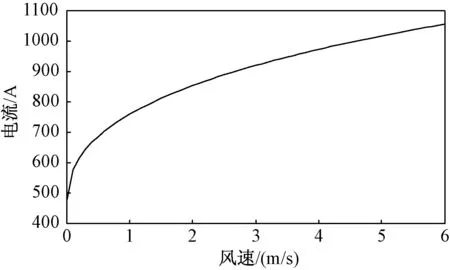
图5 风速对电流变化的影响Fig.5 Effect of wind speed on current variation

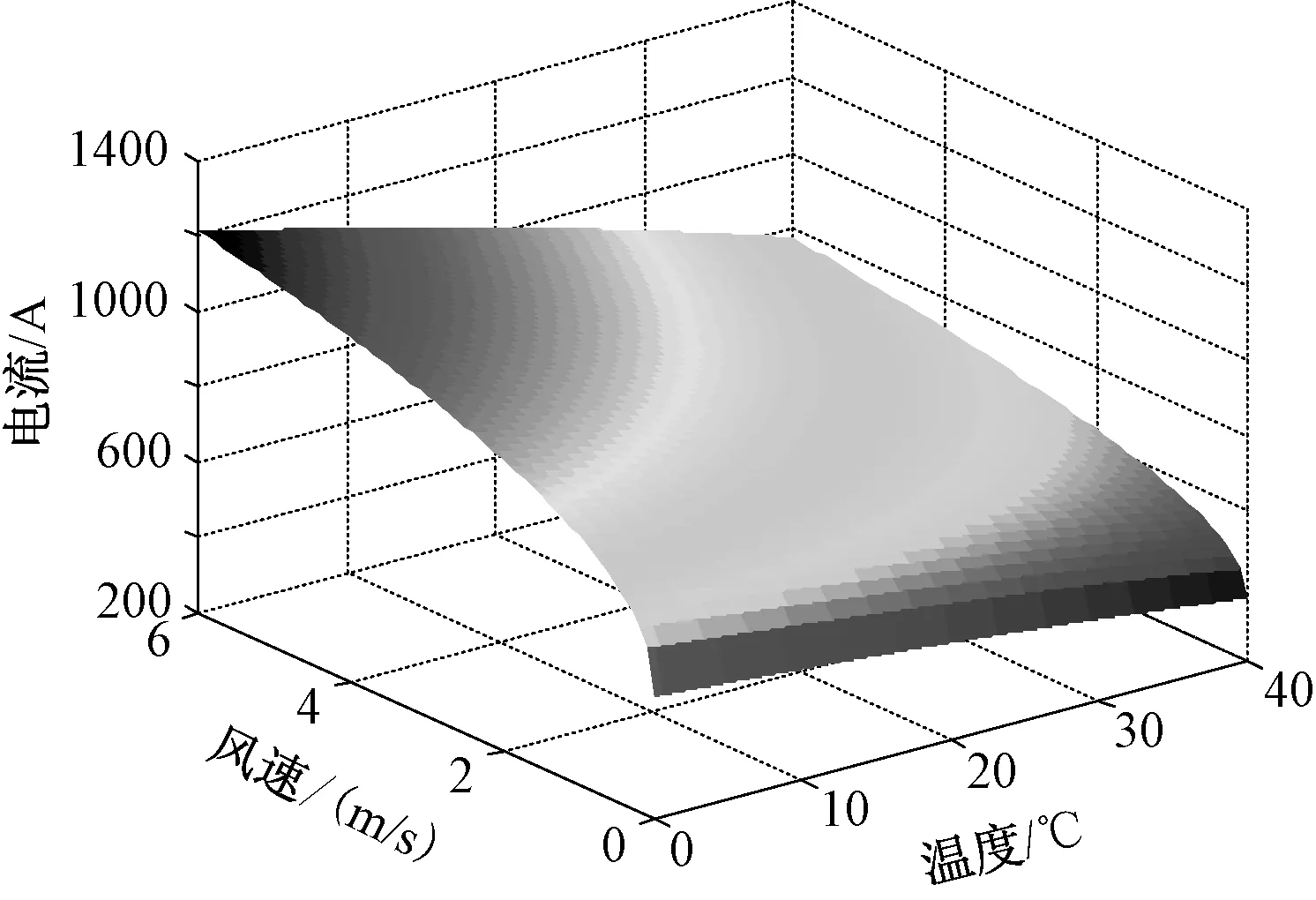
图6 环境温度和风速对电流变化的影响Fig.6 Ambient temperature and wind speed on current changes

由图4可以看出，环境温度升高会使线路载流能力下降，但是同时用户用电需求量更大，所以在夏季需要采取相应的增容措施。由图5可以看出，随着风速的增加，导线散热加快，使得线路载流能力升高。由图6可以看出，在风速较大和环境温度适中的条件下，输电线路载流量较大。

以LGJ400/25导线为例，根据式(2)，在已知环境温度和风速分布函数条件下，可画出载流量全天24h的概率密度分布，如图7所示。

图7 载流量概率密度函数Fig. 7 Current probability density function

根据该地区气候具体情况，在春夏秋冬四个季节中各选2个典型工况，并计算其电流，结果如表2所示。由图7的电流概率密度函数，并通过三次样条插值的方法获得更加密集的点，然后通过积分得到表2对应的区间概率，如表3所示。由表2可以看出，在同为5m/s风速状态下，环境温度越高，线路的输电容量越低；对于环境温度同样为22℃的输电线路，风速越高对应越高的线路容量；相对于春天，冬天的风速较高且环境温度较低，输电线路容量也较高，这与实际情况相吻合。

表2 典型工况的电流值Tab.2 Typical operating conditions of current value

表3 电流区间概率值Tab.3 Current range probability values

3.2 概率模型的误差分析

在概率模型建立过程中，误差的来源主要是环境温度和风速的预测。从第2节中基于BP神经网络对环境温度和风速的预测可以看出，预测效果较好，但仍然存在误差，故会给电流密度函数的概率建模带来一定的误差。在BP神经网络中，采用测试数据来监测预测的效果，然后将某年份夏季40天预测的气象数据和真实的气象数据代入载流量计算公式(2)中，画出载流量误差率，如图8～图10所示。

图8 环境温度对载流量误差率变化的影响Fig.8 Ambient temperature on impact of changes in carrier current error rate

图9 风速对载流量误差率变化的影响Fig.9 Wind speed on impact of changes in carrier current error rate

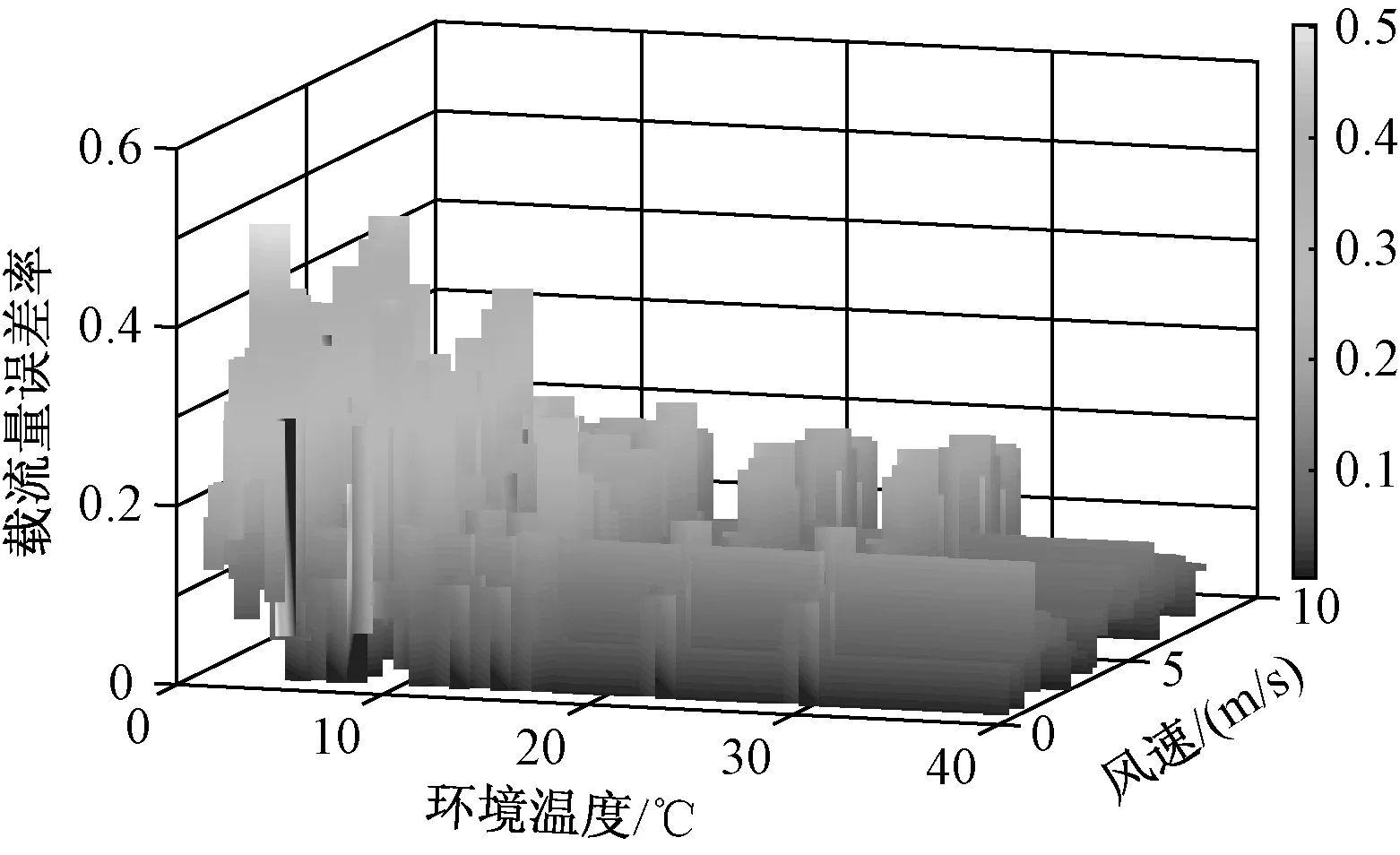
图10 环境温度和风速对载流量误差率变化的影响Fig.10 Influence of ambient temperature and wind speed on variation of carrier current error rate

图8中，环境温度的预测误差对载流量的误差率波动范围为[0.009,0.118],误差率均方根为0.049；图9中，风速预测误差对载流量的误差率波动范围为[0.091,0.187]，误差率均方根为0.134；图10中，环境温度和风速预测误差引起载流量误差率波动范围为[0.002,0.502],误差率均方根为0.094，且环境温度在4℃～10℃和12℃～14℃预测范围对载流量误差率影响较大，而风速在4～6 m/s预测范围引起载流量误差率也相对大些。从图8和图9计算的误差率均方根可以看出，基于BP神经网络对环境温度和风速的预测误差引起的载流量误差在可接受的范围内。

4 算例分析

根据第2和第3节的模型及其相应的公式，利用Matlab软件编写载流量计算程序分析动态增容在该地区110kV输电线路的实际应用情况。计算中，根据气象监测中心的实时微气象数据，导线最大允许运行温度设为70℃，结合热平衡方程对线路的每天最大允许载流量进行计算，所得结果和线路实际载流量进行比较并分析。表4为10天最大允许载流量计算值、监测的实际载流量的统计情况。

表4 动态允许载流量计算Tab.4 Dynamic allowable ampacity calculation

由表4中可以看出，导线实际运行的载流量有很大提升空间，从这10组数据比较可得，最大允许载流量的最小值也达813.8A，比该10组中实际运行的载流量最大值(502.9A)及原限额(600A)都有显著提高。由此可见，采用实时动态增容技术可有效挖掘线路的输电潜能，在用电高峰期可适当提高输送容量，缓解用电紧张。

2013年8月1日～8月31日期间，采用该模型对该地区某风电场的输电容量进行分析，且对环境温度、风速、实际运行载流和安全载流限额进行统计与计算，结果如图11～图13所示。

图11 环境温度曲线Fig.11 Ambient temperature curve

图12 风速曲线Fig.12 Wind speed curve

图13 动态增容情况曲线Fig.13 Dynamic capacity increase curve

图11和图12为某地区夏季高温月的环境温度和风速的变化曲线图。图13中，在近一个月的时间段里，根据SCADA系统采集的电流数据，在8月21日0∶00时，出现导线最大的实际载流值，为502.9A。动态增容的电流安全限额比原限额600A大很多，且在8月4日达到最低计算值766.4A，相比与原限额增加了166.4A，约提高了28%。由表3可知，电流区间在750～900A的概率值最大，为0.5693，而电流区间在750～1050A的概率值达到0.9548。当图7中的电流概率密度值处于峰值时，电流值为886.2A,即其值出现的频率是最高的，所以在夏季，当企业和居民家里开始使用空调等制冷设备时，用电需求量大大增加，输电线路的输送容量可适当提高限额至886.2A，以满足用电高峰期用电量的需求。

5 结论

本文通过BP神经网络对某地区的历史气象数据进行统计并拟合回归，由于对环境温度和风速拟合效果较好，所以采用该网络对该地区的环境温度和风速进行一段时间的预测来获得一系列预测数据样本。然后用预测数据样本对环境温度和风速的分布函数中的参数进行拟合，同时结合热平衡方程和IEEE2006-738载流量计算公式，计算出四季典型工况下的载流量和画出电流概率密度函数图。从载流量的分析结果可知，环境温度越高，输电线路的载流能力呈下降趋势；风速越高，对导线散热作用越快，故线路的载流能力会有所升高。从电流概率密度函数可以看出，电流在750～900A范围的概率较大，故输送载流量可适当提高到886.2A。为了迎峰度夏，夏季采取一定增容措施是很有必要的。

[1] 彭向阳，周华敏，郑晓光，等(Peng Xiangyang, Zhou Huamin, Zheng Xiaoguang, et al.).提高广东架空送电线路输送容量研究(Study on raising transmission capacity of overhead transmission line in Guangdong power grid)[J]. 南方电网技术(Southern Power System Technology), 2009, 3(6):77-81.

[2] Davis M W. A new thermal rating approach: The real time thermal rating system for strategic overhead conductor transmission lines - Part I [J]. IEEE Transactions on Power Apparatus and Systems, 1977, 96(3): 803-809.

[3] Davis M W. A new thermal rating approach: The real time thermal rating system for strategic overhead conductor transmission lines - Part II [J]. IEEE Transactions on Power Apparatus and Systems, 1977, 96(3): 810-825.

[4] Douglass D A, Edris A. Field studies of dynamic thermal rating methods for overhead lines[A]. IEEE Transmission and Distribution Conference [C]. 1999. 2: 842-851.

[5] Douglass D A, Lawry D C, Edris A A, et al. Dynamic thermal ratings realize circuit load limits[J]. IEEE Computer Applications in Power, 2000, 13(1): 38-44.

[6] 丁希亮，韩学山，张辉，等(Ding Xiliang, Han Xue-shan, Zhang Hui, et al.). 电热协调潮流及输电线路温度的变化过程分析(Analysis on electrothermal coordination power flow and transmission line temperature variation process)[J]. 中国电机工程学报(Proceedings of the CSEE), 2008, 28(19):138-144.

[7] 李莉华，高翔(Li Lihua, Gao Xiang). 大截面导线技术(Large cross section conductor technology for power transmission)[J]. 上海电力(Shanghai Electric Power), 2007, (6):590-593.

[8] 吉兴全，杜彦镔，李可军，等(Ji Xingquan, Du Yanbin, Li Kejun, et al.). 一种超高压输电线路动态增容方法(A method of dynamic rating of ultra high voltage transmission line)[J]. 电力系统保护与控制(Power System Protection and Control), 2015,43 (3):102-106.

[9] 梁立凯，韩学山，王艳玲，等(Liang Likai, Han Xueshan, Wang Yanling, et al.). 输电线路载荷能力在线定值(Online valuation of transmission line load ability)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2013, 28(2):279-284.

[10] 李天助，汪沨，牛雪松，等(Li Tianzhu, Wang Feng, Niu Xuesong, et al.).架空导线动态载流量的分析及改进算法(Analysis of dynamic carrying capacity of overhead conductor and its improved algorithm)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2016, 35(11):59-64.

[11] 朱文俊，刘文山，彭向阳，等(Zhu Wenjun, Liu Wenshan, Peng Xiangyang, et al.). 提高输电线路输送容量的短期风险评估(Short-term risk assessment of dynamic line rating)[J]. 广东电力(Guangdong Electric Power), 2010, 23(3): 7-11.

[12] 韩晓燕，黄新波，赵小惠，等(Han Xiaoyan, Huang Xinbo, Zhao Xiaohui, et al.). 输电线路摩尔根载流量简化公式的初步研究(Preliminary study on morgan transmission capacity simplified formula of transmission lines)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2009, 21(5):92-96.

[13] 福清历史天气(Historical weather of Fuqing)[EB/OL]. http://lishi.tianqi.com, 2016-01-07.

[14] 黄嘉佑，李庆祥(Huang Jiayou, Li Qingxiang). 气象数据统计分析方法(Meteorological data statistical analysis method)[M].北京：气象出版社(Beijing: China Meteorological Press), 2014.

[15] 李慧, 孙宏斌, 张芳,等(Li Hui, Sun Hongbin, Zhang Fang, et al.).风电场风速分布模型研究综述(Summarization on wind speed distribution model of wind farm)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(8):62-66.

Probabilisticmodelingoftransmissioncapacityoftransmissionlineswithchangingenvironmentalconditions

ZHANG Bin1, LIN Zhang-sui2, YE Rong2, HU Zhen-da2, JIN Tao1, WEN Bu-ying1

(1. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108，China;2. Economic and Technological Research Institute, State Grid Fujian Electric Power Co. Ltd., Fuzhou 350003, China)

How to calculate the transmission capacity of the transmission lines, fully extend the transmission potential of lines and improve the transmission efficiency of the existing power grid is a focus of the current research. Usually current-carrying capacity of transmission lines is obtained in conservative weather conditions. The actual operating environment is not taken into consideration. The calculation of dynamic-carrying capacity is made through the real-time monitoring of operating environment, including the actual environment temperature, wind speed and other factors. Then the ultimate capacity of the transmission is determined, which greatly improves the power transmission efficiency of lines. In this paper, the historical meteorological data of a certain area are fitted and forecast by BP neural network in the experimental environment of Matlab. Because weather at the network is better forecast, the data obtained from the forecast is the source of the probability model. And a research method of dynamic capacity increase based on the probability model of the current density function is proposed. The application of dynamic capacity increase in this area can be analyzed: At the peak or in the summer, transmission lines can be appropriately increased to 800A, and the reliability of power supply for transmission lines can be ensured.

transmission capacity; dynamic-carrying capacity; BP neural network; probabilistic modeling; dynamic capacity-increase

2016-11-21

福建省自然科学基金项目(2013J01176)

张 斌(1992-)， 男， 福建籍， 硕士研究生， 研究方向为输电线路的动态增容分析；林章岁(1964-), 男， 福建籍， 高级工程师， 硕士， 研究方向为电网规划设计及管理。

10.12067/ATEEE1611047

1003-3076(2017)12-0046-07

TM751