基于PSO-OMP优化的WD-ASD超短期负荷预测

曲正伟， 张 坤， 王云静， 韩艳丰， 郝丽丽， 王崇轶

(1. 电力电子节能与传动控制河北省重点实验室， 燕山大学， 河北 秦皇岛 066004； 2. 华北电力大学电气与电子工程学院， 河北 保定 071003； 3. 北京亦庄国际开发建设有限公司， 北京 100176)

基于PSO-OMP优化的WD-ASD超短期负荷预测

曲正伟1， 张 坤1， 王云静1， 韩艳丰1， 郝丽丽2， 王崇轶3

(1. 电力电子节能与传动控制河北省重点实验室， 燕山大学， 河北 秦皇岛 066004； 2. 华北电力大学电气与电子工程学院， 河北 保定 071003； 3. 北京亦庄国际开发建设有限公司， 北京 100176)

为提高负荷预测精度，降低电力系统规划决策的保守性，本文提出了一种基于小波-原子稀疏分解(WD-ASD)的超短期负荷预测模型。该模型使用模糊聚类算法提取相似日为历史数据，采用小波分解(WD)作为前置环节，以基于原子表达式的自预测和基于最小二乘支持向量机(LSSVM)的残余分量预测为基础构建原子稀疏分解(ASD)预测模型，分别对负荷的高低频分量进行预测，并将结果相加得到最终预测值。其中ASD分解过程由正弦原子库自适应匹配分解完成，并将粒子群算法(PSO)和正交匹配追踪(OMP)算法相结合以增强原子稀疏分解能力。实际负荷数据算例验证了所提方法的自适应性、快速性及有效性。

超短期负荷预测； 原子稀疏分解； 正交匹配追踪； 粒子群优化； 小波分解； 最小二乘支持向量机

1 引言

随着电力市场的开放，电力负荷预测成为了电能交易的重要环节，它为电力公司制定电价、发电计划、设备检修计划等提供了依据，其预测精度的高低将直接影响电力公司的经济效益。提高负荷预测精度，有利于减少系统备用及常规机组的出力，降低燃料成本。随着我国节能减排政策的逐步落实，提高负荷预测精度成为越来越重要的研究课题。尤其是其中的超短期负荷，由于在短期内波动大、随机性强、周期性低，因此对其进行预测的难度也更高。

近年来，各类负荷预测算法不断涌现，从建模原理上划分主要分为统计方法、学习方法和组合预测方法。统计方法只需根据负荷的历史数据，利用时间序列法、自回归模型等统计学方法得到预测值，该方法应用广泛，计算速度快，但对数据序列的平稳性要求较高[1,2]。学习方法主要运用近些年来较为热门的智能算法，如神经网络、支持向量机、极限学习机、混沌算法和数据挖掘等的自学习能力，根据大量数据样本建立起输入与输出之间的映射关系，再依据历史数据得到预测值，这种方法可根据不同地域及不同类型的负荷状况作出相应调整，预测精度较为理想[3-6]。组合预测方法是将多种预测方式进行组合后得到预测值，但预测精度依赖于组合方式中权重的选取[7]。

近年来，S. Mallat及Z. Zhang提出的原子稀疏分解法(Atomic Sparse Decomposition，ASD)成为研究热点[8]，它可在高度冗余的原子库中选择与原始信号高度匹配的分量，并且其原子库形式多样，因此被广泛应用于信号处理[9,10]领域，也有部分学者将其应用于各类预测模型的构建中。文献[11]将原子稀疏分解法与BP神经网络相结合，并将其应用于风电功率爬坡事件的预测，算例仿真验证了该方法的可行性，且预测精度较高，但由于该方法使用双字典集的分解算法，计算量较大。

鉴于原子稀疏分解法可依据实际数据趋势建立相应原子库，实现自适应匹配，在预测领域具有可行性，并考虑负荷数据本身具有的波动性及周期性，本文在文献[11]的基础上，提出基于小波分解(Wavelet Decomposition，WD)与原子稀疏分解法相结合的WD-ASD预测模型。该模型首先利用模糊聚类方法提取相似日，将WD作为前置环节，分解出多个相似日负荷数据中的低频周期分量以及高频波动分量，再使用ASD将其分解，对原子分量进行自预测，残余分量进行最小二乘支持向量机(Least Squares Support Vector Machine，LSSVM)预测，并将结果叠加后得到最终预测值。同时，本文针对ASD使用匹配追踪(Matching Pursuits，MP)算法分解速度慢的缺点，提出基于粒子群算法(Particle Swarm Optimization，PSO)与正交匹配追踪(Orthogonal Matching Pursuits，OMP)算法相结合的PSO-OMP优化的原子分解法，从而降低迭代次数，提高收敛速度。算例仿真和误差分析表明，本文所提方法具有较强的非平稳特性处理能力，且预测精度较高。

2 原子稀疏分解法

2.1 正弦原子库

原子稀疏分解算法可根据信号本身属性构建相应高度冗余的原子库，待分解的原子通过与原子库进行适应度匹配，从而分解得到具有具体表达式的最佳匹配原子，这组最佳匹配原子即可用来表示该信号。

对负荷数据进行分析，需要建立合适的原子库模型。负荷大小由该地区居民、工业等用电习惯决定，在一天中会定时出现早晚高峰，并伴随周期性，因此根据这一负荷特性，选择具有周期延续性及波动性的正弦原子，正弦原子实数形式如下：

gγ(t)=kγsin(ωt+φ)

(1)

式中，γ=(ω,φ)，为参数组，其中ω为原子的频率，φ为原子的相位；kγ为使‖gγ(t)‖=1的系数。正弦原子库是正弦原子经过平移、伸缩、调制而成。

2.2 正交匹配追踪算法

本文在S. Mallat等人提出MP算法的基础上，对分解每一步所选择的原子与已选择的所有原子进行正交化处理，保证在精度相同的前提下，收敛速度更快，该方法称之为正交匹配追踪算法(OMP)[12]。算法流程如下。

(2)

并令

s0=gγ(0)，u0=s0/‖s0‖

(3)

(2)匹配迭代第m次，将搜索到的最佳匹配原子gγ(m-1)与已选择出的所有原子做施密特正交化处理：

(4)

并对sm-1做归一化处理：

um-1=sm-1/‖sm-1‖

(5)

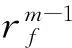
(6)

(4)根据迭代次数设定匹配停止准则，在进行n次迭代分解后，信号f可表示为：

(7)

2.3 基于PSO优化的OMP算法

由于穷举迭代的OMP算法计算量仍然较大，为此本文采用粒子群优化算法对OMP进行优化。PSO算法通过模拟鸟群觅食的运动行为来优化求解过程，算法简洁，具有较强的寻优能力[13]。

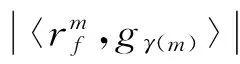
本文设置PSO算法的惯性权重w=0.7298，加速系数c1=c2=1.4962。PSO-OMP算法由于使用了正交化处理，会比MP算法具有更快的收敛速度，在保证信号重构精度的情况下，需要的迭代次数更少；另外，PSO优化算法能够更快搜索到最佳匹配原子，从而提高了算法整体运算速度。

3 WD-ASD预测模型

3.1 WD-ASD预测框架

本文以某地区2014年7月份一周负荷数据为例，通过对负荷历史数据进行特性分析，得到一周负荷数据，如图2所示，其中时间分辨率为15min。

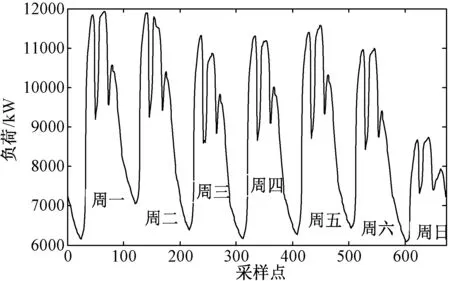
图2 一周负荷数据Fig.2 Load data in a week

由于负荷受日期、天气及社会影响较大，工作日与休息日的负荷差距较大，需对影响因素做量化处理。因此，本文使用模糊聚类算法找出多个历史相似日作为历史数据再进行预测，保证数据的周期性能够得到延续。由于提取的相似日具有明显周期性，因此可使用WD作为前置环节，对负荷数据进行分解。经WD五层分解后可得到低频周期性分量、非周期性分量及其他高频随机性分量，如图3所示。

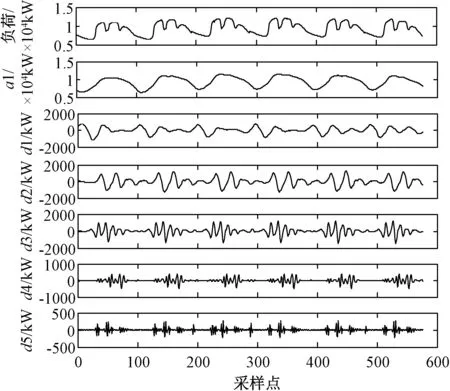
图3 小波分解图Fig.3 Wavelet decomposition diagram

由于这些具有非平稳特性和周期性的分量可由若干正弦分量构成，因此使用本文提出的具有正弦原子库的ASD模型分解预测，能够获得较为理想的预测精度。本文提出的WD-ASD组合预测算法预测过程如下。

(1)使用模糊聚类算法对星期类型、日最高气温、最低气温、平均气温及降雨量量化，提取出与预测日相似日期的负荷数据构成相似日负荷粗集[14]，量化表见表1。

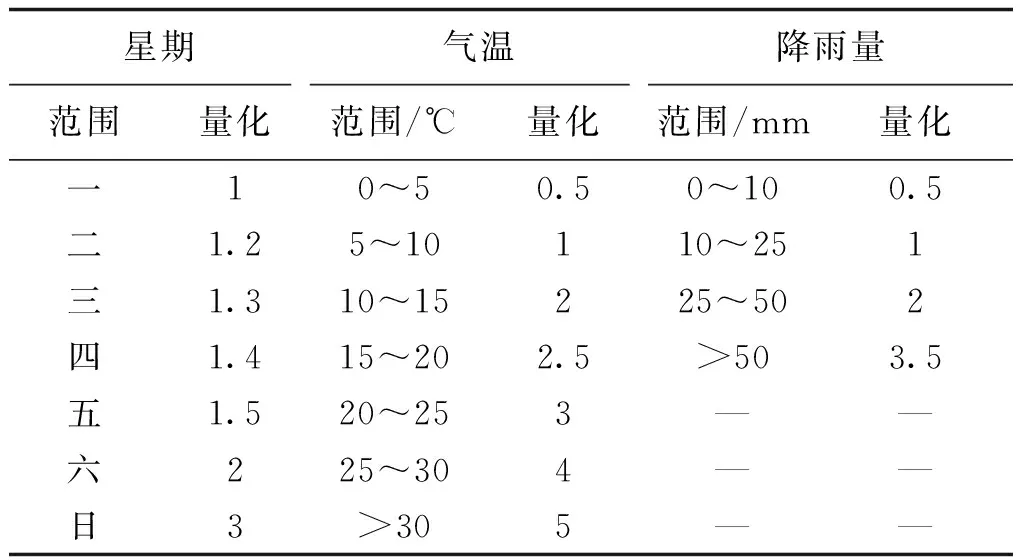
表1 模糊聚类量化表Tab.1 Fuzzy clustering quantization table

(2)将相似日的负荷数据粗集作为历史数据，即[P1(t1+m～t24),...,Pi(t1～t24),Pn+1(tj)],j∈[1,m]，其中P为每天24h的负荷数据，使用小波分解作为前置环节对相似日历史数据进行分解。综合考虑与ASD方法结合的预测精度，选择使用db4小波基对负荷数据进行5层小波分解。

(3)考虑各分量所具有的周期性，选择正弦原子库分别对高低频分量使用ASD预测模型进行预测。

(4)为了实现在线预测，采用多步长的滚动预测方式，在预测历史数据样本中，不断引入新预测数据，同时去除据预测值最远的旧数据，实时更新历史数据及预测值。

图4为使用WD-ASD模型预测第n+1天24h负荷的流程图。其中m代表时刻，初始值为1。

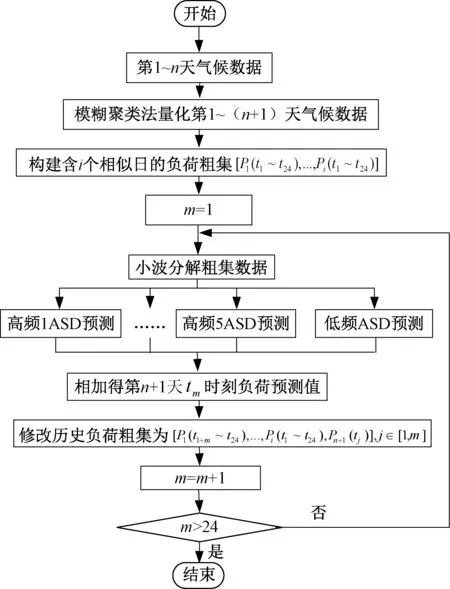
图4 预测模型流程图Fig.4 Prediction model flow chart

3.2 ASD预测模型框架

为综合考虑负荷同时具备的周期性及非平稳特性，本文构建正弦原子库，对WD得到的高频和低频分量均进行分解，有具体表达式的原子分量直接自预测，无具体表达式的残余分量输入最小二乘支持向量机中预测，可达到自适应分解预测负荷周期分量及随机分量的效果。在使用ASD时，需设置合理的迭代停止条件，使残余分量尽可能小，从而避免非平稳特性对LSSVM预测结果的影响。以低频信号为例，预测过程如下。

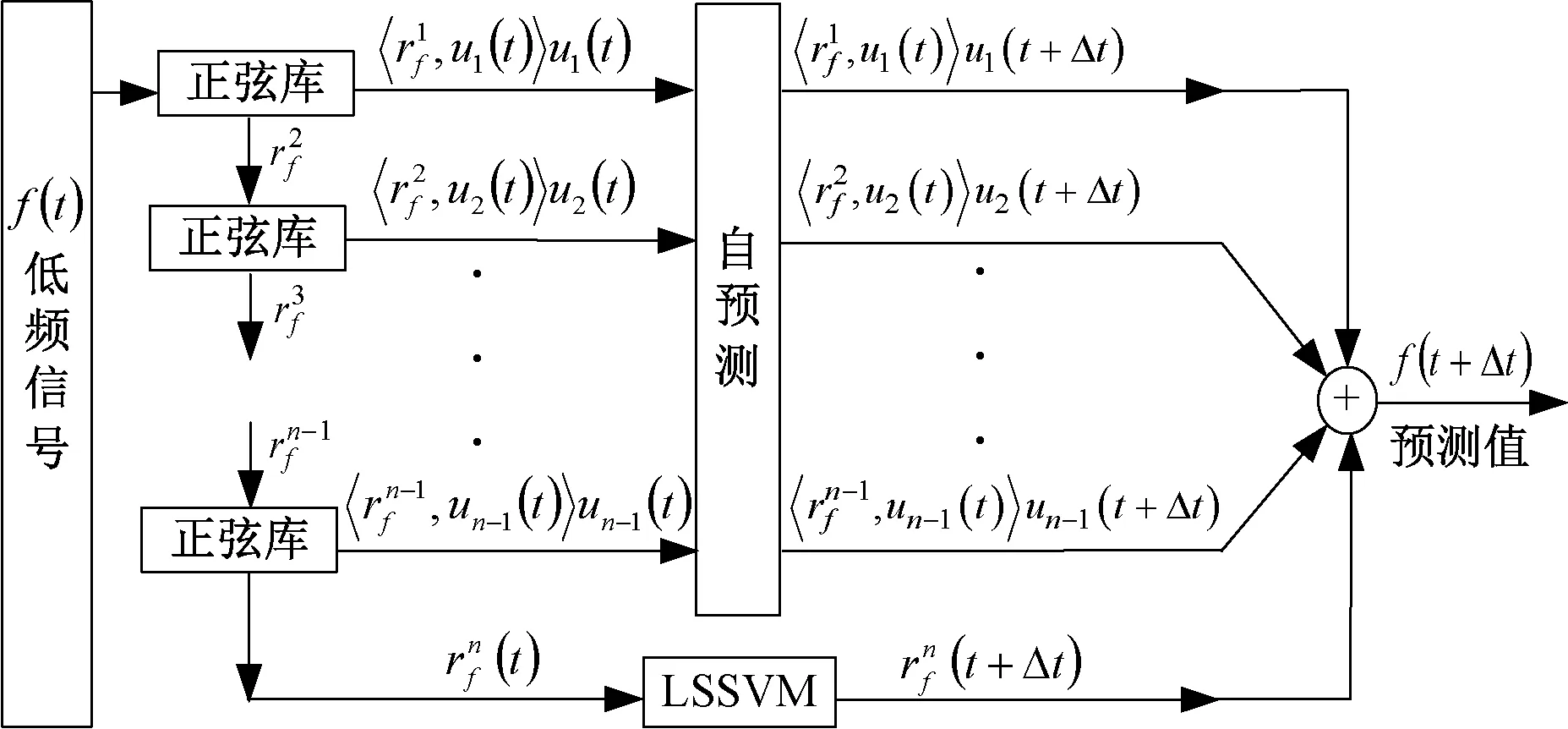
图5 ASD预测模型结构Fig.5 ASD forecasting model

(2)经原子稀疏分解后，对n-1个具有具体表达式的原子分量进行自预测，并将无表达式的残余分量作为LSSVM输入样本进行预测。

(3)自预测与残余分量预测结果的叠加值为低频信号预测值。以低频信号的分解预测为例，ASD预测模型结构如图5所示，其中Δt表示预测时间尺度。

4 实例分析

选取国内南方某地区2014年某时段实测负荷数据，进行算例验证。该地区最大负荷为13000kW，时间分辨率为15min，首先使用模糊聚类选取与预测日相似的相似日作为历史数据，再使用本文提出的WD-ASD预测模型逐步滑动预测未来时刻的负荷。其中历史数据经db4小波五层分解后，得到的低高频分量具有较明显变化规律，故可使原子稀疏分解法在分解次数较少时即可保证较高的预测精度，从而达到降低计算量、提高预测实时性的效果。经多次实验测试，本文算例中ASD分解5次即可取得较好结果。

4.1 不同预测尺度比较

超短期负荷预测指预测未来15min～4h的负荷数据，为验证本文所提短期负荷预测算法的有效性，对某地区7月18日做不同预测尺度的负荷预测。首先根据模糊聚类量化准则，对某地区7月1～18日的气候数据做相似度分析，相似度值如表2所示。提取相似度值大于0.99的4个相似日，将其对应的4天负荷作为历史数据。再使用WD-ASD预测模型对7月18日做负荷预测，预测结果及预测误差分别如图6和图7所示。预测尺度分别为15min、1h及4h，由于负荷数据采样时间分辨率为15min，因此预测尺度为15min时每次只预测1个采样点，预测尺度为1h时每次预测4个采样点，预测尺度为4h时每次预测16个采样点。

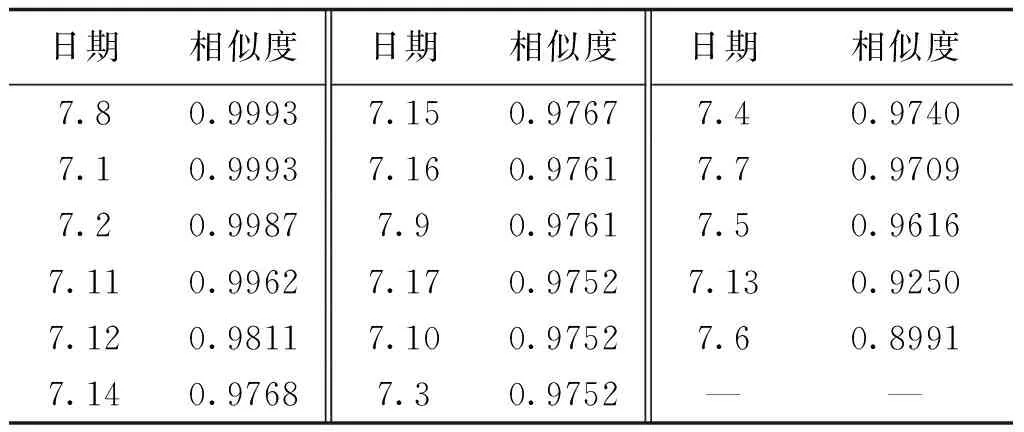
表2 预测日与历史日相似度值Tab.2 Similarity values of predict and historical day

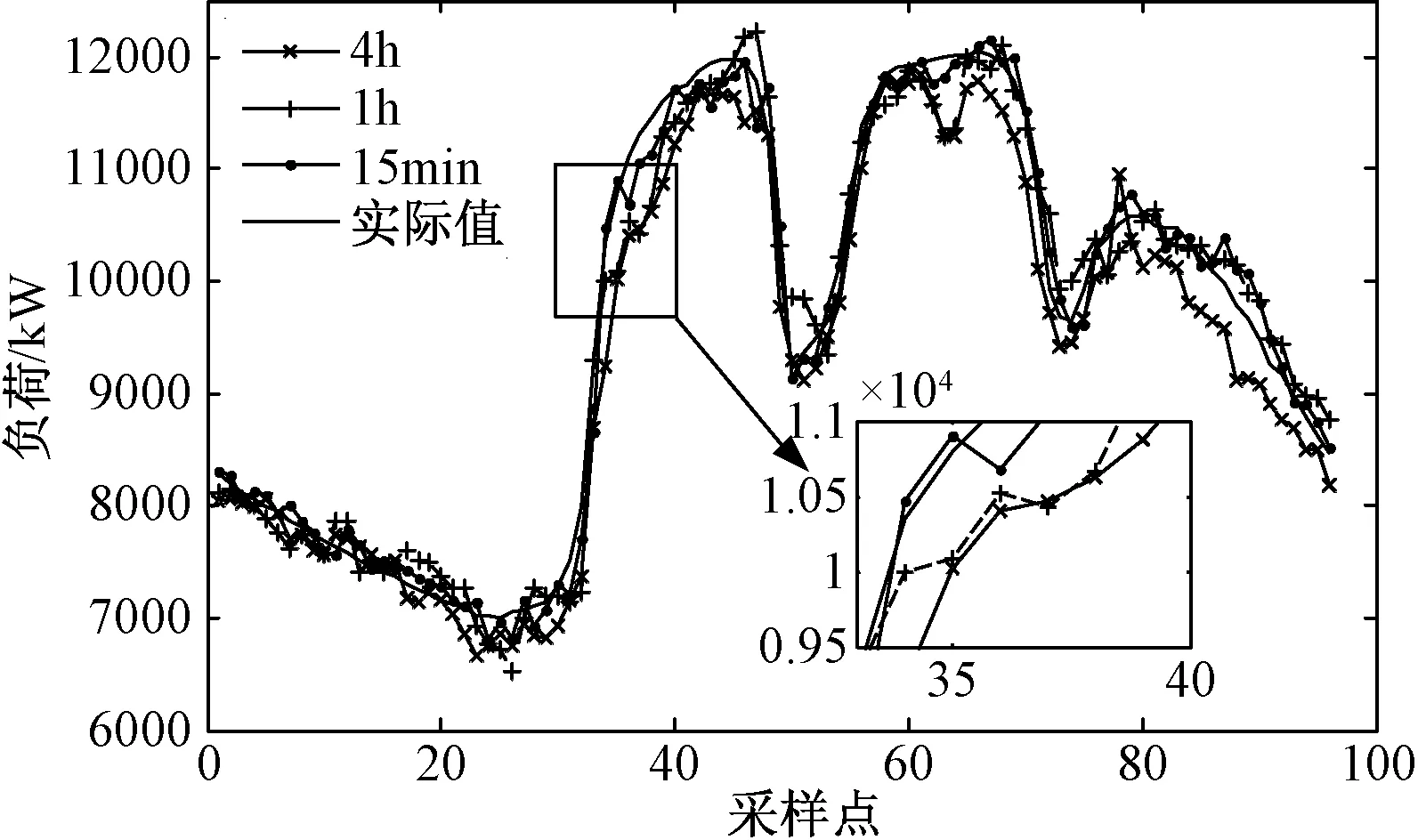
图6 7月18日预测结果Fig.6 Predict results of 18 July

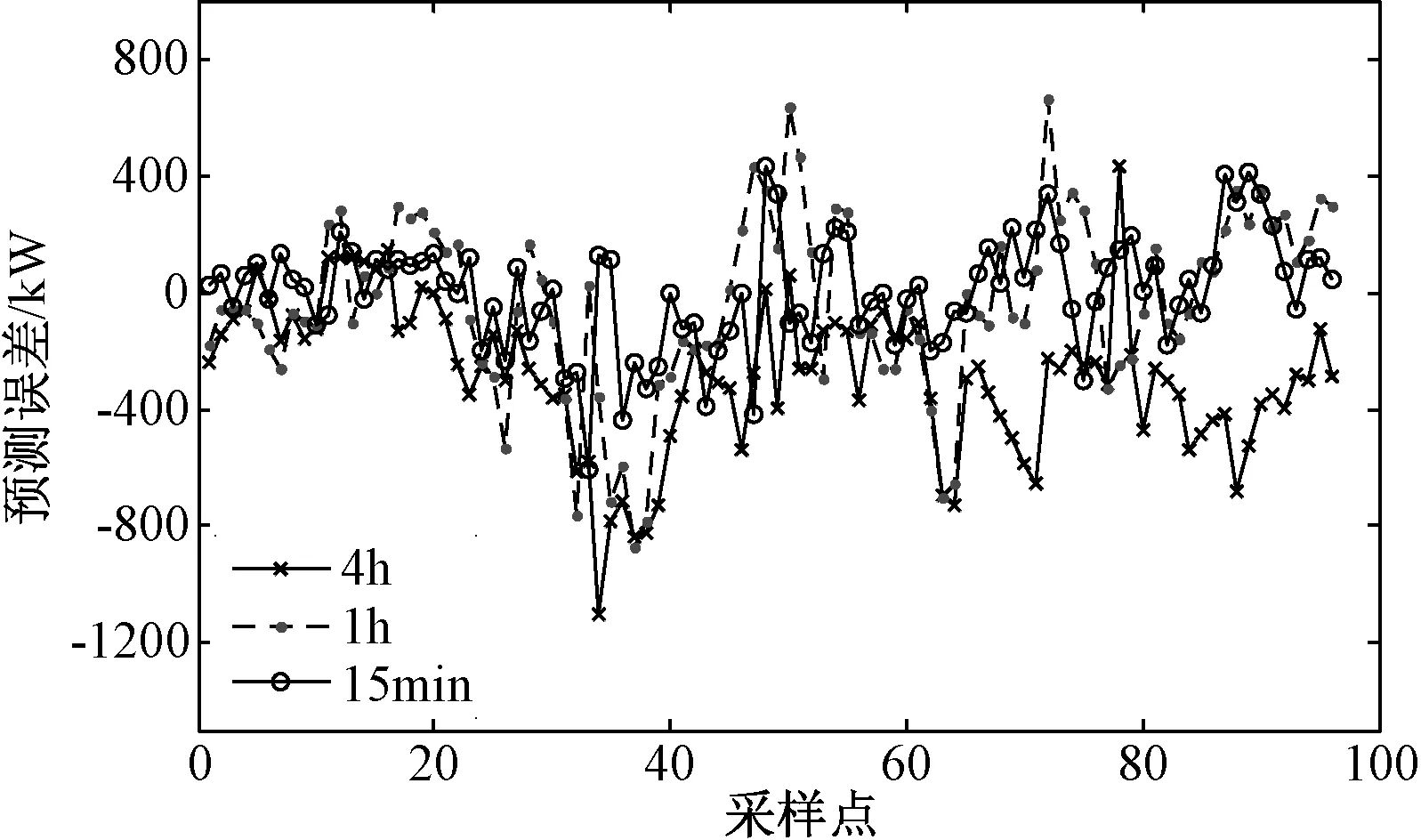
图7 预测误差曲线Fig.7 Prediction error curve

为了更直观地对比，可对预测结果进行定量分析，由于预测误差大小与日最大负荷直接相关，因此采用国际上普遍的归一化绝对平均误差eNMAE和归一化均方根误差eNRMSE为依据，结果如表3所示。两误差的表达式为：

(8)

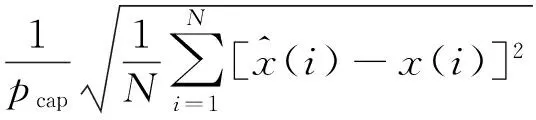
(9)

表3 预测结果误差对比Tab.3 Error comparison of predict results

由图6、图7及表3综合分析可知，预测误差会随着预测尺度的增长而增大，当预测尺度越小，预测精度越高，说明本文所提算法能够对负荷进行超短期高精度预测。

4.2 不同预测算法比较

为进一步验证本文提出的WD-ASD预测模型的有效性，选取该地区6月份负荷使用模糊聚类算法提取相似日作为历史数据，预测7月1日的96个负荷采样点，并与只使用LSSVM的预测方法及使用WD与LSSVM结合(WD-LS)的预测方法比较。预测结果及预测误差分别如图8和图9所示，其中对第15和16个采样点局部放大，对整体96个数据做误差分析结果，如表4所示。

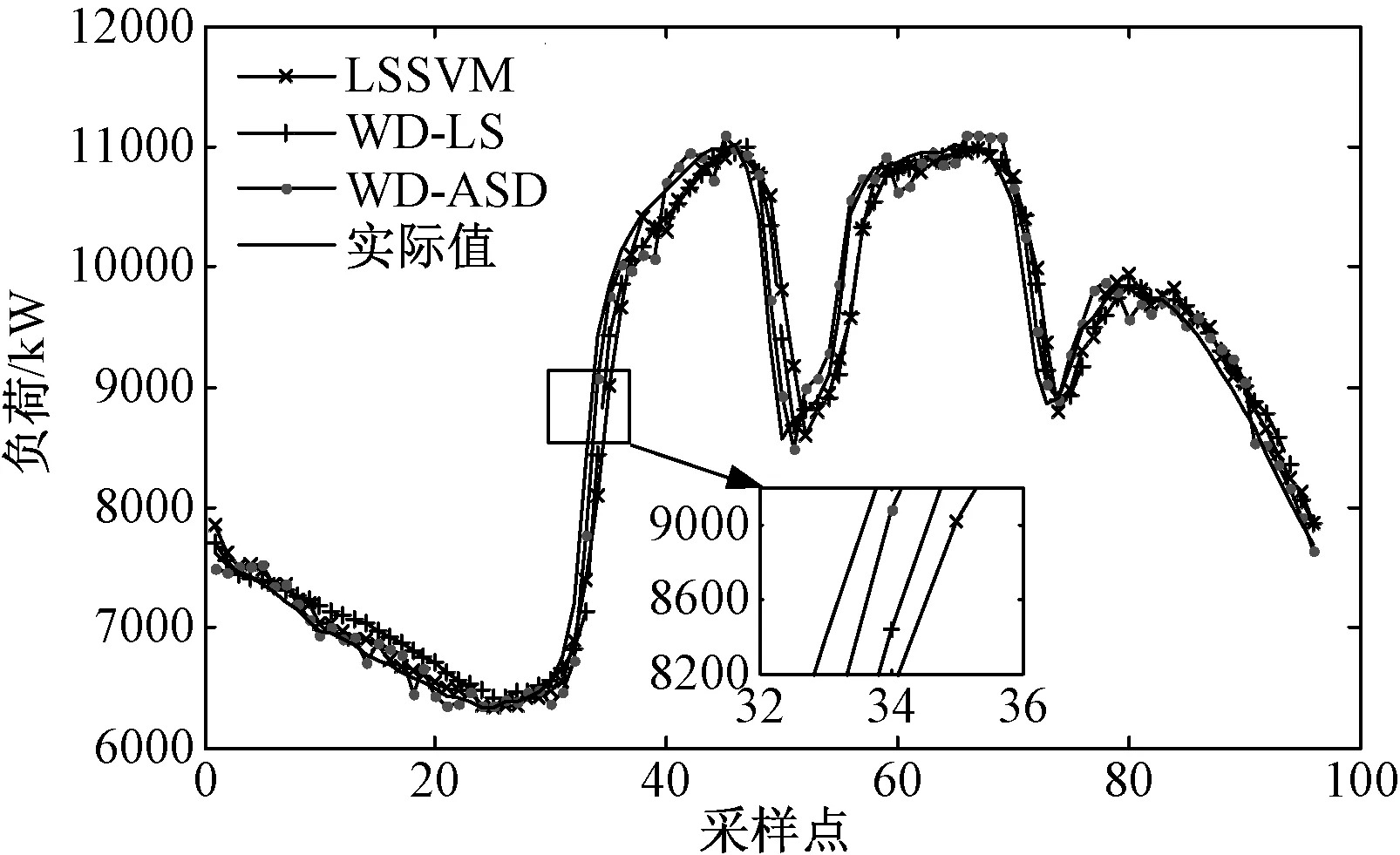
图8 预测结果对比图Fig.8 Comparison of predict results

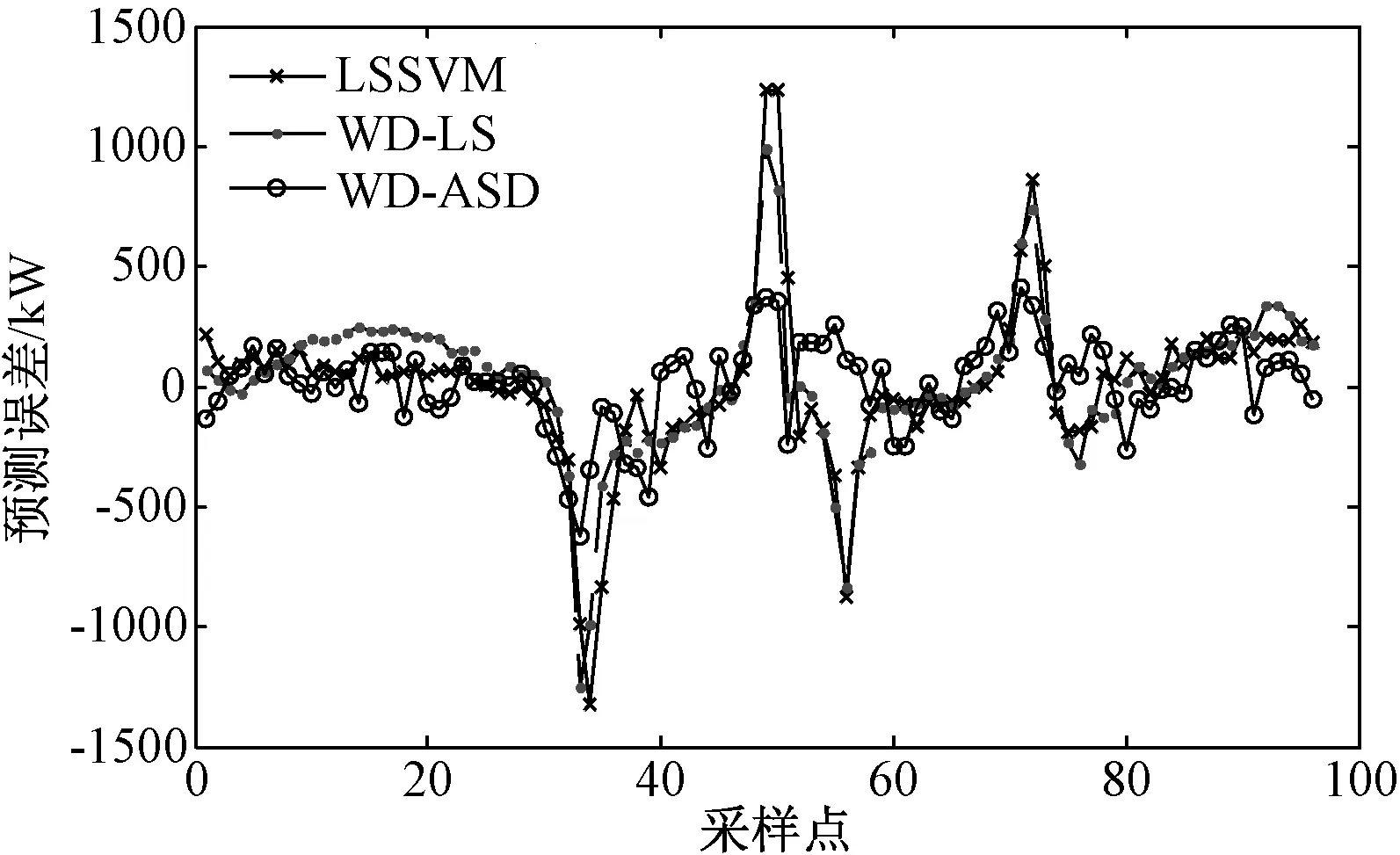
图9 预测误差对比图Fig.9 Comparison of prediction error

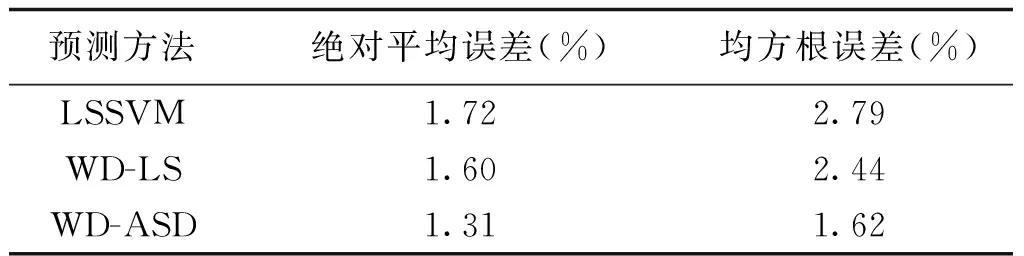
预测方法绝对平均误差(%)均方根误差(%)LSSVM1.722.79WD-LS1.602.44WD-ASD1.311.62

由图8可知，在负荷大幅度上升及下降区域，LSSVM和WD-LS的预测结果具有明显的滞后性，而本文所提WD-ASD预测模型滞后效应不明显。同时从图9的预测误差曲线中可看出，WD-ASD预测误差稳定在[-500，500]之内，而LSSVM及WD-LS预测结果波动较大。由表4可知，WD-ASD预测模型的误差最小，说明其预测精度较高。

5 结论

针对负荷数据所具有的周期性及波动性，本文提出了基于WD-ASD的超短期负荷预测模型。首先在较多历史数据中挑选出与预测日的气象及日期因素较为类似的相似日作为历史数据，缩小数据量；再将小波分解与原子稀疏分解相结合形成WD-ASD预测模型，其中利用PSO-OMP算法对原子稀疏分解过程进行优化。本文使用该方法对实际算例进行仿真分析，并与常规预测方法作对比，得出的主要结论如下。

(1)本文构建的WD-ASD预测模型在提前15min、1h及4h的预测结果精度较高，因此可进行超短期负荷预测。

(2)WD-ASD预测算法中依据负荷数据特性构建了正弦原子库，可适应不同时间段内的气象环境变化，自适应预测，有效处理负荷数据中的波动性及周期性。

(3)WD-ASD算法相比于常规预测方法，在负荷发生大幅度波动时，能够实现较好的预测，误差小，可降低电力系统部门宏观调度时的保守性。

本文提出的WD-ASD算法可为电力部门提供较为可靠的预测结果，但预测时易受历史相似数据的影响，若相似日选取不当，则预测结果会产生较大误差。因此，下一步对负荷进行超短期预测研究时，可重点研究聚类算法，挑选更为精确的相似日集合作为历史数据，使预测精度更高。

[1] Fan S，Hyndman R J．Short-term load forecasting based on a semi-parametric additive model[J]．IEEE Transactions on Power Electronics，2012，27(1)：134-141.

[2] 孙欣尧， 王雪，吴江伟，等(Sun Xinyao，Wang Xue，Wu Jiangwei，et al.)．分布式协同网络用电负荷分层加权概率预测方法(Feature weighting based on hierarchical probabilistic load forecasting in distributed collaborative network)[J]．仪器仪表学报(Chinese Journal of Scientific Instrument)，2014，35(2)：241-246.

[3] 张淑清， 任爽，师荣艳，等(Zhang Shuqing，Ren Shuang，Shi Rongyan，et al.)．基于多变量气象因子的LMBP电力日负荷预测(Multiple weather factors-based LMBP method for daily power load forecasting)[J]．仪器仪表学报(Chinese Journal of Scientific Instrument)，2015，36(7)：1646-1652.

[4] 张淑清， 师荣艳，张立国，等(Zhang Shuqing，Shi Rongyan，Zhang Liguo，et al.)．混沌预测模型改进及在电力日负荷预测中的应用(Improvement of chaotic forecasting model and its application in power daily load forecasting)[J]．仪器仪表学报(Chinese Journal of Scientific Instrument)，2016，37(1)：208-214.

[5] Lee Woo-Joo，Hong Jinkyu． A hybrid dynamic and fuzzy time series model for mid-term power load forecasting[J]． Electrical Power and Energy Systems，2015，64：1057-1062.

[6] 赵立权， 谢妮娜(Zhao Liquan，Xie Nina)． 基于小波变换和改进RVM的电能质量扰动分类(Classification of power quality disturbances based on wavelet transform and improved RVM)[J]． 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2013，32(4)：74-78.

[7] 尹星露， 肖先勇， 孙晓璐(Yin Xinglu，Xiao Xianyong， Sun Xiaolu)．基于预测有效度和马尔科夫-云模型的母线负荷预测模型筛选与变权重组合预测(Bus load forecasting model selection and variable weights combination forecasting based on forecasting effectiveness and Markov chain-cloud model)[J]． 电力自动化设备(Electric Power Automation Equipment)， 2015，35(3)：114-119.

[8] Mallat S，Zhang Z．Matching pursuits with time-frequency dictionaries[J]． IEEE Transactions on Signal Processing， 1993， 41(12)：3397-3415.

[9] 王宁， 李林川， 贾清泉，等(Wang Ning，Li Linchuan，Jia Qingquan，et al.)． 应用原子分解的电能质量扰动信号分类方法(Classification of power quality disturbance signals using atomic decomposition method)[J]．中国电机工程学报(Proceedings of the CSEE)，2011，31(4)：51-58.

[10] 陈雷， 郑德忠， 赵兴涛， 等(Chen Lei，Zheng Dezhong，Zhao Xingtao，et al.)． 基于FFT和优化匹配追踪的谐波/间谐波检测(Harmonic and inter-harmonic detection based on FFT and optimized matching pursuit)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016，35(2)：7-12.

[11] 崔明建， 孙元章， 柯德平(Cui Mingjian， Sun Yuanzhang， Ke Deping)．基于原子稀疏分解和BP神经网络的风电功率爬坡事件预测(Wind power ramp events forecasting based on atomic sparse decomposition and BP neural networks)[J]．电力系统自动化(Automation of Electric Power Systems)，2014，38(12)：6-11.

[12] 侯世英， 张文玉， 孙韬， 等(Hou Shiying， Zhang Wenyu， Sun Tao， et al)．基于正交优化时频原子分解算法的电能质量扰动匹配特征分析(Analysis on matching features of power quality disturbances based on orthogonal optimization of time-frequency atom decomposition)[J]．电网技术(Power System Technology)， 2013, 37(3)：647-652.

[13] 王冰山， 周步祥， 肖贤， 等( Wang Bingshan， Zhou Buxiang，Xiao Xian，et al.)．基于量子行为粒子群算法-混沌神经网络的电力系统负荷预测(Power system load forecasting based on quantum behavior particle swarm optimization algorithm-chaotic neural network)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2014，33(6)：7-12.

[14] 张平， 潘学萍， 薛文超(Zhang Ping，Pan Xueping， Xue Wenchao)．基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测(Short-term load forecasting based on wavelet decomposition，fuzzy gray correlation clustering and BP neural network)[J]．电力自动化设备(Electric Power Automation Equipment)，2012，32(11)：121-125.

Short-termloadforecastingbasedonWD-ASDoptimizedbyPSO-OMP

QU Zheng-wei1, ZHANG Kun1, WANG Yun-jing1, HAN Yan-feng1, HAO Li-li2, WANG Chong-yi3

(1. Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province, Yanshan University, Qinhuangdao 066004, China; 2. School of Electrical & Electronic Engineering, North China Electric Power University, Baoding 071003, China; 3. Beijing E Town International Development & Construction Co. Ltd., Beijing 100176, China)

In order to improve the accuracy of load forecasting and reduce the conservatism in power system planning decisions, this paper proposes a short-term load forecasting model based on the combination of wavelet decomposition and atomic sparse decomposition(WD-ASD). This model uses fuzzy clustering algorithm to extract the data of a similar day as the historical data. Wavelet decomposition (WD) is used as the prepositive step. Atomic sparse decomposition prediction model is set up to predict the high frequency and low frequency components of load based on the adaptive prediction which uses atomic expression and the residual component prediction which uses least squares support vector machine (LSSVM). Then the two results are added to get the final predictor. The ASD process is obtained by adaptive matching decomposition from the sine atomic library. In addition, particle swarm optimization (PSO) and orthogonal matching pursuit (OMP) algorithm are combined as PSO-OMP to optimize the atomic sparse decomposition. This method enhances the decomposition ability. The actual load example shows the adaptivity, rapidity and validity of this method.

short-term load forecasting; atomic sparse decomposition; orthogonal matching pursuit; particle swarm optimization; wavelet decomposition; least squares support vector machine

2016-08-08

河北省高等学校科学技术研究项目(QN2016064)

曲正伟(1979-)， 男， 吉林籍， 副教授， 博士， 主要研究方向为现代电磁测量技术及仪器；张 坤(1992-)， 女， 宁夏籍， 硕士研究生， 主要研究方向为电能质量与负荷预测。

10.12067/ATEEE1608014

1003-3076(2017)12-0039-07

TM714