协调运行经济性与安全性的电力系统连锁故障风险控制方法

杨超平， 姚 锐， 张 爽， 顾雨嘉， 沈 沉

(1. 国网宁夏电力公司电力科学研究院， 宁夏 银川 750001)(2. 电力系统及发电设备控制和仿真国家重点实验室， 清华大学电机系， 北京 100084)

协调运行经济性与安全性的电力系统连锁故障风险控制方法

杨超平1， 姚 锐2， 张 爽1， 顾雨嘉1， 沈 沉2

(1. 国网宁夏电力公司电力科学研究院， 宁夏 银川 750001)(2. 电力系统及发电设备控制和仿真国家重点实验室， 清华大学电机系， 北京 100084)

连锁故障对电力系统的危害巨大，因此有必要在连锁故障模拟和风险评估的基础上，实现对连锁故障风险的有效控制。本文提出了一种基于连锁故障模拟和风险评估结果的风险控制方法。首先通过对风险展开式进行近似线性化，求得连锁故障风险的梯度；然后利用风险梯度建立了协调控制优化模型，通过求解得到全系统发电出力调整和切负荷策略，在有效降低风险的前提下最小化控制成本，实现运行经济性与安全性的协调。为了克服线性化带来的较大误差，进一步提出了风险协调控制优化多步迭代方法。4节点测试系统和宁夏电网算例结果验证了所提方法的正确性和计算效率。本文所提方法能够用于离线预想故障分析，并具有在线分析和辅助决策的潜力。

连锁故障； 风险； 经济性； 安全性； 协调控制

1 引言

电力系统连锁故障[1-3]是由一个或者多个初始故障引发的元件相继退出的过程，连锁故障使系统变得脆弱，并可能造成大范围停电事故，带来严重的社会经济损失[4]。因此，人们一直致力于研究连锁故障的机理与特征[5-7]，并希望对连锁故障进行预警和控制，以降低连锁故障风险。

很多连锁故障是由于元件相继过载退出运行而引起的，因此降低系统元件的负载率可以有效预防连锁故障[7,8]。但是，即使当前系统没有过载，一些元件仍然可能处于满载状态，或者系统刚好满足N-1准则；当系统发生随机故障、隐故障或者运行状态发生偏移后，产生过载和连锁故障可能性依然很高。因此，连锁故障和大停电的预防控制应当结合连锁故障风险评估结果，有针对性地考虑可能的连锁故障路径及其风险。一些研究基于风险评估的概念给出了考虑不确定性的安全控制优化方法。这些方法或者考虑当前断面下的风险，用严重度指标量化风险，并将风险作为约束或作为加权放入目标函数中[9]，或者采用详细建模系统动态和在一级故障下系统状态的变化并进行风险评估[10]。然而上述方法没有考虑后续多级连锁故障的影响，因此会遗漏一些高风险故障发展模式，从而使连锁故障风险评估结果不够准确。另外，严重度指标[11]或者类似指标没有明确的物理意义，其在优化控制模型中的取值方法也缺乏明确的依据，从而影响了其实用性。

本文考虑大规模电网多级连锁故障的风险，建立了综合考虑当前控制代价与系统运行风险的优化控制方法。借助连锁故障模型，对电网中连锁故障进行模拟[12]；利用连锁故障模拟结果建立了系统状态与连锁故障风险的关系，求取了后续风险的近似梯度。利用该风险梯度，建立了协调控制优化模型。本文方法基于直流潮流模型，通过求解模型，得到全系统发电机出力调整和切负荷策略。该协调控制优化模型能够在有效降低连锁故障风险的条件下最小化运行成本，从而实现运行成本与系统风险的协调控制。利用本模型，进一步实现了多步迭代的协调控制方法，克服了线性化方法在距离初始运行点较远时误差较大的问题。与传统方法相比，本文方法基于物理意义明确的风险指标，便于实际电力系统分析使用。

2 风险协调控制的基本思路

连锁故障发展过程中，随着潮流转移可能会出现越限的情况，调度员会调整系统状态以降低风险。但调度员每次做出的调整并不能完全消除风险，此后仍可能发生后续连锁故障，且后续故障的发生具有一定随机性。系统连锁故障的可能发展路径可以建模为树状结构[7]，如图1所示。

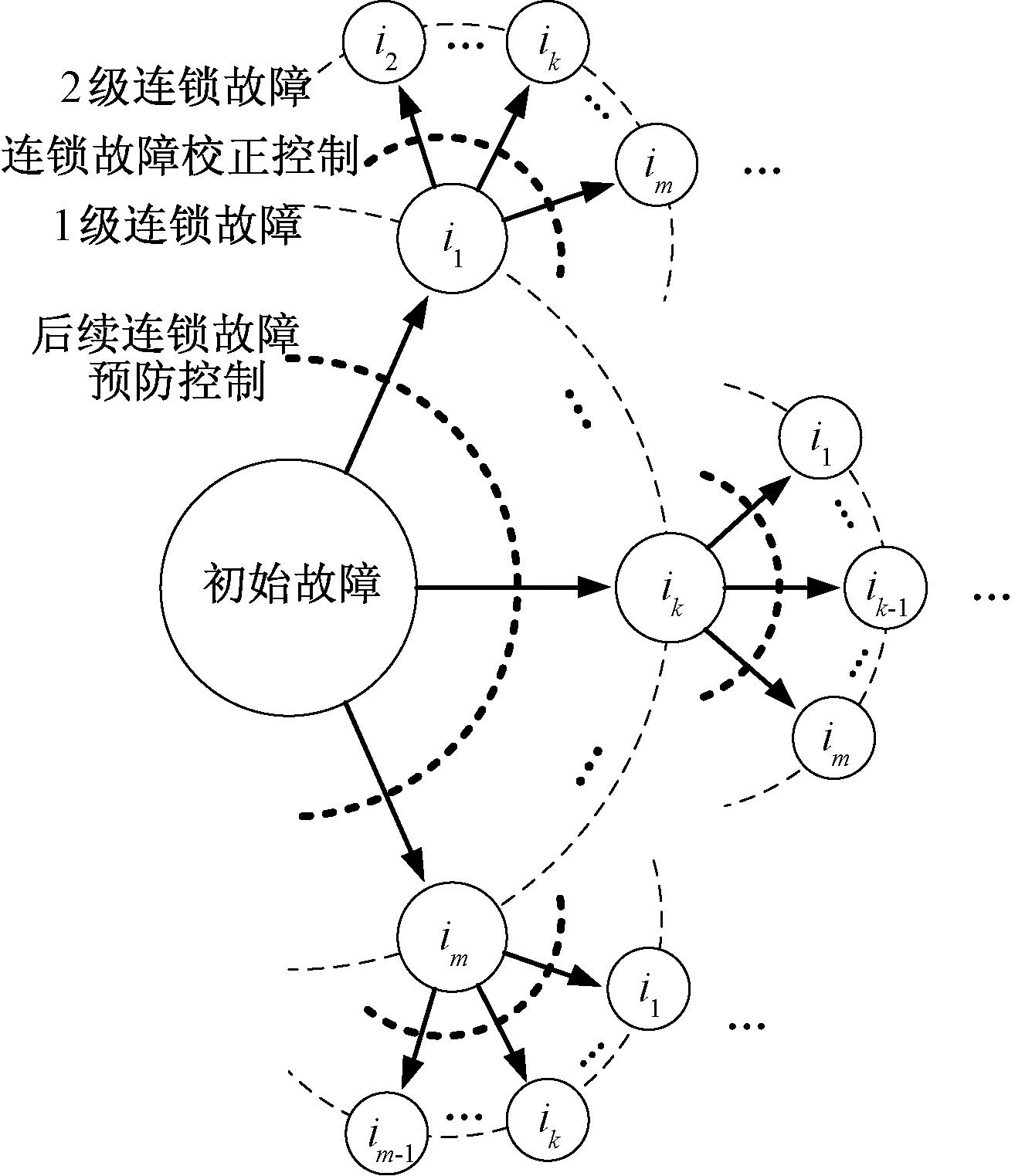
图1 连锁故障发展树状结构图Fig.1 Tree structure of cascading outage paths

按照本文所假设的背景，从初始故障发生后研究连锁故障发生的可能路径，即初始故障为树的根节点，称为0级节点，后续各级故障分别为1级、2级……节点，节点可用开断的元件编号表示，那么每一个连锁故障发展路径都可以用元件开断序列表示，如(ik1ik2…ikn)。每级故障后调度员会调整系统状态，以C(ik1ik2…ikn)表示故障序列(ik1ik2…ikn)发生后调度员操作的成本，可用负荷损失量或经济损失来度量。后级连锁故障的发生概率取决于之前的故障序列，因而第kn+1级故障的发生概率可用Pr(ikn+1|ik1ik2…ikn)表示。那么系统连锁故障风险R为：

(1)

式中，C0为初始故障发生后由于系统采取控制措施而产生的成本。式(1)的计算采用文献[7]中的连锁故障模型和风险评估方法，即采用基于准动态方法的多时间尺度连锁故障模型进行连锁故障模拟[6]，从而体现连锁故障的多时间尺度特性，并在连锁故障中加入时间因素。该模型与OPA(ORNL-PSERC-Alaska)模型等传统连锁故障模型相比，提高了建模的合理性和实用性。风险评估采用基于马尔科夫树搜索的方法[7]，通过优选并搜索高风险故障路径，能够实现连锁故障风险的高效评估，适应电力系统运行过程中风险评估的需求。

初始故障后的控制措施一般由调度员执行。本文采用直流潮流模型，故对应调度员控制的传统模型为直流最优潮流(DC-OPF)，而控制手段为调度中常用的调整发电机出力和调度员切负荷。因此C0可看作初始故障后调度控制的成本。令

(2)

式中，R′为初始故障后发生连锁故障的风险。由式(1)和式(2)得R=C0+R′，即期望损失(总风险)为初始故障后调度控制成本与后续连锁故障风险之和。

实际系统运行中，各类元件故障事件均有一定发生概率(不论其多么小)，因此式(2)中各级连锁故障的概率一般为正数。而当故障级数积累到一定程度后，总会有损失发生。因此R′总不为0，即后续连锁故障风险只能尽可能降低而无法完全消除。我们希望以尽量小的控制代价将连锁故障风险降低到可接受的程度，用数学语言表示为：

(3)

式中，x表示调度控制后的系统状态，初始故障后的调度控制成本C0受x的影响，而控制的目标为使成本C0(x)最小化；g(x)≤0表示系统状态应满足的约束，包括潮流方程约束、支路潮流约束、发电功率上下界约束等。同时，后续各级连锁故障均取决于调度控制后的状态x，即R′可看作是x的函数。风险协调控制需要首先将风险限制在目标范围内，即不高于某个预设值RE的水平。因此，式(3)所示的风险协调控制基本模型期待的作用即在有效控制风险的条件下，使调度控制成本最小。在模型中，控制成本C0(x)代表控制的经济性，而R′(x)代表系统运行的安全性。因此该协调控制模型体现了经济性与安全性的协调。而在式(3)中若去除连锁故障风险约束，则该模型退化为传统的调度控制模型。

3 风险协调控制模型

3.1 风险梯度的求取

下面考虑在某个初始故障发生后，如何进行协调控制，并获得调度后的系统状态x。如果能够将式(3)中的各项显式表示为控制变量和当前系统状态变量的函数，即可建立并求解协调控制模型。式(3)中的控制代价C0可以显式地表示为系统状态的函数，而后续连锁故障风险R′的形式比较复杂，难以用x显式表达，因此需要重点研究如何建立R′与系统状态x之间的关系。

由于连锁故障是一个复杂的过程，其中各级状态之间的影响关系复杂，量化后续连锁故障风险与状态的关系难度较大[13]。为了实现协调控制，一种方案是采用演化计算方法[14]，通过随机独立尝试优化策略和演化算法的优选机制，逐渐得到合适的策略。这种方法的优点是能够很好地应对连锁故障过程复杂性的特点，具有全局寻优能力，然而其显著的缺点是计算量非常大，且演化计算方法的性能并不稳定，在计算效果和效率方面均没有充分保证。而另一种方案是采用线性化的方法[15,16]，若将传统调度模型调整后的系统状态称为原工作点，则可以在工作点附近将风险进行线性化近似，从而得到控制变量对风险的灵敏度，进而构建风险协调控制模型。该方法的缺点是当距离原工作点较远时，或者系统风险表达式在数学上的结构出现变化(如由于初始状态或系统参数改变，导致对应调度优化模型最优点的基变量改变)时，线性化即会失效。然而由于该方案具有确定性的搜索策略，算法具有较好的数值稳定性，且计算效率较高，因此选取线性化方法构建风险协调控制模型。

若将第一级状态概率简记为Pr(1)，该级状态前的系统状态为x，假设每个可能的一级故障的发生概率为初始故障后系统状态x的函数Pr(x)(如OPA模型、隐故障模型等)，那么容易求得第一级各状态概率对x的偏导数∂Pr(1)/∂x。将式(3)中的第一级故障概率Pr(1)提取公因式，得到：

(4)

式中，C′(ik1)为所有后续连锁故障风险归算到一级故障的等效成本，即

(5)

求R′对x的偏导数，得到

(6)

式(6)为后续连锁故障风险在系统状态空间的梯度，而负梯度对应的方向为风险最速下降方向。如能求得该梯度值，则可用其降低连锁故障风险。在式(6)中对应各个一级故障的∂Pr(ik1)/∂x易求得，而∂C′(ik1)/∂x的计算需要对后续各级连锁故障概率以及损失均进行详细分析，计算非常复杂。因此为了减轻计算负担，本文暂不考虑x对C′的影响，即假设∂C′(ik1)/∂x=0，因而后续连锁故障风险梯度为：

(7)

式中，各C′(ik1)项可对图1所示的连锁故障事件树进行遍历模拟，并根据式(5)计算得到。

3.2 建立协调风险控制模型

在实际连锁故障分析与调度控制中，常用直流潮流模型描述并求解系统状态[17]。在直流潮流模型中，系统状态可用各节点的负荷功率Pd和发电功率Pg表示，即x=[PdT,PgT]T，本文中假设系统的调度操作为全系统发电机有功出力调整和切除负荷。假设用传统的调度控制模型得到的系统状态为x0=[Pd0T,Pg0T]T，相应的后续连锁故障风险为R′(x0)，则系统状态变为x=[PdT,PgT]T时，后续连锁故障风险近似为：

R′(x)≈R′(x0)+R′(x-x0)

(8)

相应地，各个一级故障概率近似为：

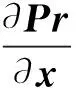
(9)

式中，Pr(x)为系统状态为x时各ik1故障概率Pr(ik1)组成的列向量。故障概率应在[0,1]区间内，因此需要对系统状态调整后一级故障的近似概率进行限幅，引入辅助变量Pr+和Pr-及如下约束：

(10)

式中，Pr+和Pr-为非负数。令MPr为足够大的数，即

0≤Pr+≤MPr,0≤Pr-≤MPr

(11)

注意到R′(x)=C′T(x)Pr(x)，其中C′(x)为系统状态为x时各C′(ik1)组成的列向量，并且有假设∂C′(ik1)/∂x=0，即近似认为C′(x)=C′(x0)，那么修正后的连锁故障风险R′(x)为：

由式(3)、式(10)～式(12)可得协调控制模型：

(13)

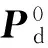
与传统的DC-OPF模型相比，模型式(13)加入了风险控制约束(即第3～5个约束表达式)，因此在相同系统状态和参数下，式(13)计算得到的最优值必然不小于DC-OPF。当ΔR′≤0时，风险约束不起作用，模型计算得到的结果将和DC-OPF相同。当ΔR′>0时，风险约束发挥作用，预期使风险降低，并使得模型得到的最优值大于DC-OPF，即降低风险将会以控制成本增加为代价。

4 基于多步迭代的协调控制

在求解协调风险控制模型式(13)时，需要首先确定合适的ΔR′。由于风险梯度是近似值，当ΔR′较大时可能出现较大误差，因此ΔR′的取值不宜过大。然而只有ΔR′取较大的值时，才能有效降低连锁故障风险。因此在ΔR′取值方面存在矛盾。

为了解决ΔR′的取值问题，考虑采用小ΔR′步长多步迭代的方法实现有效的连锁故障风险控制。在模型中模拟执行一次风险优化控制(其结果并不作为实际的控制策略)后，再进行连锁故障风险评估，并在新的运行点处进行线性化，求得新的风险梯度并在模型中模拟实施控制，如此往复进行多步风险控制迭代，就能够将风险控制的效果累积，从而有效地降低风险。该多步迭代的控制策略制定流程如图2所示。

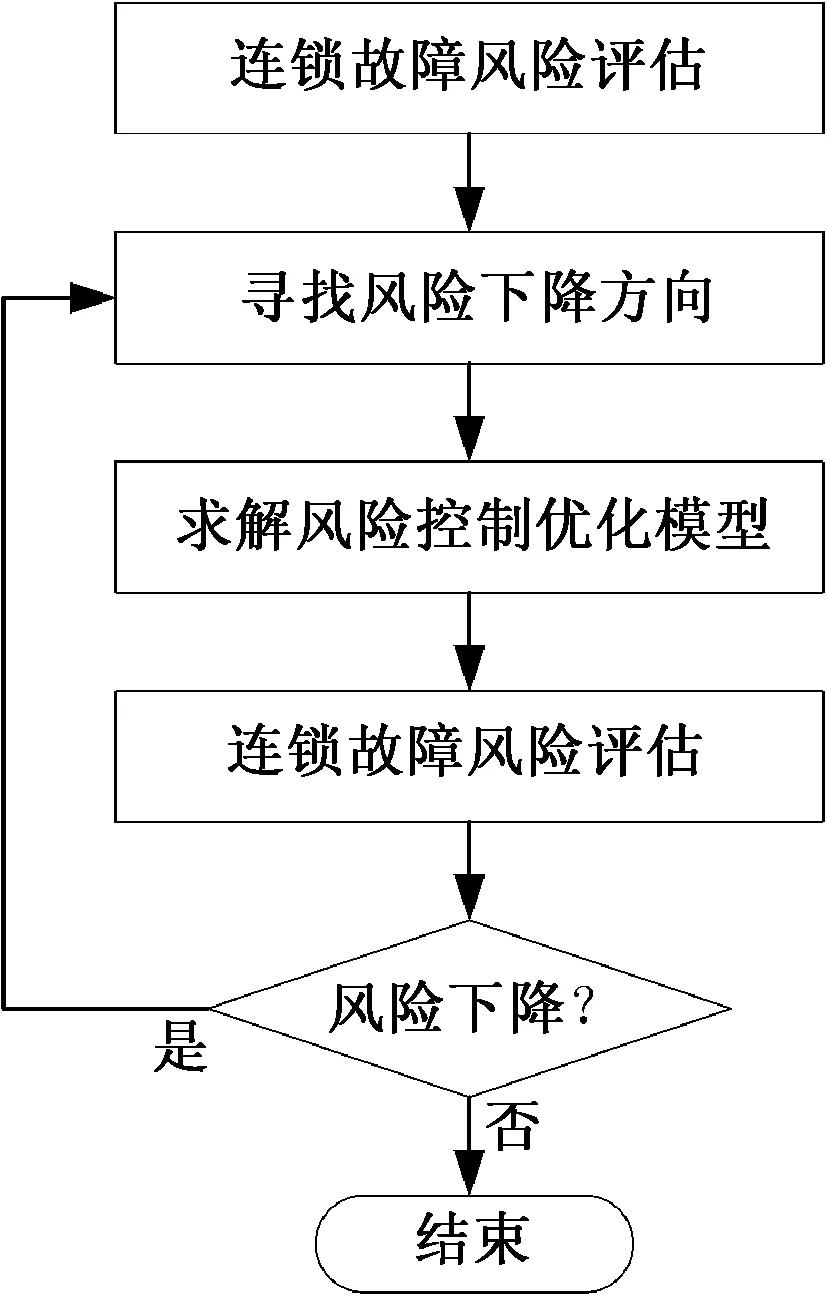
图2 连锁故障风险控制迭代流程Fig.2 Procedures of iterative coordinated risk mitigation

在每一步迭代中，首先利用上一步得到的风险评估结果求得连锁故障风险的梯度，并求解风险协调优化模型式(13)，将模拟执行控制策略后的系统模型进行连锁故障风险评估。如果评估得到的连锁故障风险比上一步降低，则说明控制有效，进行下一轮次迭代；否则结束流程。

利用多步迭代的方法，可以克服风险表达式线性化仅在原始工作点附近有效的缺点，从而使控制变量在较大范围内变动，实现对风险的有效控制。但其缺点是要进行多次风险评估，因此效率比单次求解风险协调控制模型的方法略低。

5 算例分析

5.1 测试4节点系统

(1)近似风险梯度计算验证

首先利用4节点系统验证风险梯度计算的准确性，系统包含2个负荷节点和2个发电节点，如图3所示。

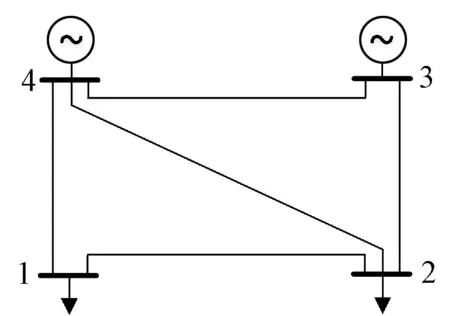
图3 测试4节点系统图Fig.3 Schematic of 4-bus test system

选取支路2-3开断为初始故障。控制成本为调度员控制切除的负荷量(标幺值)，风险为后续连锁故障中损失的负荷量(标幺值)。将系统状态按照x=[Pd1,Pd2,Pg3,Pg4]T的顺序排列，传统调度控制方法下，系统状态为x=[0.5,2.54,1.0,2.04]T。下面考虑在不同方向进行摄动，计算摄动带来的风险变化，据此求取所研究运行状态处实际的风险梯度。令ΔPd1，ΔPd2和ΔPg3分别在[-0.001,0.001]区间内随机取值，并令ΔPg4=ΔPd1+ΔPd2-ΔPg3，以此方法抽取500组随机摄动，并分别进行风险评估，求取摄动前后后续连锁故障风险之差D。利用计算得到的500组D和[ΔPd1,ΔPd2,ΔPg3,ΔPg4]T进行线性回归，求线性关系式(14)中的系数：

D=γ1ΔPd1+γ2ΔPd2+γ3ΔPg3+γ4ΔPg4

(14)

经过计算，得到：

(15)

而通过本文方法得到的近似风险梯度为：

Γ=[4.229,3.146,-1.06,-0.452]

(16)

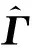
(2)协调控制效果验证

下面在4节点测试系统中验证风险协调优化的效果。首先测试在不同ΔR′取值下系统状态对应的控制成本和连锁故障风险，如图4所示。其中ΔR′=0的点对应不考虑后续连锁故障风险的传统调度方式，即传统DC-OPF模型得到的结果。可见在一定ΔR′的范围内，本文模型能够有效降低连锁故障风险。

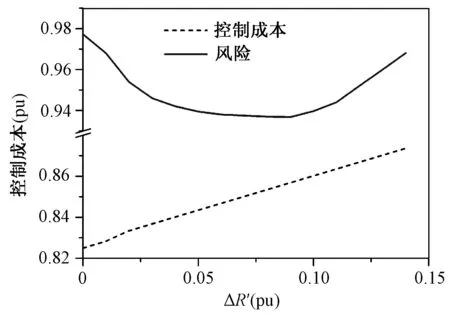
图4 不同ΔR′下的控制成本和连锁故障风险Fig.4 Control costs and cascading outage risks under different ΔR′

图5为控制成本与风险之间的关系。由图4、图5可见，控制成本基本随着ΔR′的增长而线性上升。可见当ΔR′较小时，后续连锁故障风险基本随着ΔR′的增加而线性下降，而当ΔR′增加到一定程度后，风险的下降程度趋缓直至降为0，之后风险反而上升。这说明在ΔR′达到一定程度后，线性化得到的近似风险梯度失效。要获得显著的风险控制效果，需要采用多步迭代控制方法。

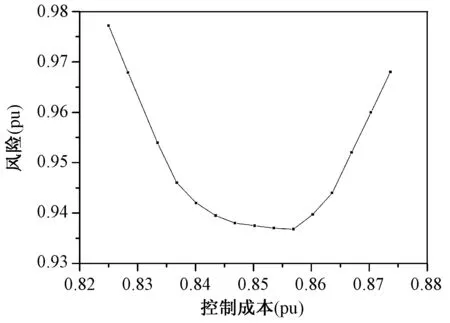
图5 单步协调控制下控制成本与风险的关系Fig.5 Relationship between control cost and risk under single step risk mitigation

图6为多步协调控制下控制成本与风险的关系。由计算结果可见，基于多步迭代的控制方法很好地克服了单步风险控制中线性化近似可能带来的控制误差，通过反复求解近似风险梯度并通过协调优化模型获取更新的控制策略，有效地将后续连锁故障风险降低到接近于0的程度。另外由结果可见，在最初的若干次迭代中，通过相对较小的控制成本即可换取显著的风险下降，然而在风险降低到一定程度后，实现同样程度的风险下降需要付出更多的代价。在实际系统分析中，需要对控制成本和风险进行合理的权衡与协调。尽管付出足够高的控制成本能够充分降低风险，但同时也会降低经济性。因此需要根据实际需求选择合适的运行策略，图6的各点即对应不同经济性、安全性配置的控制策略，可根据实际运行中的风险偏好选取控制策略。假设风险偏好可以用系数λR表示，调度目标为使C0+λRR′尽量小，则λR越大，则调度策略越倾向于降低R′(同时付出更高的控制成本C0)；而λR越小则越倾向于降低运行成本C0(连锁故障风险R′可能相对较高)。在图6所示的结果中，若取λR=1，则应选择C0=1.2141，R′=0.2533的控制策略，而若λR=100，则应选择图6中C0=1.6909,R′=0.0022的控制策略。综上结果和分析可见，本文方法可以灵活用于实际电力系统安全分析，实用性强。

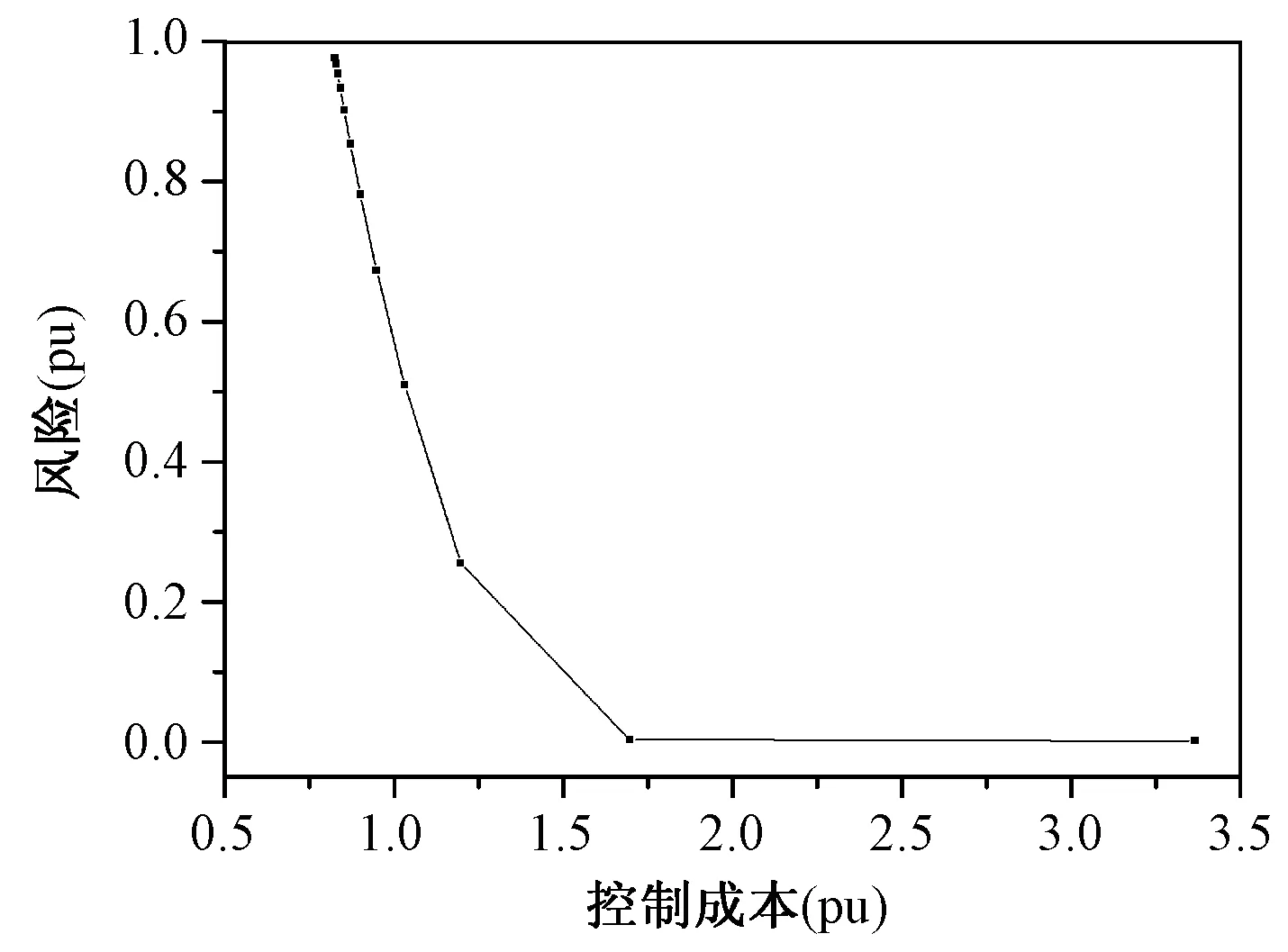
图6 多步迭代控制下控制成本与风险的关系Fig.6 Relationship between control cost and risk under iterative coordinated risk mitigation

5.2 宁夏电网算例分析

下面用较大规模的实际系统来展示本文方法的效果，本节针对宁夏电力系统进行计算分析。宁夏电网系统有148个节点，264条支路，其中发电节点56个，负荷节点61个。由于原系统状态下连锁故障风险很低，将系统负荷调高至原系统的2.5倍，并选取编号为74,99,115,252的四条支路开断为初始故障，进行计算分析。

图7为宁夏电网协调控制的结果。可以看出，经过约20轮迭代后，后续连锁故障风险由20.95下降至13.24，下降了约37%。由此可见本文方法在实际电网连锁故障风险控制方面能够取得较好的效果。然而由于在进行风险梯度计算时简化忽略了系统状态变化对后续各级连锁故障状态以及损失的影响，因而存在一定的误差。该偏差可能导致迭代进行到一定程度后，风险即停止下降。因此为了进一步增强风险控制的效果，下一步工作需要考虑风险控制后系统状态变化对后续各级连锁故障中系统状态、故障概率和损失的影响。

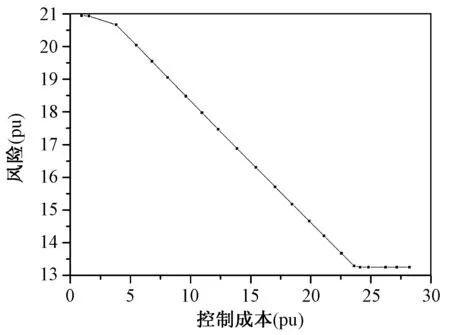
图7 宁夏电网协调风险控制结果Fig.7 Results of coordinated risk mitigation in Ningxia grid case

在计算效率方面，本文方法在Matlab环境中实现，测试环境为便携式计算机(CPU主频2.5GHz，内存4GB)。图7对应的计算过程总共包含22轮迭代，总计算时间约为431.9s，平均每轮迭代控制所用时间约为20s。可见本文方法具有较高的计算效率，若在高性能计算平台上进行计算分析，则有望满足在线分析与辅助决策的需求。如果采用更大的迭代步长和改进的步长控制策略，则有望进一步降低计算时间。另外后续也可以采用交流潮流模型[18]并引入电压稳定性评估[19]，以进一步提高本文方法的准确性和实用性。为了增强本文方法的实用性，还需要研究调度延时、发电机爬坡速度限制等因素对控制效果的影响。本文模型可以进一步扩展，如考虑连锁故障中系统频率特性[20]、HVDC[21]等电力电子元件对风险和控制效果的影响。

6 结论

本文提出了一种协调控制代价与后续连锁故障风险的优化控制方法。基于风险评估得到风险展开式，通过线性化方法近似量化连锁故障风险与初始故障后系统状态的关系，得到连锁故障的风险梯度；建立了风险协调控制优化模型，通过求解模型得到调整发电机有功出力和切负荷策略，在降低风险的条件下最小化运行成本；利用近似风险梯度求解上述优化问题，从而实现了当前控制成本与后续连锁故障风险的协调控制。

针对基于线性化的控制策略计算方法仅在原工作点附近有效的局限性，提出了基于多步迭代的风险协调优化算法。通过风险评估和风险协调优化控制的迭代，逐步搜寻最优控制策略，克服了线性近似的缺点。4节点测试系统和宁夏电网系统算例分析表明，本文提出的风险协调优化控制方法能够有效地降低连锁故障风险，并可实现系统运行经济性与安全性的协调。本文方法能够用于离线预想故障处理预案的计算分析，此外在高性能计算平台上还有望实现实际系统的在线风险分析与辅助控制决策。另外，为了给电力系统提供更加准确、全面的控制决策支持，未来还可以基于交流潮流模型进行建模，考虑连锁故障中的电压稳定性，并考虑加入无功电压控制手段，增强本文方法的实用性。

[1] 梅生伟, 薛安成, 张雪敏(Mei Shengwei, Xue Ancheng, Zhang Xuemin). 电力系统自组织临界特性与大电网安全(Power system self-organized criticality safety features and a large grid)[M]. 北京：清华大学出版社(Beijing: Tsinghua University Press), 2009.

[2] S Mei, Zhang X, Cao M. Power grid complexity[M]. Berlin, Germany: Springer-Verlag GmbH, 2011.

[3] 梅生伟, 薛安成, 翁晓峰, 等(Mei Shengwei, Xue Ancheng, Weng Xiaofeng, et al.). 复杂互联电网大停电风险研究综述及预防控制展望(Summary on risk of blackouts in complex interconnected power grids and prospects of its preventive control)[A]. 第二十四届中国控制会议(24th Chinese Control Conference (CCC))[C]. 广州, 中国(Guangzhou, China), 2005. 180-183.

[4] Vaiman M, Bell K, Chen Y, et al. Risk assessment of cascading outages: Methodologies and challenges[J]. IEEE Transactions on Power Systems, 2012, 27(2): 631-641.

[5] 石立宝, 史中英, 姚良忠, 等(Shi Libao, Shi Zhongying, Yao Liangzhong, et al.). 现代电力系统连锁性大停电事故机理研究综述(A review of mechanism of large cascading failure blackouts of modern power system)[J]. 电网技术(Power System Technology), 2010, 34(3): 48-54.

[6] Yao R, Huang S, Sun K, et al. A multi-timescale quasi-dynamic model for simulation of cascading outages[J]. IEEE Transactions on Power Systems, 2016, 31(4):3189-3201.

[7] Yao R, Huang S, Sun K, et al. Risk assessment of multi-timescale cascading outages based on Markovian tree search[J]. IEEE Transactions on Power Systems, 2017, 32(4):2887-2900.

[8] 姚锐, 黄少伟, 刘锋(Yao Rui, Huang Shaowei, Liu Feng). 考虑发电机励磁保护和OLTC的多时间尺度连锁故障模型(Multi-timescale cascading outage model considering generator excitation protection and OLTC)[J]. 电网技术(Power System Technology),2015, 39(4): 1075-1081.

[9] Wei S, Vittal V. LP-based OPF for corrective FACTS control to relieve overloads and voltage violations[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1832-1839.

[10] Fei X, McCalley J D. Risk based multi-objective optimization for transmission loading relief strategies[A]. IEEE Power Engineering Society General Meeting [C]. Tampa, FL, USA, 2007. 1-7.

[11] Fei X, McCalley J D. Risk-based security and economy tradeoff analysis for real-time operation[J]. IEEE Transactions on Power Systems, 2007, 22(4): 2287-2288.

[12] Yao R, Zhang X, Huang S, et al. Cascading outage preventive control for large-scale AC-DC interconnected power grid[A]. 2014 IEEE PES General Meeting[C]. 2014. 1-5.

[13] 程林, 何剑(Cheng Lin, He Jian). 电力系统可靠性原理和应用(Principles and applictions of power system reliability)[M]. 北京：清华大学出版社(Beijing: Tsinghua University Press), 2015.

[14] 何剑, 程林, 孙元章(He Jian, Cheng Lin, Sun Yuanzhang). 电力系统运行可靠性最优控制(Optimal control of power system’s operational reliability)[J]. 中国电机工程学报(Proceedings of the CSEE), 2010, 30(7): 15-21.

[15] Girgis A A, Mathure S. Application of active power sensitivity to frequency and voltage variations on load shedding[J]. Electric Power Systems Research, 2010, 80(3): 306-310.

[16] Gribik P R, Shirmohammadi D, Hao S, et al. Optimal power flow sensitivity analysis[J]. IEEE Transactions on Power Systems, 1990, 5(3): 969-976.

[17] Dobson I, Carreras B A, Lynch V E, et al. An initial model for complex dynamics in electric power system blackouts[A]. 34th Hawaii International Conference on System Science (HICSS) [C]. 2001.710-718.

[18] 刘巍, 黄少伟, 姚锐, 等(Liu Wei, Huang Shaowei, Yao Rui，et al.). 无功电压特性对连锁故障的影响分析(Effect of reactive power and voltage characteristics on cascading failures)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(9): 64-69.

[19] Yao R, Liu F, He G, et al. Static security region calculation with improved CPF considering generation regulation[A]. 2012 IEEE International Conference on Power System Technology (POWERCON) [C]. 2012. 1-6.

[20] 张振安, 郭金鹏, 张雪敏, 等(Zhang Zhen’an, Guo Jinpeng, Zhang Xuemin, et al.). 考虑频率稳定的大停电事故模型及应用(Blackout model and its application considering frequency stability)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2015, 27(4): 26-32.

[21] Liang Y, Mei S, Liu F, et al. Blackout model for hybrid AC/DC power system[A]. 33rd Chinese Control Conference (CCC) [C]. 2014. 2835-2839.

Cascadingoutageriskmitigationmethodcoordinatingeconomyandsecurityinpowersystems

YANG Chao-ping1, YAO Rui2, ZHANG Shuang1, GU Yu-jia1, SHEN Chen2

(1. Electric power research institute, State Grid Ningxia power grid company, Yinchuan 750001, China)(2. State Key Lab of Control and Simulation of Power Systems and Generation Equipment, Department of Electrical Engineering, Tsinghua University, Beijing 100084, China)

Cascading outages are major threats to the power systems, so it is necessary to realize effective risk mitigation against cascading outages on the basis of cascading outage simulation and risk assessment. This paper proposed a risk mitigation method based on risk assessment results. Firstly, the risk gradient is calculated by linearizing the risk in the space of system states, then the coordinated risk mitigation optimization model is established using the risk gradient. Compared with conventional models, this proposed model can minimize the control cost on the condition that the risk is effectively reduced, thus realizing the coordination between system security and economy. Moreover, to overcome the large errors brought by linearization, an iterative coordinated risk mitigation is further proposed. The test cases on 4-bus test system and on Ningxia Provincial grid verify the effectiveness and efficiency of the proposed method. The method can be utilized in offline control measure analysis against pre-selected contingencies, and it also has potential for online analysis and decision making.

cascading outages; risk; economy; security; coordinated control

2017-01-03

国网宁夏电力公司电力科学研究院科技项目(5229DK14000Z)

杨超平(1963-)， 男， 宁夏籍， 高级工程师， 硕士， 研究方向为电力系统自动化；姚 锐(1989-)， 男， 山东籍， 博士后， 研究方向为电力系统连锁故障分析与防治、 电力系统稳定性分析等。

10.12067/ATEEE1701012

1003-3076(2017)12-0071-08

TM732