轮毂驱动电动汽车差速转向系统仿真分析

赵 琦，时培成，徐增伟

(安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

轮毂驱动电动汽车差速转向系统仿真分析

赵 琦，时培成，徐增伟

(安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

为了研究轮毂驱动电动汽车的差速转向系统，基于Acherman-Jeantand转向模型建立了差速转向解析表达式与仿真模型；给出了电机模型并依据其运动学方程设计了等效滑模速度控制器；搭建出包含差速转向模型、等效滑模控制器、电机模型在内的差速转向控制系统。结合实际工况，在MATLAB/Simulink环境中进行轮毂驱动电动汽车差速转向控制系统的仿真试验并与传统PI控制系统进行仿真对比。仿真试验结果表明：文中所建模型是正确的，控制系统是可行的；体现了等效滑模控制对差速转向系统控制响应时间短、超调量小、鲁棒性强等优势。

轮毂驱动电动汽车；差速转向；等效滑模控制；MATLAB/Simulink；仿真

轮毂驱动电动汽车是近些年受到广泛关注的电动汽车[1]。其将驱动电机固定于轮毂内，无需减速系统，可直接驱动车辆行驶，省略或简化了燃油汽车中大部分传动系统组件。这样不但减轻了整车质量，也提高了整车的可控性。

在轮毂驱动电动汽车研究中，转向系统是主要课题之一[2]。基于这一课题，以自制的轮毂驱动电动汽车为研究对象，构建了轮毂驱动电动汽车差速转向系统。对差速转向模型进行了数学建模并建立了仿真模型。然后给出了电机模型，并依据其运动学方程设计了等效滑模速度控制器对其进行速度环输入控制。最后基于MATLAB/simulink仿真软件进行轮毂驱动电动汽车差速转向控制系统的仿真试验，并与传统PI控制的差速转向系统进行对比。仿真试验结果表明了所建模型是正确的，控制系统是可行的，显示出了等效控制器的诸多特点。

1 差速转向模型

在对四轮毂驱动电动汽车低速转向控制策略的研究中，Acherman-Jeantand转向模型被广泛应用[3]。如图1所示，该模型是车辆的一种理想化行驶状态，需满足几个假设条件：假设车体为刚性；假设车轮做纯滚动；不考虑轮胎的滑移和滑转等。基于此模型，在车辆转向行驶时，四车轮共同以车外一点为圆心做角速度相同的圆周运动。虽然是一种理想化模型，但该模型对四轮毂驱动电动汽车差速转向的研究具有一定的参考价值。因此，可基于此建立四轮毂驱动电动汽车差速转向模型。

其中，O为车辆质心，O`为转向中心，V为车速，V11为左前轮速度，Vr1为右前轮速度，V12为左后轮速度，Vr2为右后轮速度，δ为车辆转向角，δ1为左前轮转向角，δr为右前轮转向角，R0为车辆质心的转向半径，R11为左前轮转向半径，Rr1为右前轮转向半径，R12为左后轮转向半径，Rr2为右后轮转向半径，L为前后轴距，a为车辆质心到前轴距离，b为车辆质心到后轴距离，c为左右轮距。

图1 Acherman-Jeantand转向模型

1.1 推导数学模型

根据图1中的Acherman-Jeantand转向模型，以向左转为例，运用几何知识可以得到以下公式：

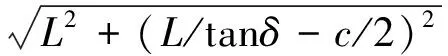
(1)

(2)

Rl2=L/tanδ-c/2

(3)

Rr2=L/tanδ+c/2

(4)

tanδl=L/R3

(5)

tanδr=L/R4

(6)

由以上式(1)～(6)可得左右转向轮转角与车辆转向角的关系式：

tanδl=2L*tanδ/(2L-c*tanδ)

(7)

tanδr=2L*tanδ/(2L+c*tanδ)

(8)

根据瞬心定理可知

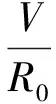
(9)

则有

Vl1=V*Rl1/R0

(10)

Vr1=V*Rr1/R0

(11)

Vl2=V*Rl2/R0

(12)

Vr2=V*Rr2/R0

(13)

又有

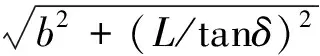
(14)

通过对以上各式的推导可以得到在转向时四车轮速度的解析式：

(15)

(16)

(17)

(18)

对上述诸式进行分析推导不难看出，在车辆进行转向运动时，左右前轮的转角度数与车辆转向角构成一定的几何关系。各车轮速度不仅与当前车速和转向角两个变量有关，还与车辆诸多各参数有关。设计样车各参数取值如表1所示。

表1 样车参数取值

1.2 建立差速转向仿真模型

根据上文所构建的四轮毂电机驱动电动汽车差速转向数学模型，运用MATLAB/simulink软件进行差速转向系统仿真模型的建立。如图2所示，该仿真模型以车速v和车辆转向角δ为输入，以四车轮速度vl1、vr1、vl2、vr2以及左右两转向轮转角δl、δr为输出。

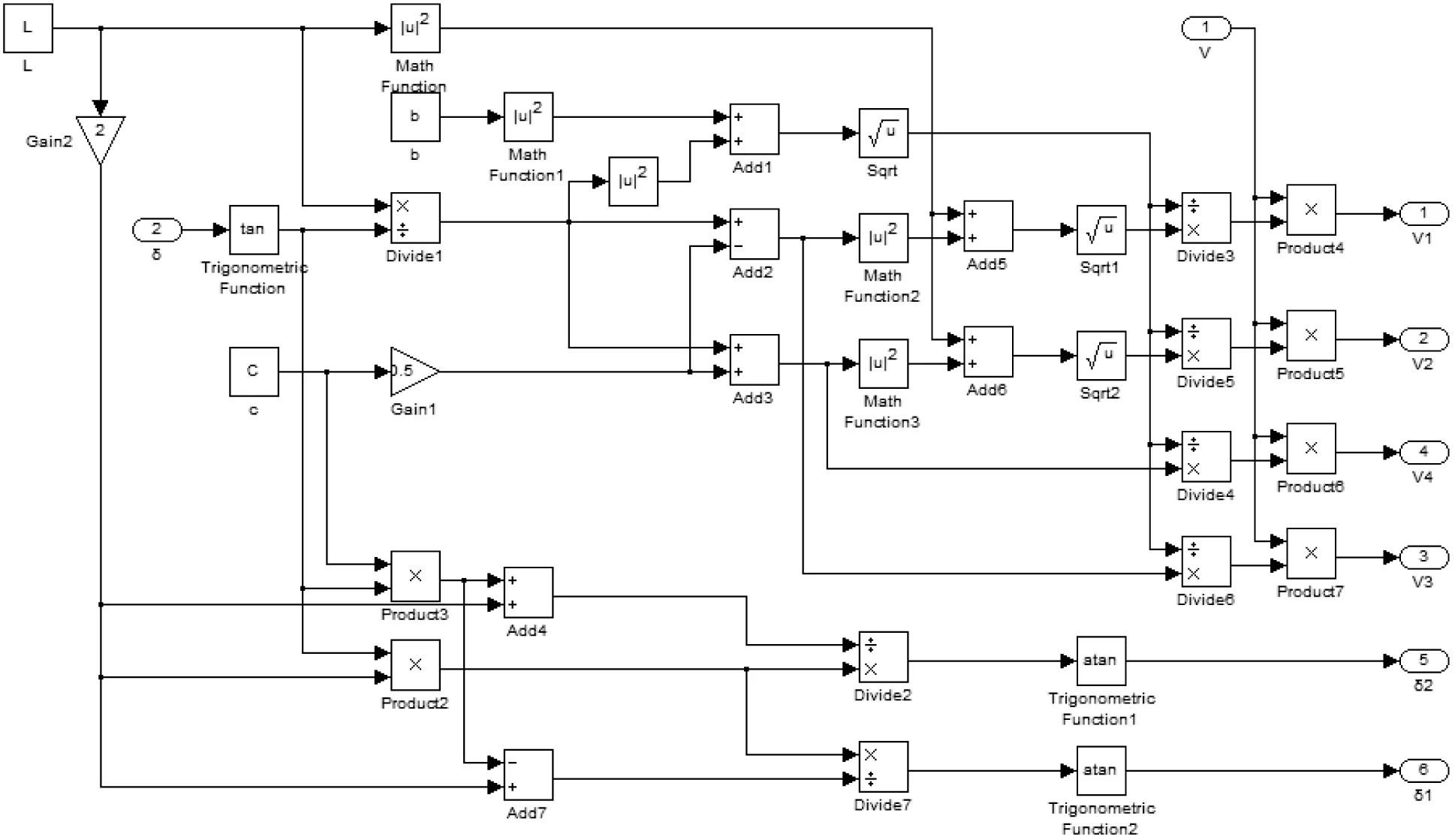
图2 转向差速系统仿真模型

通过对两类模型中的分析不难发现：当车辆转向角δ=0时(即直行工况)，该模型不成立；右转工况的仿真同样需要考虑。为了解决这两种工况的仿真问题，需要对上述差速转向模型进行补充与改进。如图3所示，利用if-else语句完善差速转向模型。

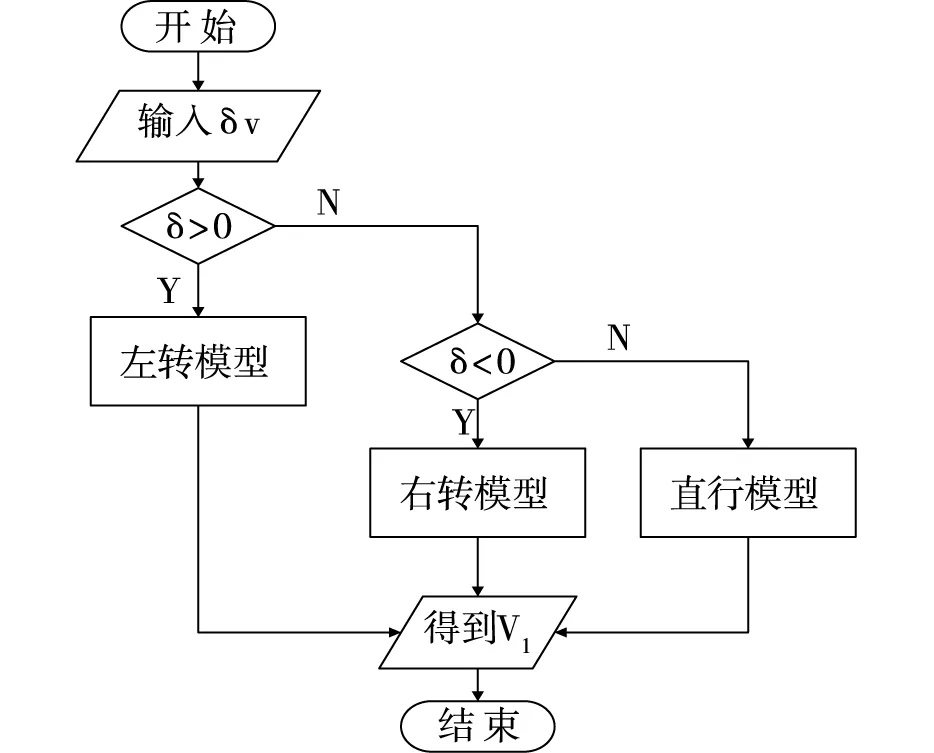
图3 if-else条件语句框图

在MATLAB/simulink仿真软件中运用if模块与if action subsystem模块来实现if-else条件语句功能。如图4所示，以左前轮车速为例，设左转为正，右转为负，并令δ=0时车辆直行。通过if模块对输入的角度变量δ的正负进行判断，而后根据判断结果运用相应模型得到车轮速度。

图4 包含if模块的左前轮车速模型

2 电机模型

由于永磁同步电机(PMSW)拥有较好的启动性能，且其可靠性好，安全性高，额定运行时的效率高[4]，能很好地满足车用驱动电机的要求。此外，此类电机还具有质量轻，体积小，转子发热率低等特点。因此，本文选用永磁同步电机作为研究对象进行控制分析。

2.1 永磁同步电机模型

建立在二相旋转坐标系(d/q)上的PMSW方程为：

(19)

电磁转矩方程为：

(20)

通过上述公式的推导可得系统动力学方程为：

(21)

其中：Ld、Lq为d、q轴电感；ud、uq为d、q轴电压；R为定子绕组的电阻；id、iq为d、q轴电流；p为极对数；ωr为转子角速度；λ为磁链；T为电磁转矩；Te为电磁平均转矩；Tm为机械轴扭矩；F为摩擦系数；J为转动惯量。

2.2 电机控制策略

滑模控制(SMC)具有较强的鲁棒性,能有效改善系统的不确定性。设计合理的滑动模态可使滑模控制系统省略在线辨识过程，实现控制系统快速响应，且相对传统PI控制系统而言，仿真建模较为简单。因此，选用等效滑模控制为永磁同步电机的控制策略较为合理。

由式(20)可知，当Ld=Lq时，

(22)

将式(22)代入系统动力学方程(21)可得

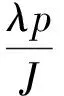
(23)

(24)

设系统扰动为

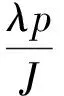
(25)

则式(24)可化为：

(26)

在速度环控制系统中误差计算公式为：

e=ω*-ω

(27)

ω*为差速转向模型的速度输出值，对式(27)求导可得

(28)

2.2.1 滑模面的选取

(29)

其中，c为正常数，取不同的c值，系统可以获得不同的动态性能。

2.2.2 设计等效滑模速度控制器

在设计滑模控制器时，主要有以下两个要求：一是在尽可能短的时间内使速度误差达到滑模面，二是到达后要保证其能够始终维持在滑模面上。为了满足这两个要求，所设计的滑模控制器可以认为是由等效滑模控制部分usq与滑模切换部分usw两部分组成。控制器的输出可表示为：

u=usq+usw

(30)

等效滑模控制部分可以保证系统的状态维持在滑模面上。令s= 0,x(t)=0可得

ueq=ce

(31)

滑模切换控制部分能够确保系统的状态不脱离滑模面。可以将usw设计为式(32)的形式。其中，k是正常数，sign(s) 是符号函数。

usw=ksign(s)

(32)

根据以上分析，设计滑模控制器的控制率为：

(33)

2.3 电机仿真

根据给出的电机解析表达式以所设计的控制策略，在MATLAB/simulink仿真环境下对基于等效滑模控制的永磁同步电机进行模型搭建与分析。如图5所示，在仿真软件中运用Sim Power System Toolbox模型库，依据电机矢量控制原理，建立了包含速度控制等模块的电机仿真模型。

图5 基于等效滑模控制的永磁同步电机仿真模型

图6为电机模型中等效滑模速度控制部分的仿真模型，其输入为差速转向模型提供的车轮转速与电机实际输出的转速只差。输出为提供给模拟电源的电压信号。

图6 速度等效滑模控制结构

电机模型中的各参数设置如表2所示。

表2 电机参数取值

3 仿真实验

在一般情况下，车速是由速度传感器采集的车轮转速计算得来。车速与车轮转速的转换公式为：

(34)

其中：v为车轮车速(m/s)；n为车轮转速(r/min)；r为车轮半径。

结合实际工况，根据所给出的差速模型、电机模型以及电机控制策略，可建立如图7所示的差速转向系统。将采集到的车轮转速转化为速度与转向角一起作为变量输入到差速转向模型，通过模型计算得到四车轮轮速并转化为期望转速与电机实际转速做差输入到等效滑模控制器，以控制各车轮电机运行并驱动车辆行驶。

图7 差速转向系统原理图

3.1 变角度仿真蛇形行驶

为结合实际，在仿真蛇形行驶实验中将车辆速度输入量设为100RPM，车辆转向角输入为如图8所示在[-π/4, π/4]之间峰值变化的角度值。以此验证所建差速系统的可行性，并与传统PI控制的系统进行对比，论证等效滑模控制对系统有更优的控制效果。

图8 转向角随时间变化情况

3.2 仿真分析

根据所设计的仿真试验要求，对四车前轮转速进行仿真并得到如图9所示结果。通过分析可知，在转向时内侧车轮转速小于外侧车轮转速，这与实际情况相符。验证了所建差速转向控制系统的正确性。在转向角度不断变化时，车辆可以通过差速转向系统控制各车轮速度实现转向行驶。证明了差速转向控制系统实现车辆转向行驶的可行性。

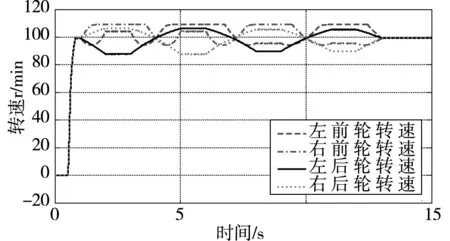
图9 两前轮转速

以左前轮为例，进行等效滑模控制与传统PI控制差速转向系统的比较试验。由图10所示仿真结果可知，等效滑模控制的左前轮转速的响应时间变短，有效减弱了超调现象，降低了超调量，显著控制了转速的变化幅值，增强了系统鲁棒性。验证了等效滑模控制能更好地控制轮毂驱动电动汽车差速转向系统。

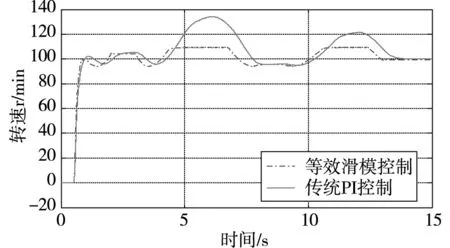
图10 等效滑模控制与传统PI控制对比仿真结果

结论

轮毂驱动电动汽车在经济性、整车控制等方面体现出了诸多优势，是汽车的未来发展方向之一。差速转向技术是其重要性能指标之一，差速转向系统的好坏影响着车辆的操纵稳定性和行驶平顺性。因此，对差速转向的不断探究是非常必要的。

以自制的轮毂驱动电动汽车为研究对象，给出了差速转向解析表达式并在MATLAB/simulink环境下建立了差速转向仿真模型；进行了永磁同步电机的模型建立并根据其运动学方程设计了等效滑模速度控制器。根据实际工况，进行了蛇形行驶仿真实验。通过对所得仿真结果的分析，验证了所建系统的正确性与可行性；通过与传统PI控制差速转向系统对比，体现了等效滑模控制对差速转向系统控制响应时间短、超调量小、鲁棒性强等优势。

尽管通过试验和分析得到了一些理论成果，对今后差速转向系统的研究工作有一定的参考价值，但本文并未涉及转矩控制领域，对样车平顺性也未做考虑。这将成为之后研究的方向。

[1]Ma Xiaojun，Su Jianqiang，Xiang Yu，Ji Xiangpu, Hou Mingjie.Co-simulation research of in-wheel motor drive vehicle steering control[J].Applied Mechanics & Materials，2013(415)：578-581.

[2]宋龙龙，郑培，范满珍.四轮毂电动机独立驱动电动车转向策略的试验[J].上海电机学院学报，2015(06)：331-336.

[3]董铸荣，贺萍，朱小春.基于Ackermann模型的轮毂电机四轮独立驱动电动汽车电子差速转向控制研究[J].深圳职业技术学院学报，2013(05)：26-29.

[4]宋舒,龚建国,林薇,汪贵平.纯电动汽车用永磁同步电机空间矢量控制系统建模与仿真[J].武汉理工大学学报，2012(04)：118-122+140.

[5]王涛，李勇，王青，贾克军.永磁同步电机矢量控制系统建模与仿真[J].河北大学学报(自然科学版)，2011(06)：648-652.

[6]张晓光，孙力，赵克.基于负载转矩滑模观测的永磁同步电机滑模控制[J].中国电机工程学报，2012(03)：111-116+8.

[7]Leng Bo，Xiong Lu， Jin Chi，Liu Jun，Yu Zhouoing.Differential Drive Assisted Steering Control for an In-wheel Motor Electric Vehicle[J].SAE International Journal of Passenger Cars - Electronic and Electrical Systems，2015，8(2).

[8]靳彪，张欣，杨庆保.纯电动汽车低速转向差速控制模型[J].北京交通大学学报，2013(04)：158-161.

[9]邹权，钱林方，蒋清山.永磁同步电机伺服系统的自适应模糊滑模控制[J].控制理论与应用，2015(06)：817-822.

[10]皇甫宜耿，S.Laghrouche，刘卫国，A.Miraoui.一种高阶滑模控制的永磁同步电机磁通和电阻辨识[J].西北工业大学学报，2010(05)：684-688.

SimulatedAnalysisforDifferentialSteeringSystemofIn-wheelMotorElectricVehicle

Zhao Qi, Shi Peicheng, Xu Zengwei

(School of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu, Anhui 241000, China)

To study the differential steering system of In-wheel Motor electric vehicles, the differential resolution expression and simulation model were established based on the Acherman-Jeantand steering model. The motor model was given and an equivalent sliding mode speed controller was designed based on its kinematics equation. The control system of differential steering was constructed, including differential steering model, equivalent sliding mode controller and motor model. Combined with the actual condition, the simulation test of the difference speed steering control system of the In-wheel Motor electric vehicle, which compared with the traditional PI control system, was simulated in the MATLAB/Simulink environment. The simulation results show that the model is correct and the control system is feasible. It shows that the equivalent sliding mode control has the advantages of shortening response time, reducing overshoot and enhancing robustness for the differential steering system.

in-wheel motor electric vehicle; differential steering; Equivalent sliding mode control; MATLAB/Simulink; simulation

ClassNo.:U463.4:U469.72DocumentMark：A

宋瑞斌)

赵琦，硕士，安徽工程大学。研究方向：汽车电子。时培成，博士，教授，安徽工程大学。徐增伟，硕士，安徽工程大学。研究方向：新能源汽车。

国家自然科学基金项目(编号：51575001)；安徽省科技攻关计划项目(编号：1604a0902158)。

2096-3874(2017)12-0034-07

U463.4:U469.72

A