一类p-基尔霍夫方程的正解
2017-12-23刘峰霞张建明王淑丽郭祖记
刘峰霞, 张建明, 王淑丽, 郭祖记
(太原理工大学 数学学院, 山西 太原 030024)
一类p-基尔霍夫方程的正解
刘峰霞, 张建明, 王淑丽, 郭祖记
(太原理工大学 数学学院, 山西 太原 030024)
利用变分方法研究了RN上带有势函数的p-基尔霍夫型方程正解的存在性. 首先证明该问题的能量泛函存在(C)c序列, 然后由(C)c序列的有界性, 径向对称空间和势函数的性质证明此(C)c序列具有收敛子列. 因而证明了该问题至少存在一个非平凡解, 最后证明此平凡解是正解.
p-基尔霍夫方程; (C)c序列; 山路引理; 正解
0 引 言
本文将考虑如下p-基尔霍夫型方程
正解的存在性, 其中a>0,b≥0是常数, -Δpu=-div(|u|p-2u)是p-拉普拉斯算子,N≥3, 1 f1)f∈C(R,R+),f(s)=0,s≤0. m=F(r),μF(s)-f(s)s≤κs2, ∀s≥r. α2) 存在ρ>0 和β∈ (0,|α|∞), 使得meas[Bρ(0)α-1(β,+∞) ]=0且 ∀x∈RN. 当p=2时, 问题(P)和下面的方程 有关, 它是被Kirchhoff[1]作为经典的D’Alambert波动方程提出来的. 一些关于Kirchhoff方程的早期的经典研究[2-3], 直到Lions[4]对方程(1)提出了一个抽象的框架之后, 问题(1)才受到了广泛关注. 一些有关问题(1)的其他结论[5-7]. 很多作者[8-10]在全空间研究了方程 解的存在性和多重性. 受文献[11]的启发, 本文讨论在f1)~f5)和α1)~α2)的假设条件下, 问题(P)的正解存在性, 且证明方法和文献[11]有所不同. E u(x) =u(|x|)}. 由Sobolev嵌入定理, 对q∈[p,p*], 嵌入W1,p(RN)⊂Lq(RN)是连续的, 即存在γq>0, 使得 |u|q≤γq‖u‖, ∀u∈W1,p(RN), 式中: |·|q表示Lq(RN)中的范数. 定义泛函I∶E→R为 显然,I∈C1(E,R), 且 〈I′(u),v〉= 则I在E中的临界点是问题(P)的解. 定理1[12]设E是一个Banach空间,E*是它的对偶空间,I∈C1(E,R). 若存在正数ζ,η,ρ和点e∈E, 满足‖e‖>ρ且 Γ∶={γ∈C([0,1],E)∶γ(0),γ(1)=e}, 则存在一个序列{un}⊂E满足 I({un})→c≥η, 这种序列通常被称为(C)c序列. 引理1 存在ρ,η>0, 使得对一切满足‖u‖=ρ>0 的u, 有I(u)≥η. 证明由f2)和f4)知, 任给ε>0, 存在A=A(ε,θ), 使得 f(s)≤ε|s|p-1+A|s|θ-1, 结合式(2), 式(3)和式(6), 有 I(u)≥ 引理2 在f3)条件下, 存在e∈E使得‖e‖>ρ且I(e)<0. 结合f3)及式(7)可知, 由f2})和式(8)得, 任给M>0, 存在C1=C1(M,τ)>0, 使得 定义函数 引理3 若{un}⊂E满足式(5), 则{un}有界. wn⇀w在E上;wn→w在Lσ(RN)上,σ∈(p,p*);wn(x)→w(x) a.e.x∈RN. 记Ω±∶={x∈RN∶±w(x)>0}, 则由式(8)可得 a.e.x∈Ω+. 另一方面, 由 可得 再由Fatou引理, 有 因此, meas(Ω+)=0. 又式(5)蕴含 结合f5), 有 pI(tun)≤pI(tnun)-〈I′(tnun),tnun〉= ∀t∈[0,1]. 由式(5)可知I(un)=c+o(1), 〈I′(un),un〉=o(1). 所以, 若tn=1, 则pI(tun)≤pI(un)=pc+o(1), ∀t∈[0,1]. 故式(11)也成立. 另一方面, 由于嵌入E⊂Lθ(RN)是紧的, 故在Lθ(RN)上,wn→0. 结合式(6),α1)以及Hölder不等式可知, 任取R∈R+, |wn|p+ 因此, 结合式(11)和式(12)可得, 若R→+∞, 这是一个矛盾, 所以{un}有界. 引理得证. 定理2 若f1)~f5)及α1)~α2)成立, 则问题(P)至少有一个正解u∈E, 满足I(u)>0. 证明由引理 1, 引理2和定理1得, 存在{un}⊂E满足式(5), 其中 Γ={γ∈C([0,1],E)∶γ(0)=0,γ(1)=e}. 又由引理3可知{un}有界, 故存在u∈E使得 un⇀u在E上,un→u在Lθ(RN)上, 下证在E上,un→u. 由式(5)和式(15)可得 o(1)=〈I′(un)-I′(u),un-u〉= 再由式(6), Young不等式和Hölder不等式可知 |un|p-1|un-u|+A|un|θ-1|un-u|)≤ 结合式(15), 式(1)和{‖un‖}的有界性得, 同理 任取ξ,η∈Rn,n∈N, 由不等式[13] (|ξ|p-2ξ-|η|p-2η)(ξ-η)≥ 由式(16)~式(21)可得, 所以, 即在E上,un→u. 进一步, 有I(u)=c,I′(u)=0. 由f1)和〈I′(u),u-〉=0得u-=0, 即u(x)≥0. 再由Harnack不等式知u(x)>0对于所有的x∈RN都成立, 故定理得证. [1] Kirchhoff G. Mechanik[M]. Leipzig: Teubner, 1883. [2] Pokhozhaev S I. On a class of quasilinear hyperbolic equations[J]. Matematicheskii Sbornik, 1975, 138(1): 152-166. [3] Bernstein S. Sur une classe d’équations fonctionnelles aux dérivées partielles[J]. Izv. Akad. Nauk SSSR Ser. Mat, 1940, 4(1): 17-26. [4] Lions J L. On some questions in boundary value problems of mathematical physics[J]. North-Holland Mathematics Studies, 1978, 30: 284-346. [5] Arosio A, Panizzi S. On the well-posedness of the Kirchhoff string[J]. Transactions of the American Mathematical Society, 1996, 348(1): 305-330. [6] Cavalcanti M M, Domingos Cavalcanti V N, Soriano J A. Global existence and uniform decay rates for the Kirchhoff-Carrier equation with nonlinear dissipation[J]. Advances in Differential Equations, 2001, 6(6): 701-730. [7] D’Ancona P, Spagnolo S. Global solvability for the degenerate Kirchhoff equation with real analytic data[J]. Inventiones Mathematicae, 1992, 108(1): 247-262. [8] He Xiaoming, Zou Wenming. Existence and concentration behavior of positive solutions for a Kirchhoff equation inR3[J]. J. Differential Equations, 2012, 252(2): 1813-1834. [9] Li Gongbao, Ye Hongyu. Existence of positive ground state solutions for the nonlinear Kirchhoff type equations inR3[J]. J. Differential Equations, 2014, 257(2): 566-600. [10] Liu Zhisu, Guo Shangjiang. On ground states for the Kirchhoff-type problem with a general critical nonlinearity[J]. J. Math. Anal. Appl., 2015, 426(1): 267-287. [11] Ge Bin, Zhou Qingmei, Zu Li. Positive solutions for nonlinear elliptic problems ofp-Laplacian type onRNwithout (AR) condition[J]. Nonlinear Anal: Real World Appl., 2015(21): 99-109. [12] Ekeland I. Convexity methods in Hamiltonian mechanics[M]. Berlin: Springer-Verlag, 2012. [13] Júlio F, Corrêa S A, Figueiredo G M. On an elliptic equation of p-Kirchhoff type via variational methods[J]. Bulletin of the Australian Mathematical Society, 2006, 74(2): 263-277. PositiveSolutionofthep-KirchhoffEquation LIU Feng-xia, ZHANG Jian-ming, WANG Shu-li, GUO Zu-ji (College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China) The existence of positive solutions forp-Kirchhoff-type equation with a potential function onRNwas investigated by using variational methods. Firstly, (C)csequence of the energy functional corresponding to the equation was obtained. Secondly, it was demonstrated that the (C)csequence contained the convergent subsequence through the boundedness of the sequence, the property of radial symmetry space and the assumptions of the potential function, and then the problem (P) has at least one nontrivial solution. Finally, it draws the conclusion that the nontrivial solution is positive. p-Kirchhoff equation; (C)csequence; mountain pass theorem; positive solution 1673-3193(2017)05-0513-05 2016-04-18 山西省自然科学基金资助项目(201601D102001) 刘峰霞(1991-), 女, 硕士生, 主要从事非线性泛函分析研究. O175 A 10.3969/j.issn.1673-3193.2017.05.002





1 预备知识











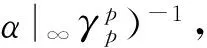







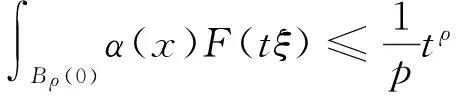








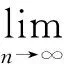









2 主要结论