基于OBE-ELM的球磨机料位软测量
2017-12-23程瑞辉阎高伟
程瑞辉, 阎高伟
(太原理工大学 信息工程学院, 山西 太原 030600)
基于OBE-ELM的球磨机料位软测量
程瑞辉, 阎高伟
(太原理工大学 信息工程学院, 山西 太原 030600)
针对采用传统极限学习机在球磨机料位软测量建模过程中, 存在鲁棒性差, 预测精度不高等缺点, 提出一种基于最优定界椭球(Optimal Bounding Ellipsoid, OBE)改进极限学习机(Extreme Learning Machine, ELM)的建模方法. 该方法以球磨机振动信号为观测变量, 采用偏最小二乘法提取有效特征, 将提取到的有效特征输入到ELM中进行模型训练, 并利用OBE在模型误差未知但有界的条件下, 对网络权值进行约束优化. 通过小型球磨机实验表明, 在对球磨机料位进行回归预测时, 该方法的评价指标与其它方法相比有所提高, 测量结果的箱线图也直观展示该方法具有更好的鲁棒性.
球磨机料位; 软测量; 最优定界椭球; 极限学习机
0 引 言
球磨机作为一种基础破磨设备, 广泛应用于冶金、 电力及化工等行业. 其经济性与内部料位相关, 料位过低导致当前工作效率低, 能源利用率不高, 料位过高容易造成球磨机堵磨, 存在安全隐患. 因此, 准确地测量料位对球磨机的优化控制具有重要意义.
近年来, 科研人员针对球磨机料位的测量提出了多种软测量模型. 文献[1]对球磨机振声信号进行希尔伯特变换(Hilbert Transformation, HT), 并提取有效特征训练BP神经网络. 文献[2] 采用傅里叶变换(Fast Fourier Transform, FFT)将振动信号从时域转换成频域, 并利用深度信念网络(Deep Belief Network, DBN)提取特征训练极限学习机(Extreme Learning Machine, ELM), 建立料位与振动信号相对应的关系模型. 文献[3]提出一种基于筒体振动的选择性极限学习机集成方法, 利用核主元分析算法(Kernel Principal Component Analysis, KPCA)提取信号的频谱特征, 最后采用ELM建立软测量模型.
作为神经网络中的一种, 极限学习机本质上是单隐含层前馈神经网络[4]. 在训练过程中只需要设置隐含层的节点个数, 对输入层和隐含层之间的输入权值以及隐含层的偏置随机初始化, 便可通过计算隐含层输出矩阵的广义逆得到唯一的最优解. 相对于BP神经网络, 具有训练速度快和泛化性好的优点. 但是, 由于缺乏有效的训练方法, 使得其在预测过程中随机性较大, 预测结果不稳定[5]. 针对该问题, 文献[6]采用遗传算法(Genetic Algorithm, GA)优化输入层和隐含层的连接权值、 隐含层的偏置、 输入变量以及隐含层的结构, 从而达到优化ELM的目的. 文献[7]首先初始化一个极限学习机模型, 在训练过程中, 逐步增加隐含层神经元的个数, 并调整输出权值, 直到模型的训练误差小于误差阈值为止. 文献[8]采用主成分分析(Principal Component Analysis, PCA)对ELM隐含层进行降维得到列满秩的新矩阵, 从而解决模型中多重共线性的问题, 进而优化模型.
集员估计是在给定数据集, 模型结构以及噪声边界的条件下, 描述模型的可行参数集合. 该集合内的参数可看作是对模型参数辨识时的有效参数[9]. 在集员估计理论中, 最优定界椭球(Optimal Bounding Ellipsoid, OBE)是其中的经典算法之一. 文献[10]采用OBE训练传统神经网络的权值, 实现非线性系统参数辨识. 文献[11]采用具有时变因子的指数加权(Recursive Least-Squares, RLS)对OBE算法进行改进, 使其具有更好的收敛性和跟踪性能. 基于此, 本文将OBE应用到ELM中, 对其参数进行优化.
综上, 本文将最优定界椭球优化算法引入极限学习机, 建立软测量模型. 通过UCI数据集及实验室球磨机进行实验, 表明建立的软测量模型具有较好的测量精度. 该方法成本低, 且不受水质及弹丸空泡影响, 但其不能测量着靶姿态, 并且速度测量精度易受线圈缠绕一致性、 着靶偏移量以及过靶姿态等因素影响.
为满足野外恶劣水质环境下同时测量弹丸着靶位置、 姿态和速度的工程需要, 本文运用磁偶极子理论提出了基于磁梯度靶的水下弹道测试原理, 在此基础上, 结合PSO-Newton混合算法设计了弹道着靶参数解算方法. 最后, 以某型水下枪弹为例进行仿真射击实验, 并对其测量误差进行讨论, 分析结果验证了该解算方法的有效性.
1 理论与算法
1.1 极限学习机


式中:Wl×n表示隐含层与输入层的权值矩阵;βm×l表示输出层与隐含层的权值矩阵;bl×q表示q个样本的隐含层偏置;φ(·)表示隐含层的激活函数, 一般选择Sigmoid函数. 在模型训练过程中总存在一组β,W和b, 使得SLFN的输出无限逼近于期望输出, 即

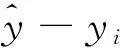
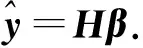


通过求式(3)的最小二乘解可以获得
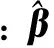
1.2 最有定界椭球算法
非线性系统的状态方程和量测方程分别为

式中:x(t)∈Rn表示第t时刻的状态向量;A(t)∈Rn×n为状态转移矩阵;a(t)∈Rn为状态噪声向量;H(t)∈Rm×n为测量矩阵;y(t)∈Rm表示观测向量;b(t)∈Rm为测量噪声向量. 假设噪声未知但有界, 包含噪声a(t)和b(t)的椭球集合分别为D(t) 和V(t), 具体表达式为


式中:M为状态噪声椭球集合的半正定矩阵.
1.2.1 状态更新
根据椭球学习算法[12],t时刻的状态可行集为
E(t)=

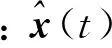
A(t-1)x(t-1)⊕a(t-1).
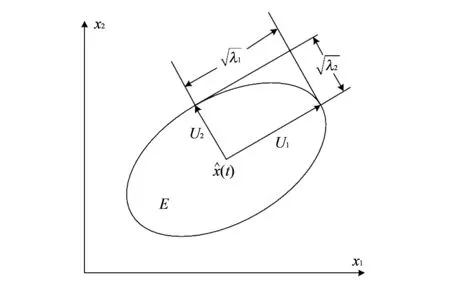
图 1 椭球模型图Fig.1 Ellipsoid model diagram
此时外定界椭球为
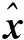

按照最小迹椭球定理[13], 外定界椭球E(t|t-1)的半正定矩阵P(t|t-1)满足非线性方程
P(t|t-1)=
(1+1/p(t-1))A(t-1)P(t-1)AT(t-1)+

1.2.2 量测更新
测量集合为

而此时递推算法[14]为
K(t)=λ(t)p(t)HT(t)=P(t|t-1)HT(t)·




σ2(t)=

1.3 OBE-ELM模型
传统的极限学习机在训练网络时, 输入权值是随机的初始化, 然后再根据隐含层的输出矩阵, 利用最小二乘法计算网络的输出权值. 因此, 网络预测的准确性在一定的程度上也取决于输入层权值的初始化, 从而造成传统的极限学习机在预测的时候存在很大的随机性和预测结果的不稳定性. 而最优椭球定界算法能够在给定误差边界的条件下, 不断地优化模型参数. 所以, 将椭球定界算法用在传统的极限学习机中可以在给定误差边界的条件下, 适当地对极限学习机的输入权值进行约束, 使得其降低模型的随机性, 提高预测结果的稳定性.
此外, 在文献[8-12]中, 辨识的系统均为离散的非线性方程, 即在模型预测时通过k时刻的x预测同一时刻的y. 因此, 利用OBE优化非线性系统时, 是逐个输入训练样本. 而在实际的工业过程中, 样本数据都是成批的, 这就要求在训练模型过程中实现批处理. 所以, 在本文的OBE-ELM模型中, 将求出成批样本标签与当前网络权值的函数关系, 从而实现批处理, 来满足实际工业过程的需求.
对于多输入单输出的ELM模型, 式(1)可以改写为

在网络模型训练过程中, 网络权值随着样本输入的变化而变化. 基于此, 可以将网络权值放在一维向量中作为自变量, 对应的网络输出为因变量, 具体的原理如图 2 所示, 而式(19)通过线性化可以表示为

考虑到在进行网络模型训练时, 批处理样本的个数为q, 所以, 在对权值向量θ求偏导时, 采用雅可比行列式
式中:n表示网络模型权值的个数. 这样可以得到关于ELM模型的量测方程.

图 2 OBE-ELM原理图Fig.2 The principle diagram of OBE-ELM
OBE-ELM算法程序如下:
输出: 修正后的权值θ.
Step1: 设置隐含层节点数:l=l(0).
Step2: 随机生成权值和偏置:W(0)和b(0).
Step3: 输出权值为β(0)=[φ(W(0)x+b(0))]+y.
Step4: 初始化权值向量θ(0)=[W(0),b(0),β(0)].
Step5: 初始化P(0)=diag(lenth(θ(0))).
Step6: 设置转移矩阵A(0)=ones(length(θ(0))).
Step7: fort=1 tom.
根据式(11)计算: (P(t-1),A(t-1))⟹P(t|t-1),


H(t)=, G(t)=H(t)P(t|t-1)HT(t), g(t)=max(SVD(G(t))),
if:δ(t)>γ
λ(t)=(1/g(t))×‖δ(t)‖/(γ-1)
根据式(14)~式(18)计算
(P(t|t-1),λ(t),H(t))⟹K(t)
(K(t),δ(t),θ(t-1)⟹θ(t|t-1)
(P(t-1),K(t-1),H(t-1))⟹P(t)
(θ(t|t-1),λ(t),H(t),P(t),δ(t))⟹θ(t)
s(t)=1+λ(t)g(t)
(s(t),λ(t),σ(t|t-1)⟹σ(t)
End if
End for
2 实验结果及分析
2.1 UCI数据集
本文利用来自University of California at Irvine (UCI) Machine Learning Repository的标准数据集对OBE-ELM模型进行测试, 分别是Housing, Concrete Compressive Strength (CCS)和Energy Efficiency (EE). 辅助设备精确标定. 其具体的数据集描述如表 1 所示.

表 1 UCI数据集描述Tab.1 UCI datasets description
为了验证所建立的OBE-ELM软测量模型的有效性, 将其与传统的极限学习机ELM及最优剪枝极限学习机(Optimally Pruned Extreme Learning Machine, OPELM)[15]、 在线序列极限学习机(Online Sequential Extreme Learning Machine, OSELM)[16]、 PELM(PCA-ELM)[17]进行对比. 采用如下测量结果评价模型性能: 均方根误差(Root Mean Square Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)
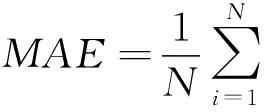
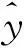
UCI数据集的测量结果如表 2 所示, 其中y1和y2表示ENB 数据集的两个输出. 从表 2 中可以看出OBE-ELM在UCI数据集中的RMSE值和MAE值比传统的ELM及其改进算法的预测误差都小, 由此可见, 利用OBE算法训练ELM 神经网络的权值有显著的效果, 预测精度也得到明显的提升.

表 2 不同数据实验结果对比表Tab.2 Different datasets’ result comparison
2.2 球磨机实验
球磨机实验中, 在钢球装载量和电机转速保持不变的情况下, 每增加1 L料位, 采集该料位对应的60 s振动信号直到达到20 L料位. 实验结束时, 一共采集了20组实验数据, 将每组实验数据分成22个样本, 其中15个样本用来做训练, 7个样本用来做测试, 所以最后得到训练集样本数为20×15=300个, 测试集样本数为20×7=140个. 实验采集的球磨机振动信号经过Welch方法求取功率谱, 分析发现振动信号的有效范围为60~6 000 Hz, 以20 Hz 为单位进行分割并求平均值, 得到每个样本的维度为(6 000-600)÷20=270. 然后通过PLS 算法提取有效特征, 使样本维度从270维降低到10维. 最终球磨机数据训练集为300×10, 测试集为140×10.
图 3 给出了PLS, OBE, ELM相互结合的软测量模型. 模型输入是传感器采集的球磨机振动信号. 首先利用Welch方法求取功率谱, 然后利用PLS提取频谱特征的有效特征值, 最后将提取的有效特征值送入到OBE-ELM进行建模并预测. 在对模型性能进行验证时, 采用与UCI数据集相同的评价函数RMSE和MAE, 如式(22)和式(23).
在网络模型中, 隐含层节点个数是一个重要参数, 因此球磨机实验中采用网格搜索算法对ELM, OPELM, OSELM, PELM以及OBE-ELM模型参数进行寻优. 通过网格寻优得到的最优参数以及10次测量结果的平均值如表 3 所示.

图 3 软测量模型图Fig.3 Soft measurement model diagram表 3 模型参数Tab.3 Model parameters

模型参数测量结果MAERMSEELMNhidden=500.58420.7703OPELMNhidden=900.46150.5838OSELMNhidden=60,Ndata=1500.50970.7096PELMNhidden=2500.59910.7648OBE-ELMNhidden=20,γ=1.70.37710.5017
图 4 给出10次测量结果的RMSE和MAE的箱线图. 图 5 中给出了ELM, OPELM, OSELM, PELM以及OBE-ELM等不同方法最优预测的结果.

图 4 测量结果的箱线图Fig.4 Box-plot of measurement result

图 5 不同测量方法的最优结果Fig.5 Optimal results of different measuring methods
表 3 中Nhidden表示隐含层神经元的个数;Ndata表示初始化OSELM模型时输入样本的个数;γ为OBE-ELM模型中误差阈值. 从表中可以看出, 除PELM外, 其他ELM改进算法的平均RMSE和平均MAE比传统ELM都明显降低. 而基于OBE的ELM 模型则优于传统的ELM及其他改进算法的模型, 其预测结果是最好的.
由图 4 可以看出, ELM, OP-ELM, OS-ELM, PELM的稳定性不好, 且测量精度不高. 而采用OBE-ELM模型的方法, 不仅具有较高的测量精度, 而且其稳定性也得到很好的改善, 说明在OBE-ELM模型中, OBE对权值的初始化起到一定的约束能力, 从而降低模型的随机性, 达到稳定的效果.
从图 5 可以看出, ELM, OS-ELM, PELM方法的测量曲线在中、 低料位段的跟踪性较差,从而造成最终的预测精度不高; 与它们相比, OP-ELM方法测量曲线的跟踪性在低料位段有所改善, 但是中料位段的跟踪性依旧较差, 因此预测精度相对前三种方法有所提高; OBE-ELM方法在低料位段和中料位段的跟踪效果与其它方法相比优势比较明显, 且测量精度也是最高的, 验证了OBE-ELM 模型具有良好的预测能力.
3 结 论
针对极限学习机在软测量建模中, 存在的精度不高、 预测结果不稳定等缺点, 本文提出了基于集员估计的极限学习机软测量建模方法, 采用椭球定界算法优化网络模型参数, 并给出了算法理论推导以及程序流程, 最后应用于UCI数据集和小型球磨机的建模预测中. 实验结果表明, 本文提出的算法在误差未知但有界的条件下, 能使模型参数随着迭代次数的增加而得到优化, 有效解决了预测结果具有一定随机性的缺点, 提高了模型预测准确度. 在下一步工作中, 考虑将其应用在多输出模型中, 并实现在线软测量.
[1] 沙毅, 曹英禹, 郭玉刚. 磨煤机振动信号分析及基于BP网的料位识别[J]. 东北大学学报(自然科学版), 2006, 27(12): 1319-1323.
Sha Yi, Cao Yingyu, Guo Yugang. Analysis of acoustic signal and BP neural network-based recognition of level of coal in ball mill [J]. Journal of Northeastern University (Natural Science), 2006, 27(12): 1319-1323. (in Chinese)
[2] 康岩, 卢慕超. 基于DBN-ELM的球磨机料位软测量方法研究[J]. 仪表技术与传感器, 2015, 27(4): 73-75.
Kang Yan, Lu Muchao. Soft sensor for ball mill fiil level based on DBN-ELM model [J]. Instrument Technique and Sensor, 2015, 27(4): 73-75. (in Chinese)[3] 赵立杰, 汤健, 柴天佑. 基于选择性极限学习机集成的磨机负荷软测量[J]. 浙江大学学报, 2011, 45(12): 2088-2092.
Zhao Lijie, Tang Jian, Chai Tianyou. Soft sensor of mill load based on selective extreme learning machine ensemble[J]. Journal of Zhejiang University, 2011, 45(12): 2088-2092. (in Chinese)
[4] Huang G B, Wang D H, Lan Y. Extreme learning machines: a survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122.
[5] Pacifico L D S, Ludermir T B. Evolutionary extreme learning machine based on particle swarm optimization and clustering strategies[C]∥Neural Networks (IJCNN), The 2013 International Joint Conference, 2013: 1-6.
[6] Tiago Matias, Rui Araújo. Genetically optimized extreme learning machine[C]∥Emerging Technologies and Factory Automation (ETFA), Cagliari, 2013: 1-8.
[7] Feng G, Huang G B, Lin Q, et al. Error minimized extreme learning machine with growth of hidden nodes and incremental learning[J]. IEEE Transactions on Neural Networks, 2009, 20(8): 1352-1357.
[8] Zhang H G, Yin Y X, Zhang S. An improved ELM algorithm for the measurement of hot metal temperature in blast furnace[J]. Neurocomputing, 2016, 22(6): 232-237.
[9] Rubio J D J, Yu W, Ferreyra A. Neural networks training with optimal bounded ellipsoid algorithm[J]. Neural Computing and Applications, 2009, 18(6): 623-631.
[10] 王魏, 邓长辉, 赵立杰. 椭球定界算法在混合建模中的应用研究[J]. 自动化学报, 2014, 40(9): 1875-1881.
Wang Wei, Deng Changhui, Zhao Lijie. Research of ellipsoid bounded algorithm in hybrid modeling[J]. Acta Automatica Sinica, 2014, 40(9): 1875-1881. (in Chinese)
[11] Arablouei R, Doanay K. Modified quasi-OBE algorithm with improved numerical properties[J]. Signal Processing, 2013, 93(4): 797-803.
[12] Yu W, Joséde Jesús Rubio. Recurrent neural networks training with stable bounding ellipsoid algorithm[C]∥2007 American Control Conference. New York, 2007: 4768-4773.
[13] 何青, 王贤明. 基于集员估计理论的神经网络学习算法[J]. 中国水运, 2009, 12: 96-97.
He Qing, Wang Xianming. A neural network learning algorithm based on the theory of set membership estimation [J]. China Water Transport, 2009, 12: 96-97. (in Chinese)
[14] 姜燕, 何青. 集员估计理论在神经网络中的应用研究[J]. 电子测量与仪器学报, 2004(z2): 636-640.
Jiang Yan, He Qing. Application of set membership estimation theory to neural networks[J]. Journal of Electronic Measurement and Instrument, 2004(z2): 636-640. (in Chinese)
[15] Heddam S. Use of optimally pruned extreme learning machine(OP-ELM) in forecasting dissolved oxygen concentration(DO) several hours in advance: a case study from the Klamath river, oregon, USA[J]. Environmental Processes, 2016, 7(6): 1-29.
[16] 王焱, 汪震, 黄民翔. 基于OS-ELM 和Bootstrap 方法的超短期风电功率预测[J]. 电力系统自动化, 2014, 38(6): 14-19.
Wang Yan, Wang Zhen, Huang Minxiang. Ultra- short-term wind power prediction based on OS-ELM and bootstrap method[J]. Automation of electric power system, 2014, 38(6): 14-19. (in Chinese)
[17] Zhang H G, Yin Y X, Zhang S. An improved ELM algorithm for the measurement of hot metal temperature in blast furnace[J]. Neurocomputing, 2016, 22(1): 232-237.
SoftSensorforBallMillFillLevelBasedonOBE-ELMModel
CHENG Rui-hui, YAN Gao-wei
(College of Information Engineering, Taiyuan University of Technology, Taiyuan 030600, China)
In the process of soft sensor modeling of ball mill fill level using traditional extreme learning machine, existing the issue of poor robustness and low accuracy. To solve the problem, an improved extreme learning machine (ELM) soft sensor method based on optimal bounding ellipsoid (OBE) was proposed. The ball mill vibration signal was viewed as observed variables, and the features were extracted by partial least squares (PLS). Then, extracted features were put into ELM for model training. OBE was used to optimize the weights of the network under the condition that the model error was unknown but bounded. The experiment tested on a dataset of the lab-scale ball mill illustrate that the evaluation index is improved in the prediction of the ball mill fill level, and the box-plot shows that the proposed method has better robustness.
fill level of ball mill; soft sensor; optimal bounding ellipsoid; extreme learning machine
1673-3193(2017)05-0574-06
2017-04-19
国家自然科学基金资助项目(61450011); 山西省煤基重点科技攻关项目(MD2014-07); 山西省自然科学基金资助项目(20150110052)
程瑞辉(1992-), 男, 硕士, 主要从事人工神经网络及算法优化的研究.
TP29
A
10.3969/j.issn.1673-3193.2017.05.012
