基于CFD技术的管内流动精细仿真方法

孙致月， 陈 翾， 赵世明

(中国人民解放军91336部队， 河北 秦皇岛 066001)

基于CFD技术的管内流动精细仿真方法

孙致月， 陈 翾， 赵世明

(中国人民解放军91336部队， 河北 秦皇岛 066001)

利用数值仿真方法模拟管内流动具有适应性好、 高效方便的优势. 充分考虑到管道壁面对管内流动的作用， 引入湍流双层流动模型分别对近壁面和管道中心流场进行求解. 采用增强壁面处理方法描述壁面对流场参数的影响关系， 选取了合理的边界条件和计算区域以消除管道物理模型对流场边界的反作用， 基于CFD技术发展了一种可对管内流动进行精细模拟的数值方法. 通过对典型直管和三维细长管道的计算结果的分析， 表明所建立的数值方法准确模拟了管道入口处流场的发展过程， 通过对数值计算结果与理论计算结果的对比分析， 表明所建立的数值方法正确、 模拟精度较高.

管内流动； 数值仿真； CFD； 精细模拟

0 引 言

管内流动是一类重要的流动形态， 它广泛存在于机械、 能源、 化工、 航空航天、 船舶等实际工程应用中[1-5]. 管内流动的正向问题是充分了解已有管道的流动及压力损失状态， 为管道流动驱动等机构提供设计依据； 反向问题则是在已存外部条件下， 优化管道结构而获得期望的流动状态和压力损失.

研究管内流动的方法主要有理论分析、 实验方法和仿真方法. 理论方法基于流动遵循的一般规律求解流动状态， 由于求解方程复杂、 流动状态多样性致使获得方程解析解较为困难， 理论方法求解中往往需要做简化假设， 仅能求解简单形状管道如圆管、 充分发展流动、 粘性作用适中等特殊条件下的管内流动状态， 在求解管道能量损失时， 仅能在缓变流假设条件下计算管道沿程损失和简单形状的局部损失， 对于其它更多的复杂情况则无能为力. 实验方法虽能弥补理论方法的部分劣势， 却也存在管内流动参数测量困难、 无法测量管内全流场参数等不足， 同时还存在实验实施周期长、 成本高等显著缺点. 计算流体力学(CFD)技术将求解流动区域采用有限体积或有限元方法网格化处理， 并对流动控制方程在各网格上进行差分， 采用求解偏微分方程的数值方法求解各控制方程. 相比实验方法， 数值仿真方法可以获得全流场参数， 并具有理论方法所缺失的适应性强、 求解方便等优势， 已成为研究流场状态的重要方法， 获得了广泛的工程应用. 管内流动的特点是受管道的约束， 精细仿真的关键是充分考虑管道壁面对流动的影响. 文献[6]采用简化的代数应力模式代替雷诺应力模式对典型的管道内流动进行了计算和分析， 在一定程度上模拟了部分流动特性， 但在管道外壁附近计算精度不足. 文献[7-9]针对工程实际问题进行了管道内或类似模型流动的数值计算， 侧重于问题本身， 没有对管内流动数值方法进行专门研究和验证， 并认为管内流场数值模拟面临着严峻的挑战[7].

本文在详细研究不同管内流动形态和特点的基础上， 建立不同流动形态下管道流动的数学模型和仿真方法， 并验证仿真方法的准确性.

1 管内流动数学模型

1.1 基本控制方程

管内流动作为一种流动形态， 满足描述流场状态的一般控制方程， 考虑到数值求解的方便， 采用守恒型的雷诺平均N-S方程描述管内流动

式中： 下标i和j分别代表坐标方向；ρ为流动介质密度；u为速度；p为压力；μ+μt为等效粘性系数；μ为分子粘性系数；μt为Boussinesq湍流粘性系数.

1.2 湍流方程

为了闭合控制方程， 需要引入湍流模型计算μt. 湍流模型须与流场的特征密切相关， 管内流动受管道壁面的影响十分显著， 且流场一般具有细长非对称几何特征. 为充分地模拟管道壁面附近粘性起主导作用区域及湍流区域的流动特征， 一种易想见的方法是对管道近壁面区域A和其它区域B分别采用不同的湍流模型.

在区域A采用具有广泛适应性的k-ε湍流模型， 输运方程为

区域A湍流粘度μt,A的计算公式为

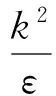
以上各式中，Gk是速度梯度引起的湍流动能，σk，σε是普朗特数，C1ε,C2ε,Cμ是常数.

区域B内也采用k-ε湍流模型， 并将ε输运方程修正为

区域B内湍流粘度μt,B的计算公式为

式中：lε,lμ均与湍流雷诺数Rey相关. 定义

式中：k为湍流动能；y为数值计算网格中心与壁面之间距离.Rey能反映计算网格与壁面的距离， 可作为区域A、B的区分参数， 即

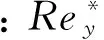
由以上湍流输运方程可分别获得区域A、B的湍流粘度， 但存在一个问题， 即两区域临界处湍流粘度不光滑， 这与实际情况不符. 为改进这一问题， 对区域A、B湍流粘度进行处理， 根据计算网格处的Rey值对μt,A和μt,B值进行加权平均， 得到

式中：λε是Rey的函数.

2 仿真模型建立

以典型三维细长管道为例描述管内流动仿真模型的建立方法. 管内流动仿真物理模型如图 1 所示.

图 1 管内流动仿真物理模型Fig.1 Schematic of pipe flow simulation’s model

物理模型由3段截面直径不同的直管和两个不同形状的弯角组成， 沿着直角坐标系z轴负方向， 将3段直管分别标示为Ⅰ, Ⅱ, Ⅲ， 直管Ⅰ和直管Ⅱ之间采用变直径的90°拐角连接， 直管Ⅱ和直管Ⅲ之间采用渐变直径的相切圆弧拐角连接. 各直管截面直径不同， 直管尺寸分别为： 直管Ⅰ截面直径为14 mm， 长度为372 mm； 直管Ⅱ截面直径为19 mm， 长度为450 mm； 直管Ⅲ截面直径为24 mm， 长度为600 mm.

当管道入口总压和出口压力确定并存在压差的情况下， 流体在管内产生流动， 本文仿真中取流体为20 ℃的水， 其物理性质见参考文献[10]. 求解计算域为管道出口、 入口边界和壁面所围成的内部流动空间. 在计算域内分布六面体网格， 为了提高计算精度减少网格数量， 在计算域流场参数变化剧烈的位置对网格进行适当加密， 整个计算域网格数量为1.11×106. 为了精确描述管道壁面对流动的影响， 采用增强壁面函数处理方法， 需要在流动粘性底层内(y+<5)分布足够数量的网格， 如图 2(b)～(d)所示分别为管道截面和两拐角位置处网格分布.

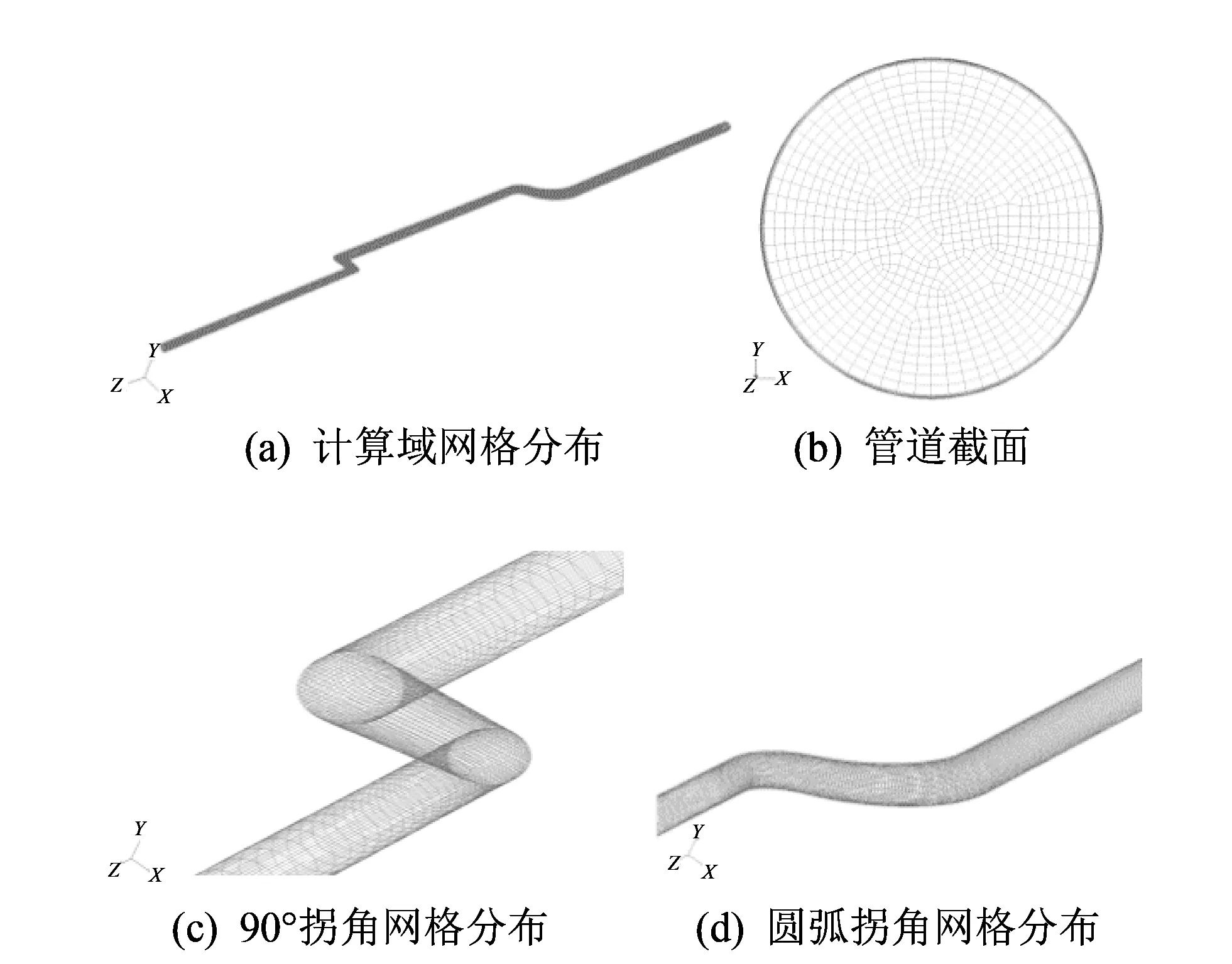
图 2 管内流动仿真网格划分Fig.2 Mesh of pipe flow simulation

设定管道左端为压力入口边界， 右端为压力出口边界， 管道壁面为无滑移壁面边界. 采用有限体积法， 在各网格点上用二阶迎风格式离散控制方程. 采用基于压力的隐式方法求解数值模型， 用SIMPLE方法耦合速度和压力. 为了提高计算精度及收敛速度， 用双精度储存及处理数据， 并采用了多重网格方法求解方程.

3 仿真方法验证

基于所建立仿真模型， 对上文所述管内流动进行计算. 管内流动边界条件见表 1.

表 1 管内流动仿真边界条件Tab.1 Boundary conditions of pipe flow simulation

3.1 管内流动的发展过程

流体流入管道后， 在管道壁面的影响下， 流场状态参数经历一个渐变发展的过程， 并最终达到充分发展状态， 此过程称为管内流动的发展过程. 为了使管内流动能达到充分发展流动状态， 采用直径d=20 mm， 总长度l=2 000 mm的细长直管进行计算. 如图 3 所示为管内流动达到充分发展状态后速度沿管道径向变化曲线.

图 3 中， 纵坐标为管道半径， 由中心指向壁面， 横坐标为无量纲速度， 表示速度与管道中心速度之比. 由图可见， 当管内流动充分发展后， 管内流动速度沿径向分布较为平坦， 这是典型的湍流流动速度分布特征. 经与管道径向速度幂次规律分布[10]对比， 可见仿真计算结果与理论计算结果吻合较好. 在此种情况下， 管道流动雷诺数Re=ρdv/μ=2×105， 远远大于管道流动中层流向湍流转捩的临界雷诺数2 300， 与图 3 所体现的速度分布特征相对应. 表明所建立的数值方法很好地模拟了管内流动参数径向分布特征.

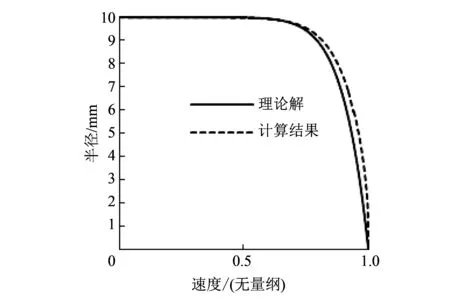
图 3 管道内流动充分发展的径向速度分布Fig.3 Velocity distribution of fully developed pipe flow in radial direction

3.2 管内流动壁面摩擦系数

对于直径不变的圆管， 由于管内各截面上速度相同， 则管道壁面摩擦力相同， 因此沿轴向管内流动静压呈线性关系降低. 如图 4 所示为仿真计算所得静压沿管道轴向变化的关系曲线， 所得结果与理论分析相符.

图 4 管内流动静压沿轴向分布图Fig.4 Static pressure distribution of pipe flow in axial direction

在不同工况下计算管道壁面摩擦系数f， 并与普朗特公式[11]计算结果进行对比. 对比结果如表 2 所示， 可见所建立的数值仿真方法能较精确地得到管道壁面摩擦系数.

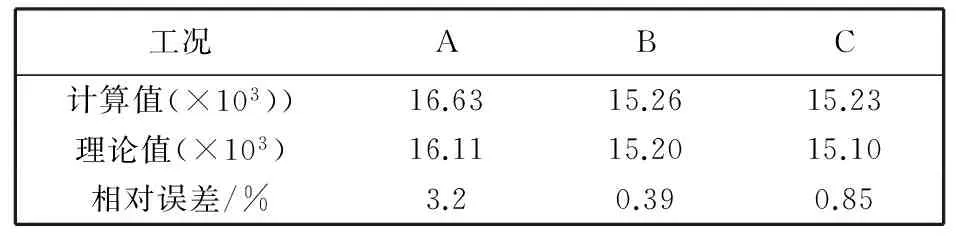
表 2 不同工况下壁面摩擦系数对比Tab.2 Comparison of wall friction coefficient in different work conditions

4 三维管内流动仿真

采用所建立的数值方法对前文所述三维管道内流动进行计算. 在管道不同位置处设置观测面以显示管道流动状态， 如图 5 所示， 由管道入口向后分别编号： 面1～面6， 其中面1为管道入口， 面6为管道出口. 面4位于直角坐标系XOY平面内， 面1， 2， 3位于Z轴正方向上， 面5， 6位于Z轴负方向上.

图 5 三维管道观测面设置示意图Fig.5 Schematic of watch surface set in 3-D pipe

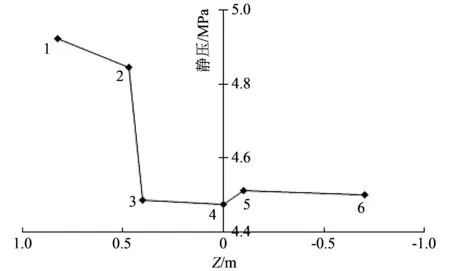
图 6 观测面上压力变化对比关系Fig.6 Comparison of static pressure on watch surfaces

图 6 所示为三维管道各观测面上压力变化对比关系图， 纵坐标为各观测面上静压均值， 横坐标为各观测面所在Z轴坐标. 由前述分析过程可知， 水流进入管道后， 经过充分发展过程后流动沿管道径向分布达到稳定. 三维管道直管Ⅰ、 Ⅱ、 Ⅲ处直径逐渐增大， 则其速度呈现逐渐降低的趋势. 由图 6 可见， 沿管内流体流动方向， 管道内压力总体呈下降趋势， 这是由于管道截面积变化不大的情况下， 管内压力损失主要反映为静压的降低. 面5处由于管道直径增大， 管内流速降低显著， 管道对流体产生扩压作用， 静压的增大抵消了水力损失作用， 压力总体表现为增大. 而面3处虽然管道直径增大， 但是由于直角拐弯产生巨大水力损失， 因此压力总体依然降低.

管道内水力损失主要包括沿程损失和局部损失， 流线曲折是引起管道内水力损失的重要因素. 如图7(a)所示为三维管道内流线图， 由图可见均匀缓变流经过第一个直角拐弯后流体质点相互掺混、 流线弯曲扭转， 伴随分离、 漩涡， 管内流场突变为急变流， 由于惯性作用甚至当流体重新进入直管内仍无法达到均匀.

图 7 三维管道流线图Fig.7 Streamlines in 3-D pipe

图7(b),(c)所示为直角拐弯处流线图. 由图7(b) 可见， 流体流过弯管时， 在弯管内侧形成分离区， 产生漩涡. 由于流体质点离心力的不平衡， 在弯管横截面上造成一个双漩涡形的二次流动， 如图7(c)， 与沿轴线的主流流动叠加后， 流体质点运动呈螺旋形状， 管道内流动更加复杂. 这也正是制约理论方法与实验方法精确预测管道流场、 准确计算其水力损失的重要原因.

相比而言， 由于流场的极度紊乱， 直角拐弯处局部能量损失系数较大， 直角拐弯在管道设计中应尽量加以避免. 如图 7(d)所示为直管Ⅱ和直管Ⅲ之间渐变直径的相切圆弧拐角处流线图， 可见虽然此处流线也有相互扭曲的现象， 较之直角拐弯处漩涡等极端混乱的运动现象并未出现， 可以预见其局部阻力损失系数较小.

图 8 所示为三维管道各观测面上总压变化对比关系曲线， 纵坐标为各观测面上总压均值， 横坐标为各观测面所在Z轴坐标. 观测面2和3之间总压降低量为直角拐弯处压力损失， 观测面4和5之间总压降低量为相切圆弧拐角处压力损失， 可见直角拐弯处局部损失远大于后者， 并在整个管道压力损失中贡献较大比例. 比较3段直管， 其压力损失为沿程损失， 斜率依次降低， 这是流动速度降低和管道摩擦力相应变化后的综合反映.

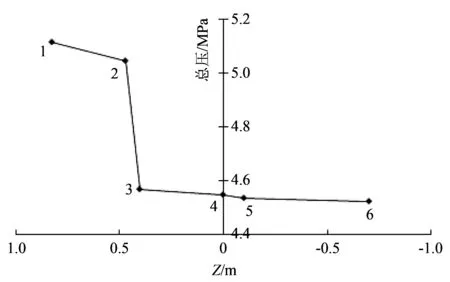
图 8 三维管道总压变化对比关系Fig.8 Comparison of total pressure on watch surfaces in 3-D pipe

5 结 论

在充分考虑管道壁面这一影响管内流动的主要因素的情况下， 应用特殊的湍流模型和增强的壁面处理方法模拟了壁面对管内流动的影响， 采用CFD技术建立了一种通用的管内流动仿真方法. 采用该方法对圆直管道流场进行求解， 并与特殊典型流态下的理论值进行了对比， 该方法精确模拟了充分发展流动的速度径向分布， 壁面摩擦系数仿真结果与理论值最大误差为5.1%； 该方法很好地模拟了三维管道内复杂流场分布， 尤其是直角拐弯和相切圆弧拐弯的流动特性和水力损失.

应用数值仿真方法可以获得复杂管道的全流场、 全参数的仿真结果， 本文所建立精细仿真方法能用于描述和预测复杂管道流场状态和管道水力损失的计算， 可用于对管道进行结构优化和辅助设计. 将本文所建立的数值方法应用于金属/水冲压发动机进水管道水动力预测， 经与自由航行试验测量值对比， 已印证该数值方法具有较高的精度.

[1] 邓冬. 回转弯道对竖直U型管内液氮流动与传热的影响研究[D]. 上海： 上海交通大学， 2014.

[2] 王广飞， 阎昌琪， 孙立成， 等. 窄矩形通道内两相流动压降特性研究[J]. 原子能科学技术， 2011， 45(6)： 677-681.

Wang Guangfei, Yan Changqi, Sun Licheng, et al. Investigation on resistance characteristics of two phase flow through narrow rectangular duct[J]. Atomic Energy Science and Technology, 2011,45(6)： 677-681. (in Chinese)

[3] 缪万波， 夏智勋， 罗振兵， 等. 金属/水反应冲压发动机进水管路的工作特性[J]. 固体火箭技术， 2007， 30(4)： 311-314.

Miao Wanbo, Xia Zhixun, Luo Zhenbing, et al. Work properties of inlet pipeline of metal/water reaction ramjet[J]. Journal of Solid Rocket Technology, 2007, 30(4)： 311-314. (in Chinese)

[4] 龚斌， 刘喜兴， 杨帅， 等. 90°圆形截面弯管内流动的大涡模拟[J]. 过程工程学报， 2013， 13(5)： 760-765.

Gong Bin, Liu Xixing, Yang Shuai, et al. Simulation on large eddy turbulent flow in a circular-section 90° bend[J]. The Chinese Journal of Process Engineering, 2013,13(5)： 760-765. (in Chinese)

[5] 徐强， 郭烈锦， 邹遂丰， 等. 管内蒸汽射流凝结压力波特性的小波分析[J]. 工程热物理学报， 2015， 36(7)： 1492-1495.

Xu Qiang, Guo Liejin, Zou Suifeng, et al. Investigation on pressure wave induced by steam jet condensation in water flow in a vertical pipe[J]. Journal of Engineering Thermophysics, 2015, 36(7)： 1492-1495. (in Chinese)

[6] 钱炜祺， 符松. 弯曲管道内湍流流动的数值模拟[J]. 推进技术， 2001, 22(2)： 129-132.

Qian Weiqi, Fu Song. Numerical simulation of turbulent flow in a turn-around duct[J]. Journal of Propulsion Technology, 2001, 22(2)： 129-132. (in Chinese)

[7] 蔡报炜， 王建军. 波浪管内流场与传热及阻力特性数值模拟[J]. 原子能科学技术， 2014， 48(7)： 1194-1199.

Cai Baowei, Wang Jianjun. Numerical study on flow field with heat transfer and flow resistance in wavy tube[J]. Atomic Energy Science and Technology, 2014,48(7)： 1194-1199. (in Chinese)

[8] 朱冬生， 郭新超， 刘庆亮. 扭曲管管内传热及流动特性数值模拟[J]. 流体机械， 2012,40(2)： 63-67.

Zhu Dongsheng, Guo Xinchao, Liu Qingliang. Heat transfer performance and flow resistance of twisted tubes in the tube side[J]. Fluid Machinery, 2012, 40(2)： 63-67. (in Chinese)

[9] 刘大明. 汽油机缸内气流瞬态运动及近壁面流动特性的实验与模拟研究[D]. 天津： 天津大学， 2014.

[10] 景思睿， 张鸣远. 流体力学[M]. 西安： 西安交通大学出版社， 2003.

[11] 章梓雄， 董曾南. 粘性流体力学[M]. 北京： 清华大学出版社， 1998.

AnAccurateSimulationMethodofPipeFlowBasedonCFD

SUN Zhi-yue, CHEN Xuan, ZHAO Shi-ming

(The Unit 91336 of PLA, Qinhuangdao 066001, China)

Computational fluid dynamics (CFD) is considered as a robust, efficient and convenient method to solve the internal flow field of pipe. In order to simulate the impacts of presence of pipe walls, the two-layer turbulent model was employed to define the near-wall region and fully-turbulent region's flow respectively. The enhanced wall treatment was used to calculate flow field in near-wall region. Proper boundary conditions and simulation region were selected to prevent pipe's structure affecting the boundary conditions reversely, also to achieve more accurate simulation solutions. Used these models, an accurate computational method of pipe flow was built based on CFD technique. The internal flow field of two kinds of typical pipes, straight pipe and 3D curving pipe, were solved to use the built computational method. The flow field is quantitatively described well, such as the developing process when the fluid just flows into pipe. Parts of results can be attained numerically as well as analytically were compared, and the validity and accuracy of the computational method are proved.

pipe flow; computational simulation; CFD; accurate simulation

1673-3193(2017)05-0599-06

2016-12-14

孙致月(1984-)， 男， 工程师， 硕士， 主要从事武器试验与仿真技术研究.

O368

A

10.3969/j.issn.1673-3193.2017.05.016