《数学分析》中不定积分求解方法探讨
2017-12-22
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
《数学分析》中不定积分求解方法探讨
吴红星,黄时祥,马江山,丁鹏,黄美春
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
不定积分的求解是《数学分析》中最基本、最重要的内容之一,它是定积分、重积分和曲线积分等后续内容的基础。研究了不定积分若干求解方法,详细探讨了凑微分积分法、拆微分积分法和分部积分法在求不定积分中的应用。
不定积分;定义积分法;凑微分积分法;拆微分积分法;分部积分法
不定积分是《数学分析》中的一个重要内容[1-2]。近年来,对不定积分的求解和教学方法研究有许多工作[3-14]。文献[3]给出了一类分部积分求解的简便算法;文献[4]给出了一类反函数的不定积分求解方法;文献[5]从教学方面讨论了不定积分的解题技巧;文献[6]探讨了|f(x)|不定积分的求解方法;文献[7]讨论了一类特殊三角函数有理式积分的求解方法;文献[8]讨论了一类有理幂函数的计算方法;文献[9]讨论了三角函数等三类特殊不定积分计算方法;文献[10]讨论了几种常见不定积分的计算方法与解题技巧;文献[11]通过给出口诀,讨论了不定积分的分部积分法;文献[12]采用凑微分法讨论了不定积分计算方法和解题技巧;文献[13]采用了第一类换元法等多种不同的方法讨论了不定积分,对大学生学习不定积分启发颇深;文献[14]讨论了不定积分求解的广义分部积分公式。本文系统地阐述了《数学分析》中不定积分求解的若干方法,为高校教师不定积分教学提供便利,对大学生学习不定积分具有启发意义。
1 定义积分法
设f(x)是定义在区间I上的函数,若成立F′(x)=f(x),x∈I,则称F(x)为f(x)的一个原函数,f(x)在区间I上的全体原函数记为f(x)在I上的不定积分,记作

(1)
方程(1)称为定义法积分公式,其中C为任意数。定义积分法指直接使用不定积分的概念与线性性质来求解不定积分,即熟记基本积分表[1]。
2 凑微分积分法
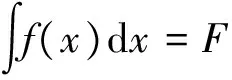
(2)
方程(2)称为凑微分法积分公式,凑微分积分法又称第一换元积分法。已知函数f(u)可积,
被积函数项可通过以下六种方法进行凑微分,以达到可积分的目的。


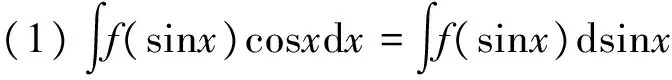
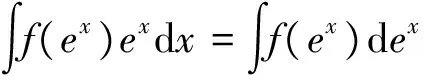

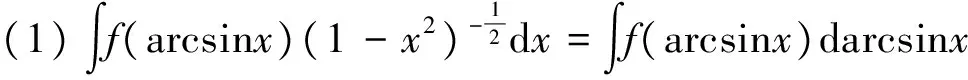

解:根据凑微分积分法可得:
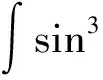

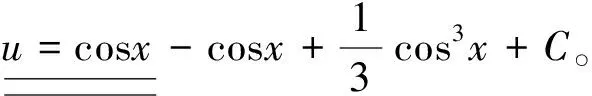
3 拆微分积分法
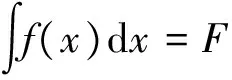
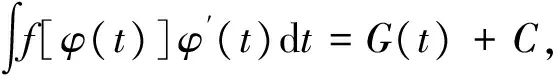
(3)
则

(4)
方程(4)称为拆微分法积分公式,拆微分积分法又称第二换元积分法。拆微分积分法常用代换方法主要包括:三角代换、无理代换、倒代换、万能代换、双曲代换和Euler代换,等等。
3.1 三角代换
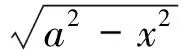
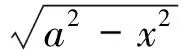
(5)
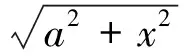
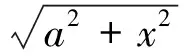
(6)

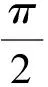


(7)
3.2 无理代换
x=tn, dx=ntn-1dt
(8)
于是原被积函数可化为关于t的有理函数。
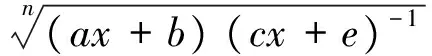
(9)
于是原被积函数可化为关于t的有理函数。
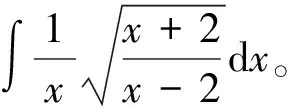

=ln1+t-ln1-t-2arctant+C
3.3 倒代换
当被积函数中分母次数高于分子次数,且分子分母均为“因式”时,通常可作倒代换:
x=t-1, dx=-t-2dt
(10)
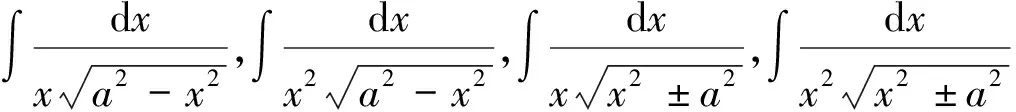

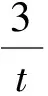
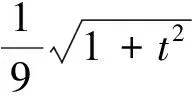

3.4 万能代换


(11)

(12)

(13)



于是得到:
3.5 双曲代换
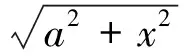
注1:化简时常用到双曲函数的一些恒等式有:


3.6 Euler代换
(1) 若a>0,则可令:

(14)
(2) 若c>0,则可令:

(15)
(3) 若二次三项式ax2+bx+c有相异实根λ,μ,即ax2+bx+c=a(x-λ)(x-μ),则可令:

(16)
注2:根据上式,所求的积分可化为关于t的有理函数的不定积分。



于是可得:

4 分部积分法
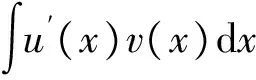

(17)

图1 分部积分法公式演示图
注3:图1中斜向乘积带“+”表示已经积出的函数,横向乘积带“-”表示新的被积函数。
下面介绍使用分部积分法求积分具备的一般原则。
(1) 幂指型
若被积函数是由幂函数与指数函数的乘积形式构成,通常将指数函数凑进微分项,再使用分部积分法可使幂函数的“幂”降次,通常每使用一次分部积分法可使幂函数降幂1次。

解:此积分的被积函数由幂函数与指数函数的乘积形式构成,于是

再次使用分部积分法可得
(2) 幂三型
若被积函数是由幂函数与三角函数的乘积形式构成,通常将三角函数凑进微分项,再使用分部积分法可使幂函数的“幂”降次,通常每使用一次分部积分法可使幂函数降幂1次。
(3) 幂对型
若被积函数是由幂函数与对数函数的乘积形式构成,通常将幂函数凑进微分项,再使用分部积分法可达到求解的目的。
(4) 幂反型
若被积函数是由幂函数与反三角函数的乘积形式构成,通常将幂函数凑进微分项,再使用分部积分法可达到求解的目的。
(5) 指三型(循环型)
若被积函数是由指数函数与三角函数的乘积形式构成,那么这是一种循环型不定积分,可将指数函数凑进微分项,使用分部积分法运算,再次将指数函数凑进微分项,再次使用分部积分法运算,即连续两次使用分部积分法可达到求解的目的[1]。同理将三角函数凑进微分项,重复上面的步骤也可达到求解的目的。
5 其它类型积分法
除了以上介绍了求不定积分的方法外,还有递推积分法、待定系数积分法和解方程组积分法,等等。递推积分法通常用于求被积函数型如sinnx,cosnx,tannx,secnx,cscnx等的不定积分。待定系数积分法一般用于解决有理函数的不定积分,将有理函数分解成几个最简分式之和,然后再逐一求解[1]。
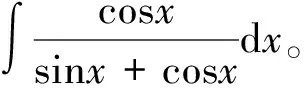
解:构造方程如下:
从而得到:
于是可得到:
其中C1,C2,C3,C4均为常数。
[1] 华东师范大学数学系.数学分析:上册[M].4版.北京:高等教育出版社,2010:178-179.
[2] 徐森林,薛春华.数学分析[M].北京:清华大学出版社,2005.
[3] 薛国民.关于一类分部积分的简便算法[J].工科数学,1995,11(1):264-266.
[4] 萧明达.关于含有反函数的一类不定积分[J].南京广播电视大学学报,1999,18(4):51-52.
[5] 廖新元.不定积分教法探讨[J].数学理论与应用,2001,21(4):127-128.
[6] 樊红云.|f(x)|不定积分的一种求法[J].高师理科学刊,2004,24(2):80-81.
[7] 展丙军,李兆兴.两类不定积分的巧解[J].高等数学研究,2005,8(6):20-24.
[8] 谢婉雯.一类有理幂函数不定积分的计算方法[J].大学数学,2006,22(1):111-113.
[9] 高丽,齐琼,谢瑞.关于三类特殊不定积分求解方法的讨论[J].西南民族大学学报(自然科学版),2010,36(2):169-171.
[10] 魏宏涛,康元宝.浅谈微积分教学中不定积分的计算方法与技巧[J].数学教学研究,2013,32(10):49-52.
[11] 胡结梅,郑华盛.不定积分计算方法注记[J].高等数学研究,2014,17(6):10-13.
[12] 杨恋波.对不定积分凑微分解法的再认识[J].哈尔滨师范大学自然科学学报,2015,31(1):31-32.
[13] 邢秀侠.一道不定积分题目的多种解法[J].教育教学论坛,2015(13):178-179.
[14] 冯晓慧,李菊娥.广义分部积分公式及其应用[J].高等数学研究,2016,19(6):22-23.
Discussion on the Methods for Solving Indefinite Integral in Mathematical Analysis
WU Hongxing,HUANG Shixiang,MA Jiangshan,DING Peng,HUANG Meichun
(School of Mathematics and Computer Science,Shangrao Normal University,Shangrao Jiangxi 334001,China)
The solution of indefinite integral is one of the most basic and important contents in mathematical analysis,it is the basis of the following contents such as definite integral,multiple integral and curvilinear integral. In this paper,we study some methods for solving indefinite integral,and we discuss the differential integral method,the split differential integral method and the partial integration method in detail.It provides reference for indefinite integral teaching,and has enlightening significance for studying indefinite integral.
indefinite integral;defined integration;the integral method of improvising differential;the integral method of differential disassembly;integration by parts
2017-08-31
江西省教学改革研究课题(JXJG-16-16-12);国家自然科学基金项目(11461055);江西省教育厅科技项目(151056)
吴红星(1980-),男,江西余干人,副教授,硕士,主要从事数学教学和迁移方程研究。E-mail:jxsruwhx@163.com
O172.2
A
1004-2237(2017)06-0005-07
10.3969/j.issn.1004-2237.2017.06.002
