渗流作用下深部巷道分区破坏的非欧模型
2017-12-22张铜宽潘一山钱七虎
张铜宽,潘一山,钱七虎
(1.辽宁工程技术大学 基础教学部,辽宁 葫芦岛 125000; 2.辽宁大学 物理学院,辽宁 沈阳 110000; 3.解放军理工大学 国防工程学院,江苏 南京 210007; 4.解放军理工大学 爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)
渗流作用下深部巷道分区破坏的非欧模型
张铜宽1,潘一山2,钱七虎3,4
(1.辽宁工程技术大学 基础教学部,辽宁 葫芦岛 125000; 2.辽宁大学 物理学院,辽宁 沈阳 110000; 3.解放军理工大学 国防工程学院,江苏 南京 210007; 4.解放军理工大学 爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)
深部开采过程中巷道围岩呈现分区破坏的特点。针对煤与瓦斯突出、底板破坏等实际工程问题获得了静水压力渗流作用下深部巷道的非欧模型应力分布解。新应力解由两部分组成:一部分是经典解,另一部分是非欧解。运用Mohr-Coulomb屈服准则作为判断新应力解分布引起分区裂化现象的条件。通过数值计算,获得了下列结论:当渗流压力存在时,深部围岩的分区破坏现象依然存在;远场渗透压力增加减小了靠近巷道的环向应力,且井壁渗透压力对巷道的环向应力的影响较小;在远场渗透压力作用下,孔隙度的增加降低了巷道的环向应力;运用Mohr-Coulomb屈服准则,估算了破坏区的位置和宽度;利用建立的有渗流作用的非欧模型解释了煤炭开采过程中的分区破坏现象。研究结果可为理解渗流作用下深部围岩分区破坏提供参考。
非欧模型;分区破坏;渗流作用;深部巷道
深部煤矿开采中,巷道围岩破坏区域和非破坏区域交替出现,这种现象称为分区破坏化现象(图1)。而根据经典弹塑性力学理论,浅部围岩由内向外依次出现破碎区、塑性区、弹性区(图2)。经典弹塑性力学难以解释分区破坏化现象。GUZEV M.A.和PAROSHIN A.A.等[1-7]认为岩石材料晶体中的点缺陷、线缺陷和面缺陷导致了连续性假设的失效,深部岩体内部已经不是经典的欧几里得空间,此时岩体内部的曲率张量(只考虑平面问题时)不再是0,协调性原理不再适用,内部空间不再是欧式空间,并且运用非欧几何和非平衡态热力学理论获得了深部岩体的非欧几何模型,解释了分区破坏化现象。钱七虎、周小平等[8-9]基于自由能密度、平衡方程和变形非协调性方程获得了新的非欧模型。钱七虎、戚承志等[9]通过引入有效塑性应变梯度获得了深部隧道分区破碎的内变量梯度塑性模型和岩体的内变量演化方程。但是,这些研究都没有考虑有水、瓦斯、油等的渗流作用。事实上,煤矿开采中,水、瓦斯的孔隙压力作用都不能忽略。截止2011年,我国煤与瓦斯突出矿井274处,高瓦斯矿井210处,瓦斯压力、孔隙压力一般可达到5 MPa。煤和瓦斯突出是在孔隙瓦斯压力作用下煤体变形问题。我国重点煤矿中具有底板突水危险性威胁的有285处。底板突出就是在孔隙水压力作用下底板的煤岩体破坏。在石油工程中,油、水在岩层中的渗流规律成为石油抽采的重要依据。在水、瓦斯、油等渗流作用下是否还存在分区碎裂化目前国内外还鲜有研究。而涉及到在渗流作用下的深部围岩的力学特征研究尚不多见。另一方面,潘一山、李忠华等[10-16]利用经典力学理论获得了渗流作用下围岩的应力分布规律。但是他们没有考虑非欧模型。本文主要结合了潘一山、李忠华和GUZEV等在渗流作用下围岩应力性质方面和非欧模型方面的研究成果,首次获得了在渗流作用下深部巷道的静水压力非欧模型。

图1 巷道围岩分区破坏示意Fig.1 Sketch map of zonal failure of roadway surrounding rock
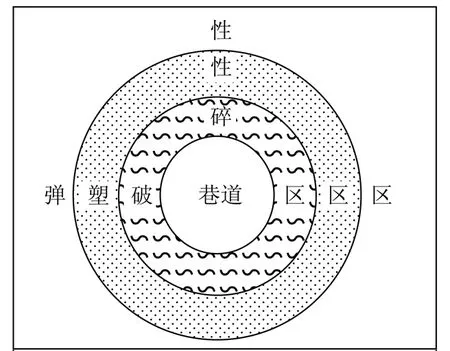
图2 巷道围岩经典破坏示意Fig.2 Sketch map of classical failure of roadway surrounding rock
1 非欧模型基本方程
欧式空间是指存在一个适用于全空间的笛卡尔坐标系,否则称为非欧氏空间。在力学中满足协调性方程的几何空间是欧氏空间,这意味着物体内部没有发生断裂或者嵌入;反之,当协调性方程没有满足时,物体内部发生了断裂或者嵌入。在数学上,区分欧式空间与非欧氏空间可以根据Riemann张量是否为零来判断:Riemann张量为零当且仅当欧氏空间成立;Riemann张量不为零当且仅当非欧氏空间成立。在平面应变问题中数量曲率为零当且仅当Riemann张量为零。
现在假设所研究问题为平面应变问题。在巷道截面中心建立直角坐标系,如图3所示。
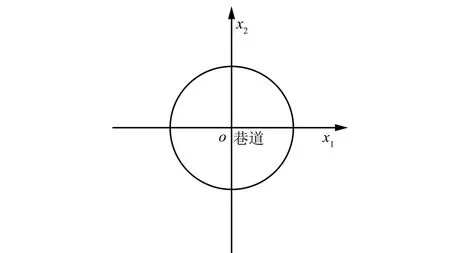
图3 巷道截面的直角坐标系示意Fig.3 Sketch map of rectangular coordinate for roadway section
位移场为u1,u2,应变ε11,ε12,ε21,ε22为
在弹性力学中,岩体为欧氏空间,满足协调性方程
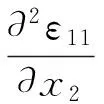
定义R为
其中,ε=ε11+ε22+ε33=ε11+ε22为坐标变换下的不变量。事实上,可以证明-R即为数量曲率。
设岩体未必满足欧式空间条件,Almansi张量由可逆应变εij和不可逆应变Pij组成,则
Aij=εij+pij
在运动中,
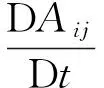
式中,D/Dt为全导数;vi为速度场。
令
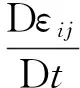
由于速度场是连续的,所以速度场满足协调性方程,故
Pll=P11+P22+P33
其中Δ为拉普拉斯算子。
不考虑时间效应,dR/dt=0,所以
设内能U为关于熵s、应变εij和R的函数U=U(s,εij,R)
其中,ρ0为巷道围岩密度;q为可由实验测得的适应参数;E为弹性模量;μ为泊松比。当R为0时,式(4)变为弹塑性力学的内能公式。
根据非平衡热动力学,热力学第一定律和第二定律可写为
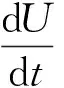
其中,ρ为巷道围岩密度;J(q)k为热流;J(s)k为熵流;D为耗散函数,D≥0。假设D具有双线性形式D=XiYj。
沿着运动轨迹,对内能U取关于时间的全导数,即Gibbs等式
成立,其中T为温度。
将式(6)代入式(5)得
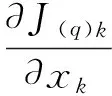
而
利用εij的对称性,有
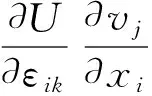
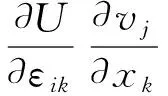
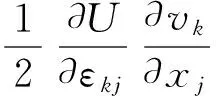
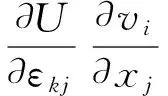
所以
其中,Pll=P11+P22+P33。
将式(9)改写为
再将式(8)和式(10)代入式(7),得
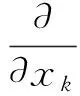
假设D具有双线性形式D=XiYi,则由式(11)可以得到
对于热流,有如下近似线性关系,其中λ为唯象参数
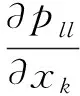
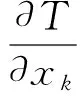
假设ρ=ρ0,将式(4)代入式(14)和式(15),可得
由热动力学,假设Pij与R有如下关系
其中ξ是一个唯象参数。且
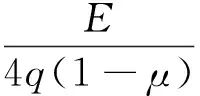
将式(18)代入式(2)可得
方程(19)的解为
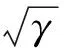
其中J0,N0,K0分别为0阶Bessel函数、Neumann函数、MacDonald函数;a,b,c为待定参数。
R(r)满足边界条件
R|r=r0=0,R′|r=r0=0
且R(r)满足
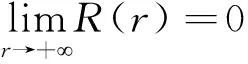
得到
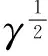
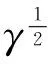
由本构方程
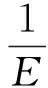
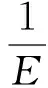
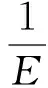

可得
σ33=μ(σ11+σ22)
令
σ=σ11+σ22+σ33
σ也是坐标变换下的不变量。则
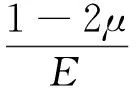
将本构关系代入式(1)得
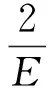
又在不考虑体力的情况下,根据平衡方程
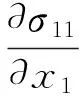
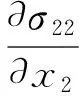
得
2 无渗流作用下巷道变形破坏的非欧模型应力解
假设巷道半径为r0,巷道所受地应力为σ0,且为静水压力。以巷道中心建立极坐标系,如图4所示。
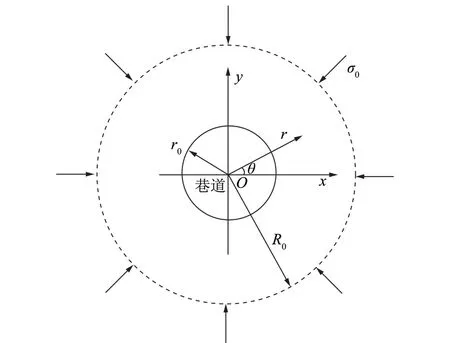
图4 巷道截面的极坐标系示意Fig.4 Sketch map of polar coordinate for roadway section
假设剪切应力σrθ=0,现将式(19)写为极坐标形式
其中
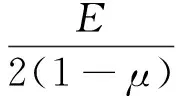
令
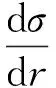
则式(22)变为
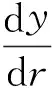
即
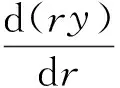
两边同时求积分得
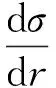
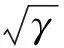
其中,J1,N1,K1分别为1阶Bessel函数、Neumann函数、MacDonald函数。
再对上式的左右两边同时求积分,得
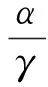
m1lnr+m2
其中,m1,m2为待定参数。因为当r充分大时σ近似为2(1+μ)σ0,故
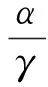
将式(23)代入平衡方程
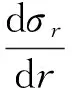
可得
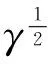
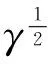
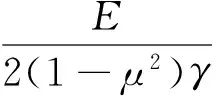
3 渗流作用下巷道变形破坏的非欧模型应力解
假设巷道半径为r0,地应力为σ0,且为静水压力。在距离巷道中心R0的圆周处分布有指向巷道圆心的大小均匀的远场渗流压p0,并且在巷道井壁周围均匀分布有指向井壁的井壁渗流压力p1。假设围岩均匀各向同性,且岩石为多孔介质。有效孔隙度为β,弹性模量为E,泊松比为μ,γ是给定的常数,可由实验测出。只考虑静水压力条件。围岩的受力情况如图5所示。
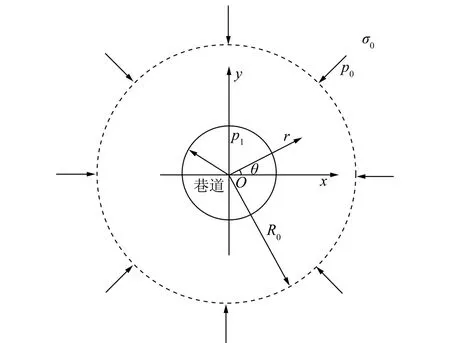
图5 渗流作用下巷道围岩应力示意Fig.5 Graph of the stress in the surrounding rock under the permeation
根据巷道的受力情况,边界条件为
σr|r=r0=(1-β)p1,σr|r=R0=σ0-βp0
含有渗流作用的巷道围岩平衡方程为
其中
将式(27)和公式σ=(1+μ)(σr+σθ)代入式(26)整理得
两边同时乘以r2得
等式两边同时求积分得
其中
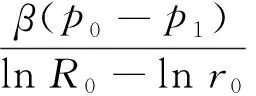
代入边界条件后,
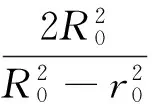
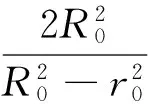


其中
所以,渗流作用下的巷道围岩的非欧几何模型应力场为
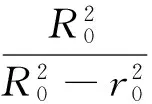

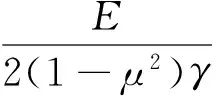
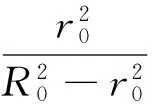
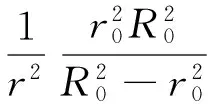
根据方程(26),经典弹塑性力学解为
其中
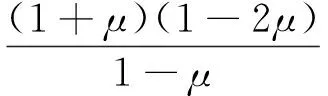
4 应力场影响分析
(1)在渗流作下,深部巷道依然存在分区破坏现象。
非欧模型获得的径向应力、环向应力与经典理论获得的径向应力、环向应力的图像如图6所示。
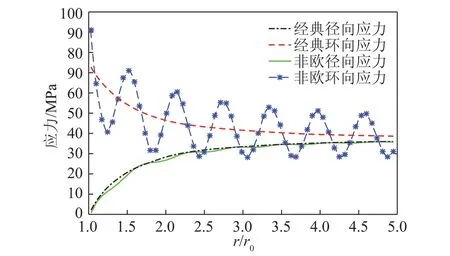
图6 经典理论与非欧模型的径向应力和环向应力Fig.6 Image of radial stress and angular stress in classical theory and non-Euclidean model
非欧模型条件下的径向应力围绕经典弹塑性力学意义下的径向应力小幅波动,且随着r逐渐增大,该波动逐渐减弱。非欧模型条件下的环向应力围绕经典弹塑性力学意义下的环向应力做幅度相当大的波动。根据此类性质,可以忽略径向应力的波动性而只专注于考虑环向应力。由于环向应力含有多个峰值,而在峰值处岩石可能发生失稳破坏进而导致多个破坏区,这样就形成了分区破坏现象。由于环向应力波动峰值较大,说明在渗流作用下的非欧模型中环向应力的波动峰值是造成围岩破坏的主要因素。
(2)随着围岩的渗透压逐渐增大,环向应力减小。
当远场渗流压力p0分别取0,5,10 MPa时,巷道的环向应力曲线如图7所示。
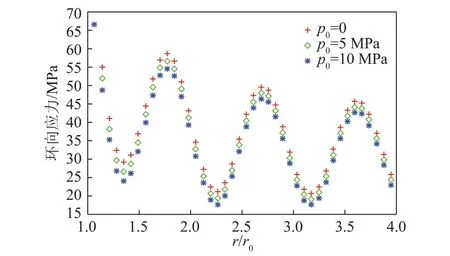
图7 不同的p0下的环向应力曲线Fig.7 Angular stress curvatures under the different p0
当井壁渗流压力p1分别取0,5,10 MPa时,巷道的环向应力曲线如图8所示。
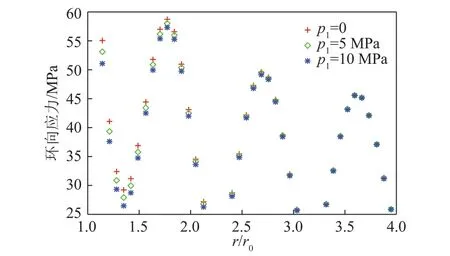
图8 不同的p1下的环向应力曲线Fig.8 Angular stress curvatures under the different p1
由图7可知,井壁渗流压力对环向应力的影响较小,所以只需分析当井壁渗流压力存在时孔隙度对环向应力的影响。这也说明在渗流作用下的非欧模型中,单纯改变井壁渗流压力是难以对围岩应力造成较大影响的。
(3)当地应力增加时,环向应力明显增加。
当地应力分别取32.5,40,47.5 MPa时不同的环向应力如图9所示。
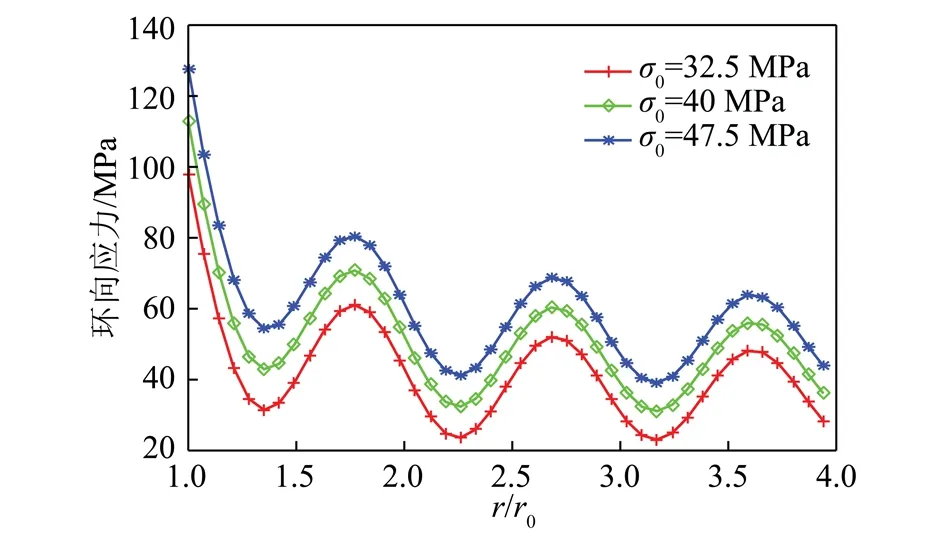
图9 不同地应力下的环向应力曲线Fig.9 Angular stress curvatures under the different crustal stresses
由图9可知,在有渗流作用的非欧模型中,地应力的增加,显著增加了环向应力波动峰值,进而对围岩的破坏起到很大的作用。
(4)在远场渗流压力存在时,有效孔隙度越大,环向应力越小。
在远场渗流压力为5 MPa时,且有效孔隙度β分别取0,0.15,0.3时,环向应力如图10所示。
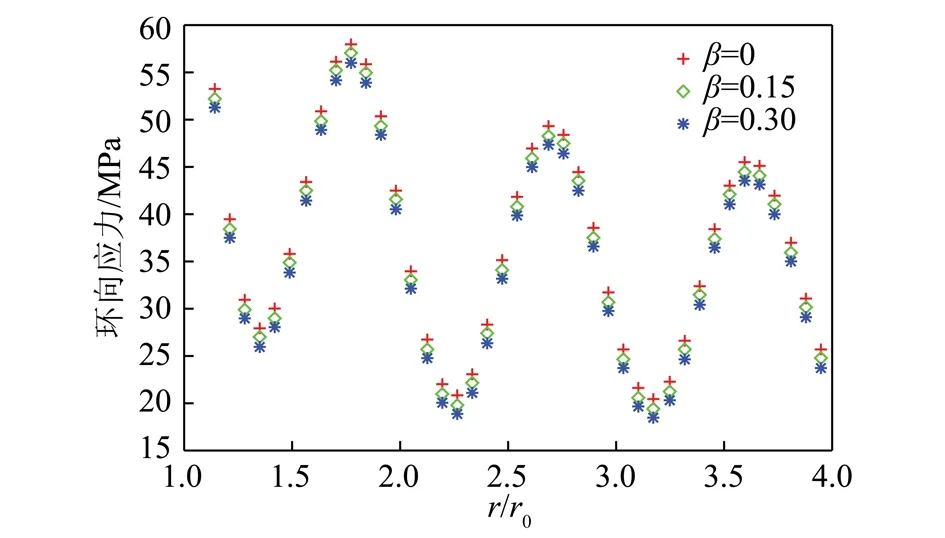
图10 当远场渗流压力存在时,不同β对应的环向应力曲线Fig.10 Angular stress curvatures with different β under the far field permeation pressure
(5)在弹性应力与塑性应力在数值上差别不是很大的情况下,利用Mohr-Coulomb屈服函数推断出非欧模型的破坏区的位置和宽度。
根据Mohr-Coulomb 准则,可得Mohr-Coulomb屈服函数:
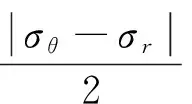
其中,φ为内摩擦角;f为Mohr-Coulomb屈服函数。假设屈服函数的临界值为c0(黏聚力),则当f>c0时,推测岩石可能出现破坏;当f 非欧模型的Mohr-Coulomb 屈服函数和黏聚力如图11所示。 图11 Mohr-Coulomb 屈服函数和黏聚力Fig.11 Image of Mohr-Coulomb yielding function and cohesion 由图1所示,破坏区是同心圆环。设破坏区Ⅰ、Ⅱ、Ⅲ中心到巷道的距离分别为l1,l2,l3(m),宽度分别为w1,w2,w3(m)。当巷道半径(m)取不同数值时相应的距离和宽度数值可见表1,2。 表1破坏区域与巷道中心之间的距离 巷道半径l1l2l3r0=2.02.223.916.24r0=2.22.434.106.43r0=2.42.654.296.63r0=2.62.884.486.83 表2破坏区域的宽度 巷道半径w1w2w3r0=2.00.441.060.80r0=2.20.471.080.76r0=2.40.511.100.73r0=2.60.561.150.71 冲击地压与瓦斯突出复合灾害,冲击地压与底板突水复合灾害都涉及瓦斯、水在煤体中渗流问题,利用上面的非欧模型应力解可以对这些灾害的发生进行解释和分析。 (1)在冲击地压预测中的作用 冲击地压是煤矿中重大动力灾害,危险性检测的一个实用方法是钻屑法。钻屑法是用42 mm的钻头向工作面煤壁中打孔,通过钻孔过程中排出的钻粉量来判断工作面煤体应力集中程度,进而来预测冲击地压的危险性。传统上随着向煤壁深度增加,应力逐渐增加,到达某一深度时应力达到最大值,再往深处钻孔应力又减小下来,应力峰值只有一个,反映在钻屑量上也是一样,钻屑量从煤壁向深处逐渐增大,达到峰值后逐渐下降。但是大量现场发现,钻屑量并不是服从这个规律,而是有几个峰值,以前都认为这种现象是由钻屑量的测量误差引起的。 例如:阜新王营矿采深达到了1 000 m以上。在4306工作面压力正常区域的煤层中打煤粉钻,钻头直径42 cm,孔深6~8 m,钻孔主要布置在两帮。为了确定钻屑量指标,钻孔每钻进一米测量一次钻屑量和粒度组成。记录每米煤粉量,然后画出钻屑量随钻孔深度曲线。图12是阜新王营矿4306下巷与胶带道叉口30 m处左右帮实测钻屑量变化曲线,图13是4306上巷距风门口160 m左右帮的实测钻屑量变化曲线,从图12和13可以看出,随钻深的增加,每米钻屑量变化趋势呈波浪变化趋势,这和以前浅部开采的钻屑量变化是不同的。 图12 阜新王家营矿4306下巷与胶带道叉口30 m处左右帮钻屑量曲线Fig.12 Drill cuttings weight curves of the folk between the 30 m away from belt road and the left part and right part of No.4306 lower roadway at Wangjiaying Mine at Fuxin 图13 阜新王家营矿4306上巷距风门160 m处左右帮钻屑量曲线Fig.13 Drill cuttings weight curves of the left part and right part of upper roadway where is 160 m away from the throttle at No.4306 at Wangjiaying Mine at Fuxin (2)在煤与瓦斯突出预测中的作用 钻屑量法也可有效地应用于地应力主导的煤与瓦斯突出的预测。在地应力主导的煤与瓦斯突出中,地应力煤与瓦斯突出的强度成正比。地应力的大小可以由钻屑量的多少来判断。钻屑量越多地应力越大,煤与瓦斯突出的程度越强。传统理论认为应力峰值只有一个,这样煤与瓦斯突出在钻孔深度上只有一个最可能发生位置。但是根据非欧模型,应力峰值会有多个,那么煤与瓦斯突出在钻孔深度上会有多个最可能发生位置。 例如:重庆天府矿业有限责任公司三汇一矿2124综采工作面的现场实验[17],该煤层采深为403~439 m,原始瓦斯压力3.6 MPa,工作面瓦斯压力1.8 MPa。这是典型的瓦斯渗流和煤层变形相互作用的案例。图14给出了钻屑量随钻孔深度的变化规律,可见钻屑量有波动性。以前多数现场认为是误差所致,实际上正是瓦斯渗流下的破裂分区化现象。某煤矿7607运输洞室的实验[18],该煤层采深约570 m,其钻屑量随着钻孔深度变化情况如图15所示。同样是瓦斯渗流下的破裂分区化现象。按照经典理论,巷道附近处应力会达到峰值。 图14 2124采煤工作面的钻屑量Fig.14 Graph of drill cuttings weight at 2124 coal mining face 图15 7607运输洞室的钻屑量Fig.15 Graph of drill cuttings weight at 7607 transport tunnel (1)在有渗流作用下非欧模型的深部巷道围岩应力场的解说明分区破坏现象依然存在。在渗流作用下非欧模型中,环向应力波动较大,是造成围岩破坏的主要因素。 (2)在有渗流作用下利用非欧几何模型获得的深部巷道围岩应力场的解中,远场渗流压力的增加降低了巷道的环向应力数值;而井壁渗流压力对环向应力影响较小。在渗流作用下非欧模型中,只增加井壁渗流压力难以显著影响围岩应力。 (3)在渗流作用下非欧模型中,地应力的增加对提升围岩的环向应力波动峰值最为显著,是围岩稳定性的主导因素。 (4)在不考虑远场渗流作用下,有效孔隙度增加减小了环向应力。说明在对围岩强度影响可以忽略不计的情况下,孔隙度的增加减小了环向应力,而非欧模型中环向应力是围岩破坏的主要因素,所以孔隙度的增加会在一定程度上增强围岩的稳定性。 (5)运用Mohr-Coulomb屈服准则,推算出破坏区的距离和宽度。估算出了巷道围岩应力集中的位置和范围。 (6)利用建立的有渗流作用的非欧模型,通过钻屑量随钻孔深度增加而波动这一工程现象,解释了煤炭开采过程中出现的分区破坏现象。 [1] GUZEV M A,PAROSHIN A A.Non-Euclidean model of the zonal disintegration of rocks around an underground working[J].Journal of Applied Mechanics and Technical Physics,2001,42(1):131-139. [2] GUZEV M A.Non-Euclidean models of elastoplastic materials with structure defects[M].LAP LAMBERT Mauritius Academic Publishing,2010. [3] GUZEV M A.Non-classical solution of a continuum model for rock descriptions[J].Journal of Rock Mechanics and Geotechnical Engineering,2014,6(3):180-185. [4] GUZEV M A.Usage of non-Euclidean model for description of rock[A].WSEAS International Conference on engineering mechanics,structures,engineering geology(EMESE’08)[C].2008. [5] GUZEV M A.The non-Euclidean model of zonal disintegration of rocks around an underground working[A].XXII International Congress of Theoretical and Applied Mechanics.Adelaide[C].Australia:University of Adelaide,2008:257. [6] GUZEV M A.Structure of kinematic and force fields in the Riemannian continuum model[J].Journal of Applied Mechanics and Technical Physics,2011,52(5):709-716. [7] KURLENYA M V,OPARIN V N.Scale factor of phenomena of zonal disintegration of rock and canonical series of atomic and ionic radii[J].Journal of Mining Science,1996,32(2):81-90. [8] 周小平,钱七虎.非协调变形下深部岩体破坏的非欧模型[J].岩石力学与工程学报,2013,32(4):767-774. ZHOU Xiaoping,QIAN Qihu.Non-Euclidean model of failure of deep rock masses under incompatible deformation[J].Chinese Journal of Rock Masses and Engineering,2013,32(4):767-774. [9] 周小平,周敏,钱七虎.深部岩体损伤对分区破裂化效应的影响[J].固体力学学报,2012,33(3):242-251. ZHOU Xiaoping,ZHOU Min,QIAN Qihu.Influence of rock damage on zonal disintegration around deep circular tunnels[J].Chinese Journal of Solid Mechanics,2012,33(3):242-251. [10] 戚承志,钱七虎,王明洋,等.深部隧道围岩分区破裂的内变量梯度塑性模型[J].岩石力学与工程学报,2012,31(S1):2722-2728. QI Chengzhi,QIAN Qihu,WANG Mingyang,et al.Internal variable gradient plasticity model for zonal disintegration of surrounding rocks in deep tunnels[J].Chinese Journal of Rock Masses and Engineering,2012,31(S1):2722-2728. [11] 李忠华,潘一山.有渗流作用的油井井壁稳定性的解析分析[J].工程力学,2002,19(3):105-108. LI Zhonghua,PAN Yishan.Stability analysis of wellbore with permeation[J].Engineering Mechanics,2002,19(3):105-108. [12] 潘一山,徐秉业.考虑损伤的圆形洞室岩爆分析[J].岩石力学与工程学报,1999,18(2):152-156. PAN Yishan,XU Bingye.The rock burst analysis of circular chamber under consideration of rock damage[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(2):152-156. [13] PAN Yishan,ZHANG Mengtao,LI Guozhen.The analysis of rock burst in coal mine[J].Journal of Coal Science & Engineering(China),1996,2(1):32-38. [14] 潘一山,罗浩,肖晓春,等.三轴条件下含瓦斯煤力电动感应规律的试验研究[J].煤炭学报,2012,37(6):918-922. PAN Yishan,LUO Hao,XIAO Xiaochun,et al.Experimental study on mechanical-charge induction law of coal containing gas under triaxial compression[J].Journal of China Coal Society,2012,37(6):918-922. [15] 潘一山,罗浩,李忠华,等.含瓦斯煤岩围压卸荷瓦斯渗流及电荷感应试验研究[J].岩石力学与工程学报 2015,34(4):1-7. PAN Yishan,LUO Hao,LI Zhonghua,et al.Experimental study of gas permeability and charge induction under confining pressure unloading progress of containing-gas coal rock[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(4):1-7. [16] 胡国忠,王宏图,范晓刚,等.低渗透突出煤的瓦斯渗流规律研究[J].岩石力学与工程学报,2009,28(12):2527-2534. HU Guozhong,WANG Hongtu,FAN Xiaogang,et al.Investigation on law of methane gas flow in coal with coal-gas outburst hazard and low permeability[J].Chinese Journal of Rock Masses and Engineering,2009,28(12):2527-2534. [17] 尹光志,李晓泉,赵洪宝,等.钻屑量与矿山压力及瓦斯压力关系现场实验研究[J].北京科技大学学报,2010,32(1):1-7. YIN Guangzhi,LI Xiaoquan,ZHAO Hongbao,et al.In-situ experimental study on the relation of drilling cuttings weight to ground pressure and gas pressure[J].Journal of University of Science and Technology Beijing,2010,32(1):1-7. [18] 曲方,张龙,李迎业,等.钻屑指标变化规律及其在突出预测中的应用[J].中国煤炭,2011,37(10):82-88. QU Fang,ZHANG Long,LI Yingye,et al.Variation of desorption index for drill cuttings and its application in predicting risk of coal and gas outburst[J].China Coal,2011,37(10):82-88. Non-Euclideanmodelforzonalfailureofdeeproadwayunderthepermeationaction ZHANG Tongkuan1,PAN Yishan2,QIAN Qihu3,4 (1.DepartmentofBasicTeaching,LiaoningTechnicalUniversity,Huludao125000,China; 2.DepartmentofPhysics,LiaoningUniversityShenyang110000,China; 3.EngineeringInstituteofNationalDefenseEngineering,PLAUniversityofScienceandTechnology,Nanjing210007,China; 4.StateKeyLaboratoryofDisasterPreventionandMitigationofExplosionandImpact,PLAUniversityofScienceandTechnology,Nanjing210007,China) In the process of deep mining,roadway surrounding rock presents zonal failure characteristic.The hydro-static non-Euclidean stress distribution solution of deep roadway under permeation action is obtained aiming at coal and gas outburst,floor failure and other practical engineering problems.The new stress solution consists of two parts:one is the classical solution;the other one is the non-Euclidean solution.The Mohr-Coulomb yielding criterion is applied for the condition that the new stress distribution causes zonal failure phenomenon.Through the numerical calculation,the following conclusions are obtained:When there is the permeation action,the zonal failure phenomenon still exists for deep surrounding rock;far field permeation pressure reduces the angular stress of roadway,and borehole permeation pressure influences the angular stress very small;under the far field permeation pressure,the increase of porosity reduces the angular stress of roadway;using the Mohr-Coulomb yield criterion,the location and width of the failure zones are estimated;by using the non-Euclidean model under the permeation,the zonal destruction in the process of coal mining is explained.The present study offers a reference to understanding the zonal failure in deep surrounding rock under the permeation action. non-Euclidean model;zonal failure;permeation action;deep roadway 张铜宽,潘一山,钱七虎.渗流作用下深部巷道分区破坏的非欧模型[J].煤炭学报,2017,42(11):2842-2851. 10.13225/j.cnki.jccs.2017.0454 ZHANG Tongkuan,PAN Yishan,QIAN Qihu.Non-Euclidean model for zonal failure of deep roadway under the permeation action[J].Journal of China Coal Society,2017,42(11):2842-2851.doi:10.13225/j.cnki.jccs.2017.0454 TD32 A 0253-9993(2017)11-2842-10 2017-04-08 2017-06-22责任编辑毕永华 国家重点研发计划资助项目(2017YFC0804208,2017YFC0804205,2016YFC0801403-4) 张铜宽(1982—),男,辽宁鞍山人,博士研究生。Tel:0429-5310096,E-mail:fsj1982@163.com。 潘一山(1964—),男,辽宁丹东人,博士生导师。E-mail:panyish_cn@sina.com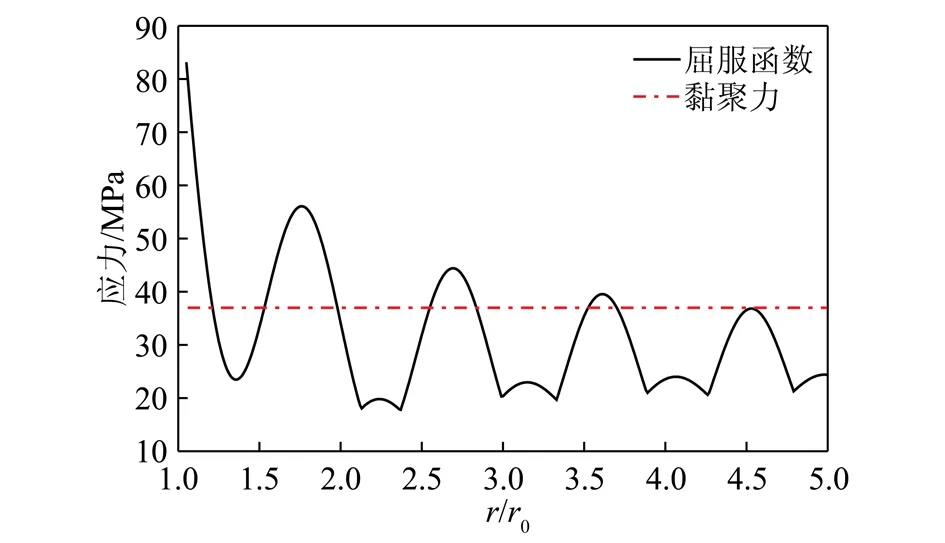
Table1Distancebetweenthefailurezonesandtheroadwaycenterm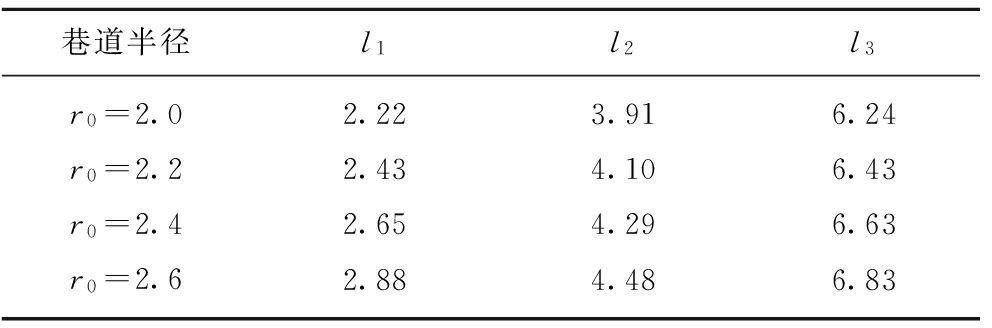
Table2Widthofthefailurezonesm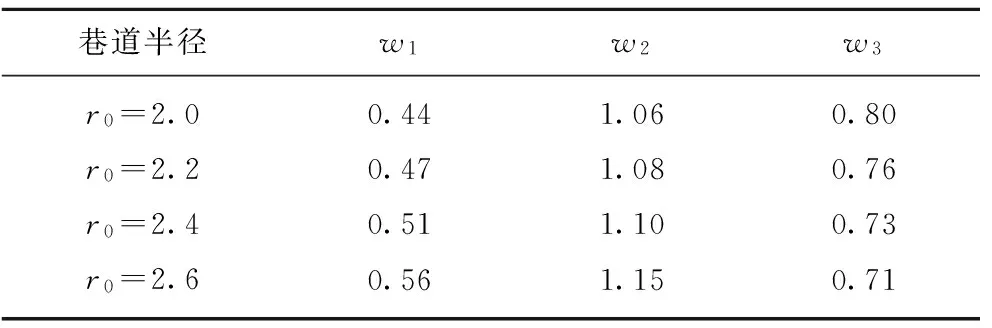
5 非欧模型的应用
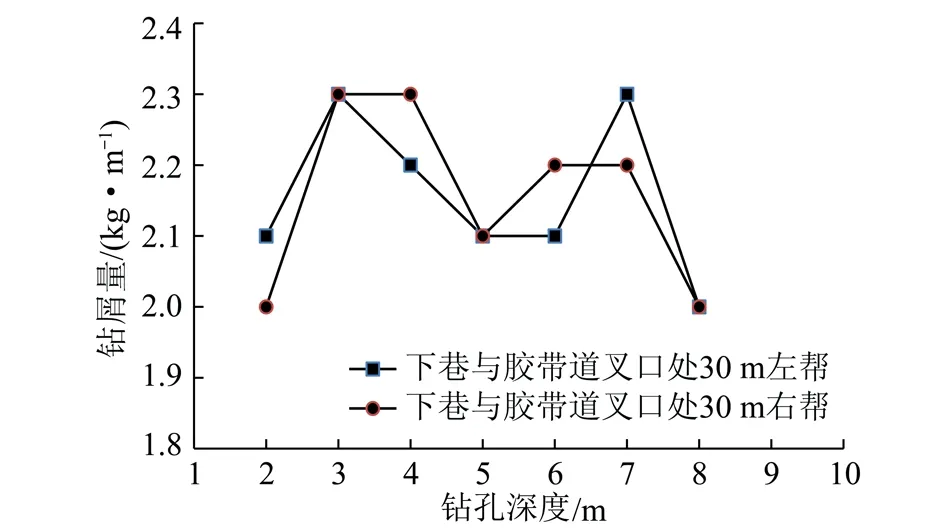
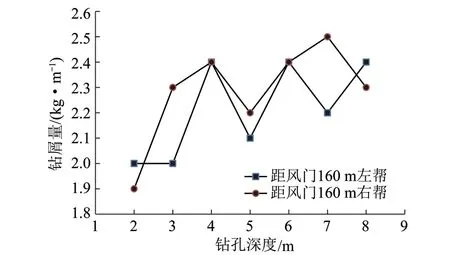
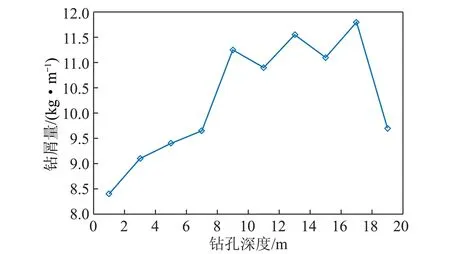

6 结 论
