改进K中心点算法在入侵检测的应用
2017-12-21魏明军
魏明军,田 昆
(华北理工大学,河北 唐山 063000)
改进K中心点算法在入侵检测的应用
魏明军,田 昆
(华北理工大学,河北 唐山 063000)
传统K中心点算法虽然改进了K均值算法对噪声和孤立点数据敏感的不足,但是仍存在着初始聚类中心和聚类个数k难以确定的问题,因此,针对算法存在的问题,提出一种基于密度的改进K中心点算法。该算法会根据数据集数据的分布情况自主确定聚类个数k和k个聚类中心点。最后,通过在入侵检测领域KDD Cup99数据集上实验测试表明,改进K中心点算法不仅能够自动形成k个聚类,而且具有较高的入侵检测率和较低的漏报率,聚类和入侵检测的效果均优于传统的K中心点算法。
入侵检测;K中心点算法;改进K中心点算法;聚类分析
入侵检测作为一种有别于防火墙的安全技术,能够提供对来自外部和内部攻击的实时监控。然而,传统的两种入侵检测技术误用检测和异常检测,在入侵检测性能的两个评价指标误检率和检测率上各有长短,前者的特点是误检率低但检测率低,不能检测新型的未知攻击,后者正好相反,特点是检测率高但误检率高,它能够检测出新型的攻击,适应性好,但是存在高误检率问题。
聚类分析是数据挖掘中常用的一种无监督的学习方法,它依据数据内部的潜在关联将数据集中的数据依据相似性划分成不同的分类,同一分类中的数据之间具有较高的相似度,不同分类的数据之间有较大的差异性,这一点正满足了入侵检测中异常检测的需要。异常检测需要建立正常行为库和异常行为库来区分正常行为和攻击行为,而且要求两个行为库各自内部的数据越相似越好,两个行为库之间数据差异性越大越好。因此,可以将聚类分析应用于入侵检测来提高入侵检测的检测率和降低漏报率。
1.K中心点算法
1.1 基本思想
K中心点算法与K均值算法是数据挖掘聚类分析中基于划分的算法中比较经典的两个算法,应用较为广泛。基于划分的聚类方法的思想是首先创建一个数据集的初始划分,然后采用迭代重定位技术,使样本在划分块间移动,提高聚类的相似度,最终得到一个较为完善的数据划分。K均值算法简单易实现,但是对噪声和孤立点数据敏感;K中心点算法改进了K均值算法的不足,具有较高的稳定性。
K中心点算法的基本思想:首先为每个分类随机选择一个中心点,然后计算剩余的数据对象与各分类中心之间的距离,根据距离的远近将数据对象分配给最近的一个分类;然后,计算每个簇中所有点的平均值,选用离平均值最近的点作为新的簇中心,再次对数据点进行划分,该过程不断循环直到类簇的中心不再发生变化(类簇的绝对误差之和收敛)为止。类簇的绝对误差之和直接反应了聚类的质量,它的值越小,表示类簇越紧凑,那么聚类效果就越好。
1.2 聚类步骤
输入:包含n个样本的数据集和簇数目k。
输出:k个类簇。
流程:
1) 随机选择k个样本点作为初始的簇中心;
2) 重复下列(1)(2)(3)(4)步骤直到k个中心点不再发生变化:
(1) 指派每个剩余样本给离它最近的中心点所代表的簇;
(2) 计算每个簇中所有点的均值作为候选簇中心点c;
(3) 随机地选择一个非中心点x;
(4) 如果用x代替候选中心点c后得到的聚类绝对误差和减小,则用x代替c形成新的中心点;
3) 输出k个类簇。
1.3 算法不足
K中心点聚类算法的优点是算法思想较简单,容易实现,同时能够有效降低噪声和孤立点的影响,但是该算法仍存在一些不足之处:
1)K中心点算法在聚类之初就需要输入聚类数目k,这样要想达到一个好的聚类效果往往要尝试很多次才可能找到一个比较合适的k值,所以存在着聚类数据k难以确定的问题。
2)K中心点算法存在因初始点的选取问题而导致不稳定的聚类结果的缺陷,容易使算法陷入局部最优解,不同的初始点不仅会导致不同的运行效率,更可能会产生不同的聚类结果,直接影响算法的实际应用效率。
2.改进K中心点算法
2.1 基本思想
改进K中心点算法的基本思想:聚类簇的中心点应该是邻域范围内密度最高且邻域平均距离最短的点,而且趋向于更高密度、更短平均距离的样本点移动。具体做法:采用定宽的聚类方法,预先设定聚类半径R,同时将数据点周围邻域半径R范围内包含的其他数据点的个数定义为该数据点的密度,将R范围内包含的其他数据点到该数据点的平均距离定义为该点的邻域平均距离,在聚类过程中调整各个类簇的聚类中心时,用各类簇中密度最高、邻域平均距离最短的数据点作为新的聚类中心,再次对数据点进行划分,直到各类簇中心不再发生变化时聚类终止。
2.2 相关概念
定义1 任意两个数据对象之间的欧几里得距离定义为:
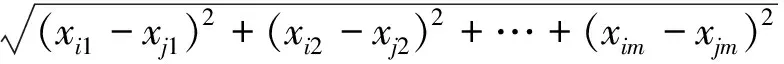
(1)
式中:xi=(xi1,xi2,…,xim),yj=(yj1,yj2,…,yjm)都是m维的数据对象。
定义2 训练数据集平均距离定义为:
(2)
定义3 数据对象的邻域半径R定义为:
(3)
式中:m为正整数,通常取值为2。
定义4 数据对象密度函数定义为:
Density(xi)={p|d(p,xi)πR,p∈X,xi∈X}
(4)
式中:X是数据对象集合,d(p,xi)为数据对象p到数据对象xi的距离,R代表邻域半径,采用欧几里得距离计算。
定义5R邻域平均距离定义为:
(5)
式中:NR是数据对象xi邻域半径R内的点数即Density(xi)。
数据集中的每个对象可以根据以上5个定义的计算方法计算出对应的数据对象的密度值及邻域平均距离,这两个值将会被用作聚类中选择聚类中心对象的依据。
2.3 算法描述
改进K中心点算法的整个算法描述如下:
输入:X={x1,x2,…,xn}是包含n个对象的数据集合,邻域半径R,阈值θ。
输出:k个数据分类。
过程:
1) 根据输入的数据对象,计算出R、每个对象的数据对象密度及邻域平均距离;
2) 将第一个数据对象x1作为类簇C1的中心点oc1:
Do
(1) 计算数据对象xi到每个聚类Cj聚类中心的距离d(xi,oj);
(2) 比较d(xi,oj)与邻域半径R大小,若d(xi,oj)≤R,比较数据对象xi与聚类中心点oj的数据对象密度和邻域平均距离,如果Density(xi)
Until所有类簇的聚类中心不再发生变化。
3.测试实验
3.1 实验数据集选择
KDDCup99 数据集是入侵检测领域比较权威的测试数据,测试用的数据选自数据集中的10%数据集“kddcup.data_10.percent”,该数据集共有494021个记录,正常网络数据的数目为97278,剩下全部为攻击行为数据。其中,攻击行为数据可以分为四个类别,分别是Dos攻击、U2R攻击、R2L攻击和Probe攻击。
聚类分析算法能够应用在入侵检测中是基于以下两个基本的假设:
(1)正常数据的数量远远大于攻击数据的数量;
(2)攻击数据在某些属性的取值上明显偏离正常的取值范围。
因此,在该数据集中选择2000条数据作为测试数据集,其中正常数据1960,异常数据40条,异常数据占比为2%,满足以上两个假设。
3.2 评价指标
对于入侵检测系统,评价其性能的最重要的两个指标是检测率和漏报率,二者的具体定义如下:
误报率=被误判为入侵的正常记录数/总测试记录中的正常记录数。
检测率=检测出来的入侵记录数/总测试中的入侵记录数。
3.3 性能实验
将数据集分别在K中心点算法和改进的K中心点算法上进行实验,最后比较算法性能。由于K中心点算法需要在聚类之初便确定聚类个数,而且聚类个数的不同选择将会对聚类算法的最终结果产生非常大的影响,因此在设置不同聚类个数的条件下得出的K中心点算法聚类效果如表1所示。
改进K中心点算法不需要在聚类之初便确定聚类的数目,它可以根据数据集中数据的特征自主确定产生聚类的数目。改进K中心点算法性能如表2。
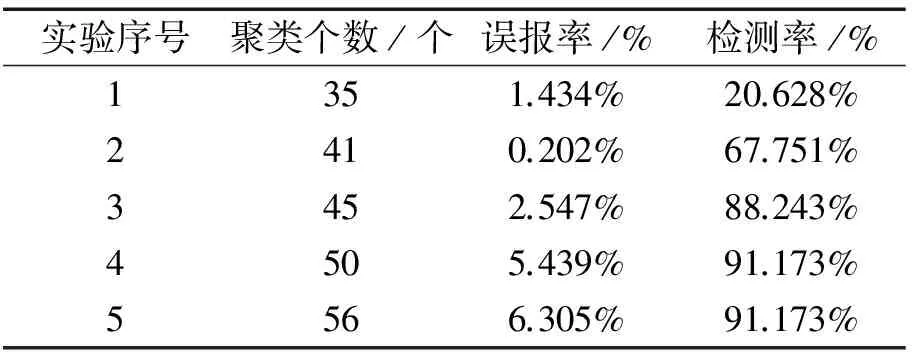
表1 K中心点算法性能

表2 改进K中心点算法性能
从表1和表2可以看出,和K中心点算法比较,改进K中心点算法在不需要输入聚类个数的前提下,能够根据数据特点找出比较适当的聚类数量,且有一个较好的误报率和检测率。
4. 结论
本文提出了基于密度的改进K中心点算法,解决了传统K中心点算法初始聚类中心和聚类个数k难以确定的问题。由实验结果可知,将改进算法应用在入侵检测的异常检测中,改进算法的聚类性能和入侵检测的检测性能均优于传统K中心点算法,因此将改进K中心点算法应用在入侵检测中可以提高入侵检测率,同时降低漏报率,有效提高入侵检测的性能。
[1]MohammadrezaEktefa,SaraMemar,FatimahSidi,LillySurianiAffendeyIntrusiondetectionusingdataminingtechniques[C]//In:Internationalconferenceoninformationretrievalandknowledgemanagement, 2010,200-204.
[2]苏家洪.入侵检测系统新技术介绍[J].中国新技术新产品,2012,0(3) :43-43.
[3]刘向旗. 基于数据挖掘的入侵检测系统研究[J]. 信息系统工程,2013,0(4):44-45.
[4]李贺玲. 数据挖掘在网络入侵检测中的应用研究[D]. 吉林:吉林大学,2013.
ApplicationofImprovedK-MedoidsAlgorithminIntrusionDetection
WEI Ming-jun, TIAN Kun
(North China University of Science and Technology, Tangshan 063000, China)
The k-means algorithm has the problem which is sensitive to noise and outlier data. Though the traditional k-medoids algorithm overcomes the problem, it still has another two problems. One is determining the initial cluster centers, and the other is determining the cluster number k. In order to solve the problems, an improved k-medoids algorithm based on density is proposed. It can determine the cluster number k and cluster centers independently according to the distribution of the data set. Experimental test on the KDD Cup99 data set in the intrusion detection field shows that the improved k-medoids can not only automatically form the center of the k cluster, but also has high detection rate and low false negative rate. The effect of clustering and intrusion detection is better than that of the traditional k-medoids algorithm.
intrusion detection; k-medoids algorithm; improved k-medoids algorithm; cluster analysis
TP393
A
1671-3974(2017)04-0057-03
2017-09-02
魏明军(1969- ),男,硕士,华北理工大学信息工程学院教授,研究方向:入侵检测,数据挖掘。
