一种计及雷电入射角的改进电气几何模型

龚 磊，郭 恒

（重庆电力设计院，重庆401121）

一种计及雷电入射角的改进电气几何模型

龚 磊，郭 恒

（重庆电力设计院，重庆401121）

以暴露距离作为计算手段的电气几何模型存在雷电入射方向固定以及难以适用于输电线路小保护角等缺点。为此，改进雷电入射方式，将雷电入射方向扩大至[-p/2，p/2]，并推导出不同雷电入射角下的暴露距离计算方法。以输电线路小保护角为例，传统方法与改进方法计算得到的绕击跳闸率分别为0.021 7、0.088 1次/(100 km·a)，对造成差异的原因从雷电入射概率和暴露距离两方面进行分析。分析表明，改进方法雷电入射概率为57.33%，小于传统模型；但其暴露距离在5.0 m左右波动，大于传统模型的1.35 m。此外，计算了两类模型在不同保护角下的绕击跳闸率，并根据计算结果对改进方法的有效性进行了验证。改进后的电气几何模型可克服传统方法不适用于小保护角或负保护角的缺点。

输电线路；雷电绕击；电气几何模型；雷电入射

0 引言

一直以来，雷击是引起输电线路跳闸的主要原因之一[1-6]。数据表明，雷电绕击引起的跳闸比率随输电线路运行电压的升高而增大[7-8]，而高电压等级输电线路的跳闸会给电网的安全稳定运行造成严重威胁。因此进行输电线路雷电绕击研究具有现实意义。

绕击跳闸率可以直观地反映出输电线路绕击耐雷性能，因此选择合适的计算方法尤其重要。目前常见的绕击跳闸率计算方法主要有规程法[9]、电气几何模型法[10-11]以及先导发展法[12-14]。电气几何模型将雷电活动参数与线路结构尺寸有机联系起来，物理意义明确且计算简便，因而获得了广泛应用。

然而，电气几何模型在计算暴露距离的过程中，雷电入射方向被固定为垂直向下，这与实际情况存在一定出入[15-18]。文献[16-18]进行了改进，提出将雷电入射角扩大至[0，p/2]，这较传统方法有了很大进步，但受地线屏蔽弧影响，暴露距离在[-p/2，0]和[0，p/2]下的计算方法并不相同，因此仅将雷电入射角限定在[0，p/2]内是不够的。本文将雷电入射角的变化范围进一步扩大至[-p/2，p/2]，并推导了雷电入射角在该范围内的暴露距离计算公式，从而获得了考虑雷电入射角的电气几何模型计算方法。

1 计及雷电入射角的电气几何模型

1.1 暴露弧与雷电入射角的关系

随着对线路防雷的认识及重视，输电线路设计趋向于小保护角甚至负保护角[19-20]。故笔者以小保护角为例对不同雷电入射角下的暴露距离计算方法进行说明。如图1所示，A代表地线，B代表导线；M为地线屏蔽弧与导线暴露弧的交点，N为导线暴露弧与大地捕雷面的交点，直线k1为过点N的切线，其与垂直方向的夹角为θ1，直线k2为过点M的切线，其与垂直方向的夹角为θ2，直线k3为弧与弧的公切线，其与垂直方向的夹角为θ3；设雷电入射角为y；K为雷电流与导线暴露弧的交点；β为表示导线与地线位置关系的夹角，为已知值。规定角θ1、θ2、θ3、ψ逆时针方向为“+”，顺时针方向为“-”。

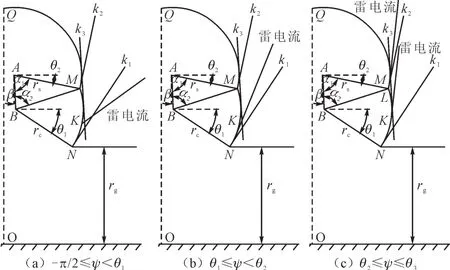
图1 考虑雷电入射角的电气几何模型Fig.1 EGM considering lightning strike angles

当雷电入射角y在不同区段变化时，暴露弧的计算方式如下：

1）当-p/2≤y＜q1时，如图1（a）所示，线路暴露弧为弧，暴露距离采用暴露弧在垂直雷电入射方向上的投影。

2）当q1≤ψ＜q2时，如图1（b）所示，线路暴露弧为弧，弧被线路自身暴露弧所屏蔽。

3）当q2≤ψ≤q3时，如图1（c）所示，L为切于弧的雷电流与弧的交点。弧为线路暴露弧，弧将被线路自身暴露弧所屏蔽，弧将被地线屏蔽弧所屏蔽。

4）当θ3＜ψ时，输电线路完全被地线所屏蔽，将再发生绕击。

1.2 暴露距离的计算

以铁塔底部中心为坐标原点建立坐标系，则A、B两点坐标分别为（xA，yA）、（xB，yB），均为与杆塔结构以及线路弧垂有关的参数，为已知值；lAB为地线与导线间距离。角a1、a2的计算公式分别为

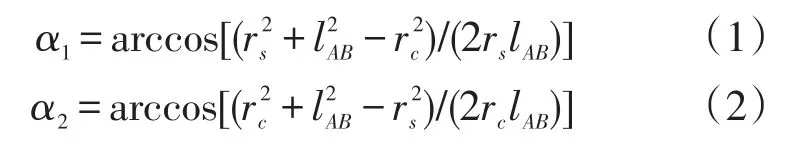
直线AM、BM的斜率及方程如式（3）-（6）所示：

通过求解直线AM、BM方程即可获得交点M的坐标（xM，yM）。设大地捕雷面方程为y=rg，联立直线BN方程可解得交点N的坐标（xN，yN）。

角θ1、θ2、θ3的计算公式分别为

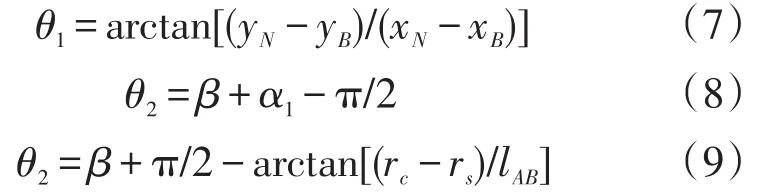
由于雷电入射方向不再固定，而暴露距离为暴露弧在垂直雷电入射方向上的投影，为一动态值。因此可将原坐标系进行旋转以方便暴露距离的计算。具体操作方法为：当雷电入射角y为正时，将原坐标系顺时针方向旋转y度；当入射角为负时，将原坐标系逆时针方向旋转|y|度。坐标系变换后的暴露距离计算公式如下：

1.3 绕击跳闸率

雷电流幅值概率计算公式采用我国一般地区计算公式[9]。输电线路绕击闪络率为

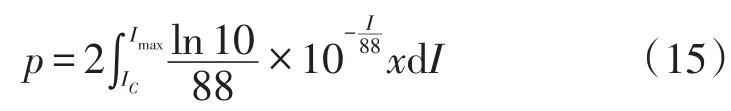
式中:Ic为起始绕击雷电流，Imax为最大绕击雷电流。输电线路绕击跳闸率为

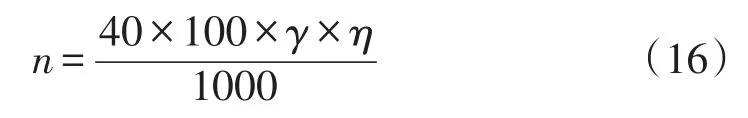
式中：γ为地面落雷密度；η为建弧率。

2 算例

2.1 参数选取

1）以国网通用设计中的220 kV酒杯塔2A3-ZBK为例，导线采用2×JL/G1A-300/25钢芯铝绞线，地线为JLB20A-150铝包钢绞线，绝缘子串含15片146 mm高度的瓷绝缘子，导线弧垂为15 m，地线弧垂为6 m。导线为水平排列，导、地线挂点高度分别为48.375 m、54 m，两边相导线以及地线对杆塔中心的水平距离分别为8.4 m、7.05 m。

2）起始绕击雷电流通过ATP-EMTP程序建模获取，其中杆塔模型采用Hara无损多波阻抗模型，绝缘子串闪络采用相交法进行判断。鉴于线路工作电压的影响，将一个工频周期等分为12个区间，分别计算各区间下的起始绕击雷电流。

3）导线、地线击距分别采用式（17）-（18）[17]，式中Uph为导线上工作电压瞬时值。

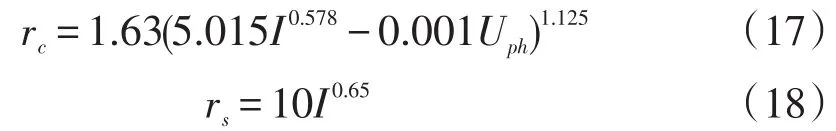
大地捕雷面离地面高度计算公式[17]为

最大绕击雷电流采用式（20）-（21）进行计算[20]，计算得到的最大电流为11.889 kA，其中rmax为最大击距。

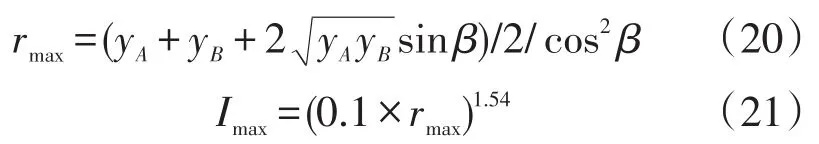
2.2 计算结果

利用式（16）计算各相角区间的绕击跳闸率，然后取其平均值作为输电线路的绕击跳闸率。经传统电气几何模型与改进模型计算得到的线路绕击跳闸率见表1。由该表可知，计及雷电入射角后，线路绕击跳闸率有所增大。

表1 两类模型的计算结果Table 1 Calculation results of these two models

2.3 两类模型计算结果的比较

该模型较传统模型的改进之处主要体现在雷电入射角及暴露距离两方面，现分别叙述如下。

1）在传统模型中，雷电入射只有垂直向下一个方向，也就是说其垂直入射的概率为1。而在本算例中，线路右侧导线的雷电入射角变化范围为-p/2至0.115 6（即6.624°），相应的入射概率为57.33%。可见，当考虑到雷电入射角后，由于地线屏蔽弧的屏蔽作用以及导线暴露弧自身的屏蔽作用（暴露弧与雷电流切点以上部分对暴露弧切点以下部分的屏蔽作用），降低了雷电入射至导线暴露弧的概率。

2）图2表示传统模型的暴露距离以及改进模型在不同雷电流幅值、不同雷电入射角下的暴露距离及其组成。针对改进模型，由图可知，①线路整体暴露距离主要由[-π/2，θ1]及[θ1，θ2]范围下的暴露距离组成，雷电入射角处于[θ2，θ3]下的暴露距离所占比重较小。②[θ2，θ3]范围下的暴露距离由于本身值比较小，随雷电流变化的趋势不明显，[-π/2，θ1]范围下的暴露距离随雷电流幅值增大而增大，而[θ1，θ2]范围下的暴露距离与雷电流幅值变化趋势相反。综合前述三者，整体暴露距离虽受雷电流幅值影响不稳定，但整体在5.0 m左右波动。对传统模型而言，其暴露距离的变化幅度很小，基本稳定在1.35 m左右。总的来说，改进模型的暴露距离要大于传统模型中的暴露距离。

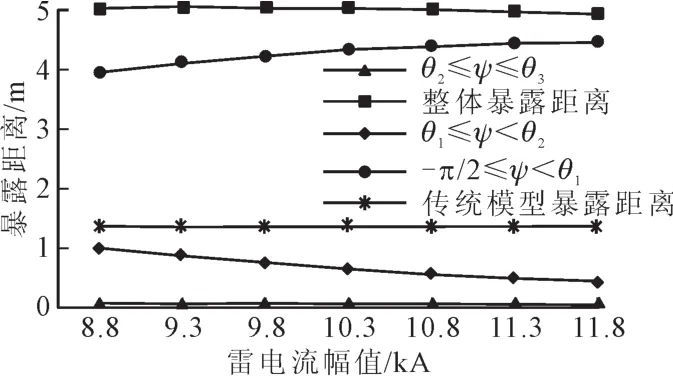
图2 暴露距离与雷电流幅值的关系Fig.2 Relationship between exposure distance and lightning current amplitude

计及雷电入射角模型更多地考虑到地线屏蔽弧及导线暴露弧的屏蔽作用，使得雷电入射至导线暴露弧的概率较传统模型有所降低，但由于计及入射角后的暴露距离增长幅度较大，使得经改进模型计算得到的输电线路绕击跳闸率要大于传统模型。

3 计及雷电入射角的电气几何模型有效性的验证

从表1可知，经计及雷电入射角模型计算得到的绕击跳闸率约是传统模型的4倍，而传统电气几何模型在实际工程中应用广泛，得到过大量验证。因此，有必要对本文模型的正确性进行验证。考虑到传统电气几何模型在输电线路大保护角下具有良好的适用性以及小保护角下精确性不足的特点，笔者将对比不同保护角下两类模型的计算结果从而进行验证。

当保护角变化范围在8～20°时，两类模型的计算结果如表2所示。由该表可知，改进模型计算得到的绕击跳闸率与输电线路保护角的变化关系与传统模型一致，都呈负相关关系，这侧面证明了改进模型的正确性。

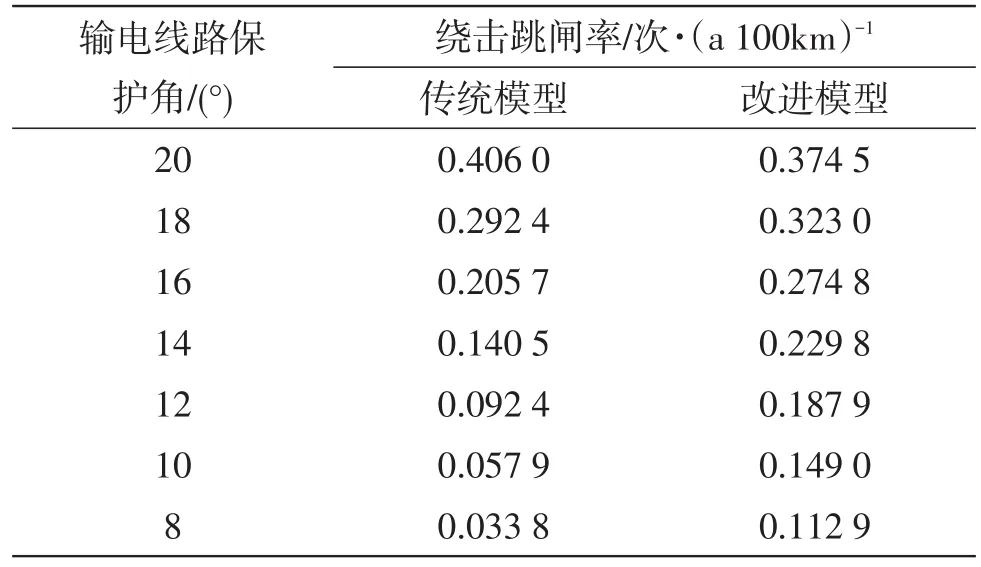
表2 不同保护角下两类模型的计算结果Table 2 Calculation results of these two models under different shielding angles

此外，将m作为评价两类模型计算结果偏差的指标，该指标的计算方法见式（22），式中n1、n2分别为经改进模型及传统模型计算得到的绕击跳闸率。指标m随保护角的变化趋势见图3，由该图可知，指标m随保护角的增大而减小，这表明当保护角较大时，改进模型计算得到的结果与传统模型比较接近；而当保护角比较小时，两类模型的计算结果存在较大偏差。

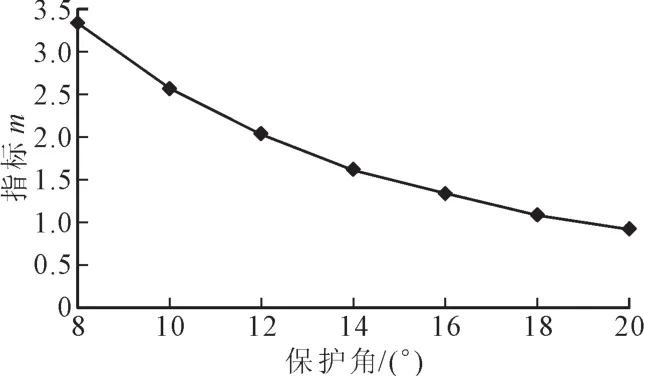
图3 指标m与保护角的关系Fig.3 Relationship between index m and shielding angles

目前对于输电线路小保护角尚无明确定义，规范建议单回220 kV输电线路保护角宜小于15°[19]。据此，笔者暂认为15°以下保护角为小保护角。当保护角在16～20°时，指标m变化范围为0.922～1.336；当保护角在8～14°时，指标m变化范围为1.636～3.341。可见，当为大保护角时，改进模型与传统电气几何模型计算得到的绕击跳闸率比较接近，说明改进模型是有效的；当为小保护角时，传统方法受限于雷电入射被固定为垂直向下，计算精度较低，而改进模型针对雷电入射方向进行了改进且其计算结果与保护角之间的变化关系符合实际，因此可认为改进模型在输电线路小保护角情况下同样具有较强的适用性。

4 结语

传统电气几何模型在计算输电线路小保护角或负保护角时，得到的绕击跳闸率偏小。笔者对雷电入射角及暴露距离进行了改进，使得计算更符合实际。

[1]司马文霞，杨庆，李永福，等.输电线路雷电绕击评估方法分析及展望[J].高电压技术，2015，41（8）：2500-2513.SIMA Wenxia，YANG Qing，LI Yongfu，et al.Analysis and prospect of lightning shielding failure evaluation meth⁃ods of transmission line[J].High Voltage Engineering，2015，41（8）:2500-2513.

[2]路永玲，刘洋，高嵩，等.江苏电网2005至2013年架空输电线路雷击跳闸率分析及防护[J].电瓷避雷器，2015（1）：49-53.LU Yongling，LIU Ynag，GAO Song，et al.Analysis of lightning trip and protection measures of overhead trans⁃mission lines in Jiangsu power grid from 2005 to 2013[J].Insulators and Surge Arresters，2015（1）:49-53.

[3]阮羚，谷山强，赵淳，等.鄂西三峡地区220kV线路差异化防雷技术与策略[J].高电压技术，2012，38（1）：157-166.RUAN Ling，GU Shanqiang，ZHAO Chun，et al.Technol⁃ogy and strategy of differentiated lightning protection for 220 kV transmission line in tree gorges area of western Hu⁃bei[J].High Voltage Engineering，2012，38（1）:157-166.

[4]杨玉，王思华，赵峰.基于蒙特卡罗法的输电线路绕击跳闸率的计算[J].电瓷避雷器，2016（1）：116-122.YANG Yu，WANG Sihua，ZHAO Feng.Calculation of transmission line shielding failure trip-out rate based on monte carlo method[J].Insulators and Surge Arresters，2016（1）:116-122.[5]赵淳，阮江军，李晓岚，等.输电线路综合防雷措施技术经济性评估[J].高电压技术，2011，37（2）：290-297.ZHAO Chun，RUAN Jiangjun，LI Xiaolan，et al.Technol⁃ogy and economy evaluation of comprehensive transmis⁃sion line lightning protection measures[J].High Voltage Engineering，2011，37（2）:290-297.

[6]江全才，魏飞翔，马骁旭，等.三峡近区500 kV输电线路差异化防雷技术研究[J].电瓷避雷器，2014（1）：61-67.JIANG Quancai，WEI Feixiang，MA Xiaoxu.Study on dif⁃ferentiation technology of lightning protection for 500 kV transmission line in Three Gorges Aera[J].Insulators and Surge Arresters，2014（1）:61-67.

[7]沈志恒，赵斌财，周浩，等.铁塔横担侧向避雷针的绕击保护效果分析[J].电网技术，2011，35（11）：169-177.SHEN Zhiheng，ZHAO Bincai，ZHOU Hao，et al.Analy⁃sis on effect of protecting transmission lines from shielding failure by sideward rods installed onto crossarm of towers[J].Power System Technology，2011，35（11）:169-177.

[8]王羽，陈昊，蓝磊，等.输电线路雷电屏蔽模拟试验影响因素[J].高电压技术，2014，40（3）：763-771.WANG Yu，CHEN Hao，LAN Lei，et al.Affecting factors of lightning shielding simulation test of transmission lines[J].High Voltage Engineering，2014，40（3）:763-771.

[9]DL/T 620—1997交流电气装置的过电压保护和绝缘配合[S].北京：中国电力出版社，1997.DL/T 620-1997 Overvoltage protection and insulation co⁃ordination for AC electrical installations[S].Beijing，Chi⁃na:China Electric Power Press 1997.

[10]YOUNG F S，CLAYTON J M，HILEMAN A R.Shielding of transmission lines[J].IEEE Transactions on Power Ap⁃paratus and Systems，1963，82（4）:132-154.

[11]吴广宁，熊万亮，曹晓斌，等.输电线路绕击特性的三维分析方法[J].高电压技术，2013，39（2）：374-381.WU Guangning，XIONG Wanliang，CAO Xiaobin，et al.Three-dimensional analysis method of shielding failure characteristics of transmission lines[J].High Voltage Engi⁃neering，2013，39（2）:374-381.

[12]姚陈果，王婷婷，杨庆，等.特高压交流输电线路绕击耐雷性能仿真分析[J].高电压技术，2013，39（3）：526-533.YAO Chenguo，WANG Tingting，YANG Qing ，et al.Simulated analysis of lightning shielding failure perfor⁃mance of UHVAC transmission lines[J].High Voltage En⁃gineering，2013，39（3）:526-533.

[13]吴炎彬，王云浩.基于先导法的输电线路耐雷水平研究[J].电瓷避雷器，2014（1）：115-119.WU Yanbin，WANG Yunhao，Study of transmission line lighting withstand level based on pilot method[J].Insula⁃tors and Surge Arresters，2014（1）:115-119.

[14]姚尧，李健，李涵，等.基于山区雷电先导发展的改进电气几何模型仿真研究[J].高电压技术，2015，41（5）：1550-1557.YAO Yao，LI Jian，LI Han，et al.Simulation research of improved electro-geometric model based on lightning lead⁃er development in mountainous terrain[J].High Voltage Engineering，2015，41（5）:1550-1557.

[15]孙义豪.1000kV/500kV同塔混压四回输电线路耐雷性能研究[D].重庆：重庆大学，2011.SUN Yihao.Study on lightning protection performance of quadruple-circuit transmission line with dual voltage 1000kV/500kV on the same tower[D].Chongqing，China:Chongqing University，2011.

[16]李瑞芳，吴广宁，曹晓斌，等.考虑雷电入射角后电气几何模型的改进[J].电瓷避雷器，2009（4）：23-26.LI Ruifang，WU Guangning，CAO Xiaobin，et al.Im⁃provement of electro-geometric model with considering lightning strike angle[J].Insulators and Surge Arresters，2009，（4）:23-26.

[17]彭谦，李军，卞鹏，等.改进电气几何模型法在1000kV输电线路雷电绕击跳闸率计算中的应用[J].电网技术，2010，34（9）：155-159.PENG Qian，LI Jun，BIAN Peng，et al.Application of im⁃proved electric geometry model in calculation of lightning shielding failure-caused trip-out rate of 1000 kV power transmission line[J].Power System Technology，2010，34（9）:155-159.

[18]吕政，郑皓元，杨庆，等.复杂地形下紧凑型输电线路绕击跳闸率计算方法[J].高压电器，2013，49（11）：117-122.LV Zheng，ZHENG Haoyuan，YANG Qing，et al.Calcu⁃lation method of shielding failure flashover rate of compact transmission line in complex terrain area[J].High Voltage Apparatus，2013，49（11）:117-122.

[19]GB 50545—2010 110 kV～750 kV架空输电线路设计规范[S].北京：中国计划出版社，2010.GB 50545-2010 Code for design of 110kV ～750kV over⁃head transmission line[S].Beijing，China:China Planning Press，2010

[20]李瑞芳，吴广宁，曹晓斌，等.山区输电线路雷电绕击跳闸率的计算[J].电网技术，2010，34（12）：142-146.LI Ruifang，WU Guangning，CAO Xiaobin，et al.Calcu⁃lation of shielding failure trip-out rate for transmission lines in mountain areas[J].Power System Technology，2010，34（12）:142-146.

An Improved Electrical Geometry Model Considering Lightning Strike Angle

GONG Lei，GUO Heng
（Chongqing Electric Power Design Institute，Chongqing，401121，China）

Electrical geometry model(EGM)based on exposure distance has several disadvantages such as the fixed direction of lightning strike and inapplicability to low or negative shielding angles of transmission lines.Therefore，the lightning strike mode is improved and its direction is extended to[-p/2，p/2]，the calculation method of exposure distance under different lightning strike angle is derived.In the case of low shielding angles，the shielding failure trip-out rate of traditional method and improved meth⁃od are 0.0217、0.0881 times/(100 km·a)，the causes are analyzed from lightning strike probability and ex⁃posure distance.The analysis shows that the lightning strike probability of improved method is 57.33%which is lower than traditional method，but its exposure distance which fluctuates around 5.0m is much bigger than 1.35m of traditional method.Besides，the shielding failure trip-out rates of these two modes under different shielding angles are calculated and the validity of improved method is proved based on their result.The improved EGM can overcome these disadvantages such as the fixed direction of lightning strike and inapplicability to low or negative shielding angles of traditional model.

transmission lines；lightning shielding failure；electrical geometry model(EGM)；light⁃ning strike

10.16188/j.isa.1003-8337.2017.06.016

2016-06-26

龚磊(1988—)，男，硕士，主要从事输电线路设计、线路防雷研究等工作。