基于单纯形法和Dijkstra算法下快递配送终端优化分析

孙 辉，王向前

（安徽理工大学 经济与管理学院，安徽 淮南 232001）

基于单纯形法和Dijkstra算法下快递配送终端优化分析

孙 辉，王向前

（安徽理工大学 经济与管理学院，安徽 淮南 232001）

以菜鸟驿站配送终端为例，分析其存在的配送问题，建立整数规划模型，选择运筹学中的单纯形法为基础，利用MATLAB软件对配送终端企业在人员安排上进行优化.采用最短路径Dijkstra算法对配送人员的路径进行研究，确定最优配送路径配送方案.

最后一公里；单纯形法；Dijkstra算法；配送优化

0 引言

在2016年11月11日全网购物狂欢节中，据星图大数据监测数据平台显示，截止12日凌晨全网总的销售额超过1 700亿元，邮寄包裹突破10亿个，其中东道主天猫以62.8%的网销份额约1 207亿元的销售额占据销售榜单第一名的位置［1］.但是庞大的经济效益现象下传统快递配送模式却面临着配送时效性差、货件破损率高、配送脱节甚至爆仓等一系列问题［2］.这些问题都在时刻考验着配送终端企业的市场生存能力.当前以B2B（Business to Business）以及B2G（Business to Government）的终端配送模式中，由于存在特定配送渠道和方法能够确保货物快速、安全以及高效的送达［3］.然而以B2C（Business to Consumer）和C2C（Consumer to Consumer）为绝大多数的终端配送模式，却因为退换货繁琐、配送不到位、配送人员素质不高和配送等待时间较长等一系列因素制约着其快速发展.根据有关权威统计机构数据披露，传统的终端商业配送中约30%运输成本在“最后一公里”配送中产生，而最终有80%终端配送效率发生在该环节中.对于传统配送企业来说配送时间、成本以及效率无疑已经成为配送终端和配送人员的稀缺资源，如何进行配送终端的优化已经迫在眉睫［4］.文献［5］运用禁忌搜索算法和贪婪插入算法建立车辆最小行驶费用和订单惩罚费用数学模型，研究电子商务中订单的配送优化问题，提高了车辆的使用效率问题和降低了订单的配送时间问题.在基于启发式算法的几何分析中，文献［6］利用二次搜索对区域终端配送问题建立VRP策略模型，解决配送时多次补货的路径优化问题.文献［7］使用动态规划以及贝尔曼最优原理将配送终端分解为多个阶段，使用矩阵运算的方式确定配送路线最优化方法.本文运用单纯形法和Dijkstra最短路径法对配送终端在人员的配送安排以及配送路径选择进行优化，对配送终端所存在的问题进行具体的优化处理，从而使得快递企业在配送时间问题上得到了有效控制以及降低了配送成本，从而提高了快递企业运作效率.

1 实际问题的引入及数学模型的建立

在电子商务的快速推动下，快递配送企业在配送效率面前的短板越来越引起人们的重视.本文通过实地调研的方式以菜鸟驿站快递配送企业为研究对象，分析快递包裹配送时人员配置和路径选择所存在的问题，进而从企业层面和配送人员角度两个层次分别进行配送优化，继而通过合理安排限制资源使配送效益达到最优化的状态.为了使模型尽量简化，去除一些非必要影响因素把配送终端企业人员的配送问题进行了如下描述：菜鸟驿站快递配送企业每天的配送人员需求量如表1所示，由于快递行业的特殊性，为了确保快递配送人员的充分休息，该公司规定快递配送人员每周有连续两天的调休制度.

表1 快递配送终端人员需求

其中，部分快递配送人员的配送路线图如图1所示.

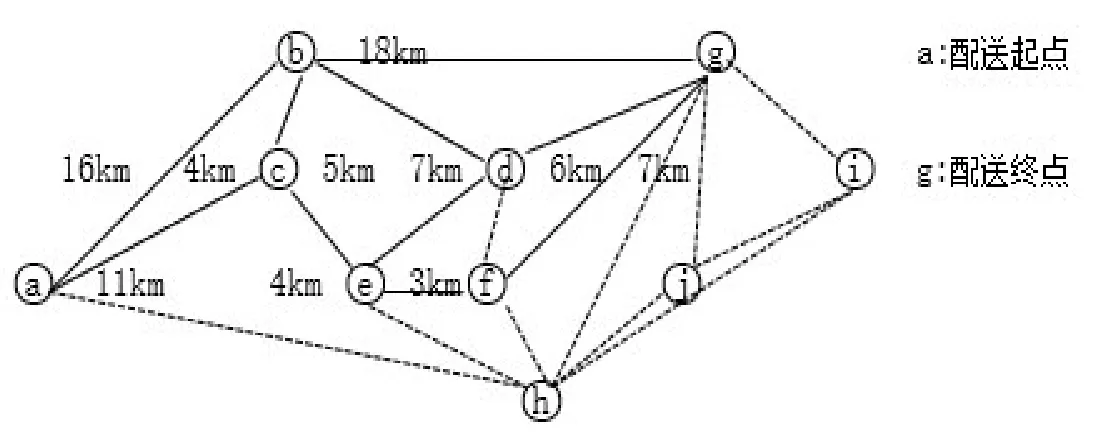
图1 配送人员路径图

图1 为部分配送人员的配送路线图，起始点a为菜鸟驿站终端配送原点，g点为配送终点.图1上标注具体距离的实线部分是配送员可能选择的配送路径，虚线部分为该类配送员未选择过的路径，图1中并未标注这部分路径的实际距离.

1.1 基于单纯形法配送终端人员调度安排

1947年Dantzing在研究前人在线性规划问题方面的方法，创建了处理线性规划问题的单纯形法，其理论依据为在可行域是n维向量空间的Rn多面凸集中，若线性规划问题存在最优解的情况其必在Rn多面凸集的某顶点处，线性规划问题对应的基本可行解一定在顶点处达到.

设线性规划问题的标准形式为：minf(X)=minCX，其中

同时，令

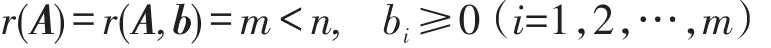
将标准式进行向量变换：

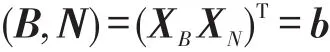
即

将公式（1）（2）变换可得：

将线性规划中的基本可行解X0所对应的分量…,σm≤0时，则基B所对应的基本可行解X0及充要条件为：

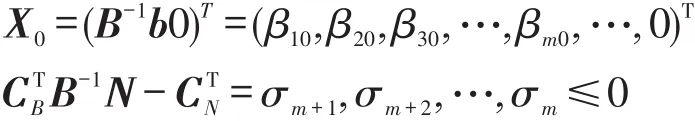
当∃σm+1,σm+2,…,σm≥0，则原方程没有最优解，需要找到另一个基本可行解X1，使得f(x1)≤f(x0)存在.其基本思想是：先对其中一个基本可行解进行判断，发现该基本可行解是否是线性规划问题中的最优解.若不是则按照线性规划转换方法，找到另一个改进后的基本可行解进行判别.以此往复不断进行，直到在有限个基本可行解中找出线性规划问题的最优解.

将表1中的问题转化形成整数规划模型并进行求解为：

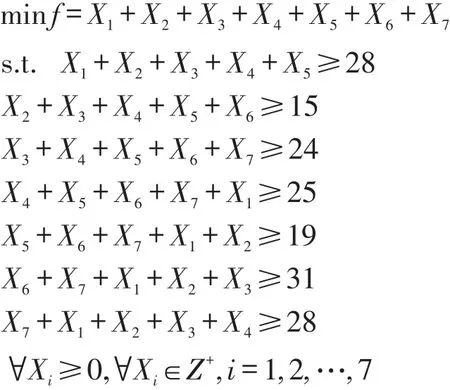
将约束方程加入松弛变量si,i=1,2,…,7变成标准形式，则上述整数规划问题的系数矩阵A，约束右端向量b，目标函数系数向量C分别为：

调用MATLAB中的SimpleMthd函数，调用格式为：

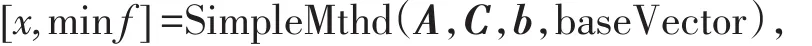
其中A，C，b，baseVector分别为方程的约束矩阵、目标函数系数向量、约束右端向量及初始基向量.可以得到X1=12,X2=0,X3=11,X4=5,X5=0,X6=8,X7=0，目标函数的最小值为36，即配送终端可以安排36个快递配送人员，其中有12个人在星期一和星期二调休，11个人在星期三和星期四休息，5个人在星期四和星期五休息，8个人在周六和周日休息.这样的调休制度不仅能够满足日常的配送要求，还使得配送人员总数达到最小化，降低了配送终端的人力资本耗费.

1.2 基于Dijkstra最短路径法下的配送人员路径优化

1959年计算机科学家狄克斯特拉在研究路径优化时提出了最短路径的算法，又称双标号法.即对图中的点Qj赋予两个标号(lj,kj)，第一个标号lj为起点Qs到点Qj的最短距离，第二个标号kj表示点Qs到点Qj的最短距离上Qj前面一个邻点的下标，发现点Qs到点Qj最短距离，其基本步骤［8］：

（a）给起点Q1以标号(0,s)，表示点Q1为起点，起始距离为0；

（b）列出所有以标号的点集合I和未标号集合J以及弧集合T={(Qi,Qj)|Qi∈I,Qj∈J}；

（c）若弧的集合T=∅则计算结束，若点Qt标号(lt,kt)，则点Qs到点Qt的最短距离为lt，如果点Qt未标号，则不存在这样的有向路，若T=∅，则计算T中的每一条弧sij=li+cij.在所有的sij中找出最小的弧(Qc,Qd)并令其标号(scd,c).

Dijkstra算法在求网络中的其中某个源节点到其余节点时，核心就是从未标记的点中选择一个权值最小的弧［9］.

将图1配送人员路径进行优化，其步骤为：

1）给予起始点a标号(0,s)，I={a},J={b,c,d,e,f,h,g}边的集合{[Qi,Qj]|Qi,Qj其中一点属于I，另一个属于J}={[a,b],[a,c]}，并有：s12=l1+c12，即s12=0+16=16，s13=l1+c13=11，min(s12,s13+s13)=11.给边[a,c]中的未标号的点c标以（11，1）表示从a到c的距离为11，且在a到c的最短路径上c前面的点为a点.

2）I={a,c},J={b,d,e,f,g}，边集合 {[a,b],[c,b],[c,e]}，则s32=l3+c32=15，s35=l3+c35=16，min(s13,s32,s35)=15，将b以标号（15，3）.

3）同理可得c（11，1），d（20，5），e（16，3），（f18，5）标号.

4）此时I={a,b,c,d,e,f},J={g}，边集合 {[Qi,Qj]|Qi,Qj其中一点属于I，另一个属于J}={[b,g],[d,g],[f,g]}，则s47=l4+c47=25，min(s27,s47,s67)=24，g点标号（24，6）.

5）最后I={a,b,c,d,e,f},J=∅，边集合{[Qi,Qj]|Qi,Qj其中一点属于I，另一个属于J}=∅计算结束，得出最短配送路径依次为a→c→e→f→g，最短配送距离为22 km.

在通过对配送人员路径优化后可以帮助配送人员在路径选择中提供参考，克服以往配送时以经验为主导的配送模式，节约了配送成本以及调高了配送效率，对于配送人员来说时间日益成为配送中的稀缺资源，通过路径优化降低了时间和距离成本对配送人员的影响.

2 总结

随着我国快递行业的不断发展，传统式的配送模式终将会被行业淘汰.终端配送企业会运用更为先进的管理理念和方法不断地对配送效率进行优化［10］.如何将电子商务的“最后一公里”配送成本与效率达到最优化是配送企业一直关注的问题.通过利用运筹学中的单纯形法以及Dijkstra最短路径法对配送终端的具体问题建立数学模型，以对配送企业和配送人员两个方面进行优化.对于配送企业可以进一步规范配送模式，降低人力资源的浪费以及做到配送成本的最优，对于终端配送人员则可以通过优化配送路径达到配送效率最大化，提高作业效率.

［1］李芳.2016年11月12日全网销售总额统计［N］.重庆商报，2016-11-12（4）.

［2］谭述芳.我国快递配送最后一公里问题研究［J］.商业时代化，2015（3）：62-64.

［3］AIZED Tauseef.Hierarchical modelling of last mile logistic distribution system［J］.The International Journal of Advanced Manufacturing Technology，2014，70（5）：1053-1061.

［4］薛开源，蒋惠西，顾传进，等.快递配送终端优化研究［J］.物流技术，2016（2）：42-44.

［5］李琳，刘士新，唐家福.电子商务中订单配送优化模型及两阶算法［J］.系统工程学报，2011（2）：237-243.

［6］刘向，李延晖.电子商务配送的跨区域VRP模型及其启发式算法［J］.清华大学学报（自然科学版），2006（S1）：1014-1018.

［7］杨茂盛，李琦.基于动态规划的物流配送优化研究［J］.商场现代化，2007（11）：128.

［8］韩伯棠.管理运筹学［M］.北京：高等教育出版社，2009：85-115.

［9］王志和，凌云.Dijkstra最短路径算法优化及其实现［J］.微计算机信息，2007（33）：275-277.

［10］唐倚智.B2C电子商务物流的挑战和趋势［J］.物流技术与应用，2012（9）：66-68.

Optimization Analysis of Express Delivery Terminal Based on Simplex and Dijkstra Algorithm

SUN Hui，WANG Xiangqian
（School of Economics and Management，Anhui University of Science&Technology，232001，Huainan，Anhui，China）

Taking the rookie terminal distribution as an example，the paper analyzes the existence of the distri⁃bution problems.The linear integer programming model is established.Based on the simplex method in the research，the software of the distribution terminal is optimized by the MATLAB software.Finally，the shortest path Dijkstra algorithm is used to study the routing of the distribution personnel to determine the optimal dis⁃tribution route distribution scheme.

last mile；simplex method；Dijkstra algorithm；distribution optimization

C 936

A

2095-0691（2017）03-0049-04

2017-04-26

孙 辉（1993- ），男，安徽寿县人，硕士生，主要研究方向：物流与供应链.