基于马氏度量的图像谱特征描述

张诗清，鲍文霞，2，余国芬

（1.安徽大学电子信息工程学院，安徽 合肥 230601；2.偏振光成像探测技术安徽省重点实验室，安徽 合肥 230031）

基于马氏度量的图像谱特征描述

张诗清1，鲍文霞1，2，余国芬1

（1.安徽大学电子信息工程学院，安徽 合肥 230601；2.偏振光成像探测技术安徽省重点实验室，安徽 合肥 230031）

传统的谱特征描述过程中采用的是不能反映样本间潜在关系的欧式距离进行度量的.为更好地区分数据之间的联系，提出基于马氏度量的图像谱特征描述算法.首先，对特征点及其周围特征点按照马氏距离进行分层，并在每层上面构造相应的结构图及计算其关联矩阵；接着，对关联矩阵进行谱分解得到其特征值向量和谱隙向量；然后分别用两者的最大值、平均值和方差统计量得到最终的马氏度量谱特征；最后，根据马氏度量谱特征之间的相似性和特征点之间距离关系来构建匹配数学模型，并用贪心算法求解得到特征点之间的匹配关系.实验结果表明，该算法提高匹配精度；同时将其应用于偏振图像的匹配问题上，并取得较好的匹配结果.

谱特征描述；马氏度量；马氏度量谱特征；偏振图像

0 引言

图像特征匹配是图像处理、计算机视觉、模式识别等领域中一项基本但非常困难的任务，对获取的特征点进行特征描述是匹配的一个重要步骤.近年来，谱图理论［1］广泛应用于特征描述中，从而得到一种谱特征描述.Scott［2］和Shapiro［3］最早将谱图理论用于构造特征描述中，首先根据图像特征点之间的欧式距离来构造邻接矩阵，然后进行谱分解来得到谱特征描述，最后根据谱特征之间关系来获得匹配关系；王年等［4］提出一种图的Laplace谱，首先根据特征点集构造规范化Laplace矩阵，接着对该矩阵进行谱分解得到其特征向量用来构造Laplace谱，最后用匹配来验证所构造的Laplace谱提高匹配精度；唐俊等［5］提出一种多谱特征描述子，通过对构造图的不同矩阵求解得到特征值序列，然后对这些特征值序列通过多谱嵌入技术得到最终的局部结构描述子；Tang等［6］构造谱上下文描述子，首先根据特征点及其邻域特征点来构造图，然后对图计算矩阵并进行谱分解，最后用特征值来得到谱上下文描述子，匹配结果表明该描述子对位置抖动以及出格点具有较好的鲁棒性；朱明等［7］将特征点的邻域点进行分层，并基于灰度信息在每层上构造线图，然后通过对图的赋权邻接矩阵进行谱分解得到特征值，最后将每层得到的邻接谱结合得到最终的谱特征，该谱特征对噪声具有较高的鲁棒性；Yan等［8］提出一种对亮度变化具有鲁棒性的单调强度不变描述子，对有向图的无符号Laplace矩阵进行谱分解得到特征值向量及其谱隙向量，从而构造描述子.

上述这些谱特征的构造都是基于欧式距离进行度量的，欧式距离假设样本空间是各向同性的，但这种假设在实际应用中是不成立的，因为它没有充分体现样本维度分量之间所包含的潜在联系.因此，为使构造的谱特征描述能满足实际应用情况，本文引入对样本数据具有更好区分性的马氏度量来代替欧式距离，从而提出一种基于马氏度量的图像谱特征描述算法.首先，对特征点按照距离关系进行分层并在每层上面构造结构图；然后，对结构图的邻接矩阵进行谱分解，从而得到其马氏度量谱特征；最后，构造匹配数学模型，并用贪心算法求解得到匹配关系，从而验证本文所提的基于马氏度量的图像谱特征的性能.

1 马氏度量谱特征描述

1.1 马氏度量

马氏度量（Mahalanobis distance）是1936年由印度统计学家Mahalanobis提出的，它充分考虑样本数据维度分量之间的相关性，即考虑样本数据分布的统计特性—协方差矩阵，常用于计算两个未知样本数据之间相似度.马氏度量具有3个性质，分别为平移不变性、旋转不变性和仿射不变性.

对于由n个样本构成的样本空间X={xz:1≤z≤n}⊂Rn，其均值向量和协方差矩阵分别记为uX和CX，其各自的计算公式如下：

其内任意两个样本点xa和xb之间的马氏距离为：

马氏度量满足度量公理，即同时满足如下4个条件：

1）非负性：dM(x,y)≥0；

2）同一性：dM(x,y)=0⇔x=y；

3）对称性：dM(x,y)⇔dM(y,x)；

4）三角不等式：dM(x,z)≤dM(x,y)+dM(y,z).

1.2 谱特征描述

在图像中将像素点作为节点，节点之间的相互关系作为边来构造图.假设有点集P，记点集P={pi,i=1,2,…,t}，首先对点集P构造结构图，任意两点之间的距离关系作为连接两点边的长度，这样就可以得到一个t阶的结构图.点集P中的任意一点pi有t-1个点与其相连，即有t-1条边与pi相连并可以构造星图Si，边分别记之为：e1≤e2≤…≤et-1（按照大小顺序进行排列）.

其次，求解Si的线图Li［9］，就是将边转换为点的过程.线图中的点就是星图中的边，点连接的是原星图中对应关联的边，如图1所示.pi的星图如图1（1）所示，其中e1、e2、e3是与pi相关联的边，长度分别为1、2、3；构造的线图如图1（2）所示，e1、e2、e3作为点，边的权值分别为e1、e2、e3之间差的绝对值.

最后，根据线图构造邻接矩阵.在一幅大小为m×n的图像I上取非边界点u，u的特征可以由u及其邻域点的属性之间的相互关系来表示.设u的i个邻域点为x1,x2,…,xi，i=1,2,…,t(t=(2n+1)2-1,n=1,2,…,t)，构造星图S1，即u和所有邻域点相连，边uxi的权值ri=| |u-xi，i=1,2,…,t.对星图S1求解线图L1，对线图L1构造赋权邻接矩阵H，其元素为：

其中，|.|表示一种距离度量.

H是一个对称的、半正定的矩阵，因此对H进行谱分解得到：

其中，Δ=diag(λ1,λ2,…,λt)，其对角元素是H特征值的降序排列，U={U1,U2,…,}Ut是正交特征向量集合.因此，可以将特征值向量(λ1(u),λ2(u),…,λt(u))或者特征向量组合(U1,U2,…,Ut)作为点u的谱特征.

1.3 马氏度量谱特征描述

对于图像中任意特征点xi的特征属性，可以通过该点以及其周围特征点之间的关系来进行描述.假设I和J是两幅待匹配的图像，其中分别包含有s和s′个特征点，分别记为点集P={x1,x2,…,xs}和点集Q={y1,y2,…,ys′}.点集P中任一特征点xi的马氏度量谱特征描述如下：

首先，在点集P中计算平均最小马氏距离d，并根据平均最小马氏距离定义半径集R={|

rφrφ=φd,φ=1,2,…,5}，其中平均最小马氏距离计算如下：

以xi为圆点，rϕ∈R为半径在点集P上选择特征点来构成子点集Ωiϕ，即Ωiϕ={xl:xl∈PanddM(xi,xl)＜rϕ}.

其次，对子点集Ωiϕ构造无向加权图，并计算其关联矩阵为：

其中：β是常数因子，用来控制特征点之间的相互作用.

对关联矩阵Hiφ进行SVD分解可得：

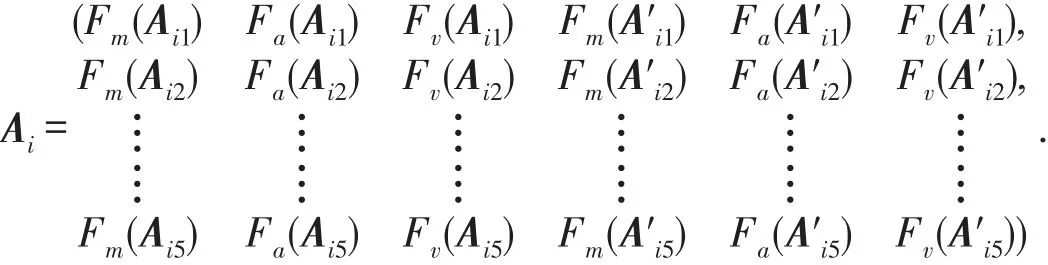
对特征值向量和谱隙向量分别计算其最大值、平均值和方差3个统计量来获得固定长度的马氏度量谱特征，从而避免长度不等的向量比较问题.对特征值向量Aiϕ进行统计量计算如下：

同样，可以计算得到谱隙向量A′iϕ的3个统计量Fm(A′iϕ)、Fa(A′iϕ)、Fv(A′iϕ). 最终，用一个30维的特征向量来表示特征点xi的马氏度量谱特征，即

2 特征匹配

将上述所构造的马氏度量谱特征应用于特征匹配上来检验其性能，具体的匹配过程如下.对于点集P和Q中的特征点ui和vj，其马氏度量谱特征分别记为Ai和Bj，则可以定义如下的匹配关系矩阵M，其中Ai和Bj之间的相似性关系定义为对角元素Mij,ij，非对角元素Mij,i′j′表示特征点之间的几何距离，计算公式如下：

因此，对上述构造的匹配关系矩阵用匹配数学模型［10］来求解，求得分配向量x*，使下式的目标函数最大化：

其中：x∈{0,1}ss′×ss′是表示匹配关系的匹配向量.当x=1时表示匹配，否则x=0时表示不匹配，从而得到特征点集P和Q之间的匹配关系.

最后用贪心算法［11］求解该匹配的数学模型，得到匹配结果.

3 实验结果与分析

3.1 基于马氏度量的图像谱特征实验结果与分析

为验证本文提出的基于马氏度量的图像谱特征的性能，本文在CMU/VASC图像数据库的long-hotel序列图像上进行图像匹配实验，下面给出部分的实验结果.本文取第10、30、50、70、90帧图像分别与第1帧图像进行匹配，首先在每帧图像上提取40个特征点，然后分别用本文提出的算法与文献［5］、文献［11］以及文献［12］的算法进行对比实验，实验结果如图2所示，图2（a）-（c）分别表示第10、50、70帧与第1帧进行匹配的实验结果.表1给出具体的实验数据.实验结果表明，本文提出的基于马氏度量的图像谱特征的匹配精度最高，当帧差数达到90帧时仍然能够达到100%的正确匹配率；而其他3种算法的准确率随着帧差数的增加逐渐下降.

图2 图像匹配实验结果

表1 实验的匹配数据

3.2 偏振图像匹配实验结果与分析

本文将所提出的基于马氏度量的图像谱特征描述算法应用于偏振图像匹配中，下面给出部分的实验结果.首先，分别取近景和远景采集所需的偏振图像数据；然后，在每张图像上提取40个特征点，接着用本文提出的基于马氏度量的图像谱特征对特征点进行特征描述，最后用本文提出的特征匹配算法进行图像匹配.实验结果如图3所示，其中（a）是近景图像及其匹配结果，（b）是远景图像及其匹配结果.从实验结果可知，对近景和远景的偏振图像进行匹配时都达到100%的匹配正确率，因此表明本文提出的基于马氏度量的图像谱特征描述能够有效地描述图像特征.

图3 偏振图像匹配实验结果

4 结论

文中提出一种基于马氏度量的图像谱特征描述算法，该算法在图像谱特征描述过程中用马氏度量代替欧式距离进行度量，并利用特征点之间的位置关系来获得谱特征向量以及谱隙向量，最后用两者的统计量来定义马氏度量谱特征.实验结果表明，本文提出的基于马氏度量的图像谱特征在匹配问题上具有较高的匹配精度，并且在偏振图像匹配问题上具有较好的效果.

［1］CHUNG FAN R K.Spectral graph theory［M］.Washington D C：American Mathematical Society，1997.

［2］SCOTT G L，LONGUET-HIGGINS H C.An algorithm for associating the features of two image［J］.Proc of Royal Society of London：Biological B，1991 ，244（1309）：21-26.

［3］SHAPIRO L S，BRADY J M.Feature-based correspondence：an eigenvector approach［J］.Image Vision Computing，1992，10（5）：283-288.

［4］王年，范益政，韦穗，等.基于图的Laplace谱的特征匹配［J］.中国图象图形学报，2006，11（3）：332-336.

［5］唐俊，刘志忠，梁栋，等.基于多谱特征表示的点模式匹配算法［J］.光学学报，2013，33（12）：154-161.

［6］TANG Jun，SHAO Ling，ZHEN Xiantong.Robust point pattern matching based on spectral context［J］.Pattern Recognition，2014，47（3）：1469-1484.

［7］朱明，梁栋，范益政，等.基于谱特征的图像匹配算法［J］.华南理工大学学报（自然科学版），2015，43（9）：60-66.

［8］YAN Pu，LIANG Dong，TANG Jun，et al.Local feature descriptor invariant to monotonic illumination changes［C］∥SPIE，2016，013023：1-12.

［9］朱明，梁栋，唐俊，等.基于线图Q-谱的点模式匹配算法［J］.华南理工大学学报（自然科学版），2011，39（7）：102-108.

［10］MINSU C，JIAN S，OLIVIER D，et al.Finding matches in a haystack：a max-pooling strategy for graph matching in the presence of outliers［C］∥Proc of Computer Vision and Pattern Recognition，2014：2091-2098.

［11］LEORDEANU M，HEBERT M.A spectral technique for correspondence problems using pairwise constraints［C］∥Proc of International Conference on Computer Vision，Beijing，IEEE，2005：1482-1489.

［12］梁栋，童强，王年，等.一种基于Laplacian矩阵的图像匹配算法［J］.计算机工程与应用，2005，36：31-32.

Image Spectral Feature Description Based on Mahalanobis Metric

ZHANG Shiqing1，BAO Wenxia1，2，YU Guofen1
（1.School of Electronics and Information Engineering，Anhui University，230601，Hefei，Anhui，China;2.Key Laboratory of Polarization Imaging Detection Technology Anhui Province，230031，Hefei，Anhui，China）

The traditional spectral features in the process of description use the European distance metric that can not reflect the potential relationship between the samples.In order to better distinguish the relation be⁃tween data，the image spectral feature description algorithm based on mahalanobis metric is proposed in this paper.Firstly，the feature points and their surrounding points are layered according to the Mahalanobis dis⁃tance，and the corresponding structure graph is constructed on each layer and the correlation matrix is calcu⁃lated.Secondly，the eigenvalue vector and the spectral gap vector are obtained by spectral decomposition of the correlation matrix.And then，the maximum，mean and variance of the two vectors are calculated respective⁃ly to obtain the final mahalanobis metric spectral features.Finally，a matching mathematical model is con⁃structed based on the similarity between the mahalanobis metric spectral and the distance between feature points，and the matching relation between feature points is obtained by greedy algorithm.A large number of experimental results show that the proposed algorithm improves the matching accuracy.At the same time，it is applied to the matching of polarimetric images and a good matching result is obtained.

spectral feature description；Mahalanobis metric；Mahalanobis metric spectral feature；polarimetric image

TP 391.9

A

2095-0691（2017）04-0038-06

2017-06-13

国家自然科学基金项目（61401001，61501003）；安徽省重点实验室开放基金项目（2017KJQ010001）；安徽大学2016年大学生科研训练计划资助项目

张诗清（1997- ），女，安徽安庆人，研究方向为图像处理.通信作者：鲍文霞（1980- ），女，安徽铜陵人，副教授，研究方向为图像处理、计算机视觉方向等.