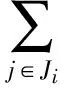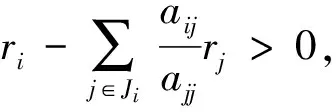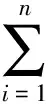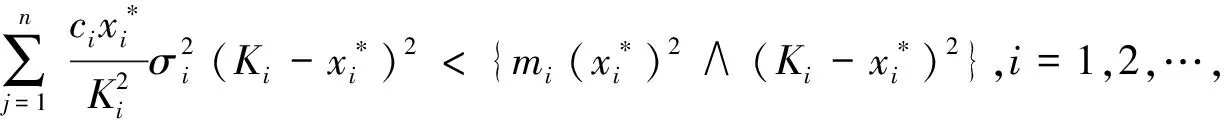随机多种群竞争系统的渐近行为

李海红，李海霞

(1.吉林建筑大学基础科学部，吉林 长春 130024； 2.长春光华学院商学院，吉林 长春 130033)

·研究简报·

随机多种群竞争系统的渐近行为

李海红1，李海霞2

(1.吉林建筑大学基础科学部，吉林 长春 130024； 2.长春光华学院商学院，吉林 长春 130033)

研究了随机Lotka-Volterra多种群竞争系统.利用构造Lyapunov函数的方法证明了系统正解的存在唯一性，并得到了系统存在不变分布，具有遍历性.

Lyapunov函数；伊藤公式；存在唯一性；遍历性

众所周知，竞争是生态系统[1-3]中种群之间的重要关系之一，Lotka-Volterra竞争系统可描述为

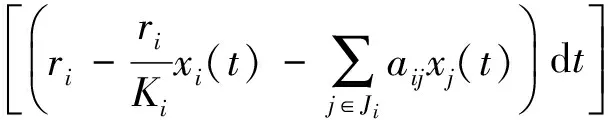
(1)

其中：xi是第i个种群的密度，ri是第i个种群的内禀增长率，Ki是第i个种群对环境的容纳量.这里考虑到环境白噪声的影响，令aii=ri/Ki，则上式变为

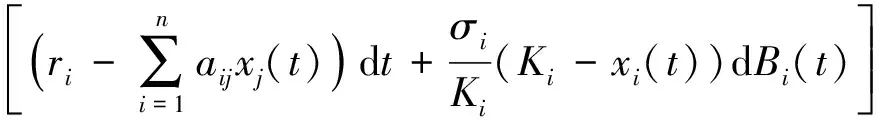
(2)

1 系统正解的存在唯一性

研究种群系统的动力学行为，首先考虑系统是否存在全局解.本文采用文献[4-5]中的方法证明了系统(2)存在唯一的全局正解.

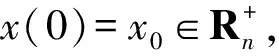
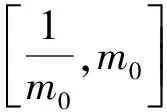
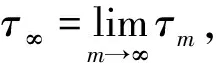
P{τm≤T}≥ε.

(3)

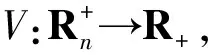
由伊藤公式可得

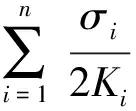
其中

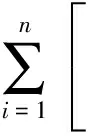
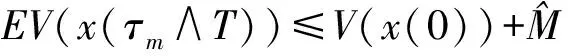
(4)

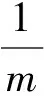
其中1Ωm表示Ωm的特征函数.令m→∞，得到矛盾.因此τ∞=∞ a.s..定理1证毕.

2 系统存在平稳分布且具有遍历性

下面给出系统(2)存在平稳分布且具有遍历性的结果.

定理2令x(t)是带有初始条件0

且

根据文献[6]有

从而

这表明文献[6]中引理3.2的条件(B2)满足，从而解x(t)在区域U是常返的，结合文献[6]中引理3.3和注3.3，x(t)在任意有界区域D⊂D0是常返的.另外，∃M：∀D，

满足

从而文献[6]中引理3.2的条件(B1)满足.因此系统(2)存在平稳分布μ(·)，且是遍历的.

[1] 高芳.带有食饵避难的Leslie-Gower捕食者-食饵扩散系统的稳定性及最优税收[J].东北师大学报(自然科学版)，2014，46(2)：1-8.

[2] GOH B S.Global stability in many species system[J].Amer Nat，1997，111： 135-143.

[3] XIA P Y.Persistence and nonpersistence of a nonautonomous stochastic mutualism system [J/OL].Abstract Appl Anal， 2013[2016-11-07].Article ID 256249.

[4] MAO X，MARION G，RENSHAW E.Environmental noise suppresses explosion in population dynamics[J].Stochastic Process Appl， 2002，97： 95-110.

[5] JIANG D Q，ZHANG B X.Existence uniqueness，and global attractivity of positive solutions and MLE of the parametres to the logistic equation with random perturbation[J].Science in China，2007(7)： 977-986.

[6] JIANG D Q，JI C Y，LI X Y，Analysis of autonomous Lotka-Volterra competition systems with random perturbation [J].Math Anal Appl， 2012，390： 582-595.

Theasymptoticbehaviorofastochasticmulti-competitivesystem

LI Hai-hong1，LI Hai-xia2

(1.Department of Basic Science，Jilin Construction University，Changchun 130024，China； 2.School of Business，Changchun Guanghua University，Changchun 130033，China)

An-species competition system with stochastic perturbation is considered.First，by using the method of constructing Lyapunov function，the unique positive solution of the system is proved.Then，the existence of the stationary distribution of the system is given，which implies the system is ergodicity.

Lyapunov function；Ito formula；existence and uniqueness；ergodicity

1000-1832(2017)04-0158-03

10.16163/j.cnki.22-1123/n.2017.04.028

2016-11-07

国家自然科学基金资助项目(11171350).

李海红(1983—)，女，博士，主要从事微分方程研究.

O 211.63学科代码110·44

A

(责任编辑：李亚军)