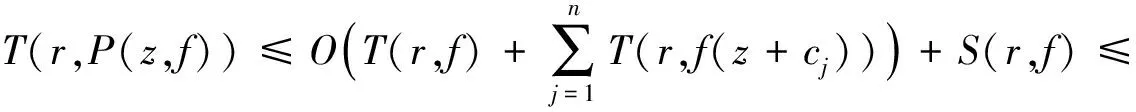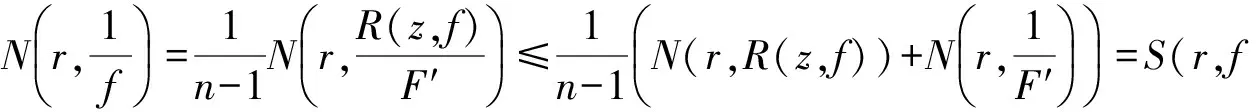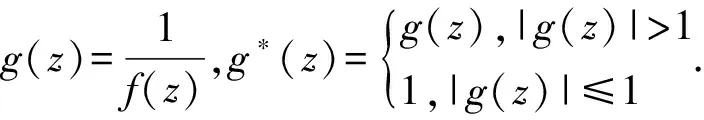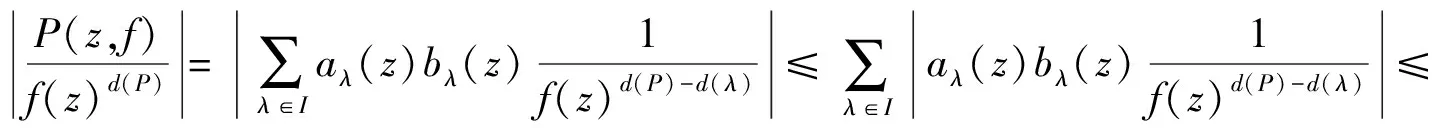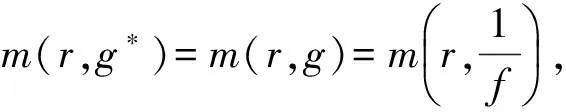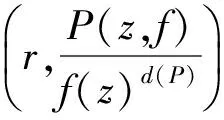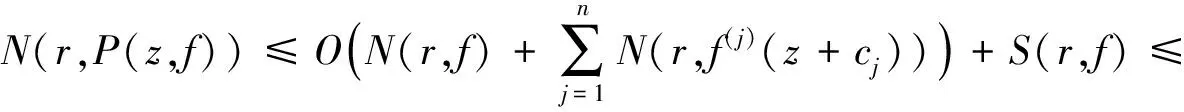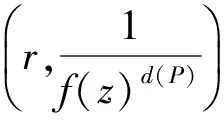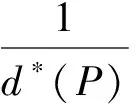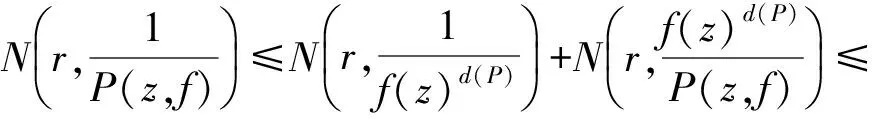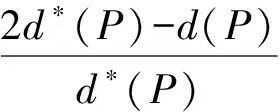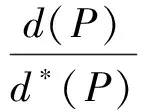复差分多项式的亏量
2017-12-19赵浩岚
金 瑾,赵浩岚
(1.贵州工程应用技术学院数学系,贵州 毕节 551700;2.贵州工程应用技术学院循环经济研究院,贵州 毕节 551700;3.上海金融学院国际经贸学院,上海 201209)
复差分多项式的亏量
金 瑾1,2,赵浩岚3
(1.贵州工程应用技术学院数学系,贵州 毕节 551700;2.贵州工程应用技术学院循环经济研究院,贵州 毕节 551700;3.上海金融学院国际经贸学院,上海 201209)
利用亚纯函数的Nevanlinna值分布理论,研究了差分多项式的亏量问题,得到了关于有限级亚纯函数差分多项式亏量的一些结果,其中部分结果可视为微分多项式相应结果的差分模拟,这些结果推广了前人已有的结论.
差分多项式;亚纯函数;有限级;亏量
1 主要结论
假定读者熟悉Nevanlinna关于亚纯函数值分布理论的标准记号和主要结果,如:m(r,f),N(r,f),T(r,f),δ(a,f)等.[1-20]
近年来,许多学者致力于研究亚纯函数不同微分表达式的值分布问题,并得到了丰富的结果.[1-6]特别地,Hayman[3]研究了亚纯函数及其导数的Picard例外值,得到以下结论:
定理A设f(z)是超越整函数.则:
(ⅰ) 当n≥3且a≠0时,Ψ(z)=f′(z)-afn(z)无穷多次取到任意有限复数;
(ⅱ) 当n≥2时,Ψ(z)=f′(z)fn(z)无穷多次取到任意有限非零复数.
随后,文献[5]考虑了微分多项式的亏量问题,对定理A进行了推广,得到下面结论.
定理B设f(z)是超越整函数且满足N(r,f)+N(r,1/f)=S(r,f),Ψ(z)形如
Ψ(z)=∑a(z)fl0(z)(f(z))l1…(f(k)(z))lk
为f(z)的微分多项式,且Ψ(z)中不含常数项.又设Ψ(z)的次数n>1,且满足l0 定理C设f(z)和Ψ(z)如定理B所述,且Ψ(z)的所有项中至少有两项具有不同次数,即Ψ(z)是非齐次的.则对所有的a≠∞,有δ(a,Ψ)<1-1/2n. 2011年,郑秀敏和陈宗煊在文献[6]中研究了差分多项式 (1) 的有限个差分乘积的和.其中I是指标λ=(λλ,0,λλ,1,…,λλ,n)的有限集,c1,c2,…,cn是不同的复常数.对P(z,f)的每一个单项式aλ(z)f(z)iλ,0f(z+c1)iλ,1f(z+c2)iλ,2…f(z+cn)iλ,n,记其次数为d(λ)=iλ,0+iλ,1+iλ,2+…+iλ,n.记P(z,f)的次数与下次数分别为 设d(P)≥1,得到了下面结论. 定理D设f(z)是有限级超越亚纯函数且满足N(r,f)+N(r,1/f)=S(r,f),又设P(z,f)为形如(1)式的差分多项式,其系数为f(z)的小函数,且P(z,f)中只有一个多项式具有最高次d(P).则 T(r,P(z,f))=d(p)T(r,f)+S(r,f). 定理E设f(z)是有限级超越亚纯函数且N(r,f)+N(r,1/f)=S(r,f),又设P(z,f)为形如(1)式的差分多项式,其系数为f(z)的小函数,P(z,f)中只有一个多项式具有最高次d(P).若d*(P)>0,则对任意的非零常数a,有 本文首先考虑差分多项式(1),得到了下述定理. 定理1设f(z)是有限级超越亚纯函数,且满足 N(r,f)=S(r,f), (2) 又设P(z,f)为形如(1)式的差分多项式,其系数函数和α(z)以及β(z)都为f(z)的小函数,且P(z,f)中只有一个单项式具有最高次d(P).则对任意的非零常数a,c,差分多项式 Q(z,f)=fn(z)(P(z,f)+α(z))+β(z)(fn(z+c)-fn(z))(n≥2) (3) 满足δ(a,Q(z,f))<1,从而Q(z,f)无穷多次取到任意有限非零复数. 进一步地,考虑微差分多项式 (4) 的有限个微差分乘积的和.其中I是指标λ=(λλ,0,λλ,1,…,λλ,n)的有限集,c1,c2,…,cn是不同的复常数.对P(z,f)的每一个单项式aλ(z)f(z)iλ,0(f′(z+c1))iλ,1(f″(z+c2))iλ,2…(f(n)(z+cn))iλ,n,记 定理2设f(z)是有限级超越亚纯函数,且满足 N(r,f)+N(r,1/f)=S(r,f), (5) 设P(z,f)为形如(4)式的微差分多项式,其系数是f(z)的小函数,且P(z,f)中只有一个多项式具有最高次d(P).若d*(P)>0,则对任意的非零有限常数a,有δ(a,P(z,f))≥d(P)/d*(P)-1. 引理1[8-9]设f(z)是非常数有限级亚纯函数,则等式 T(r+c,f)=T(r,f)+S(r,f),N(r+c,f)=N(r,f)+S(r,f) 对c>0成立,至多可能除去一个r的有限测度例外集. 在文献[8]结果的基础上,结合引理1可得到下面结论. 引理2设f(z)是非常数有限级亚纯函数,则m(r,f(z+c)/f(z))=S(r,f),其中c为复常数. 引理3[10]设f(z)为超越亚纯函数,k为任意正整数,则m(r,f(k)(z)/f(z))=S(r,f). 引理4设f(z)为超越亚纯函数,k为任意正整数,c为常数,则m(r,f(k)(z+c)/f(z))=S(r,f). 证明由引理2和引理3可得 即有m(r,f(k)(z+c)/f(z))=S(r,f). 定理1的证明采用反证法.假设存在某个非零常数a使得δ(a,Q(z,f))=1成立,记 F(z)=Q(z,f)-a, (6) 则 N(r,1/F)=N(r,1/(Q(z,f)-a))=S(r,Q(z,f)). (7) 由(1)式及引理1可知 (8) N(r,P(z,f))=S(r,f). (9) 由(3)和(8)式及已知条件可得 S(r,Q(z,f))=S(r,f), (10) 再由(7)和(10)式, N(r,1/F)=S(r,f). (11) 此外,由(2),(3),(6)和(10)式可得 N(r,F)=N(r,Q(z,f)-a)≤4nN(r,f)+N(r,P(z,f))=S(r,f). (12) 对(6)式两边同时求导得 F′(z)=fn-1(z)R(z,f), (13) 其中 显然,由(9)式可得N(r,P′(z,f))=S(r,f),进一步有 N(r,R(z,f))=S(r,f). (14) 因为f(z)是有限级超越亚纯函数,故由(6)和(9)式知F(z)也是有限级超越亚纯函数,从而由(11)与(12)式得 (15) 再由(13)—(15)式, (16) 一方面,显然有degQ(z,f)≥degP(z)+n>0.另一方面,由(2)和(16)式可知(4)式成立,从而定理E的条件成立.因此δ(a,Q(z,f))<1,这与假设矛盾.故对任意的非零常数a,差分多项式(3)满足δ(a,Q(z,f))<1,从而Q(z,f)无穷多次取到任意有限非零复数. (17) 其中 (18) 根据(4)—(5)式及引理1可知 (19) 故有d*(P)T(z,f)≤T(r,P(z,f))+S(r,P(z,f)).由d*(z)>0可知 (20) 再由(18)—(19)式可得 (21) 若a≠0,∞,则由(19)和(21)式以及第二基本定理可知 即有 (22) 由亏量的定义和(22)式有 即 [1] BHOOSNURMATH S S,KULKARNI M N,YU K W.On the value distribution of differential polynomials[J].Bull Korean Math Soc,2008,45(3):427-435. [2] CLUNIE J.On a result of Hayman[J].J London Math Soc,1967,42:389-392. [3] HAYKMAN W.Picard values of meromorphic functions and their derivatives[J].Ann Math,1959,71(1):9-42. [4] MILLOUX H.Les fonctions meromorphes et leurs derives[M].Paris:Hermann,1940:20. [5] YANG C C.On deficiecies of differential polynomials[J].Math Z,1970,116:197-204. [6] 郑秀敏,陈宗煊.某些差分多项式的亏量[J].数学学报,2011,54(6):983-992. [7] HALBURD R G,KORHONEN R J.Difference analogue of the lemma on the logarithmic derivative with applications to difference equations[J].J Math Anal Appl,2006,314:477-487. [8] HALBURD R G,KORHONEN R J.Finite-order meromorphic solutions and the discrete Painleve eqations[J].Proc London Math Soc,2007,94:443-474. [9] HAYMAN W K.Meromorphic Functions[M].Oxford:Oxford University Press,1964:28-86. [10] 金瑾,李里.关于亚纯函数φ(z)f(z)M[f]的值分布[J].华中师范大学学报(自然科学版),2015,49(4):483-487. [11] 金瑾.关于亚纯函数φ(z)f(z)(f(k)(z))nP[f]的值分布[J].应用数学,2013,26(3):499-505. [12] 金瑾.关于高阶线性微分方程解与其小函数的增长性[J].上海交通大学学报(自然科学版),2013,47(7):1155-1159. [13] 金瑾.关于一类高阶齐次线性微分方程解的增长性[J].中山大学报(自然科学版),2013,52(1):51-55. [14] 金瑾.一类高阶齐次数性微分方程解的增长性[J].华中师范大学报(自然科学版),2013,47(1):4-7. [15] 金瑾,樊艺,左建军,等.一类亚纯系数高阶非齐次线性微分方程解与小函数的增长性[J].上海大学学报(自然科学版),2014,20(6):726-732. [16] 金瑾.单位圆内高阶齐次线性微分方程解与小函数的关系[J].应用数学学报,2014,37(4):254-264. [17] 金瑾.高阶差分方程组的亚纯解[J].应用数学,2015,28(2):292-298. [18] 金瑾,武玲玲,樊艺.高阶非线性微分方程组的亚纯允许解[J].东北师大学报(自然科学版),2015,47(1):22-25. [19] 金瑾.高阶非线性代数微分方程组的可允许解[J].安徽师范大学学报(自然科学版),2014,37(2):114-119. Deficienciesofcomplexdifferencepolynomials JIN Jin1,2,ZHAO Hao-lan3 (1.Department of Mathematics,Guizhou University of Engineering Science,Bijie 551700,China; 2.Research Institute of Circular Economy,Guizhou University of Engineering Science,Bijie 551700,China; 3.School of International Economics and Trade,Shanghai Finance University,Shanghai 201209,China) Using the Nevanlinna theory of the value distribution of meromorphic functions,the problem of deficiency of difference polynomial is studied.Some results on deficiencies of difference polynomials of meromorphic functions of finite order are given,some of which can be viewed as difference analogues of corresponding results of difference polynomials,these results improve previous findings. difference polynomial;meromorphic function;finite order;deficiency 1000-1832(2017)04-0015-05 10.16163/j.cnki.22-1123/n.2017.04.004 2016-04-14 贵州省科学技术基金资助项目(2010GZ43286,2012GZ10526);贵州省毕节市科研基金资助项目(201102);贵州省教育厅自然科学重点项目([2015]392). 金瑾(1962—),男,教授,主要从事复分析研究. O 174.52学科代码110·34 A (责任编辑:李亚军)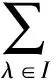
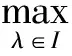
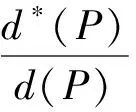
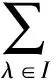
2 几个引理
3 定理的证明