基于协同相关度的作战任务分解优化
2017-12-19刘付显
王 伟,刘付显
(空军工程大学防空反导学院,西安 710051)
基于协同相关度的作战任务分解优化
王 伟,刘付显
(空军工程大学防空反导学院,西安 710051)
针对协同作战中任务分解的优化问题,构建了任务协同相关度的量化模型。对作战任务中几个基本概念进行定义,从时间、逻辑、功能3个维度对任务间的协同关系进行了形式化描述,在此基础上,建立了任务协同关系的综合度量模型。最后,通过设置任务协同度阈值的方法,对协同紧密的任务进行聚合,实现任务分解的优化。通过仿真实验验证了模型的可行性和有效性。
协同作战,任务分解,协同关系,量化模型
0 引言
现代战争的作战模式逐渐由以平台为中心的单一资源作战向以网络为中心的体系作战模式转变,诸军兵种协同的一体化联合作战将成为主要的作战样式。信息化条件下联合作战对军事组织间的有效协同提出了更高要求,体系作战能力的生成离不开协同。作战任务的分解是联合作战的关键问题之一,但由于作战任务之间存在复杂的协同关系,这就需要对作战任务之间的协同关系进行形式化描述和有效度量,为任务的合理分解提供依据。
目前,对任务协同关系的研究主要集中在定性层面[1-5],还存在对协同关系描述不够全面、量化不足等问题。本文从时间、逻辑和功能3个角度对作战任务之间协同关系进行描述,并建立任务之间协同强度的量化模型,将协同度较高的任务进行耦合,实现任务分解的优化。
1 作战任务描述
协同作战的顺利实施需要作战任务的统一规范化表达,以利于各参战力量清晰地理解整个作战任务的内涵,明确各作战子任务的协同关系。
定义1[6]作战任务是作战力量在一定的战场态势下,为达成预定作战目的,而采取的一系列相互关联行动的有序集合。
将作战任务形式化为以下四元组:
式中,Name为任务名称;Target为任务的目标;Time=<T_Start,T_End> 为任务执行时间,T_Start为任务开始时间,T_End为任务结束时间,任务结束时间为T_Dur=T_End-T_Start;Relation为任务的关系,包括任务间的纵向关系和横向关系。
定义2 原子任务是不可再分的任务,仅包含一个行动,可以直接执行。
定义3 复合任务是由个若干相关的原子任务组成的复杂任务集合。
2 作战任务协同关系描述
2.1 作战任务协同时间关系
在协同作战过程中,各作战任务的执行时间存在先后次序,作战协同表现为任务间的时间关系。根据Allen区间代数的定义[7],作战任务的协同时间关系共有7种,如表1所示。

表1 作战任务协同时间关系
2.2 作战任务协同逻辑关系
各作战任务紧密相关、环环相扣,某一作战任务的成败将会影响其他任务的执行,作战协同表现为任务间的逻辑关系,如图1所示。
2.2.1 顺序关系
对于ti,tj∈T,若有sequence(ti,tj),表示当任务ti成功执行后,任务tj才能开始执行。
2.2.2 与—与关系
2.2.3 与—或关系
2.2.4 或—与关系
2.2.5 或—或关系
2.3 作战任务协同功能关系
各作战任务相互支撑、相互配合,作战协同表现为任务间的功能关系,如图2所示。
2.3.1 依赖关系
对于任务ti,tj∈T,若tj需要依靠ti输出的信息才能执行,则tj对ti具有信息依赖关系,表示为infor_dependent(ti,tj);若tj需要依靠ti达成的效果才能执行,则tj对ti具有效果依赖关系,表示为effect_dependent(ti,tj);若tj需要依靠ti信息和效果才能执行,则tj对ti具有完全依赖关系,表示为dependent(ti,tj)。若ti和tj为并行关系,则为并行依赖;若ti和tj为串行关系,则为串行依赖。
2.3.2 耦合关系
对于任务ti,tj∈T,若ti和tj需要依靠彼此输出的信息才能执行,则ti和tj具有信息耦合关系,表示为infor_couple(ti,tj);若ti和tj需要依靠彼此达成的效果才能执行,则ti和tj具有效果耦合关系,表示为effect_couple(ti,tj);若ti和tj需要依靠彼此的信息和效果才能执行,则ti和tj具有完全耦合关系,表示为couple(ti,tj)。
2.3.3 独立关系
对于任务ti,tj∈T,若ti和tj不需要依靠彼此输出的信息或效果就能执行,则ti和tj具有独立关系,表示为independent(ti,tj)。
3 作战任务协同度量化分析
各作战任务由于存在时间、逻辑和功能上的关系,必然存在一定的相关性,任务间相关性的准确度量对任务分解优化和分配具有重要作用,下面从3个维度量化分析任务的协同相关度。
3.1 时间协同度量
(1)假设任务 ti和 tj的时间协同关系为Meets(ti,tj),其时间协同相关度为α。
(2)假设任务 ti和 tj的时间协同关系为Before(ti,d,tj),其时间协同相关度为。
(3)假设任务ti和tj的时间协同关系为Overlaps(ti,tj),其时间协同相关度为。
(4)假设任务ti和tj的时间协同关系为During(ti,tj),Starts(ti,tj),Finishes(ti,tj),Equal(ti,tj),其时间协同相关度为。
3.2 逻辑协同度量
(1)假设任务ti和tj的逻辑协同关系为Sequence(ti,tj),其逻辑协同相关度为RLij=1。
(2)假设T1和T2的逻辑协同关系为And_And(ti,tj),则T1中某一任务t1i与T2中某一任务t2k的逻辑协同相关度为RLik=1/(mn),T1中任务之间的逻辑协同相关度为RLij=1/n,T1中任务之间的逻辑协同相关度为RLkl=1/m。
(3)假设T1和T2的逻辑协同关系为And_Or(ti,tj),则T1中某一任务t1i与T2中某一任务t2k的逻辑协同相关度为RLik=1/(mn),T1中任务之间的逻辑协同相关度为RLij=1/n,T1中任务之间的逻辑协同相关度为RLkl=0。
(4)假设 T1和 T2的逻辑协同关系为Or_And(ti,tj),则T1中某一任务t1i与T2中某一任务t2k的逻辑协同相关度为RLik=1/(mn),T1中任务之间的逻辑协同相关度为RLij=0,T1中任务之间的逻辑协同相关度为RLkl=1/m。
(5)假设 T1和 T2的逻辑协同关系为Or_Or(ti,tj),则T1中某一任务t1i与T2中某一任务t2k的逻辑协同相关度为RLik=1/(mn),T1中任务之间的逻辑协同相关度为RLij=0,T1中任务之间的逻辑协同相关度为RLkl=0。
3.3 功能协同度量
(1)假设任务ti和tj的功能协同关系为indepen dent(ti,tj),其功能协同相关度为RLij=0。
(2)假设任务ti和tj的功能协同关系为dependent(ti,tj),其功能协同相关度采用1~9级标度量化,如表2所示。
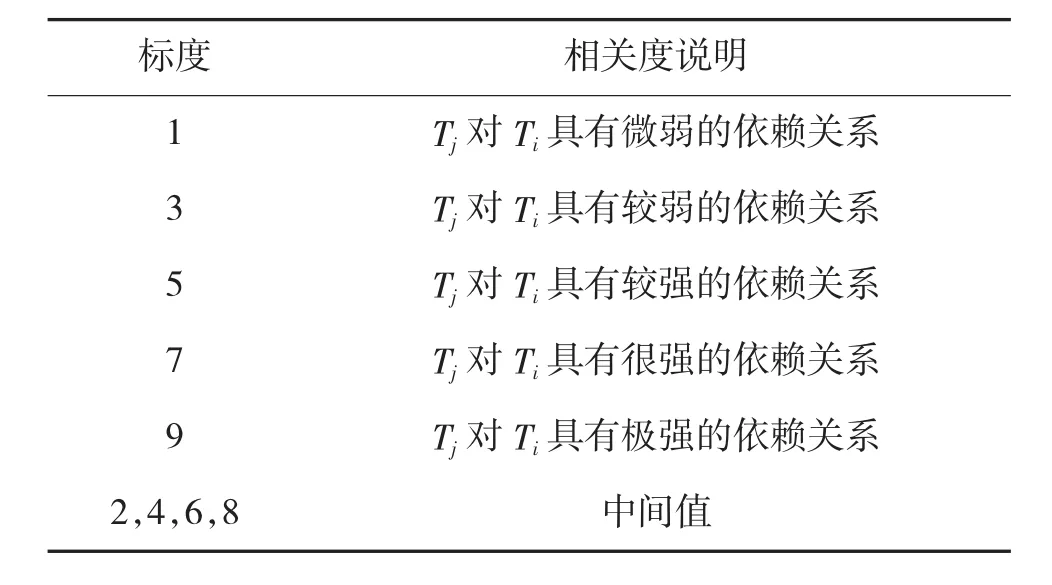
表2 功能协同相关度标度
(3)假设任务ti和tj的功能协同关系为couple(ti,tj),其功能协同相关度采用1~9级标度量化,但由于耦合关系中ti和tj互相依赖,所以其相关度值RLij=标度值×2。
3.4 综合协同度量
综合协同相关度反映了综合考虑各种因素下任务之间的协同相关程度,其值Rij由时间协同相关度RTij、逻辑相关度RLij和功能相关度RFij表示
3.5 基于协同度的任务分解优化
构造任务相关矩阵R描述任务之间的协同度,R为N×N阶方阵,N为任务数量,矩阵的行和列对应不同的任务,矩阵对角线元素Rii=0,其他元素为Rij。
在任务分解时,可以通过设置协同相关度阈值λ,对任务分解粒度进行优化。
当Rij≤λ时,任务ti和tj可以分解成两个独立的任务分别进行处理。
当Rij>λ时,说明任务ti和tj之间存在较大的协同相关性,应该将其合并为一个任务来处理,或者将这两个任务分配给协同效能较高的资源进行处理。
相关度阈值λ应该根据任务所处的层次来确定。对于高层次的任务,由于各子任务本身的任务量较大,各子任务应该尽量能够独立执行,因此,λ的值应取得较大;对于低层次的任务,λ的值可以逐步减小,使更多的具有高度协同相关性的任务能够联合执行,提高协同效能。
4 案例分析
下面以协同登岛作战为例[8],对基于协同关系的作战任务分解优化方法进行说明。作战总目标是夺取港口,港口南侧有一处适宜登陆的海滩,海滩和港口之间有公路相连。在登陆海滩之前,有一个高地首先需要控制。协同度阈值λ=6。想定的战场态势图如图3所示。
根据战场态势对占领港口的任务进行分解,作战任务之间的关系如图4所示。
具体任务为:t1占领高地 Time=<0,10>,t2占领海滩 Time=<10,20>,t3清除地雷 Time=<20,25>,t4公路行进 Time=<25,40>,t5切断桥梁 Time=<30,40>,t6北 区 防 御 Time=<25,40>,t7占 领 海 港Time=<40,50>。
子任务间协同关系如表3所示。

表3 子任务间协同关系
各子任务的综合协同相关度为
由综合协同相关度矩阵R可知,子任务t3和t4的相关度为8>λ。因此,在任务分配时应该将t3和t4合并为一个任务来处理,或者将这两个任务分配给协同效能较高的平台资源执行。
5 结论
本文针对协同作战中任务分解的优化问题,构建了基于任务协同相关度的分解优化方法。首先对作战任务中几个基本概念进行定义,然后对7种时间协同关系、5种逻辑协同关系、3种功能协同关系进行了形式化描述,在此基础上,建立了任务协同关系的综合量化模型。最后,通过设置任务协同度阈值的方法,对协同紧密的任务进行聚合,实现任务分解的优化。
[1]程恺,车军辉,张宏军,等.作战任务的形式化描述及其过程表示方法 [J].指挥控制与仿真,2012,34(1):15-19.
[2]张万鹏,王楠,陈璟.一种利用工作流模型的分层任务网络规划领域建模方法[J].智能系统学报,2011,6(3):239-247.
[3]李建国,汤庸,黄世平,等.基于任务依赖关系的群体感知模型[J].东南大学学报(自然科学版),2011,41(2):290-295.
[4]鲁法明,曾庆田,包云霞,等.基于流程案例簇的任务关系挖掘算法[J].计算机集成制造系统,2013,19(8):1771-1783.
[5]王景峰,王刚.制造服务逻辑关系确定方法研究[J].计算机工程与应用,2012,46(2):197-199.
[6]李建军,刘翔,任彦,等.作战任务高层本体描述及规划[J].火力与指挥控制,2008,33(1):53-55.
[7]ALLEN J F.Maintaining knowledge about temporal intervals[J].CommunicationsoftheACM, 1983, 26(11):823-843.
[8]LEVCHUK G M,LEVCHUK Y N,LUO J.Normative design of organizations—part I: mission planning [J].IEEE Transactions on Systems,Man,and Cyberneetics,2002,32(3):346-359.
Operation Task Decomposition Optimization Based on Cooperative Correlation Degree
WANG Wei,LIU Fu-xian
(School of Air and Missile Defense,Air Force Engineering University,Xi’an 710051,China)
For the problem of task decomposition optimization in cooperative operations, a quantitative model about cooperative correlation degree between tasks is proposed.Several basic concepts are defined,the cooperative relation is described from time dimension,logic dimension and function dimension respectively.Then the integrated quantitative model is established.Finally the tightly cooperative tasks are integrated to optimize the task decomposition by setting threshold value of cooperative correlation degree.Example is provided to demonstrate the feasibility and effectiveness of the proposed model.
cooperative combat,task decomposition,cooperative relation,quantitative model
E917
A
10.3969/j.issn.1002-0640.2017.11.23
1002-0640(2017)11-0107-04
2016-09-23
2016-11-17
王 伟(1988- ),男,山东日照人,博士研究生。研究方向:指挥决策分析。
