基于多群体改进萤火虫算法的装配序列规划

张 琦，程培源，程月蒙

（空军工程大学防空反导学院，西安 710051）

基于多群体改进萤火虫算法的装配序列规划

张 琦，程培源，程月蒙

（空军工程大学防空反导学院，西安 710051）

为了解决机械产品装配序列优化问题，提出了一种基于多群体改进萤火虫优化算法的装配序列规划方法。建立了装配序列规划的数学模型，针对萤火虫算法收敛效率低的不足，借鉴混合蛙跳算法族群划分思想对萤火虫算法进行了改进，引用局部搜索与全局信息交换机制提升了算法性能；根据装配序列规划问题离散型的特点，定义了新的离散编码方式和粒子更新策略。通过实例仿真结果表明，改进后的萤火虫优化算法简单有效、稳定性好、求解精度高，能够稳定快速地给出装配序列最优方案。

装配序列，萤火虫优化算法，混合蛙跳算法

0 引言

装配序列规划（Assembly Sequence Planning，ASP）是针对机械产品的装配环节，进行最优序列的选取，旨在提高装配体装配效率，ASP问题实质上是一个典型组合优化问题。其本身就具有离散性、强约束、复杂性和多样性的特点［1］。

传统的解决方法仅仅满足于零件数量少的简单装配问题，效率不高。随着智能算法的不断改进优化，在解决组合优化问题中呈现出良好效果和巨大潜力，因而有学者提出将智能算法应用在解决装配序列规划问题上。诸如遗传算法［2］、免疫算法［3］、蚁群算法［4］、粒子群算法［5］、蛙跳算法［6］等等各种智能优化算法。但现有文献应用智能算法在求解和优化ASP问题时，仍存在着一些困难：如何克服组合爆炸问题［7］；如何对算法的性能进行改进；如何建立简单有效的ASP数学模型选择最优装配序列等仍是研究的难点和热点。

萤火虫优化算法（Glowworm Swarm Optimization，GSO）［8］是一种新型智能优化算法，在解决大量实际优化问题过程中，展现出了良好的性能。已有学者应用萤火虫算法验证了在求解各种组合优化问题和NP难度问题上的可行性和有效性［9］，为解决ASP问题提供了新思路，进而把萤火虫算法扩展到解决装配序列规划问题中来。

1 ASP可行性序列及数学模型

1.1 装配可行性分析

在子装配体上装配零件时，必须先考虑装配零件的装配可行性，可以利用集成干涉矩阵获取零件的装配信息，继而判断序列是否具有装配可行性。

设某装配体由 n 个零件{P1，P2，…，Pn}组成，A=（Iijx，Iijy，Iijz）n×n表示装配干涉矩阵，元素Iijx表示零件Pi沿+x方向装配与零件Pj的干涉情况。

且根据干涉矩阵的特点，沿负方向-x装配时，得出I+ijx=I-jix，其他方向依次类推。

设 S=（P1，P2，…，Pi-1）为未完成装配的一个零件序列，则待装配零件Pi的几何可行性由式（2）判定

D表示笛卡尔坐标系的6个轴向方向，若式（2）为0，则表示零件沿该方向装配可行；若式（2）不为0，则发生干涉，此装配序列不可行。

1.2 适应度函数的构造

复杂机械产品的装配序列优化通常以降低装配难度、提高装配效率和节约成本为最终目标，然而为精确实现目标，涉及的参数很多。

本文通过对装配操作过程中关键因素的分析，结合机械装配设计和生产的要求，选取了其中权重系数较大的几个参数作为评价指标，其中包括装配稳定性、装配聚合性和装配重定向性，并详细量化了各项指标的计算方法，最终通过加权方式确定其适应度函数，为最优可行装配序列的选择提供了数学基础。

1.2.1 稳定性

装配稳定性是指每一操作步骤涉及的零部件在重力及建立装配所需外力的作用下，装配体保持内部稳定关系的能力总和。稳定关系采用连接矩阵C=（Cij）n×n和支撑矩阵S=（Sij）n×n来表示。元素Cij和元素Sij分别表示零件Pi与零件Pj之间的连接类型、支撑关系。f1表示不稳定操作出现次数。

1.2.2 装配的聚合性

聚合性代表装配过程中装配工具及辅助用具的变化次数，不同零件涉及的操作工具也不尽相同，多次更换工具导致装配效率的降低。因此，减少装配工具的更换，增强操作的聚合性才能满足装配需求。用f2表示装配工具的改变次数。

1.2.3 装配的重定向性

装配的重定向性表示装配方向的变化次数，次数变化越少，可避免频繁换向操作，装配效率也极大提高。f3表示装配方向的改变次数。

基于易存储、表达和快速计算的目的，对零件基本特征信息以及零件间的装配关系信息进行梳理，利用干涉矩阵、连接矩阵、支撑矩阵以及工具矩阵表征零件装配信息［10］，其内部关系如图1所示。

以上可看出，上述评价装配成本的包含两大要素：几何约束和工艺约束，前者可剔除无效装配序列，压缩解空间大小；后者则包括装配工具、装配连接类型等工艺信息，在实际操作中，对装配成本的影响较大。

1.2.4 适应度函数

根据上述装配成本的分析，定义ASP问题的适应度函数如下：

其中 ω1、ω2、ω3分别是稳定性、聚合性、重定向性各考查指标的权重，为0～1之间的实数，并且ω1+ω2+ω3=1。基于各因素的重要程度，取ω1=0.4，ω2=0.35，ω3=0.25。根据装配序列评价函数可知，在各评价指标权重系数不变的情况下，装配序列评价函数值（适应度函数）越小，表示装配成本越小，装配序列越好。

2 萤火虫优化算法

GSO算法起源于对自然界中萤火虫的求偶或觅食过程的模拟，由印度学者Krishnanand和Ghose于2005年最先提出［11］。其仿生原理是：一定区域内的萤火虫种群，其个体的吸引、移动行为类比为算法搜索、优化过程，萤火虫亮度度量成求解问题的目标函数，亮度大的个体吸引邻域内其他个体，最终聚集到最亮的萤火虫周围。

2.1 基本萤火虫算法

在GSO算法中，每个萤火虫代表问题的一个可行解，解的适应度表征为该萤火虫的亮度（萤光素）。每次迭代开始，萤火虫个体在其感知范围内搜索比自身亮的个体构建邻域集，并以轮盘赌的方式随机向其移动。在所有萤火虫移动完毕后，依据自身邻域集的大小更新各自感知半径，同时更新亮度进入下一轮迭代。通过多次迭代，萤火虫将聚集在多个较亮个体的周围。具体算法模型［11］如下：

Step 1 在解空间内任意设定m∈N个可行解x1，x2，…，xm

Step 2 萤光素更新阶段

萤火虫xk在第t次迭代更新的亮度为lk（t）

ρ∈（0，1）为萤光素挥发因子，γ∈（0，1）为萤光素更新率，f（xk）表示xk的目标函数。

Step 3在其动态感知半径rk（t）内，萤火虫选择比自己亮度大的个体建立邻域集Nk（t）。

‖·‖表示欧氏距离，rk表示萤火虫xk的感知半径。

Step 4 位置更新阶段

萤火虫xk通过式（11）所得概率pkj以轮盘赌的方式向萤火虫xj移动，式（12）为移动公式，s为移动步长。

Step 5 感知范围更新

第t次迭代，萤火虫的感知半径更新为

γs为最大感知半径，β为感知范围更新系数，Nt为邻域集所包含萤火虫数目的阈值，表示集合所包含的元素个数。

Step 6 判断算法是否达到设定的迭代次数或当前最优解符合期望，满足终止条件则结束。否则，返回执行Step 2。

以上可以看出算法概念简单，流程清晰，参数的设置也比较简单，没有交叉和变异等复杂的操作，因此，更加易于理解、实现和操作。

为了克服GSO收敛精度低、易陷入局部最优的缺陷，本文结合混合蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）［12］族群划分思想，将萤火虫群体均分为等规模的子族群，个体在参与整个种群信息交流之前须在子族群中进行局部搜索，因而采用局部迭代和全局信息交换的方式可提高GSO收敛效率。

均分方法为：将萤火虫所有个体的适应度f［Xk（t）］按照数值降序排列，然后各个族群均分获得等规模的个体，每个族群得到的萤火虫数量为Q，其中Ei代表第i个族群（如图2所示），则：

2.2 混合蛙跳算法（SFLA）

SFLA集聚粒子群算法和元算法Memetic的优点。是一种基于群体智能的新型优化算法［13］。SFLA算法原理：初始化随机产生F只青蛙群体Pt={X1（t），…，Xk（t），…，XF（t）}，k=1，2，…，F，计算个体的适应度f［Xk（t）］。开始迭代过程，适应度按照大小降序进行排列，并均分到M个族群中，每个族群中N只青蛙，则F=M×N。

在得到每个族群函数适应度值的基础上，SFLA对每个最劣解Xω（t）按式（15）更新：

式（15）中：r∈［0，1］为随机系数，Xb（t）为族群中最优解，Xg（t）为蛙群体中最优解。

如果新解Xnew（t）适应度优于Xω（t），则更新最差解Xω（t+1）=Xω（new）；否则Xg（t）代替Xb（t）重新执行更新策略式（14），若新解Xnew（t）适应度优于Xω（t），则更新Xω（t+1）=Xω（new）；否则，产生一个随机解替换Xω（t）。所有以上方式挨个对族群重复迭代进行局部搜索，完成最差位置个体的更新。然后各个族群青蛙重新混合排序，再次将族群划分进行局部搜索，直至达到终止条件结束算法迭代。

2.3 基于多群体改进萤火虫算法的改进策略

虽然萤火虫优化算法是一种比较新颖的优化算法，其性能也在解决许多实际优化问题中得到较好的体现，但难以避免基于群体搜索的随机优化算法所具有的通病和缺陷。针对算法的不足结合实际问题提出以下两点改进：

1）GSO算法实现把萤火虫个体亮度值相互交流限制在了领域集空间，将所有个体划分为若干聚集区域，避免了陷入局部最优的风险，但是区域内亮度较大的个体无法实现夸域交流，使得个体最优信息无法传递，收敛速度降低；

2）SFLA算法在运行后期容易出现收敛速度变慢、早熟收敛以及陷于局部最优，从而引起求解精度低等问题。

为了改善两算法的性能，达到求解的目的，提出将SFLA与GSO算法融合，种群均分成规模等同的两个种群，各个种群首先分别独立执行各自搜索，每次迭代结束后交流最优信息（具体步骤在第4节说明）。种群之间交流并相互借鉴并保留最优信息，实现了多种群协同进化，提升了GSO跳出局部最优能力。

3）GSO与SFLA算法主要解决连续函数优化问题，而ASP属于离散优化问题［14］，因此，需要重新设计基本萤火虫优化算法的框架，定义新的离散编码方式。

定义多群体改进GSO算法的粒子编码方式为Xk（t）=（xk1，xk2，…，xkn）T，其中xkl∈［0，m］，Xk（t）∩［0，m］≠φ

4）对于离散型萤火虫编码方式，如果沿用式（12）、式（15）更新，得到的解显然不符合要求，算法的求解速度，基于此提出以下新的离散编码的粒子更新策略：

3 算法流程

1）相关参数和系数设置；

2）设定最大循环次数 Tmax，Tmin

3）随机生成萤火虫初始群体，并均分成等规模GSO群体和SFLA群体；

4）计算各自群体中个体的适应度值f［XkGSO（t）］和f［XkSFLA（t）］；

5）根据式（14）和式（15）分别对两种群进行种群划分；

6）GSO 种群内萤火虫根据式（9，13，16，17）更新；

7）i=i+1

8）SFLA 种群内青蛙根据式（16）、式（17）更新；

9）l=l+1

10）比较f［XkGSO（t）］与f［XkSFLA（t）］两者的大小，若f［XGSO（t）］≤f［XSFLA（t）］，则用XGSO（t）代替XSFLA（t）来引导青蛙的进化方向；否则用XSFLA（t）代替XGSO（t）来引导萤火虫的进化方向。

11）根据式（15）更新全局最优解Xbest（t）；

12）t=t+1

}

程序结束，输出全局最优解。

4 实例验证

以基座的装配为例，进行算法验证

5 结果分析

5.1 实验设置

5.1.1 实验环境

文章涉及的算法代码采用Matlab R2013a编写，仿真运行的计算机参数：32位Windows7操作系统 Intel（R）Core （TM）i3-3240 CPU@3.40 GHz 4.00GB内存。

5.1.2 参数设置

根据Krishanand和Ghose对GSO参数的对比分析，参数取值如下［11］：ρ=0.4，γ=0.6，β=0.08，nt=5，s=0.03，l0=5，迭代次数 200 次，种群数 100。

5.2 运行结果

经过多次实验测试以及结合图3、图4干涉矩阵，工具集合进行分析，随着迭代次数的增加平均适应度函数值不断下降，如图5所示，第15代稳定在最优适应度值1.3。适应度值对应的装配序列结果为：

经分析，上述装配序列符合装配要求，满足工程应用的需求。

表1 零件装配工具集合

表2 集成干涉矩阵

5.3 分析对比

5.3.1 不同种群容量下的迭代结果

在不同种群容量下对算法进行实验，迭代次数为50次实验结果如下页图6所示。

从图6可以看出，当种群容量为50时取得全局最优适应度1.3的次数为9；种群容量为100时，次数增加到19次。并且随着种群容量的增加，50次局部最优适应度的平均值会减小，说明种群容量的大小对算法的求优质量影响较为明显。

种群容量对算法的求解效果有显著影响，随着种群容量增加，个体多样性越明显且越容易收敛到全局最优，但算法运行耗时也长，种群容量越小，越易陷入局部最优［15］。

5.3.2 算法对比

a.基于同样的适应度函数以及程序运行环境（种群容量为100时，200次试验）两种算法平均适应度的变化情况如图7所示。

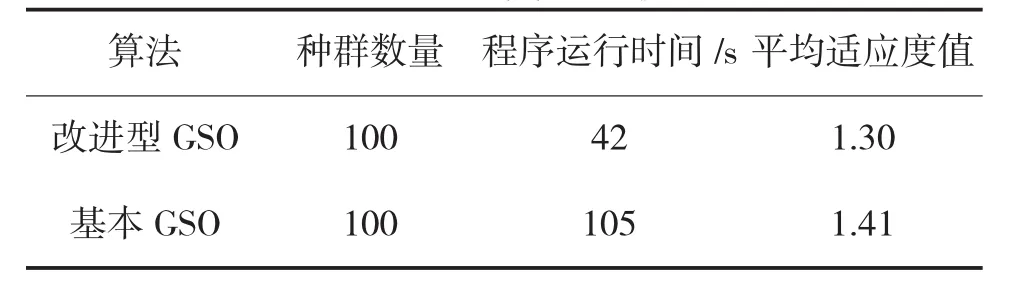
表3 运行结果比较

可以看出，融合改进型GSO算法在第81代就趋于收敛，而基本GSO在第110代收敛到最优解，改进后的GSO算法相比较收敛速度快；并且基本GSO算法易陷入局部收敛。因而，融合改进型GSO算法比基本GSO算法的质量、性能和效率均有显著的提升。

b.将本文算法分别与同类解决ASP问题的文献［16-18］算法进行进一步对比，文献［16］提出人工萤火虫结合模拟退火（SA，Simulated Annealing）的离散SA-GSO算法，文献［18］提出的改进萤火虫的FA算法（FA，Firefly Algorithm）。由图 8可知，本文改进算法的收敛速度均优于后两者文献的算法，而且最优适应度值在也略优于后两者。其实验结果对比如表4所示，得到本文算法的最优适应度值相比最小、最好。由此可见，在机械产品的装配序列规划问题中，本文的算法性能和效率都优于后两文献的算法。

6 结论

本文针对ASP问题特点，在基本萤火虫算法的基础上，提出一种基于多群体改进萤火虫算法的装配序列规划研究。首先建立了装配序列规划的数学模型，针对萤火虫算法收敛效率低的不足，借鉴混合蛙跳算法族群划分思想对萤火虫算法进行了改进，引用局部搜索与全局信息交换机制提升了算法性能；接着根据装配序列规划问题离散型的特点，定义了新的离散编码方式和粒子更新策略，本文的研究结果表明基于多群体改进萤火虫算法的装配序列规划方法是一种行之有效的方法，达到了提高萤火虫算法的寻优能力的目的。

表4 3种算法实验结果

［1］梁丽芬.基于自适应混沌粒子群算法的装配序列规划研究［D］.太原：中北大学，2016.

［2］杨威，孟冠军，曹文钢，等.基于改进遗传算法的装配序列优化［J］.机械传动，2016，40（9）：67-70.

［3］苏强，吴海龙，赖盛杰.基于免疫遗传算法的装配顺序优化 ［J］. 同济大学学报 （自然科学版），2015，43（6）：944-950.

［4］徐周波，肖鹏，古天龙，等.基于混沌混合算法的装配序列规划［J］.计算机集成制造系统，2015，21（12）：3200-3207.

［5］于宏，王成恩，于嘉鹏，等.基于粒子群算法的复杂产品装配序列规划［J］.东北大学学报（自然科学版），2010，31（2）：261-264.

［6］王松，孙振忠，郭建文，等.基于混合蛙跳算法的复杂产品装配序列规划［J］.计算机集成制造系统，2014，20（12）：2991-2999.

［7］WANG Y，LIU J H，LI L S.Assembly sequence merging based on assembly unit partitioning ［J］.Int.J.Adv.Manuf.Technol，2009，45（1）：808-820.

［8］KRISHNANAND K N，GHOSE D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics［C］//Proc of the IEEE Swarm Intelligence Symposium.Pasadena，USA，2005：84-91.

［9］周永权，黄正新.求解TSP的人工萤火虫群优化算法［J］.控制与决策，2012，27（12）：1816-1821.

［10］敬石开，李连升，曾森，等.面向产品装配序列规划的智能优化算法库［J］.计算机辅助设计与图形学学报，2010，22（9）：1593-1599.

［11］KRISHNANAND K N，GHOSE D.Glowworm swarm optimization：a new method for optimizing multimodal functions［J］.International Journal of Computational Intelligence Studies，2009，25（1）：93-119.

［12］肖莹莹，林廷宇，李伯虎，等.混合蛙跳算法自适应参数调整改进策略［J］.系统工程与电子技术，2016，38（8）：1939-1950.

［13］DEEP K，BANSAL J C.Mean particle swarm optimization for function optimization［J］.International Journal of Computational Intelligence Studies，2009，25（1）：72-92.

［14］倪志伟，梁婷，伍章俊，等.面向数据中心虚拟机部署的智能优化策略［J］.模式识别与人工智能，2015，28（4）：306-308.

［15］吴宏超，刘检华，唐承统，等.基于萤火虫算法的管路系统布局序列优化技术［J］.计算机集成制造系统，2016，22（8）：1843-1844.

［16］陆屹，程培源，齐悦，等.基于改进人工萤火虫算法的装配序列规划研究［J］.测控技术，2016，35（3）：140-144.

［17］曾冰，李明富，张翼，等.基于萤火虫算法的装配序列规划研究［J］.机械工程学报，2013，49（11）：177-184.

［18］曾冰，李明富，张翼.基于改进萤火虫算法的装配序列规划研究［J］.计算机集成制造系统，2014，20（4）：799-806.

Assembly Sequence Planning Based on Multi-Intelligence Improved Glowworm Swarm Optimization Algorithm

ZHANG Qi，CHENG Pei-yuan，CHENG Yue-meng
（School of Air and Missile Defense，Air force Engineering University，Xi’an 710051，China）

In order to solve the problem of assembly sequence optimization of mechanical products，a new assembly sequence planning method based on multi group improved glowworm swarm optimization is proposed.Firstly，the mathematical model of assembly sequence planning is established.Aiming at the shortage of glowworm swarm optimization convergence efficiency，using SFLA population division thought improved the firefly algorithm，citing local search and global information exchange mechanism to enhance the performance of the algorithm.Then according to the characteristics of the discrete assembly sequence planning problem，the definition of discrete encoding and new particle update strategy.Finally，the simulation results show that the improved algorithm is simple and effective，the stability is better.

assembly sequence planning，glowworm swarm optimization，shuffled frog leaping algorithm

TP391

A

10.3969/j.issn.1002-0640.2017.11.21

1002-0640（2017）11-0097-06

2016-09-08

2016-11-09

张 琦（1993- ），男，陕西西安人，硕士研究生。研究方向：军用电力系统及其自动化。