基于Kronecker积的分形图案设计及在望江挑花中的应用

袁惠芬， 程皖豫， 王 旭， ， 刘新华，

(安徽工程大学 a． 纺织服装学院； b． 纺织行业科技公共服务平台， 安徽 芜湖 241000)

基于Kronecker积的分形图案设计及在望江挑花中的应用

袁惠芬a， 程皖豫b， 王 旭a， b， 刘新华a， b

(安徽工程大学 a． 纺织服装学院； b． 纺织行业科技公共服务平台， 安徽 芜湖 241000)

为了丰富望江挑花图案设计，提出一种基于矩阵Kronecker积的分形图案生成方法，并将其应用于望江挑花图案设计．在建立图案布尔矩阵模型的基础上，运用Kronecker积实现了基础图案矩阵的多级分形处理，结合基础图案矩阵的反矩阵和填充图案矩阵的多级分形处理，并相互叠加生成分形图案矩阵．研究结果表明，运用矩阵Kronecker积可快速实现图案矩阵的多级分形处理．结合矩阵叠加处理，随基础图案、填充图案矩阵的不同，可生成各具特色的多级分形图案．该方法拓宽了望江挑花图案设计的思路．

望江挑花； Kronecker积； 分形； 布尔矩阵

传承千年的望江挑花是源于安徽望江的汉族传统手工刺绣，其作为装饰纺织品分别于1979、1982和2000年三度进入人民大会堂安徽厅[1-2]，并于2008年入选国家级非物质文化遗产．图案设计是望江挑花加工过程中的重要环节．和其他民间手工刺绣一样，望江挑花图案题材以民俗为主，图案以象形、寓意见长，如牡丹寓“富贵”、蝙蝠寓“福”、鹿寓“禄”等，充满浓郁的民俗气息．传统的望江挑花图案由挑花艺人手工绘制，工作量大，易出错，且效率低，图案元素虽然多样，但主题相对单一，缺乏时尚性和现代感．如何运用计算机辅助图案设计、丰富望江挑花图案的多样性和时尚感，成为提高设计质量、效率及开拓应用市场的关键环节．随着分形艺术在纺织品设计领域应用的日益广泛，运用计算机生成分形图案逐渐受到研究者的重视，其中矩阵Kronecker积是织物组织设计及分形图案设计的有效方法之一．文献[3]运用Kronecker积研究了自身接结、空心袋、表里换层等双层组织的设计方法．文献[4]运用Kronecker积实现了组织嵌入、组织点加强及组织点置换等变化绉组织设计．文献[5]运用L系统分形原理，生成具有4级自相似结构的平纹分形组织，并讨论了其与填充组织配合应用于提花组织图案设计．文献[6]利用Kronecker积生成了各种具有精细的自相似结构的分形图，与L系统和迭代函数系统的分形图案相比，其自相似结构更为复杂，且图像缩放易于实现．文献[7]运用Kronecker积生成具有自相似结构的编织图案．目前，Kronecker积在纺织图案设计的研究主要集中在织物组织、提花图案或编织图案设计方面，而基于Kronecker积的分形图案应用于望江挑花图案设计的研究尚未见报道．

本文通过矩阵Kronecker积的方法，将基础图案矩阵及其反矩阵的多级分形矩阵或填充组织矩阵，采用叠加的方式生成分形图案并将其应用在望江挑花作品上．研究结果表明，通过基础图案及填充组织的变化，可生成的各具特色的分形图案，对丰富望江挑花图案设计及开发新产品具有一定的参考价值．

1 矩阵Kronecker积在分形中的应用

1．1 矩阵Kronecker积

Kronecker积是矩阵的一种运算方法．令矩阵C是矩阵A和B的Kronecker积，若A为m×n矩阵，而B为p×q矩阵，则C为mp×nq矩阵，计算过程如下：

C=A⊗B=

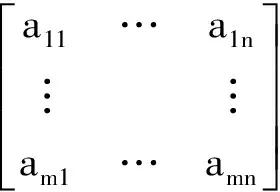
1．2 Kronecker积在分形中的应用

由Kronecker积的定义，A⊗B等价于将矩阵B嵌入矩阵A中1元素所在的位置，而矩阵A中0元素所在的位置将用与矩阵B同维的全0元素矩阵替代．继续迭代计算则生成阶数更高、具有更精细自相似结构的多级分形图案．基础图案可用3×3的布尔矩阵A表示，如图1(a)所示．

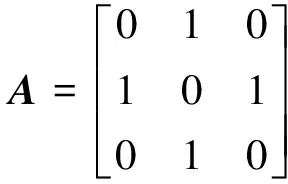
当A=B时，经Kronecker积运算，即A⊗A，则生成如图1(b)所示的一级分形图案，继续迭代则产生图1(c)所示的二级分形图案．

(a) 基础图案 (b) 一级分形图案

(c) 二级分形图案 图1 基于Kronecker积的分形图案示意图Fig．1 The sketch map of fractal pattern based on Kronecker product

1．3 基于Kronecker积的分形图案生成

望江挑花的图案由针迹单元组合形成[7]，若将图案用布尔矩阵表示，即图案的针迹单元部分用元素1表示，图案的空白部分用元素0表示．由图1所示，直接通过矩阵Kronecker积，可形成具有自相似结构特征的分形图案，但基础图案经过多级分形后图案面积迅速增加，且存在图案稀疏的情况，不适合直接用于望江挑花图案．研究发现，通过对基础图案矩阵进行Kronecker积分形，并结合矩阵叠加的方式，可设计出具有分形效果且符合要求的望江挑花图案．叠加方式包括两种：一种是分别将基础图案矩阵及其反矩阵(1、 0元素互换)经过分形后叠加；另一种是将基础图案矩阵经过分形后与填充组织叠加．为加快分形图案矩阵的生成过程，可采用计算机程序进行相关运算，考虑到矩阵运算的优势，本文采用Matlab程序，其生成的程序流程如图2所示．

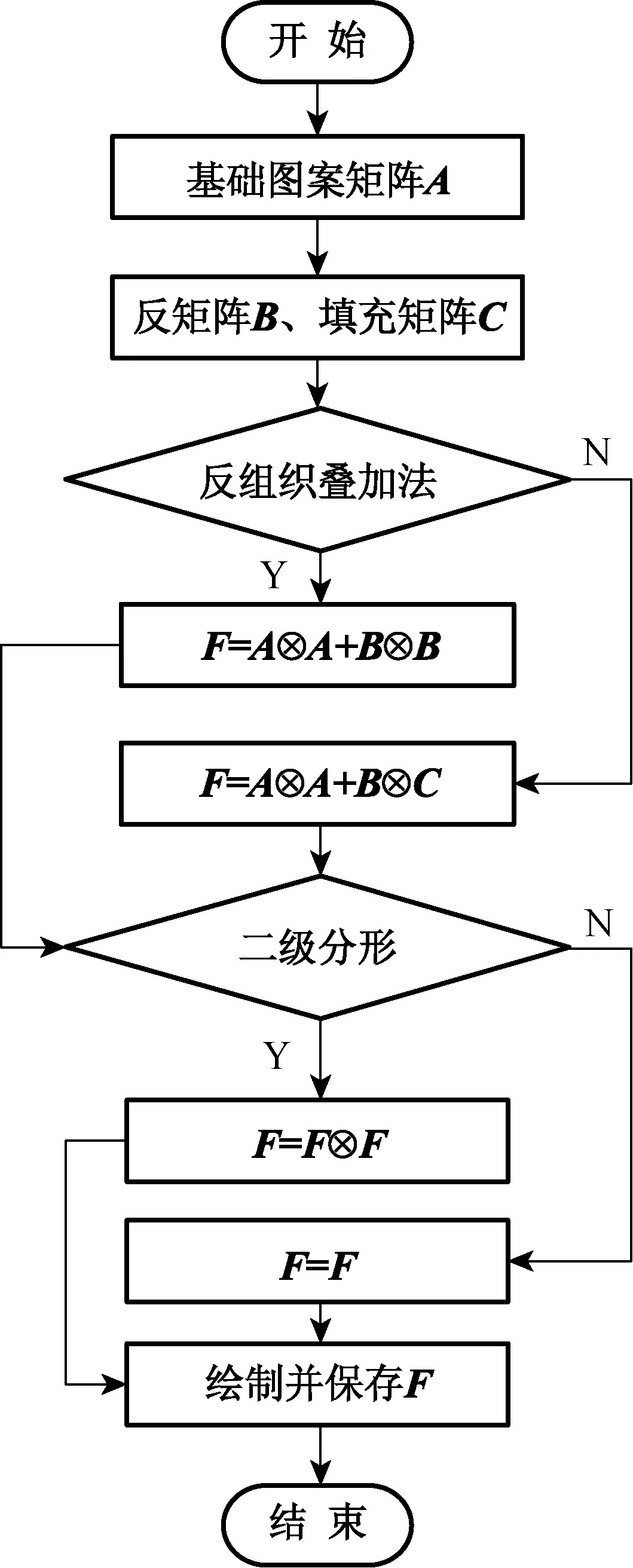
图2 分形图案矩阵生成的程序流程图Fig．2 The sketch map of program generated by a fractal pattern matrix

由图2可知，首先建立基础图案矩阵A，并生成反组织矩阵B及填充矩阵C，根据叠加生成分形组织矩阵F．如选择反组织叠加，则调用Kronecker函数计算矩阵A⊗A、B⊗B并相加得到矩阵F；如选择填充叠加，则调用Kronecker函数计算矩阵A⊗A、B⊗C，并相加得到矩阵F．如需要二级分形，则将计算F⊗F．最后，绘制并保存矩阵F．

2 基于叠加的分形图案生成方法

2．1 反组织叠加法

反组织叠加，实际上是将基础图案矩阵A和其反组织矩阵B分别进行一级分形后，进行叠加从而产生矩阵F，其计算如式(1)所示．

F=A⊗A+B⊗B

(1)

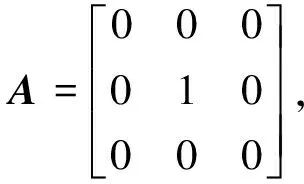
(a) 矩阵A图案 (b) 矩阵B图案 (c) A⊗A图案

(d) B⊗B图案 (e) 叠加图案 (f) 二级分形图案 图3 反组织叠加示意图Fig．3 The sketch map of inverse matrix addition

2．2 填充组织叠加法

填充组织叠加，实际上是将基础图案矩阵A进行一级分形后，再计算反组织矩阵B与填充组织C的Kronecker积，最后叠加得到矩阵F，其计算如式(2)所示.

F=A⊗A+B⊗C

(2)

根据文献[9-10]的思路，本文以斜纹组织为例，选择相应填充组织形成具有回形效果的图案，其示意图如图4所示.图4(a)、(b)分别为基础组织1、2．图4(c)、(d)分别为填充组织1、2．图4(e)、(f)为根据式(2)生成具有回纹效果的分形组织图案．

(a) 基础组织1 (b) 基础组织2 (c) 填充组织1

(d) 填充组织2 (e) 叠加组织1 (f) 叠加组织2 图4 填充组织叠加示意图Fig．4 The sketch map of filling matrix addition

3 应用实例

根据反组织及填充组织叠加法，进行具有分形效果的望江挑花图案设计(如图5所示)．图5(a)是通过反组织叠加法得到的图案．运用式(1)分别计算基础图案矩阵及反矩阵一级分形，叠加后再次进行二级分形图案，其运用于望江挑花的实物局部效果如图5(c)所示.该图案布局合理，分布匀称，既可用于挑花主体图案，也可作为局部修饰图案．图5(b)是通过填充组织叠加法得到图案．运用式(2)分别计算基础图案矩阵一级分形，再将基础图案反组织矩阵与填充组织进行Kronecker积运算，并经过叠加后的图案，其运用于望江挑花的实物局部效果如图5(d)所示，该图案呈现典型的回形纹样，较适合作为望江挑花的局部边饰．

(a) 图案1 (b) 图案2

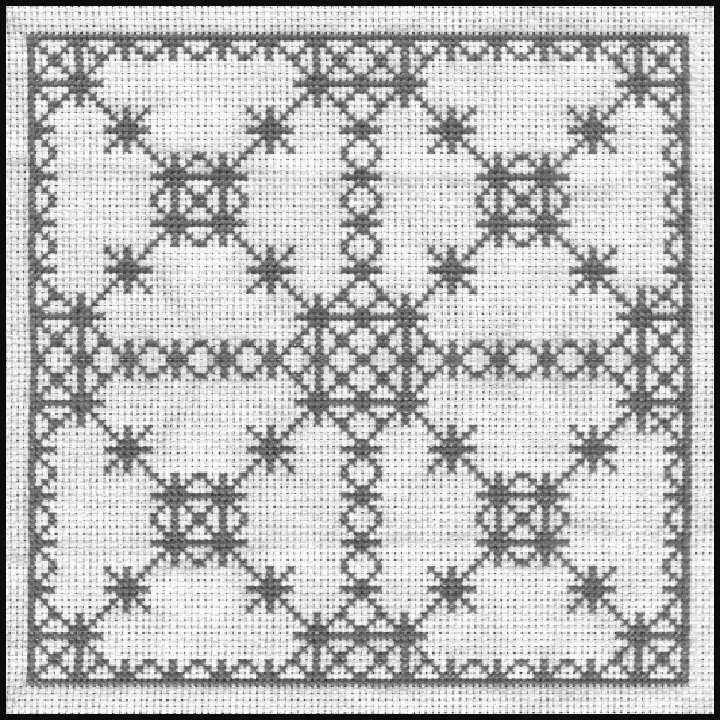
(c) 实物1 (d) 实物2 图5 望江挑花实例Fig．5 The example of Wangjiang cross stitch

4 结 语

结合分形艺术及望江挑花图案的特征，提出了基于Kronecker积的望江挑花分形图案生成方法．将基础图案矩阵、基础图案矩阵的反矩阵以及填充图案矩阵进行多级分形处理并采用叠加方式，生成分形图案矩阵．随基础图案、填充图案矩阵的不同，可设计出各具特色的分形图案，为望江挑花图案设计拓宽了新思路．

[1] 高山，王世福．望江挑花艺术的特征分析[J]．丝绸，2011，48(1)：44-47．

[2] 朱胜甲．望江挑花图案与制品的对应关系[J]．科技信息，2011，(16)：401．

[3] 顾平，丁立新．计算机生成双层组织的计算方法——Kronecker积的应用[J]．苏州丝绸工学院学报，1995，15(2/3)：28-39．

[4] 王旭，毕松梅．Kronecker积在变化绉组织设计中的应用[J]．纺织学报，2012，33(5)：40-45．

[5] 岑科军，贾静静，孙家武，等．基于L系统的3×3平纹分形组织设计应用方法[J]．纺织学报，2011，32(11)：49-52．

[6] 韩伟．Kronecker乘积生成分形图形和放大图像[J]．哈尔滨理工大学学报，2011，16(2)：49-52．

[7] 王小铭，李福清．基于分形矩阵的编织物图案设计与生成[J]．纺织学报，2003，24(4)：37-39．

[8] 袁惠芬，方妍，王旭，等．望江挑花针法形成规律研究[J]．武汉纺织大学学报，2016，29(2)：29-32．

[9] 熊丽丽，张聿．基于斜纹基本组织的回纹分形组织设计方法[J]．丝绸，2015，52(1)：31-34．

[10] 章平，张聿．同层仿射分形织物的设计方法[J]．丝绸，2014，51(12)：35-38．

FractalPatternDesignBasedonKroneckerProductandtheApplicationinWangjiangCrossStitch

YUANHuifena，CHENGWanyua，WANGXua， b，LIUXinhuaa， b

(a． College of Textile and Clothing；b． The Science and Technology Public Service Platform for Textile Industry， Anhui Polytechnic University， Wuhu 241000， China)

In order to enrich the Wangjiang cross stitch pattern design， fractal pattern generation method based on matrix Kronecker product was proposed and applied to Wangjiang cross stitch pattern design． The basic patterns’ matrix multilevel fractal processing was fulfilled by Boolean matrix model of cross stitch patterns and Kronecker product． The fractal patterns matrix was generated by multilevel matrix superimposition including basic pattern matrix， inverse basic pattern matrix and filling patterns matrix． The results show that patterns multilevel matrix fractal can be quickly realized by matrix Kronecker product． Different multilevel fractal patterns can be generated by matrix superimposition with the different basic patterns’ matrix and filling patterns’ matrix． This method expands the pattern design method of the Wangjiang cross stitch．

wangjiang cross stitch； Kronecker product； fractal； boolean matrix

1671-0444(2017)05-0651-04

2016-06-20

安徽省高校重点实验室开放基金资助项目(2015FZ001)

袁惠芬(1972—)，女，安徽巢湖人，教授，硕士，研究方向为服装CAD． E-mail： yuanhuifen @hotmail．com

TS 101．8

A

(责任编辑：杜佳)