基于观测器的不确定再入飞行器模型的控制

杨夫猛， 寇春海

(东华大学 理学院， 上海 201620)

基于观测器的不确定再入飞行器模型的控制

杨夫猛， 寇春海

(东华大学 理学院， 上海 201620)

利用Lyapunov稳定性理论并结合LMI(linear matrix inequation)方法，基于状态观测器，研究了一类含有不确定时变参数的再入飞行器模型的控制问题.首先，验证了观测器的可行性.其次，基于观测器设计了状态反馈控制器，以保证系统的稳定性.最后，给出一个再入飞行器模型的实例仿真以验证新提出的方法的有效性.

再入飞行器； 状态观测器； 控制器； 稳定性

近年来，高速再入飞行器被广泛应用于载人航天工程、探月工程等领域，因而其成为研究热点.由于在再入飞行器的再入过程中，其飞行时间变长、飞行环境不断变化和质心偏移等各种因素会影响系统的稳定性，因此对其进行相应的有效控制显得尤为重要[1-3].关于飞控系统稳定性的研究成果很多.如文献[4]基于轨迹优化，提出了一种针对含有不确定参数和外部干扰的再入飞行器模型的自适应方法，但其输入矩阵中的不确定参数不是时变矩阵.文献[5]研究了一类输入矩阵中未含不确定时变参数的系统，利用自适应方法，给出了一种自适应控制器.文献[6]在未考虑输入矩阵中含有不确定参数的情况下，设计滑模面，给出了一种自适应滑模控制器，保证闭环系统的全局稳定.文献[7]研究了一类系统矩阵中未含有不确定参数的飞控系统，利用滑模跟踪控制方法，设计一个跟踪控制器以抑制系统的不稳定现象.在实际飞控系统中，不确定因素的存在会对系统建模及控制输入带来影响，因此有必要在系统矩阵和输入矩阵中同时加以考虑不确定因素.在设计控制器时，文献[4-5]假设所有状态信号均可获取，但是实际系统的状态并非如此，有些状态根本无法有效得到，这对控制器的设计带来诸多不确定因素.为了估计未知状态，文献[8-9]基于状态观测器，采用LMI(linear matrix inequation)方法，设计了状态反馈控制器，以控制系统稳定，但是其中的观测器和控制器没有分开设计，不能更好地验证各自的有效性能.

基于以上分析，本文研究了一类不确定再入飞行器模型，其系统矩阵和输入矩阵中同时含有不确定时变参数.利用Lyapunov稳定性理论并结合LMI方法提出了一种基于观测器的控制方法，其中观测器和控制器分别单独进行设计，通过验证各自的可行性，给出了保证系统稳定的充分条件.

1 问题描述

本节首先给出文中所要研究的再入飞行器模型和含有不确定时变参数的再入飞行器模型.

1.1 再入飞行器模型

文献[4]研究的再入飞行器系统方程如下所示.

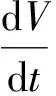
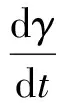
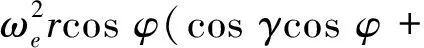
sinγsinφcosψ)，

2ωeV(tanγcosψcosφ-sinφ)+

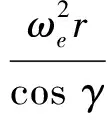
q=0.5ρ1V2，ρ1=ρ0e-ζ h，g=g0(R/(R+Rh))2，

式中：m，V分别为飞行器的质量和速度；ωx，ωy，ωz分别为机体x轴，y轴，z轴的角速度；T，FT，FN为机体轴对质心的空气动力；Mx，My，Mz分别为x轴，y轴，z轴的力矩；γ，ψ分别为航迹角和航向角；R为地球半径；θ，φ分别为经度和纬度；ξ为再入飞行器的倾斜角；Ix，Iy，Iz，Ixy，Iyz，Izx表示机体轴的转动惯量；r为质心相对于地心的高度；q为动态压力；ρ1为大气密度；ρ0为海平面大气层密度；x，z为横、侧向的距离；CD，CL分别为阻力、升力系数；S为飞行器参考面积；ωe，g0分别为地球角速度和重力加速度；ζ，h分别为密度系数和海拔高度.

经过一阶线性化后，上述方程可表示为如式(1)的矩阵形式.

(1)

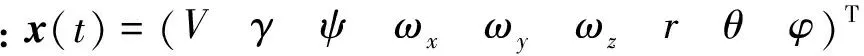
1.2 不确定再入飞行器模型

在再入飞行器的再入过程中，系统会受到不确定因素的影响而发生变化，系统稳定性也会受到影响.本文为考虑含有不确定时变参数的再入飞行器模型.

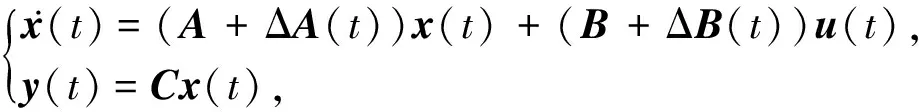
(2)

式中：x(t)∈Rn为状态向量；u(t)∈Rm为控制向量；y(t)∈Rp为输出向量；A，B分别为系统矩阵和输入矩阵；C为已知矩阵；ΔA(t)， ΔB(t)是不确定矩阵，满足

(3)

式中：Mi，Ni为已知矩阵；I为单位矩阵.且假设系统(A，C)可观测，系统(A，B)可控.

2 观测器设计和基于观测器的控制器设计

在实际飞控系统中，系统状态并非能全部直接得到，仅有输出变量可以直接得到.本节主要借助状态观测器以估计实际状态，并基于观测器设计状态反馈控制器.在设计观测器和控制器之前，首先给出以下定义和引理.

引理2[10](Schur补引理)对于给定的实对称矩阵

式中：S11为r×r维.下列条件等价：

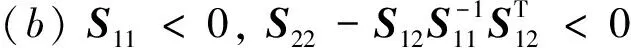
引理3[11](Young不等式)对于∀η>0及实向量x和y，有下面不等式成立：

2xTy≤ηxTx+η-1yTy.

(4)

2.1 观测器设计

由于实际系统中的状态变量并非能全部直接获取，为了估计未知的实际状态，根据系统(2)，设计状态观测器

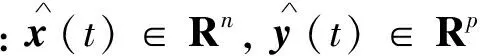
定义

式中：e(t)∈Rn为状态估计误差向量，则状态估计误差动态方程为

(5)

定理1若存在μ>0，正定矩阵P∈Rn×n和矩阵L∈Rn×p满足

(6)

则状态估计误差动态系统(5)是稳定的，其中Φ11=(A-LC)TP+P(A-LC).

证明选取Lyapunov函数

V1(e)=eTPe，e∈Rn.

则它沿着式(5)的解的导数为

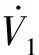
eT(t)((A-LC)TP+P(A-LC))e(t)+2eT(t)PΔA(t)e(t)，

(7)

由式(3)和(4)可知，存在μ>0使得

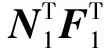
(8)

将式(8)代入式(7)中，得

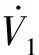
由引理2知，式(6)等价于

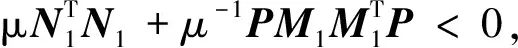
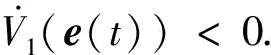
2.2 控制器设计

基于上述设计的观测器，设计系统(2)的状态反馈控制器，并给出使系统(2)稳定的充分条件.

基于状态观测器，设计如下状态反馈控制器

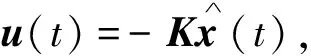
(9)

式中：K∈Rm×n为待确定的反馈增益矩阵.

在给出主要结果之前，首先给出一个引理.

引理4[12]假设系统(A，B)可控，则存在反馈增益矩阵K∈Rm×n使得A-BK稳定，即A-BK为Hurwitz矩阵.

定理2若存在εi>0(i=1， 2， 3， 4)，正定矩阵H∈Rn×n和矩阵K∈Rm×n，使得

(10)

式中：

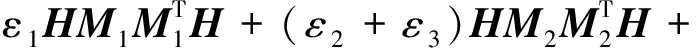
Π12=HBK，

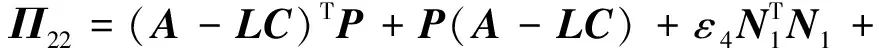
式中：K为式(9)中的反馈增益矩阵.则控制器(9)可使系统(2)稳定.

证明将控制器(9)代入系统(2)中，则系统(2)可写为

(A-BK)x(t)+(ΔA(t)-

ΔB(t)K)x(t)+(B+ΔB(t))Ke(t).

(11)

考虑Lyapunov函数

V2(x，e)=xTHx+eTPe，x，e∈Rn.

则它沿着式(11)的解的导数为

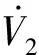
xT(t)((A-BK)TH+H(A-BK))x(t)+ 2xT(t)HΔA(t)x(t)- 2xT(t)HΔB(t)Kx(t)+ 2xT(t)HBKe(t)+ 2xT(t)HΔB(t)Ke(t)+

eT(t)((A-LC)TP+P(A-LC))e(t)+ 2eT(t)PΔA(t)e(t)，

(12)

式中：正定矩阵P∈Rn×n和矩阵L∈Rn×p由定理1给出.

又由式(3)和(4)知，存在εi>0(i=1， 2， 3， 4)分别满足

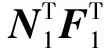
(13)

将式(13)代入(12)中得

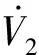
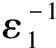
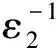
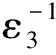
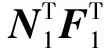
xT(t)((A-BK)TH+H(A-BK))x(t)+

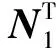
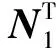
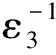
然而，要找到满足上述条件的H和K并不容易，下面结合LMI方法给出定理2的一个推论以求解反馈增益矩阵K.

推论假设正定矩阵P∈Rn×n和矩阵L∈Rn×p满足定理1条件，若存在εi>0(i=1， 2， 3， 4)和矩阵K∈Rm×n，使得

(14)

式中：

E11=AT+A-KTBT-BK+

则基于观测器的控制器(9)使系统(2)稳定.

此推论说明，若求解式(14)求出矩阵K，则基于观测器的控制器便可得到.

3 实例仿真

下面给出实例仿真，以验证上述设计的有效性.

在系统(2)中，分别取矩阵A，B，C如下[4]：

不确定矩阵(3)中的M1，M2，F1(t)，F2(t)，N1，N2及系统(2)的初始向量分别取为

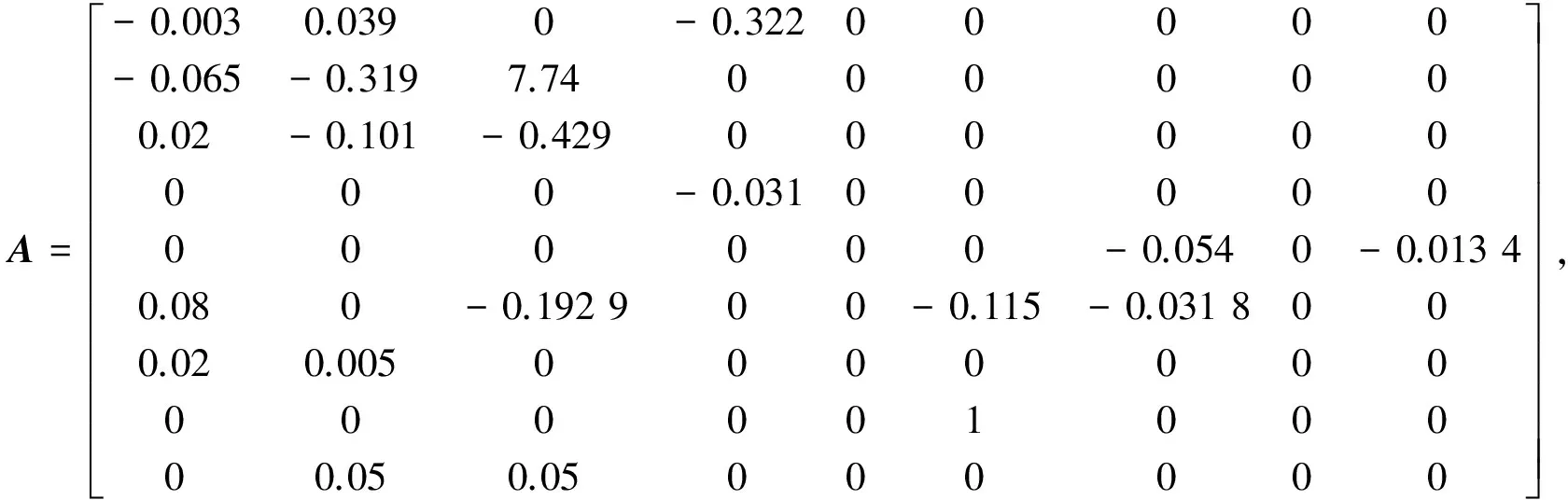
并选取参数μ=18，ε1=10-2，ε2=10-3，ε3=103，ε4=102.系统仿真结果如图1和2所示.

(a) 攻角偏转度 (b) 偏航角偏转度 (c) 倾斜角偏转度

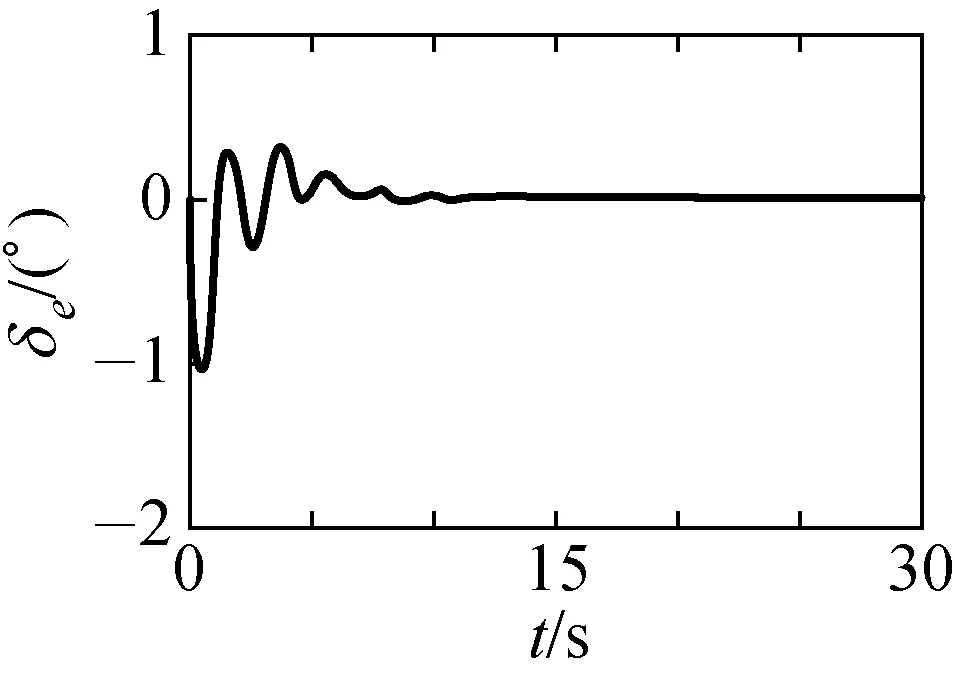
(d) 升降舵偏转度 (e) 副翼偏转度 (f) 方向舵偏转度 图1 控制输入信号Fig.1 Control input signals

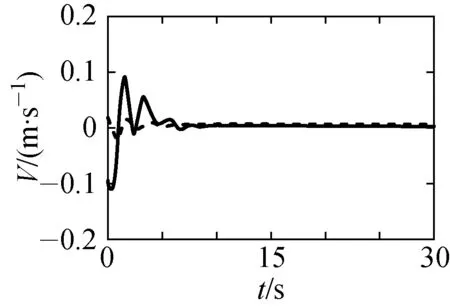
(a) 速度 (b) 航迹角 (c) 航向角

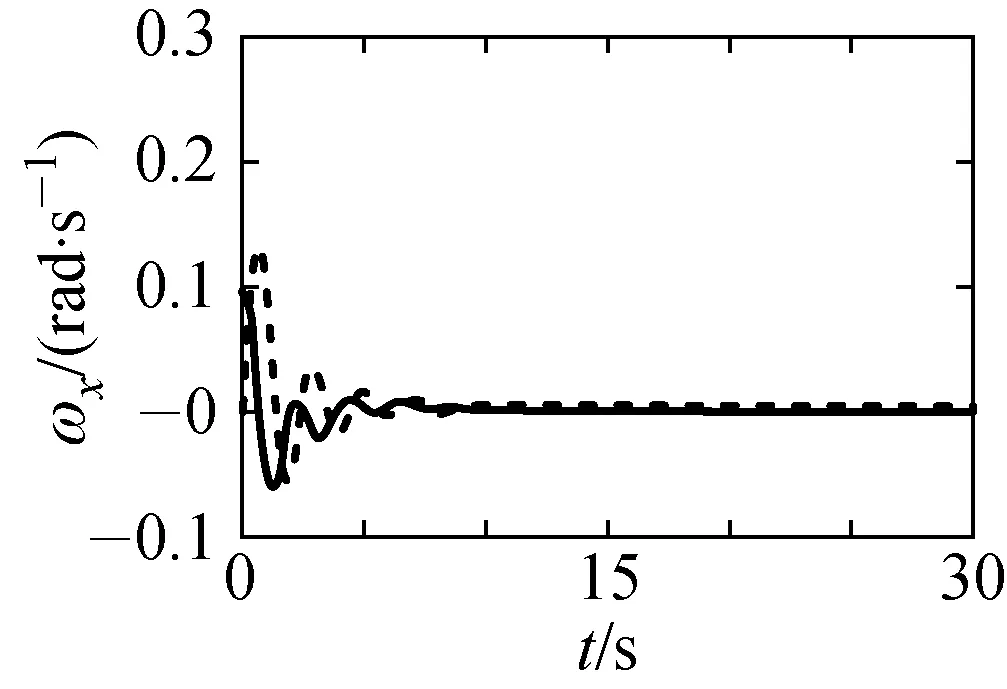
(d) x轴角速度 (e) y轴角速度 (f) z轴角速度

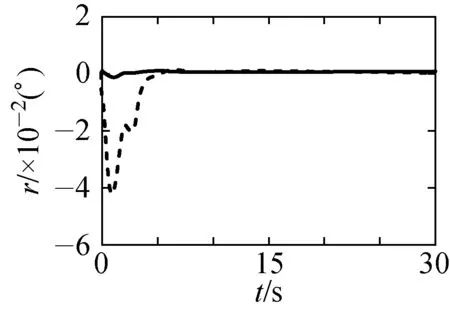
(g) 质心高度 (h) 经度 (i) 纬度 图2 实际状态(实线)与估计状态(虚线)轨迹Fig.2 Trajectory of the actual states (solid line) and the estimated states(dotted line)

图1是系统在受到不确定因素影响时(0时刻开始)，对系统输入的控制信号；图2是再入飞行器的实际状态(实线)与状态观测器所观测的状态(虚线)的轨迹.从图1和2中可以清晰看出，所设计的观测器能够很好地观测再入飞行器系统的实际状态，通过反馈控制器，将所观测到的状态代入到实际系统中，并在短时间内有效地使系统达到了稳定状态.

4 结 语

本文研究了一类含有不确定时变参数的再入飞行器模型的控制问题，主要利用Lyapunov稳定性理论和LMI(Linear Matrix Inequation)方法，分别单独设计了状态观测器和状态反馈控制器，最后通过实例仿真验证了所提方法的有效性.

[1] BORGLUND D， KUTTENKEULER J. Active wing flutter suppression using a trailing-edge flap[J]. Journal of Fluids and Structures， 2002， 16 (3)： 271-294.

[2] HAN J H， TANI J， QIU J H. Active flutter suppression of a lifting surface using piezoelectric actuation and modern control theory[J]. Journal of Sound and Vibration， 2006， 291 (3/5)： 706-722.

[3] GIBSON T E， CRESPO L G， ANNASWAMY A M. Adaptive control of hypersonic vehicles in the presence of modeling uncertainties[C]//American Control Conference. St Louis， MO， USA： Institute of Electrical and Electronics Engineers， 2009： 3178-3183.

[4] GAO M Z， CAI G P， NAN Y. Adaptive fault-tolerant control of reentry vehicle considering actuator and sensor faults based on trajectory optimization[J]. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2016， 230 (4)： 726-746.

[5] WANG J， PEI H L， WANG N Z. Adaptive output feedback control using fault compensation and fault estimation for linear system with actuator failure[J]. International Journal of Automation and Computing， 2013， 10(5)： 463-471.

[6] HU X X， WU L G， HU C H， et al. Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J]. Journal of the Franklin Institute， 2012， 349 (2)： 559-577.

[7] JIN X Z， YANG G H， ChANG X H. Robust H∞and adaptive tracking control against actuator faults with a linearised aircraft application[J]. International Journal of Systems Science， 2013， 44 (1)： 151-165.

[8] 丁明芳，徐跃良，吴莉华.一类不确定线性系统的基于观测器的鲁棒控制器设计[J].四川理工学院学报(自然科学版)，2008，21(1)：22-24.

[9] LIEN C H. Robust observer-based control of systems with state perturbations via LMI approach[J]. IEEE Transaction on Automatie Control， 2004， 49(8)： 1365-1370.

[10] 廖晓昕.稳定性的理论、方法和应用[M].2版.武汉：华中科技大学出版社，2010.

[11] 俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京：清华大学出版社，2002.

[12] 郑大钟.线性系统理论[M].2版.北京：清华大学出版社，2002.

Observer-BasedControlfortheReentryVehicleModelwithUncertainty

YANGFumeng，KOUChunhai

(College of Science，Donghua University， Shanghai 201620， China)

Based on state observer，the control for a class of reentry vehicle model with uncertain invariant parameters is discussed by using the Lyapunov stability theory together with the LMI (linear matrix inequation) opproach. Firstly，the feasibility of the observer is verified. Then， an observer-based state feedback controller is designed， which guarantees the stability of the related systems. Finally， a numerical simulation for a reentry vehicle model is presented to illustrate the effectiveness of the new proposed design methods.

reentry vehicle； state observer； controller； stability

1671-0444(2017)05-0764-07

2016-06-25

中央高校基本科研业务费专项基金资助项目(CUSF-DH-D-2014061)

杨夫猛(1987—)，男，山东滕州人，硕士研究生，研究方向为常微分方程.E-mail： yfmclp@163.com

寇春海(联系人)，男，教授，E-mail： kouchunhai@dhu.edu.cn

O 231.1

A

(责任编辑：杜佳)